北部湾海浪季节变化和驱动因素的数值模拟研究

赵红军，王俊达，孔俊，陈国平

( 1. 河海大学 港口海岸与近海工程学院，江苏 南京 210098；2. 河海大学 海岸灾害及防护教育部重点实验室，江苏 南京 210098)

1 引言

北部湾是“海上丝路”的主要海湾，是中国西南地区的出海门户，位于南海西北部，东临雷州半岛和海南岛，北靠广西，西依越南，战略位置重要，渔业和油气资源丰富。波浪不仅是影响海洋运输、渔业捕捞、油气开采等各种海上活动作业安全的主要因素，也是诱发海岸和海洋灾害、威胁工程结构安全的重要动力因子，传播至近岸的波浪还会诱导近岸环流，影响海岸泥沙运动和塑造海岸地貌形态[1]。为保障北部湾各类海上活动和基础设施建设，需要对湾内海浪的时空分布和影响因素开展深入研究。

长时间连续的海浪参数（如波高、波周期、波向等）是进行海浪时空分布研究的基础，由于现场观测资料和卫星遥感资料的时长和时空分辨率有限，数值模拟成为了获取海浪参数的重要手段。目前常用于海浪模拟的数值模型主要有WAM[2]、WWⅢ[3]、SWAN[4]等。不同于WAM和WWⅢ更适用于深水洋区，SWAN由于合理计及了浅水域中的各种能量源项，尤其适用于近岸，并且因为丰富了深水能量源项和引入了高阶计算格式，还可在大洋尺度应用[5]。在海浪模拟中，海面风是驱动海浪模型开展数值模拟的关键，因为风不仅控制着局地风能输入，风浪还会传离风区影响远域，所以海浪的模拟效果在很大程度上依赖于风场。目前常用于全球/区域海洋波浪后报的再分析风资料有CFSR[6]、CFSV2[7]、ERA-Interim[8]等，其中，CFSR[6]由美国国家海洋和大气管理局（NOAA）国家环境预报中心（NCEP）发布，资料时限为1979-2011年，时间分辨率为1 h，空间分辨率约为0.3°；作为CFSR的升级延续，CFSV2[7]再分析数据始自2011年，空间分辨率约为0.2°；ERA-Interim[8]由欧洲中期天气预报中心（ECMWF）发布，时限为1979-2019年，时间分辨率为3 h，空间分辨率约为0.7°。文献[9]使用卫星和浮标资料评估了CFSR和ERA-Interim的风速质量，尽管两项数据的误差水平相当，但CFSR风场对海浪的模拟效果却略优于ERA-Interim。文献[10]利用多个海洋浮标站测风资料对CFSV2和ERA-Interim风场在中国沿海的适用性进行了分析，结果显示，二者风向误差相差不大，但CFSV2的风速误差却略小于ERAInterim。利用CFSR/CFSV2风场驱动海浪模型，文献[11-12]分别对全球和中国近海开展了长时间连续海浪过程的数值后报，取得了良好的模拟效果。

近年来为顺应波候、极值波浪要素、波浪能评估等的需要，已有研究针对中国沿海[12]、黄海和渤海[13-14]、东海[15]、南海[16-17]、北部湾[18]等海域的多年海浪过程进行了数值模拟。其中，文献[16-17]在模拟南海海浪时，尽管模拟范围覆盖了北部湾，但模型的空间分辨率相对较低，这对北部湾海浪模拟效果有何影响未有定量评估。文献[18]利用SWAN和ERAInterim风场针对北部湾多年海浪进行了后报，但模拟时未考虑南海传入北部湾的海浪。利用ERA-Interim波浪资料，文献[19-20]分别分析了南海和北部湾海域有效波高的年、季变化特点，基础资料的空间分辨率同样存在相对较低的不足。北部湾夏季6-8月盛行西南季风，并有台风影响；冬季11月至翌年2月盛行东北季风，稳定少变；3-5月和9-10月分别是冬夏和夏冬季风转换期。在季风控制下，湾内海浪的强度和方向均具有显著的季节变化[18,20-21]。北部湾与南海相连，南海传入浪亦会影响海湾的波浪场[20]。作为驱动因素，关于局地风和南海传入浪对北部湾波浪的影响缺乏系统认识。为此，本文针对北部湾，利用CFSV2风场驱动SWAN模型，对整年海浪过程进行了数值模拟，在检验模型应用效果、评估空间网格尺度对模拟结果影响的同时，还分析了北部湾波浪的季节变化特点，讨论了局地风和传入浪的驱动贡献。

2 数值模型

2.1 SWAN模型

SWAN是荷兰Delft理工大学基于波作用量守恒方程开发的第三代海浪数值模型[4]，该模型采用隐式格式离散控制方程，较WAM和WWⅢ，更为全面地考虑了浅水波浪的传播变形过程。在球坐标系下模型的控制方程可表达为

式中，N为波作用量密度；Cλ和Cφ分别为波浪在地理空间（纬度空间λ和经度空间φ）的传播速度；Cσ和Cθ分别为波浪在谱空间（频率空间σ和方向空间θ）的传播速度；S为源函数项，可表示为

式中，Sin为风能输入项；Sds为能量耗散项，包括白浪破碎耗散、海底摩擦耗散、植被耗散、水深诱导的波浪破碎耗散等；Snl为非线性波波相互作用项，包括深水四波相互作用和浅水三波相互作用。

2.2 模型参数设置

北部湾地处南海西北部，北面和西面被广西和越南包围，东面被雷州半岛和海南岛掩护，并通过琼州海峡与南海相连。为反映北部湾水陆形势变化，同时兼顾计算效率，采用南海波浪模型和北部湾波浪模型嵌套计算的方案。两个模型均采用球坐标系，其中：南海模型范围为4°S～26°N，99°～129°E，向北包括台湾岛，南抵加里曼丹岛，向东涵盖吕宋海峡（图1a），空间分辨率为12′×12′；北部湾模型范围为17°～22°N，105.5°～112.5°E，包括海南岛、雷州半岛和粤西沿海（图1b），空间分辨率为2′×2′；数值模型的水深由NOAA国家地球物理数据中心（NGDC）开发的ETOPO1全球地形数据生成，空间分辨率为1′×1′。在二维波谱空间上，频率的模拟范围为0.033～1.0 Hz，以对数分布划分为30个；方向分辨率为10°，均匀划分为36个。

模型驱动风场由NOAA NCEP 开发的CFSV2海面10 m风速数据[7]提供，资料的空间分辨率为0.205°×0.205°，时间分辨率为1 h。在入射波浪边界条件的设置上：鉴于南海被系列岛屿环抱而相对封闭，所以南海波浪的模拟不考虑西北太平洋传入浪的影响；北部湾模型的入射波边界以二维波谱的方式由南海模型逐时提供。在海浪模拟的物理机制上：风能输入考虑线性增长和指数增长两部分，其中线性增长采用Caraler和Malanotte-Rizzoli[22]公式；指数成长采用Komen等[23]的表达式；白浪损耗采用Komen等[23]的研究成果；四波非线性相互作用采用Hasselmann等[24]离散迭代近似模型；模型可调参数取默认值[25]；海底摩阻损耗采用Collins[26]公式，海底摩阻因数取0.01；不考虑水流作用和水位变化对波浪传播变形的影响，已有研究显示：在北部湾，波流相互作用引起的有效波高变化不超过30%[27]。文中的模拟还改变了对北部湾模型驱动风场和入射边界条件的设置，设计了不同的模拟工况，以辨析局地风和南海传入浪对北部湾波浪场的影响。

图1 南海波浪模型（a）和北部湾波浪模型（b）的模拟范围Fig. 1 Simulation range of the South China Sea wave model (a) and the Beibu Gulf wave model (b)

模型模拟的时间范围为2011年8月至2012年7月；考虑到单机计算的时耗，模拟采用冷启动的方式逐月开展，各月均向前模拟5 d，以消除冷启动对模拟结果的影响。模型输出变量包括有效波高Hs、平均波周期Tm、谱峰波周期Tp和平均波向Dir，输出变量的时间分辨率为1 h，空间分辨率与模型计算网格一致。

3 模拟结果检验

3.1 基于Jason-2卫星有效波高数据的检验

为评估模型在深水域的模拟效果，并检验南海模型为北部湾模型提供入射波边界的合理性，收集了Jason-2卫星高度计的有效波高数据。在2011年8月至2012年7月，Jason-2卫星在南海北部海域（12°～23°N，105°～123°E）共有592条轨道数据生成，轨道路径见图1a。鉴于在卫星升轨道和降轨道的交叉点上，观测数据具有更高的时间分辨率（年内的时序数据约为70个），同时考虑到分区域检验的需要，选取轨道交叉点A1-A4、B1-B4和C1-C4（图1a）的有效波高时间系列数据进行模型模拟效果的评估。图2给出了交叉点有效波高模型模拟值与卫星观测值的散点分布；表1对模拟值和观测值进行了定量比较，包括平均误差（MB）、均方根误差（RMSB）和分散系数（SI），计算公式分别为

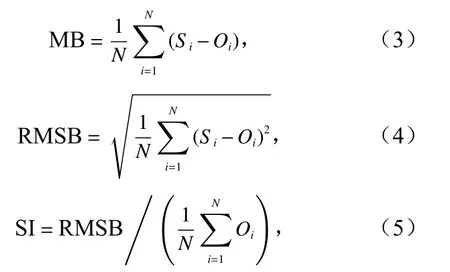
式中，Si和Oi分别代表模拟值和观测值；N是样本数。

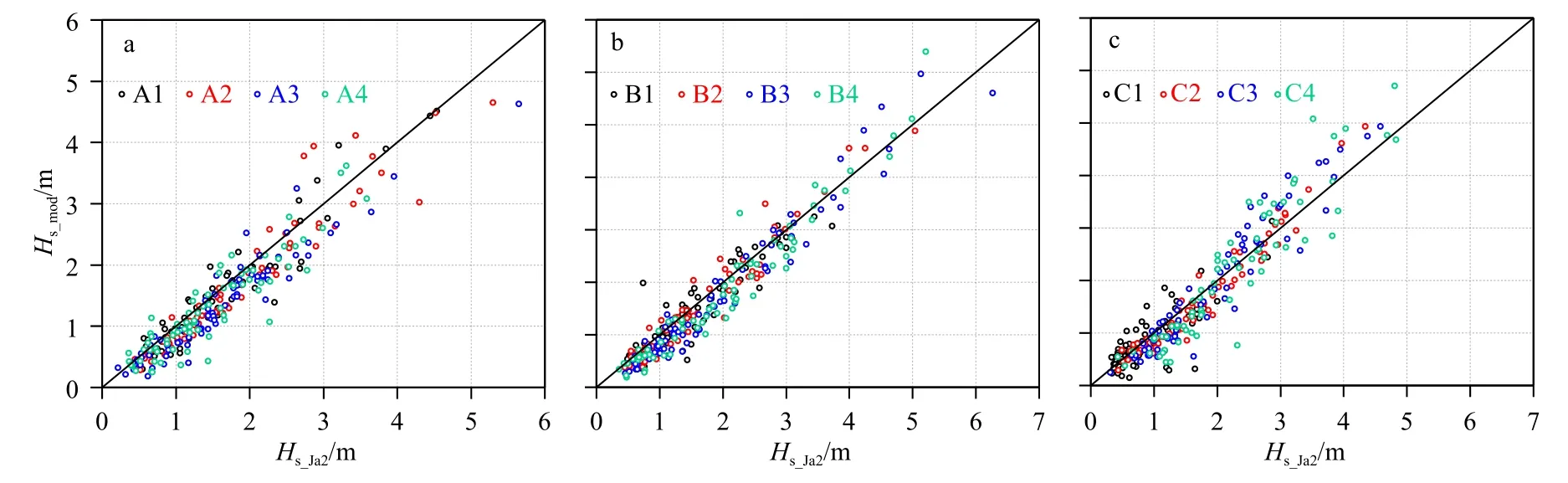
图2 有效波高模拟值Hs_mod与Jason-2卫星观测值Hs_Ja2的散点分布Fig. 2 Scatter diagrams for the results of significant wave height between model simulations Hs_modand Jason-2 satellite observations Hs_Ja2

总体上看，有效波高模拟值较卫星观测值略低，尤其是在平常期有效波高小于2 m时更为明显（图2a至图2c）；在21°N附近C系列点，模拟值较卫星数据的平均误差在-0.09～0.01 m，优于13°N附近的A系列点（平均误差为-0.26～-0.11 m），B系列点的平均误差值介于A系列点和C系列点之间。文献[12, 17]在利用海洋站/浮标观测资料检验各自模型的模拟效果时，亦存在有效波高模拟结果偏小的现象。有效波高模拟值较卫星观测数据偏小可能与CFSV2风速在中国沿海偏弱有关，文献[10]评估显示，CFSV2风速值略小于沿海浮标观测值，二者平均误差为-0.55 m/s。此外，从模拟结果较卫星数据的分散程度上看，除C1点因地处近岸，波浪传播变形的影响因素多而致使分散系数（0.35）相对较大外，其他深水点的分散系数多为0.2左右；尤其是位于北部湾模型入射边界附近的B1点和B2点，有效波高模拟值的平均误差、均方根误差和分散系数分别约为-0.1 m、0.3 m和0.2，这说明了北部湾海浪模型入射波浪边界的合理性。

3.2 基于近岸浮标整年波浪观测数据的检验

2011年8月至2012年7月，在广西白龙半岛南部约3 km的近岸投放了波浪浮标，进行了历时1年的逐时波浪观测，观测点BL的地理位置见图1b，水深变化在10～13 m，资料完整率为99.9%。为检验模型对近岸波浪的模拟效果，图3a至图3c分别对观测点处有效波高、平均波周期和平均波向（按来向自正北顺时起算）的逐时模拟值与观测值进行了过程比较；表2对模型模拟值较浮标观测值进行了详细的误差统计分析，包括平均值、最大值、平均误差、均方根误差和分散系数，表中统计按风期进行：夏季风期为6-8月、夏冬转换季为9-10月、冬季风期为11月至翌年2月、冬夏转换季为3-5月。

白龙浮标地处北部湾顶白龙尾南部近岸，夏季西南季风控制下盛行S向浪，冬季东北季风影响下优势浪为E-ENE向（图3c），尽管夏季风的强度不及冬季风的，但因为观测站南面北部湾开敞，对岸风区长，所以夏季浪的有效波高（图3a）和平均波周期（图3b）明显强于冬季，浮标观测资料和数值模拟结果一致地反映了上述季节变化。据表2统计可知：（1）对平均波周期的模拟效果略优于有效波高，平均波周期的分散系数为0.18～0.31，有效波高的分散系数在0.37～0.44；（2）对季风期海浪的模拟效果略优于季风转换期，其中冬季风期和夏季风期大体相当，优于冬夏季风和夏冬季风转化期，有效波高和平均波周期的分散系数在季风期为0.19～0.37，在季风转换期为0.18～0.44；（3）对冬夏季风转换期的模拟效果为最差（有效波高和平均波周期的分散系数分别为0.43和0.31），模拟值较实测值略偏大（平均误差分别为0.04 m和0.42 s），平均波向的模拟误差亦为全年最大（均方根误差为32°），这可能与驱动风场在冬夏季风转换期的风向误差大有关，文献[10]研究显示，在中国沿海CFSV2风向的均方根误差在4-5月为全年最大（约50°）；（4）对极值大浪的模拟略偏小，全年最大波浪由201117号台风“纳沙”所致，台风影响期间最大有效波高和对应平均波周期的模拟值分别为3.03 m和5.72 s，略小于浮标观测值3.30 m和6.32 s，模拟波向和观测波向一致，均为SE向，台风大浪的模拟结果偏小可能是由驱动风场对台风大风风速低估导致的[28]。

3.3 空间分辨率对模拟结果的影响

已有研究[16-18,20]针对北部湾海浪进行的模拟后报和统计分析多基于0.1°～0.2°的空间网格分辨率进行，为评估空间网格分辨率对北部湾海浪模拟结果的影响，我们将南海模型模拟值（Si）和北部湾模型模拟值（Bi）进行了比较，计算了前者较后者的均方根偏差（RMSB）和平均相对偏差（MRAB），MRAB计算公式为

图3 近岸浮标BL站点有效波高Hs（a）、平均波周期Tm（b）和平均波向Dir（c）的时间变化过程Fig. 3 Time series of significant wave height Hs(a), mean wave period Tm(b) and mean wave direction Dir(c)at the nearshore buoy Point BL

表2 近岸浮标BL站点有效波高Hs、平均波周期Tm和平均波向Dir模拟值较观测值的统计比较Table 2 Statistics and comparisons for the results of significant wave height Hs, mean wave period Tmand mean wave direction Dirbetween numerical simulations and in-situobservations at the nearshore buoy Point BL

图4a至图4f显示了南海模型相对于北部湾模型有效波高模拟值的均方根偏差和平均相对偏差的空间分布和月变化情况。粗网格模型（12′×12′）模拟值较细网格模型（2′×2′）的偏差在开敞20 m以深水域较小，二者的均方根偏差一般不超过0.1 m，平均相对偏差在10%以下。因难以解译岸线变化和水下地形分布，粗网格模型的偏差向岸逐渐明显，平均相对偏差普遍在20%以上，局部如北部湾顶浅水域、琼州海峡等的平均相对偏差甚至高达80%以上。由于盛行风向不同，粗网格模型的偏差亦随季节而变化，如在北部湾口海南岛西南海域和北部湾顶浅水域，东北季风期的偏差（图4b，图4e）明显强于西南季风期的偏差（图4a，图4d），这均与粗网格模型和细网格模型关于上风向岸线和水下地形解译差异有关。由上述比较可知：空间网格分辨率约为0.2°的海浪模型可对北部湾20 m以深开敞海域进行有效计算；细化模型的空间网格分辨率有助于近岸浅水域和琼州海峡区海浪传播变形的模拟。

图4 南海模型有效波高模拟值较北部湾模型的均方根偏差（RMSB）（a-c）和平均相对偏差（MRAB）（d-f）的分布Fig. 4 Distributions of RMSB (a-c) and MRAB (d-f) of significant wave height simulated by the South China Sea model compared with the Beibu Gulf model

4 模拟结果分析

4.1 北部湾海浪的季节变化

图5a至图5l分别给出了南海月平均的有效波高、平均波向、谱峰波周期和风速分布，可见在东亚季风影响下，南海平常期海浪的强度和方向具有显著的季节变化。在11月至翌年2月冬季风期，南海盛行东北向浪，12月最强（图5a），11月次之（图略）；因为东北季风在南海东北部吕宋海峡和台湾海峡最强，向西南逐渐减弱（图5i），所以东北向季风浪有效波高的空间分布亦总体自东北向西南减弱（图5a），在吕宋海峡以西、台湾岛西南海域形成强波浪区，12月的月均有效波高可达3.6 m以上。在6-8月夏季风期，南海盛行偏西南向浪，6月最强（图5c），有效波高自西南向东北逐渐增加，夏季风期同样在台湾岛西南海域形成强波浪区，6月的月均有效波高可达2.0 m以上；由于西南季风风速（图5k）弱于东北季风风速（图5i），夏季波浪有效波高（图5c）的强度明显不及冬季波浪（图5a）。不同于有效波高，东北向季风波浪的谱峰波周期自东北向西南逐渐增大（图5e），西南季风波浪的谱峰波周期自西南向东北逐渐增强（图5g），这是涌浪传入下风向海域使然。3-5月为冬夏季风转换期，南海盛行浪向由东北转为东南（图5b）；9-10月为夏冬季风转换期，盛行浪向由西南转为东南（图5d）。

图6a至图6h分别给出了北部湾月平均有效波高、平均波向和谱峰波周期的分布。在冬季风期，北部湾盛行东北向浪，由于被雷州半岛和海南岛掩护，湾内风速（图5i）、有效波高（图6a）和谱峰波周期（图6e）均明显不及海南岛东部海域；在北部湾内，有效波高自东北向西南逐渐增强，谱峰波周期亦自东北向西南逐渐增大，这是湾内风生波浪主导所致；在北部湾口、海南岛西南海域，尽管海南岛的遮拦使局地风速明显弱于北部湾中部，但东北向季风浪却以湾口为最强，2.0 m有效波高等值线呈“舌状”自湾口伸向湾内，这与南海波浪的传入有关。在夏季风期，北部湾盛行南向波浪（图6c），波浪的空间分布表现为湾口强于湾内、东北强于西南；因为夏季风风速（图5k）不及冬季风风速（图5i）强盛，所以除湾顶近岸外，夏季波浪有效波高（图6c）明显小于冬季波浪有效波高（图6a），在广西近岸和雷州半岛西岸，水陆形势的限制使夏季浪的强度强于冬季。在季风转换期（图6b，图6d），北部湾盛行东南向浪；由于风速相对较弱，波浪强度不及季风期，且强度的空间分布总体呈现为湾口强于湾内、西南强于东北。

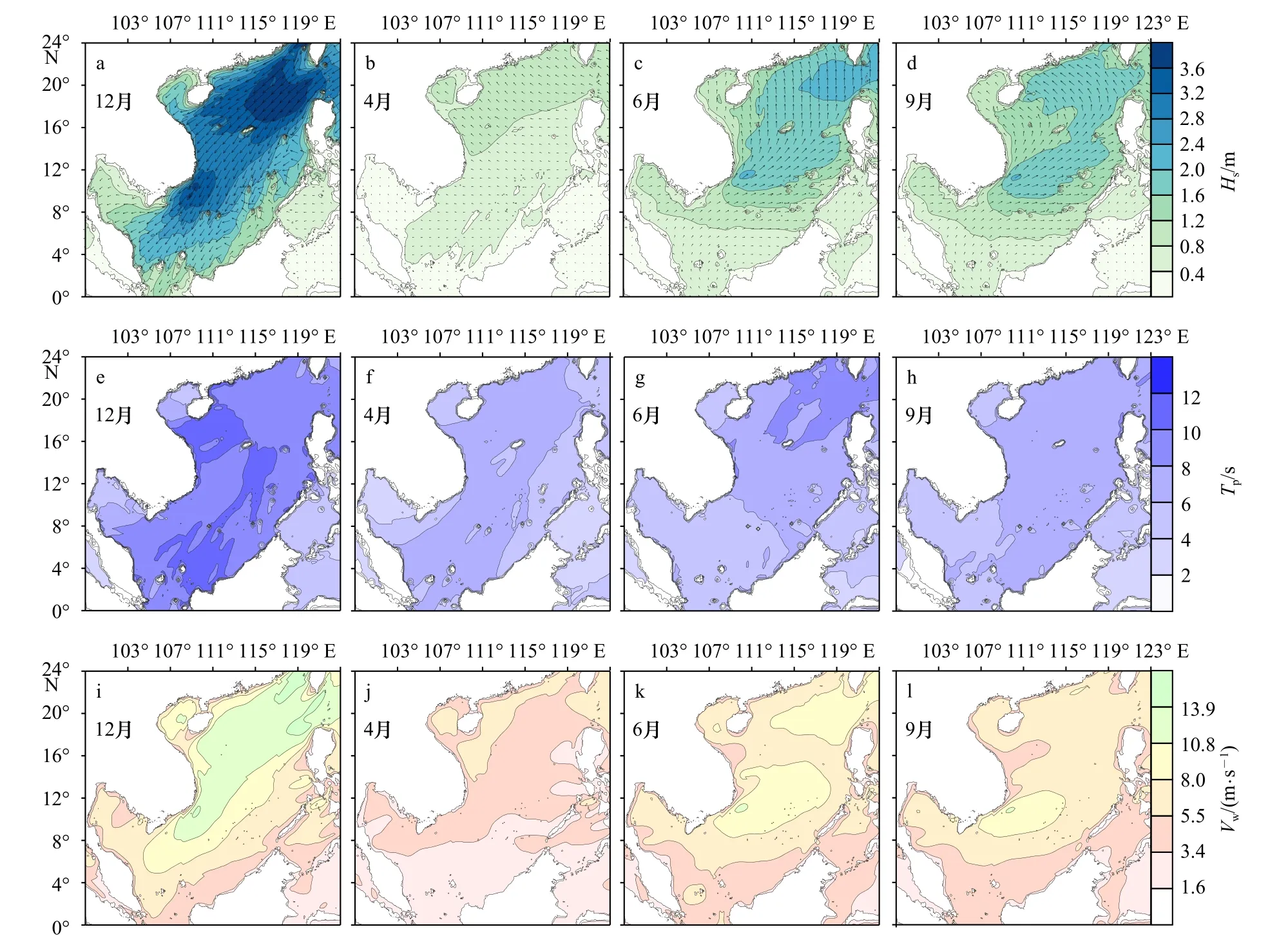
图5 南海各月平均有效波高Hs和平均波向Dir（a-d）、谱峰周期Tp（e-h）以及风速Vw（i-l）的分布Fig. 5 Distributions of month averaged significant wave height Hsand mean wave direction Dir(a-d), spectral peak period Tp(e-h) and wind speed Vw(i-l) in the South China Sea

图6 北部湾各月平均有效波高Hs和平均波向Dir（a-d）以及谱峰周期Tp（e-h）的分布Fig. 6 Distributions of month averaged significant wave height Hsand mean wave direction Dir(a-d), and spectral peak period Tp(e-h)in the Beibu Gulf

4.2 北部湾海浪的驱动因素分析

局地风和南海传入浪是控制北部湾波浪条件的重要驱动因素[20]。为辨析二者对北部湾海浪的驱动贡献，本节在北部湾波浪模型试验S0的基础上开展了两组对比模拟试验，分别为仅考虑局地风作用的试验S1和仅考虑传入浪影响的试验S2。

图7a至图7h分别给出了两组对比模拟试验所得月平均有效波高的空间分布情况。在局地风作用下，北部湾内的有效波高在东北季风期自东北向西南逐渐增大（图7a），在西南季风期自西南向东北逐渐增强（图7c），在季风转换期自东南向西北增加（图7b，图7d）；局地风驱动下的湾内波浪强度以东北季风期最为强盛。在南海传入浪影响下，有效波高自湾口向湾内逐渐减小，其中，北部湾口海南岛西南海域以冬季为最强（图7e），海湾中部和北部海域则在夏季（图7g）和冬夏转换季（图7f）略大。

图7 不同驱动因素模拟得到的月平均有效波高Hs（a-h）以及有效波高贡献比RLWD（i-l）和RIWV（m-p）Fig. 7 Distributions of month averaged significant wave height Hs(a-h) and contribution percentage RLWD(i-1) and RIWV(m-p) to Hsby different driving factors

为定量评估不同驱动因素对北部湾波浪的影响，分别定义局地风和传入浪对有效波高的驱动贡献比RLWD和RIWV，公式分别为

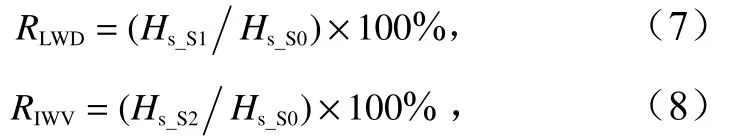
式中，Hs_S0、Hs_S1和Hs_S2分别为S0、S1和S2 3组试验下计算的有效波高值。

图7i至图7p分别给出了研究区域内各月平均的RLWD和RIWV分布情况，可见局地风和传入浪对北部湾波浪的驱动贡献此消彼长且随季节而变。局地风对海湾波浪的驱动贡献自湾口向湾内逐渐增加，冬季（图7i）和夏季（图7k）强于季风转换期（图7j，图7l）；传入浪的驱动贡献自湾口向湾内逐渐减小，季风转换期（图7n，图7p）强于冬季（图7m）和夏季（图7o）。在海南岛东部和南部海域，海浪主要受到传入浪的控制，其对有效波高的驱动贡献比在各季均高于80%，明显强于局地风的作用；在海南岛西南海域，波浪受到传入浪和局地风的共同控制，空间变化上自东南向西北逐渐由传入浪的影响占优转变为局地风的作用占优；文献[20]通过对ERA-Interim多年风浪后报资料分析指出，在北部湾湾口，年均有效波高的长期增长趋势即是受南海传入浪影响所致。在北部湾中部和北部海域，局地风对有效波高的驱动贡献比在各季均高于80%，北部高于90%，明显强于传入浪的驱动贡献，这说明海湾中部和北部海域的波浪主要受局地风控制，以风浪为主，波浪的大小可由风确定[21]；传入浪对海湾中部和北部海域的影响在冬夏季风转换期最强，这亦与文献[21]关于涌浪在4-5月出现最多的观测结果相符。

5 结论

利用NCEP发布的CFSV2再分析风场驱动SWAN模型，采用嵌套计算方案，对北部湾整年逐时海浪进行了数值模拟，对结果的检验评估显示模型具有良好模拟效果：较Jason-2卫星有效波高观测值，模拟值的均方根误差约为0.4 m，分散系数约为0.2；较北部湾湾顶近岸浮标观测数据，有效波高和平均波周期的均方根误差分别约为0.2 m和0.6 s，分散系数分别约为0.4和0.2，平均波向的均方根误差约为30°；较2′×2′的模型模拟值，空间网格为12′×12′的模型对北部湾20 m以深开敞海域波浪模拟的平均相对误差在10%以下；细化空间网格尺度有助于湾内近岸浅水域和琼州海峡区海浪的模拟。

数值模拟结果分析和驱动因素敏感性试验表明，北部湾的盛行浪向和波浪强度具有显著的季节变化，这是局地风和南海传入浪的季节变化所致，且二者对海湾波浪场的驱动贡献此消彼长、因地随季而变：局地风的驱动贡献自湾口向湾内逐渐增强，季风期强于季风转换期；传入浪的驱动贡献自湾口向湾内逐渐减弱，季风转换期强于季风期；海湾中部和北部海域以局地风为主控因素，海南岛南部和东部海域以传入浪影响为主，海南岛西南海域受局地风和传入浪的共同控制。