Exploring fundamental laws of classical mechanics via predicting the orbits of planets based on neural networks

Jian Zhang(张健), Yiming Liu(刘一鸣), and Zhanchun Tu(涂展春)

Department of Physics,Beijing Normal University,Beijing 100875,China

Keywords: neural networks,planetary orbit,conserved quantity

1. Introduction

Nowadays, with the flourishing development of artificial intelligence(AI),[2,3]machine learning has become a new“smart” tool for analyzing experimental data in fundamental science, such as astrophysics,[4,5]biological physics,[6,7]condensed-matter physics,[8-13]engineering mechanics,[14]high-energy physics,[15]statistical physics,[16-21]and so on.It is the latest trend to discover fundamental laws of physics based on machine learning without prior experience about physics. Zhao[22]inferred the dynamics of two models including a representative model of low-dimensional nonlinear dynamical systems and a spatiotemporal model of reactiondiffusion systems.He found that,instead of establishing equations of motion,the learning machine could be uesd to infer the dynamic properties of“black-box”systems. Itenet al.[23]investigated a toy system consisting of the Sun,Mars and Earth by building a neural network named SciNet. Although the training data only contain angles of Mars and the Sun as seen from Earth,they found that the SciNet could switch these angles to a heliocentric representation. This finding implies that the SciNet can gain conceptual insight that the solar system is heliocentric. Qin[24]predicted the orbits of planets in the solar system by designing a method for learning and serving. It is found that the algorithm could learn Kepler’s laws to some extent. In view of these works,we believe that neural networks will bring infinite possibilities for research. In this paper, we employ gated recurrent unit(GRU),[25-27]one of the common neural networks,to explore the fundamental laws of classical mechanics via predicting the orbits of planets. Although the training data only contain position information of planets and the Sun in geocentric system,we find that the Sun is crucial to the generalization ability of neural networks, which inspires an insight that the solar system is heliocentric. We further obtain the evidence for the existence of conserved quantities by making mutual predictions between position and velocity of planets in heliocentric system. The rest content of our paper is organized as follows. In Section 2, we introduce the data of planetary position and velocity and structure of the neural network we adpot. In Section 3, we present our results on the prediction of planetary orbits in geocentric system. In Section 4,we explore the existence of conserved quantities in mechanical systems. The last section is a brief summary and discussion.

2. Data set and structure of neural network

The initial data of planetary position and velocity in the heliocentric system come from Jet Propulsion Laboratory Planetary and Lunar Ephemeris DE421.[28]We obtain timedependent data sets of planetary position and velocity in the heliocentric system by solving a set of differential equations governed by Newton’s second law and the law of universal gravitation with time interval 0.01 years (Earth years). Here,we merely consider gravitation between the Sun and planets.The data of planets and the Sun in geocentric system are obtained by subtracting the data of the Earth from the data in heliocentric system. We regard these data as true values of“experimental”data.

Fig.1. Graphical illustration of the neural network: (a)gated recurrent unit,which includes the reset gate r,the update gate z,the activation h,and the candidate activation ˜h;[25,26] (b) the structure of neural network we use, which consists of an input layer, a hidden layer, and an output layer. Note that panel(a)is the concrete structure of each hidden neuron in panel(b).

Recurrent neural network[29]has been widely used in processing time-series beacuse of its powerful fitting ability.[30]GRU is an improved model of recurrent neural network as shown in Fig. 1(a). The main characteristic for GRU[25,26]is controlling the update of information by introducing gating units, which include a reset gater, an update gatez, an activationh, and a candidate activation ˜h. The structure of the neural network in this work is shown in Fig. 1(b). The neural network contains one hidden layer, which is composed of GRU and fully connected with an input layer and an output layer. We use supervised learning algorithm and carry out our work with Keras[31]running on top of Tensorflow.[32]

3. Prediction of planetary orbits in geocentric system

In this section, we use the neural network to predict the orbits of planets which consist of Venus, Mars, and Jupiter.The detailed hyperparameters of the neural network are shown in Table 1. The input layer and output layer contain 10 neurons and 1 neuron,respectively. The training set contains 14-year data,totally 1400 samples,and the test set contains 4-year data,totally 400 samples.

The data processing is given below. We train the neural network to learn a mappingf:

through the training set,whereUnis an element of time-series.Then we use the trained neural network to predict planetary orbits. During the training,all inputUn(n=1 to 1400)are true values in training set. During the prediction,we merely input ten true values ofUn(n=1401 to 1410)in test set. And then we output the predicted values ofUn(n=1411 to 1800).

The neural network operates on two types of data in geocentric system. One merely includes the position information of a planet,i.e.,Un= (xan,yan,zan), wherexan,yan, andzanare the coordinates of the planet in geocentric system. Another includes simultaneously position information of a planet and the Sun in geocentric system,i.e.,Un=(xan,yan,zan,xsn,ysn,zsn),wherexsn,ysn, andzsnare the coordinates of the Sun. We normalize the data with constantXmax-Xmin, whereXmaxandXminare the maximum and the minimum ofxanforn= 1 to 1400, respectively. For example,yanis transformed into(yan-Xmin)/(Xmax-Xmin).

第(Ⅰ)问求解时，不论学生使用正弦定理还是余弦定理，都会求得cos∠ADB的两个解，学生需要结合题设条件舍弃一解．此问考查学生思维的严谨性，有部分学生正是因为缺乏这样的基本数学素养失分．

Table 1. Hyperparameters of the neural network in Section 3.

Table 2. Test errors of prediction for planetary orbits in Fig.2.

The predicted orbits of Venus, Mars, and Jupiter are shown in Fig.2. Each figure contains two curves. The dashed line represents true orbit, and the solid line represents predicted orbit. We show the result without considering information of the Sun in the left column. And we show the result with information of the Sun in the right column. By glancing at these images, we find that the predicted values are closer to the true values when considering the Sun. As shown in Table 2, we calculate the test errors (mean squared error) by comparing the predicted values and the true values. The precision for predicted cruves has been significantly improved with the information of the Sun.

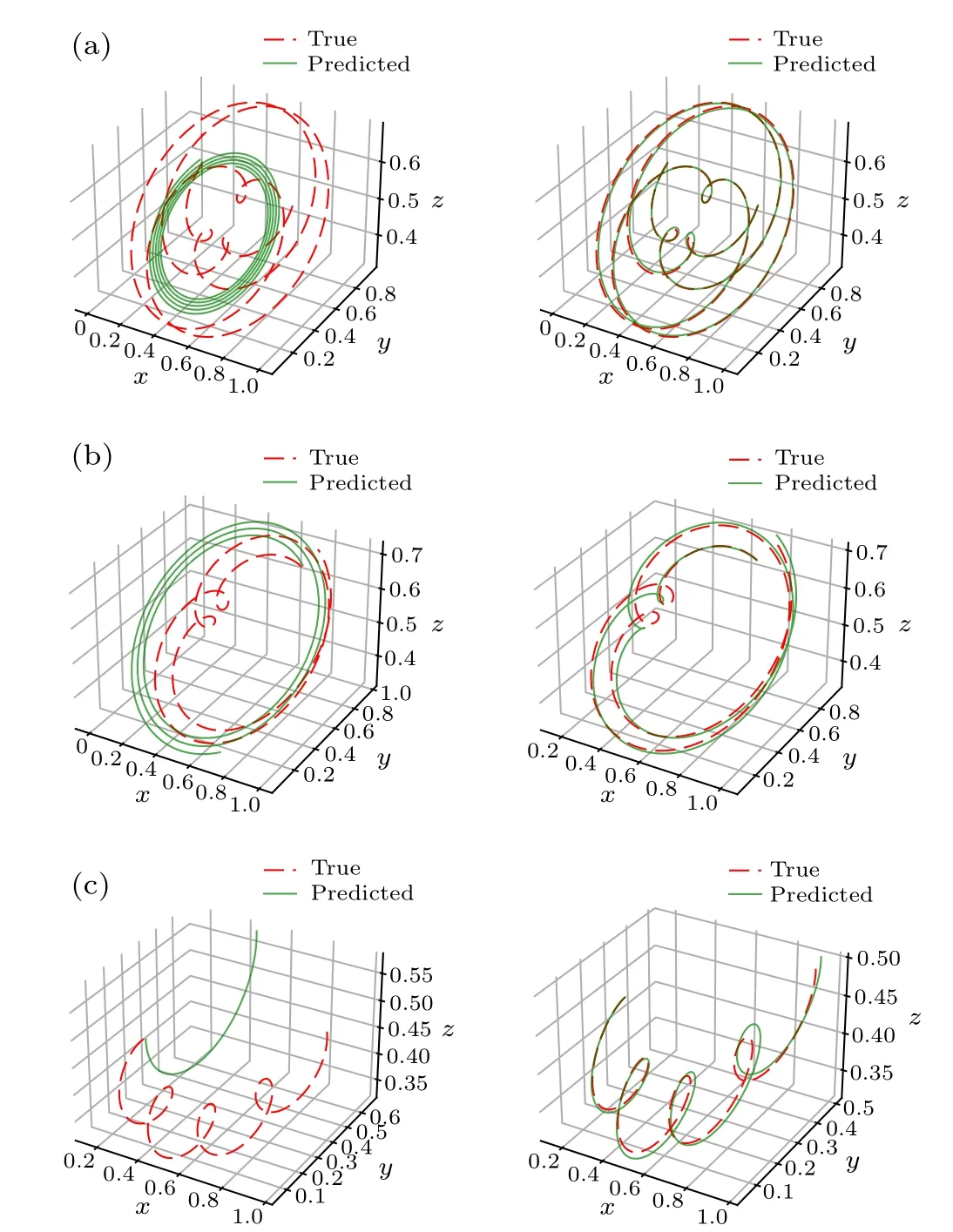
Fig. 2. Images of planet orbits. The dashed line represents the true values,and the solid line represents the predicted values. The results without considering information of the Sun is on the left, and the results with information of the Sun is on the right. (a)Orbit of Venus. (b)Orbit of Mars. (c)Orbit of Jupiter.

We also predict orbits of planets with information of another planet rather than the Sun. We predict orbits of Venus and Mars with information of Jupiter. As shown in Fig.3,the precision of prediction decreases obviously. Without any prior knowledge, these facts imply that the Sun is particularly important in the model system including Venus, Mars, Jupiter,the Earth, and the Sun. In a way, this finding based on neural networks helps us to gain Copernicus’heliocentric theory.This is one of the main results in our paper.

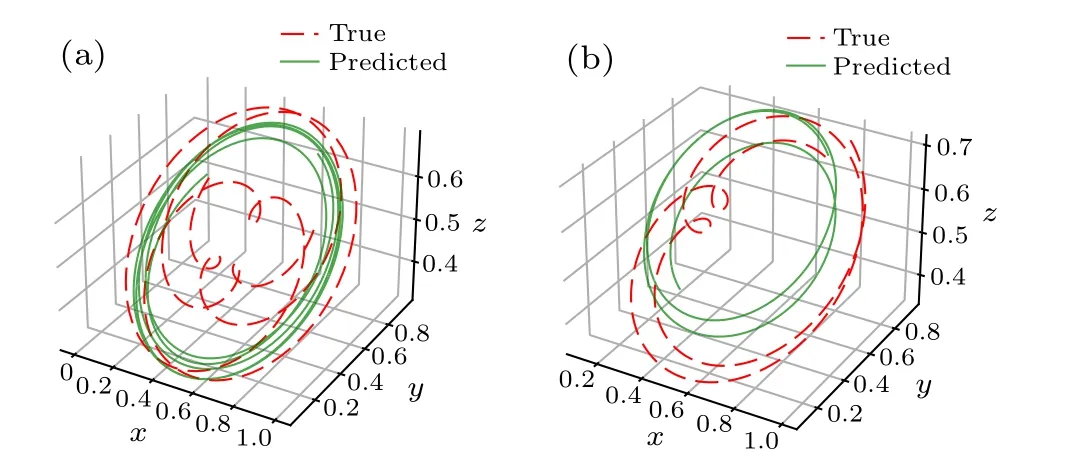
Fig.3. Images of orbits with information of Jupiter rather than the Sun. (a)Orbit of Venus. (b)Orbit of Mars.

4. Evidence for the existence of conserved quantities

According to the universal approximation theorem,[34,35]the reason for successful prediction is that neural networks can learn a mapping from big data. The predicted results of neural networks may indicate whether there are conserved quantities in a mechanical system. We propose that if there are enough conserved quantities in a system,neural networks can successfully learn the mapping between positon and velocity. In order to explore the existence of conserved quantities, we turn to a model system including Venus, Mars, and Jupiter in heliocentric system since we have found that the Sun plays a very important role in predicting orbits in the previous section.

We adopt the same structure of neural network shown in Fig. 1. Unlike in the previous section, here the input layer and output layer only contain one neuron, respectively. The training set contains 14-year data of position and velocity in heliocentric system,totally 1400 samples,and the test set contains 12-year data,totally 1200 samples. The hyperparameters of the neural network are shown in Table 3.

Table 3. Hyperparameters of the neural network in Section 4.

To demonstrate our idea further, we choose two timedependent series. One is the data of velocityvn=(vnx,vny,vnz), wherevnx,vny, andvnzare the components of velocity for a planet in heliocentric system. The other is the data of positionrn=(xn,yn,zn), wherexn,yn, andznare the coordinates of the planet in heliocentric system. We normalize the data of velocityvnwith constantVmax-Vmin, whereVmaxandVminare the maximum and the minimum ofvnx. We normalize the data of positionrnwith constantRmax-Rmin,whereRmaxandRminare the maximum and the minimum ofxnforn=1-1400,respectively.

We use the neural network to predictvnfromrn. In training set,rn(n=1-1400)are the features andvn(n=1-1400)are the labels. During the prediction,we inputrn(n=1401-2600)in test set. And then we output the predicted values ofvn(n=1401-2600).

Predicted hodographs of Venus, Mars, and Jupiter are shown in the left column of Fig. 4. The small deviation between the predicted values and true values implies that the neural network have learned the mappingg:

Similarly, we use the neural network to predictrnfromvn.The predicted orbits of Venus,Mars and Jupiter are shown in the right column of Fig. 4. The deviation between the predicted values and true values is also small. For each of the three planets,we also use data of 3/4 period in training set to predict data of one period in test set, respectively. And these mutual predictions are similar to Fig.4.

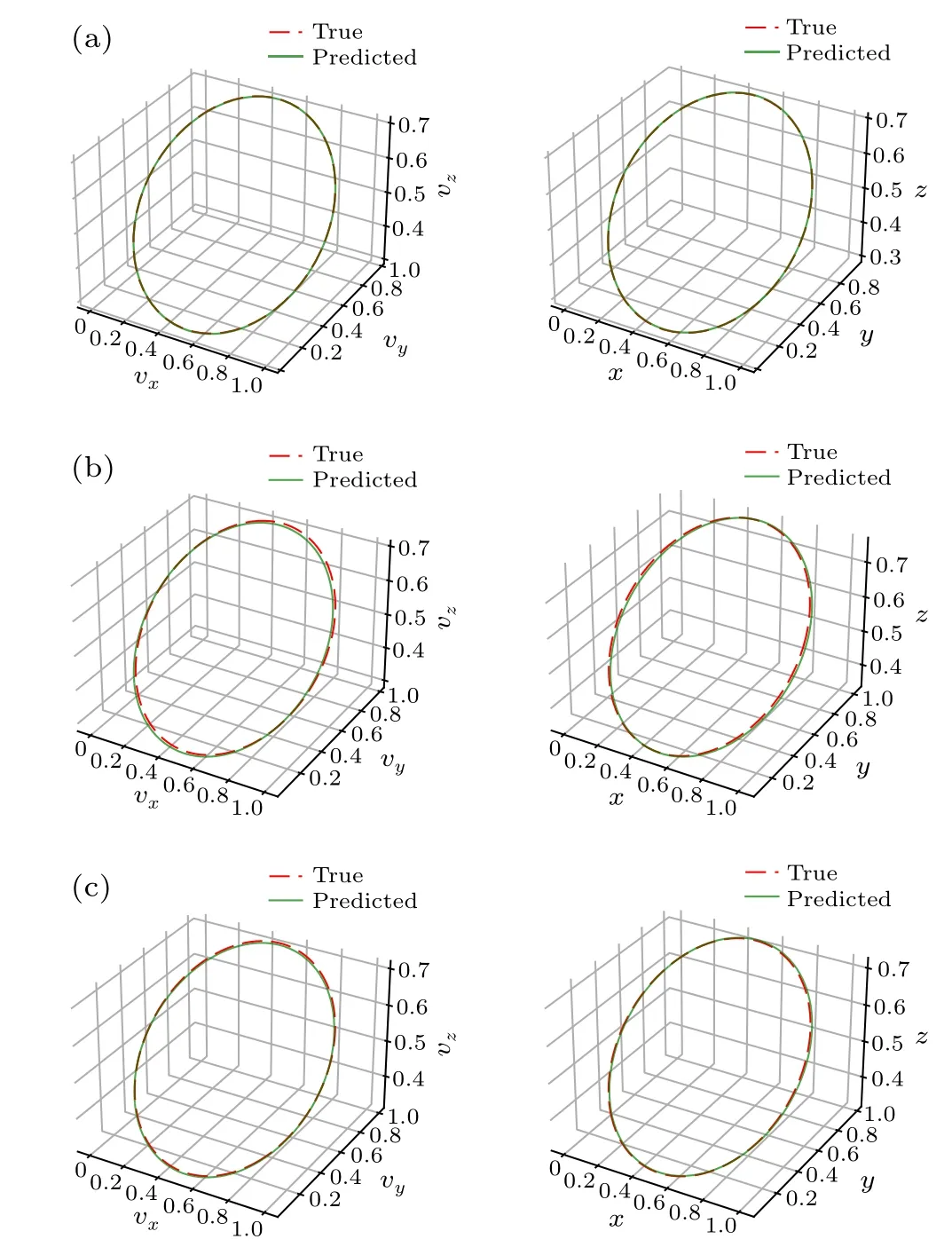
Fig.4. Mutual predictions of velocity and position for planets. The left column is predicted hodograph from position. The right column is predicted orbit from velocity. (a) Predicted resluts of Venus. (b) Predicted resluts of Mars. (c)Predicted resluts of Jupiter.

The vector mapping (2) contains three scalar relations which represent three first integrals for planetary motion in heliocentric system. As we know,planetary motion satisfies the conservation of mechanical energy and conservation of angular momentum. The mechanical energy of the system is expressed as one independent relation wherevis the speed of the planet.ris the distance between the planet and the sun,mis mass of the planet.kis the stress of gravitation.Eis the mechanical energy.

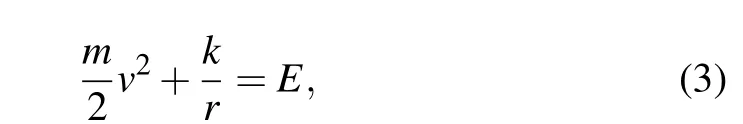
The angular momentum of the system has three componentsLx,Ly,andLz. According to poisson theorem,ifLxandLyare conserved quantities,Lzis also a conserved quantity.[36]Thus,the conservation of angular momentum merely contains two independent relations

wherevx,vy, andvzare the components of velocity for the planet.x,y,andzare the coordinates of the planet. Therefore,three independent relations of conserved quantities are satisfied in planetary motion. Equations (3)-(5) should be equivalent to Eq.(2). Since we can solve the relationship between velocity and position from Eqs.(3)-(5)in principle.But we do not know the specific correspondence between these relations[Eqs. (3)-(5)] and the three first integrals hidden in Eq. (2)learned by neural networks for planetary motion in heliocentric system.

We infer that the neural network can successfully learn the mapping(2)when the number of first integrals are equal to the dimension of data,instead of learning the differential relationship between velocity and position. To further verify our idea, we discuss an example where the number of conserved quantities is less than the dimension of data in a mechanical system. The planar motion of a particle in a time-dependent central force field can be expressed as

whereris position vector. The initial velocity isv0=(0,1)and position isr0=(0.5,0). There is only one independent conserved quantity (conservation of angular momentum) in this system. Using the same neural network and data processing as planetary motion in heliocentric system,we continue to make the mutual prediction of position and velocity. The data set includes time-series of velocity and position with the time interval of 0.5. The training set contains data of 6000 samples,and the test set contains data of 4000 samples. The hyperparameters of the neural network are the same as Table 3.

The predicted results are shown in Fig.5. Obviously,the mutual predictions of position and velocity are very bad. We also obtain the same conclusion for time step 0.1 and 0.01.This example reveals that the neural network we adopt fails in predictions when the number of conserved quantities is less than the dimensions of data, although there is a differential relationship between position and velocity.

These results mentioned above suggest the strong correlation between the existence of conserved quantities in mechanical system and the predicted quality of neural networks. This is the second main result in our paper. Our research provides a new way to explore the existence of conserved quantities in mechanical system based on neural networks.

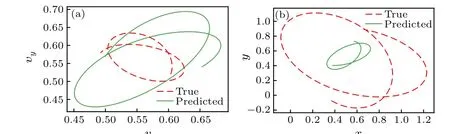
Fig. 5. Mutual predictions of velocity and position for a particle in a timedependent central force field. (a) Predicted hodograph from position. (b)Predicted orbit from velocity.

5. Conclusion

In the above discussion, we make a new attempt to gain physical insights underlying big data by using neural networks. In this sense,the simpler neural network is,the closer it is likely to the human thought. We have accomplished the goal perfectly with GRU,one of the common neural networks.On the one hand,we find that the precision of predicting orbits in geocentric system strongly depend on whether the data of the Sun is included in training set or not. When considerating the information of the Sun,we make successful prediction of planetary orbits. We fail in prediction without the information of the Sun. Even for Mercury,we also arrive at the same result. We merely need to change the time interval to 0.001 years, because Mercury has a short period of motion. This striking contrast suggests that the Sun is of great significance in geocentric system and further hints the solar system is heliocentric. On the other hand,we make the mutual prediction of position and velocity in mechanical systems. We demonstrate that the reason for successful prediction is the dimension of system is equal to the number of first integrals. This provides an evidence for the existence of conserved quantities in mechanical system. We emphasize that our work does not imply the impossibility of learning a dynamic process where there exist no orbitals (e.g., the chaotic systems). For these systems,the research of learning dynamics from data has been explored,such as the work of Zhao.[22]

Liu[37]predicted the orbits of planets by long short-term memory network,and the results are qualitatively and quantitatively consistent with the present work. We also use fully connected neural networks to explore the existence of conserved quantities and come to the same conclusion. These suggest that our conclusions are of a certain universality. Recently, AI physicist[38]has opened and represents a new research paradigm.Our work contributes a footnote for a special AI physicist. In the future,we hope to clarify the specific correspondence between the three conserved relations[Eqs.(3)-(5)] and the three first integrals hidden in Eq. (2) learned by neural networks for planetary motion in heliocentric system.It will be an exciting mission to use neural networks to discover physical laws directly, which will be a promising road to scientific research.

Acknowledgments

The authors would like to thank Xinran Ma for the helpful discussion in machine learning.

Project supported by the National Natural Science Foundation of China(Grant No.11975050).