岩石爆破的损伤理论及损伤模型研究

刘 露

（重庆交通大学河海学院，重庆 400041）

0 引言

岩体爆破在大型水利工程、采矿行业中应用十分广泛。但是在爆破过程中，会对周围岩体产生一定程度的损伤，影响周围岩体的安全性。岩石爆破理论一直以来是众多学者关注的重点，岩石爆破理论先后经历了流体弹塑性模型、断裂模型和损伤模型几个阶段，虽然有许多学者建立相应的模型，但模型的准确性以及适用性仍是需要进一步研究的重点。因此，选择合适的模型来描述岩石在爆炸荷载作用下的动态力学行为尤为重要。

1 损伤理论

岩石在外荷载作用下的破坏过程，是随着作用荷载的增加，岩石内微裂隙空隙增多、扩展从而相互贯通，形成宏观裂纹，最终破坏解体的过程。

根据对岩石损伤力学研究，损伤一般指的是材料内部的一种劣化因素，与材料和周围环境有关。通过引入表征材料内部对于微小裂隙以及细微的材料缺陷的损伤变量，参考损伤变量建立损伤模型，依据连续介质力学理论和不可逆热力学理论，建立关于损伤的本构方程，使用损伤变量广义地描述细观损伤劣化的作用和影响，建立相关损伤演化方程，据此对材料的损伤进行相关分析。

岩石损伤的存在和发展会导致岩体中应力波波速的衰减，所以波速衰减和定义参数间的关系对应力波的传播具有极其重要的作用。关于损伤的定义最早是由L.M.Kechanov提出的，经过不断的发展，关于岩体损伤的试验开展得很多，对于损伤模型的建立，国内外学者也取得了很多的成果。现有爆破损伤本构模型通常为各向同性的模型。Taylor等[1-2]建立的关于岩石的各向同性损伤力学模型，代表了岩石爆破理论模型的发展方向，常被称为TCK爆破损伤模型。该损伤模型为经典的体积拉伸损伤模型，认为岩石的损伤劣化是因为其内部微裂隙的发育导致的，将岩石的动态断裂过程处理为一个连续的损伤累积过程，其中损伤机制归因于一个预先存在的微裂纹网络的增长和相互作用。Ortize[3]，Lubarda等[4]提出了一个形式比较复杂，但是适用于一般情况的模型，认为岩石的非弹性变形主要原因在于裂纹的滑动和摩擦形成裂纹的闭合。Chaboche[5]和Voyiadijs[6]等也提出了相应的损伤模型，研究了岩石材料的塑性和损伤的耦合问题和弹塑性理论。杨军[7]等通过引入岩石动态损伤参量及其表征方式以构建岩石爆破损伤的模型。Yang等[8]提出了一种简单的爆破损伤本构模型，用于模拟应力波的冲击载荷引起的岩石损伤,该模型假设爆破过程中岩石的脆性破坏受拉伸应变控制。杨小林等[9]参考现有关于岩石爆破损伤机理的研究，和岩石细观损伤力学理论基础，提出了关于岩石爆破损伤断裂的细观理论。陈俊桦等[10]对yang等提出的爆破损伤模型进行了改进，建立了考虑初始损伤的弹塑性爆破本构模型，并提出用于评价围岩受爆破影响的损伤判据。李心睿等[11]基于宏观统计损伤模型，考虑动荷载作用下造成的岩体初始损伤以及静荷载损伤两者间的耦合作用，建立了修正的裂隙岩石试样损伤演化本构方程。胡英国等[12]对目前应用较为广泛的爆破损伤模型进行了相关总结分析，列举了部分关于损伤变量的定义方法。

2 损伤模型

当前，关于岩石爆破的损伤理论模型有很多。其中，损伤模型间的区别主要在于各个模型对损伤变量的定义不同；但大多数模型都会采用岩石中的裂隙数量以及密度来定义相关损伤变量。关于岩石的损伤模型主要以裂纹密度、损伤的演化规律以及使用有效模量三个方面组成岩石的本构方程。本文中，主要介绍引用较多的KUS损伤模型、K-G模型和yang等人建立的有关岩石损伤的模型。

2.1 K-G损伤模型

关于K-G损伤模型，最早是由美国学者Kipp和Grady提出，损伤计算模型中假设岩石中含有大量的原生裂纹，且岩石中裂纹的空间分布是随机的，采用一个标量描述被拉应力激活的裂纹引起岩体刚度的劣化，在外荷载作用下，其中的裂纹被激活并发育。裂纹数符合指数分布：

式中：n(εv)——被激活的裂纹数；

εv——体积应变；

k，m——材料常数。

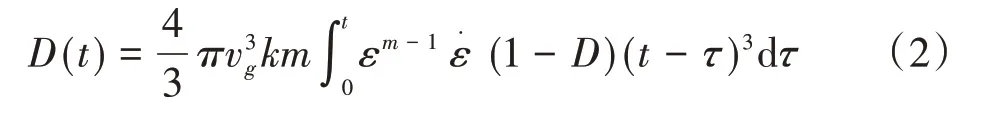
式中：D(t)——t时刻的损伤；

vg——裂纹扩展速率；

ε.——体积应变率；

k，m——材料常数。

总的破坏面积A(t)为：

式中：N.——裂隙激活率；设裂纹平均半径为a-(t)；则近似为

由此可以推得裂纹的平均间距，也可认为平均的破碎尺寸Lm为：

岩石损伤后，本构关系可以表示为：

式中：K——体积弹性模量；

G——拉美常数。

式（1）～（6）便定义为关于K-G损伤模型相关理论的封闭方程组，方程中材料常数k、m、Cg通过拉伸试验的应变率确定。

2.2 KUS损伤模型

KUS损伤模型是根据K-G相关损伤模型的发展得到的，两个模型的主要区别在于，两者关于岩石材料的描述不尽相同。其中，KUS损伤模型认为，当模型中的岩石材料处于体积拉伸或静水压力为拉应力时，岩石中自身存在的裂隙将会由于其应力被激活，导致裂纹激活便立即影响周围的岩石，从而使周围的岩石材料释放应力，裂纹发生扩展。其中，裂纹密度Cd定义为裂纹影响区的岩石体积与岩石总体积的比值：

N——裂隙激活率，其中关于N的定义与K-G损伤模型中的定义相同。

KUS损伤模型中，假设应力激活的裂隙平均半径与碎块的平均半径成正比，具体公式如下：

式中：α——自定义的比例系数；

ρ——岩石密度；

C——岩石中的波速；

KIc——掩饰的断裂韧性。

裂纹密度Cd依据损伤模型假设定义可以表示为：

依据O,connel的相关研究，可将关于岩石材料含裂纹材料的裂纹密度、有效泊松比、损伤因子关系如下式所示：

上式构成了关于KUS损伤模型的封闭方程组。

2.3 Yang等人的模型

Yang等人建立的相关模型认为，岩石中裂纹的发育主要取决与岩石材料的延展应变，假设岩石中某点的延展应变大于一定大小的临界值时，岩石中原有的裂纹便会出现起裂和扩展现象。其中，关于岩石的延展应变定义为岩石中某点的主拉应变之和，如：

式中：θ——延展应变；

λi——主延伸；当Inλi为压缩时，Inλi=0，当Inλi为拉伸时。

损伤模型中定义了当岩石材料的延展应变大于某一个临界值时，岩石中的裂纹将会扩展发育，此时岩石中裂纹密度的增加量可由下式表示：

式中：fs——岩石中裂纹的密度；

α、β——岩石材料的相关常数；

θ、θc——分别为岩石材料的延展应变以及临界延展应变，其中，临界延展应变取值为θc=0.2～0.22。

损伤模型中定义了损伤因子D表示为下式：

其中，损伤模型中定义的关于岩石损伤前后的弹性常数之间关系如下式所示：

式中：E、G、μ——分别为损伤模型中未损伤岩体中的初始弹性模量、剪切弹性模量和泊松比，ED、GD、μD则表示岩石材料受到损伤后的相应的参数大小。

3 结束语

（1）现在关于爆破损伤的研究很多，由于实际岩体往往各方向力学性质差异很大，显现出各向异性，大多数损伤模型假设岩体是均质的，各向同性，因此，理论推导和实际测量有一定的差异。对现有模型进行改进，往往能适用于不同岩体条件下的工程，由此对爆破损伤理论应用范围进行拓展。

（2）实际工程中，岩石爆破中破碎区岩体的动力本构关系往往十分复杂。因此，爆破动力本构模型的研究还需要进一步探究。不同模型的选取由于假设条件的差异，可能会导致结果有很大的差异，但是对于实际工程的应用仍然具有一定的参考价值。