动静转换 化繁为简

⦿浙江省宁波市仁爱中学 王雪君

1 引言

我们常说“动静结合”，其实从某种角度而言，动和静之间并不存在本质性的差异，只是所选择的参照物不同而已.以静止的物体为参照物，才能体现出其他物体的动态性.如果以动态的物体为参照物，那么静止的物体才是运动的.因此可以知道，动和静之间始终是存在相互转化的.在数学领域中，我们可以采用动静结合的方式进行转换，从而降低数学问题解答的难度，而且也能够通过这样的方式有效提高数学问题的实际性解答效果.比如在数学问题上，我们可以利用相对运动观念，把原来运动的图形看成静止的，把原来静止的图形看成运动的，这样不仅能为解决问题提供新的手段，往往还能达到化繁为简的效果.下面结合具体实例说明.

2 动静转换典例分析

例1(2017年浙江舟山嘉兴)如图1所示，一副含30°和45°的三角板ABC和DEF叠合在一起，其BC边和EF边重合，且AB和DC相交于点H.现在知道BC边(即EF边)的长度为12 cm，G为边BC的中点.

(1)BH的长度为.

(2)现将三角板DEF绕点G按顺时针的方向旋转60°，如图2所示，在三角板DEF转动的过程中，点H移动的距离为.(结果保留根号)

图1 图2

分析：本题第(2)问中点H的运动过程比较复杂，直观的感受是BH的长度慢慢变短，因此很多人都把初始状态和结束状态算一下就得出了结果.造成这种情况是因为在运动过程中很难看出BH长度变化.但利用相对运动的观念，把三角板DEF看成不动的，三角板ABC绕点G逆时针旋转60°，这样就很容易看出GH长度的变化是先变小，当GH⊥DF时，GH最小，然后再逐渐变大.根据GH的值，我们可以求出BH的值，于是就很容易得到结果，问题就转化成了解直角三角形问题[1].

解:(1)如图3，当BC和EF重合时，作HM⊥BC于点M.设HM=CM=x.

∵∠ABC=30°，∠BCD=45°，

图3

图4

(2)如图4，当GH⊥DF时，GH最小，此时BH也最小.作GN⊥AB于点N.

∵∠F=45，GF=6，

∵BG=FG=6，∠ABC=30°，

∴NH=3.

图5

如图5，当点H和F重合时，

∵GF=BG，

∴∠GBF=∠GFB=30°.

图6

图7

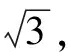
点P从点A运动到点O的过程中，点Q的运动路程为1.

综上所述，点Q运动的总路程为4 cm.

例3(2013年天津)如图8，在平面直角坐标系中，已知点A(-2,0),B(0,4),点E在OB上，且∠OAE=∠OBA.

(1)略；

(2)如图9，将△AEO沿x轴向右平移得到△A′E′O′，连接A′B，BE′.

②当A′B+BE′取得最小值时，求点E′的坐标.

图8 图9

分析:本题的第(2)问，如果用代数法解决，会出现两个二次根式.欲求其最值，在初中阶段有一定的难度，显然考虑用几何法解决.此题中，点B为定点，线段AE水平向右移动，这种情况学生也不熟悉，对于标答提供的构造全等的方法，虽然非常巧妙，学生却不易想到.若利用相对运动，将线段AE看成静止的，点B水平向左运动，问题就转化成了学生熟知的将军饮马问题了[2].

解:(1)略；

(2)如图10，过点B作直线l平行于x轴，取点F与A关于l对称，连结FE交l于点B′，显然AB+BE≥AB′+BB′EEF.

图10

由A(-2，0)，B(0，4)，

可得F(-2，8)，E(0，1).

设直线y=kx+b过点F，E，

即直线EF的解析式为

(1)略；

(2)略；

(3)如图12，现将△BDP绕点B逆时针旋转，得到△BD′P′，当∠PBP′=∠OAC，点P的对应点P′落在坐标轴上时，求P点的坐标.

图11

图12

分析：第(3)问的难度较大，首先，很难判断具体有几个点P，然后有些点P的坐标也较难计算.当△BDP绕点B逆时针旋转，可简化为线段BP绕点B逆时针旋转.由于点P为抛物线上的点，问题就转化为：整个抛物线绕点B逆时针旋转∠OAC的度数与坐标轴相交，求交点坐标.此时很容易判断这样的点有三个，同时新的问题也产生了，此时的抛物线解析式如何求.可以说，在初中阶段这样的抛物线的解析式是无法求出的.但利用相对运动的观念，我们一样可以解决问题.把抛物线看成静止的，那么坐标轴所在的直线绕点B顺时针旋转∠OAC的度数，与抛物线的交点，就是我们要求的点P，这样问题就转化成了求直线和抛物线的交点问题，可以轻松解决.

图13

解:(1)(2)略；

(3)如图13，将y轴所在直线绕点B顺时针旋转∠OAC的度数交抛物线与点P1.

由∠CBP1=∠OAC，得BP1⊥AC.

3 结束语

通过上述例题可以看出，在数学领域中，动和静之间是相互结合的，学生只有把握好动与静之间的相互转化，才能够更好地保证动点与静点之间的有效性结合，也才能够更加有效地学习和理解数学知识，切实提升数学解题能力.