高速铁路车轮扁疤载荷作用下轮轨动力响应分析

陈志贤 林红松 姚 力 杨吉忠 李忠继

(中铁二院工程集团有限责任公司, 成都 610031)

自2002年诞生第一条高速铁路以来，我国高速铁路线路及网络经历了长足的发展[1]，截至2020年底，我国高速铁路总里程已经突破3.79万km，稳居世界第一。然而，随着速度的提高，高速铁路轮轨振动不断加剧，车轮及钢轨病害出现愈加频繁。高速铁路车轮病害以车轮失圆为主，其中车轮扁疤作为车轮失圆的一种典型形式，多指车轮在启动、制动等工况下车轮抱死或低黏着状态下车轮在轨道上滑移所产生的车轮擦伤。车轮扁疤将导致车轨动力冲击加剧，轮轨力增大(静态轮重的几倍甚至数十倍)，进而造成轮轨维护成本增加，维护周期缩短。同时，车轮扁疤还会影响车辆运行平稳性、乘坐舒适度、安全性，严重时可能造成车辆脱轨及转向架部件断裂等严重安全事故[2]。

国内外学者对扁疤造成的轮轨动力响应进行了深入研究，目前已形成了一系列分析方法和理论。文献[3]根据低接头冲击力公式与扁疤冲击速度公式，引入了一种简化的扁疤冲击力计算公式，对车轮扁疤作用下的轮轨冲击力进行了计算；文献[4]对车轮扁疤的动力学效应做出了比较全面的理论分析与数值模拟，并对我国主型货车车轮扁疤长度限值进行了探讨；文献[5]建立了基于扁疤真实几何形状的三维轮轨滚动接触有限元模型，对列车速度、扁疤长度、轴重等对轮轨冲击力的影响进行了研究，揭示了扁疤条件下一些关键参数对轮轨冲击立项响应的影响规律；文献[6]建立了车辆系统整车动力学模型，采用改变车轮半径的方法模拟车轮扁疤，同时考虑车轮半径对轮轨接触状态和接触参数的影响，研究车轮新旧、扁疤引起的轮轨冲击力的变化规律，给出高速车辆车轮扁疤的安全限值；文献[7]建立了包含扁疤长度、宽度及深度的车轮踏面三维扁疤模型和车辆-轨道耦合系统动力学模型，考虑轮对旋转走行和轮轨接触几何关系，研究了高速车辆-轨道系统三维车轮扁疤轮轨冲击振动特征。

然而，以上对于扁疤轮轨冲击振动研究存在仿真车辆速度较低，不能满足更高速度的要求的问题；同时，现有研究没有将车辆系统与扁疤三维接触系统进行结合，对实际扁疤形成的条件考虑不够充足。

基于此，本文采用多体动力学软件建立了详细考虑轨道扣件系统车辆-轨道耦合模型，以造成车轮扁疤的钢轨形状为参考对扁疤的三维形状进行了准确的模拟，分析了不同扁疤长度和不同车速下的车轨动力响应。研究成果可为更高速度下轨道载荷设计提供理论及仿真依据。

1 车辆-轨道系统动力学模型

1.1 车辆系统动力学模型

为精确地模拟400 km/h级某型高速列车轨道动力学行为，本文在建模时采用了将系统横向运动和垂向运动耦合起来的数学模型。为便于分析，高速列车动力学模型中采用的假定主要包括：

(1)将轮对、构架、齿轮箱和车体等部件视为刚体，即忽略弹性变形。

(2)不考虑相邻车的影响，即模型只考虑单节车辆。

定义车辆前进方向的第一个轮对为一位轮对，坐标系的取法如下：车辆的前进方向为x轴；y轴平行于轨道平面指向右方；z轴垂直轨道平面向下。

高速动车组动力学模型由1个车体、2个构架、4个轮对共计7个刚体组成。车体取6个自由度，即纵向、横向、垂向、侧滚、点头、摇头；构架取6个自由度，即纵向、横向、垂向、侧滚、摇头、点头；轮对取6个自由度，即纵向、横向、垂向、侧滚、点头、摇头(其中轮对垂向和侧滚运动是非独立运动)。高速动车组单节车辆系统自由度总共42个自由度，如表1所示。

表1 高速列车动力学模型自由度表

车辆系统动力学模型拓扑结构如图1所示，车辆系统动力学模型参数如表2所示。

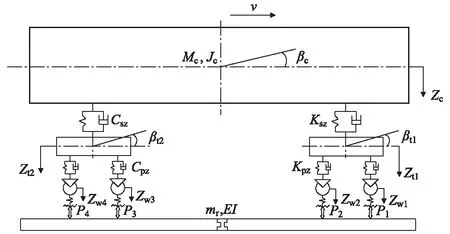
图1 车辆系统动力学模型图

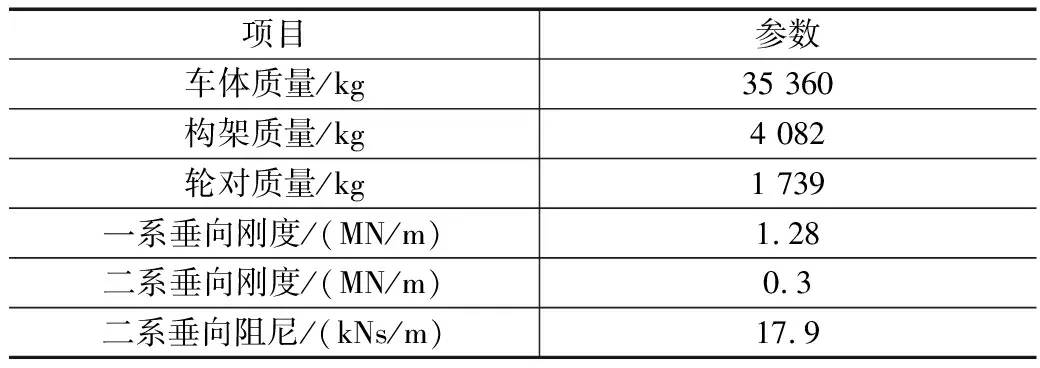
表2 某型动车组车辆参数表

1.2 轨道系统模型

根据CRTS Ⅲ型板式无砟轨道结构建立轨道模型。CRTS Ⅲ型板式无砟轨道由60 kg钢轨、WJ-8扣件系统、轨道板、自密实混凝土、土工布隔离层和底座板组成。其中轨道板与自密实混凝土浇筑在一起，在自密实混凝土与底座板之间设置土工布隔离层，底座板连接在下部基础结构上。

多体动力学软件提供了轨道建模环境，将钢轨考虑为弹性铁木辛科梁，通过扣件弹簧支撑于轨道板上。扣件为三向刚度阻尼弹簧力元，如图2所示。轨道参数取值如表3所示。

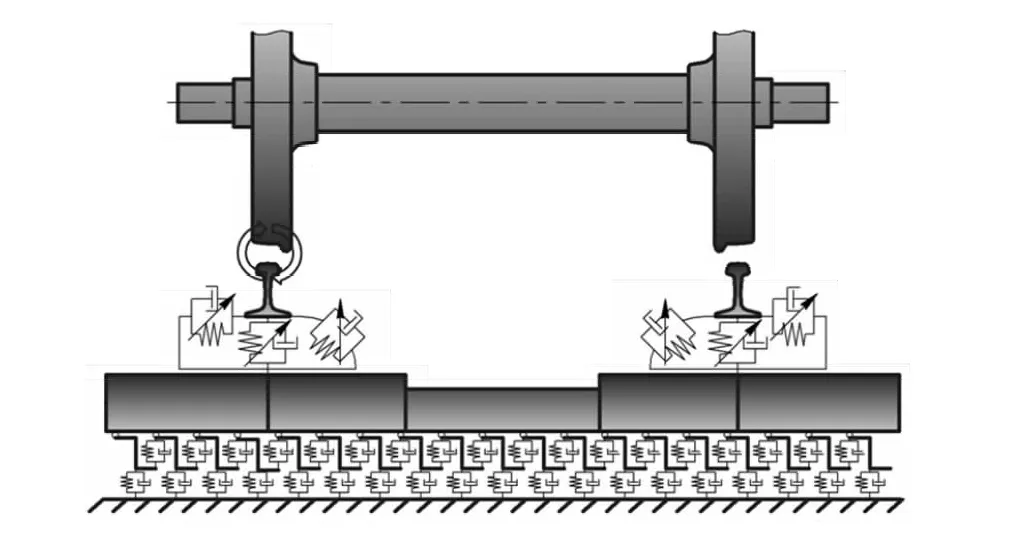
图2 轨道结构模型图

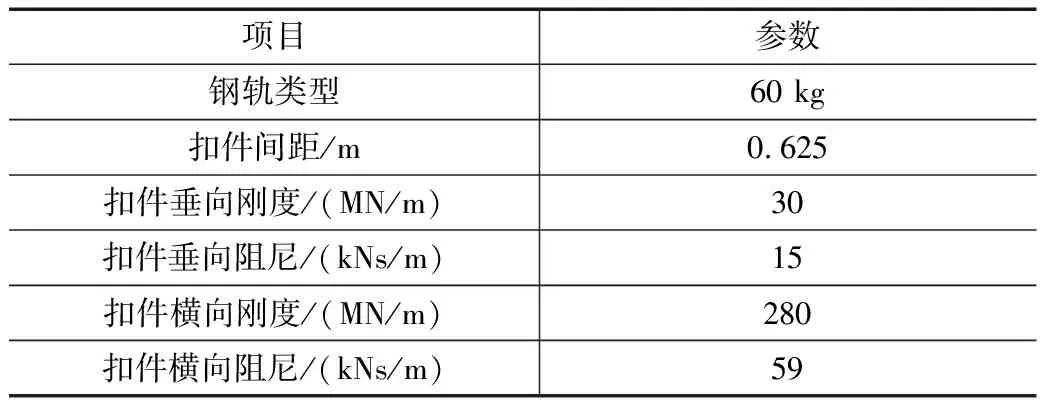
表3 轨道参数表

1.3 车辆-轨道耦合动力学模型

采用通用多体动力学软件建立车辆-轨道耦合动力学模型，如图3所示。模型中详细考虑了车辆的轮轨接触关系、一二系悬挂系统，将钢轨考虑为弹性铁木辛科梁，并对扣件系统进行了详细考虑。

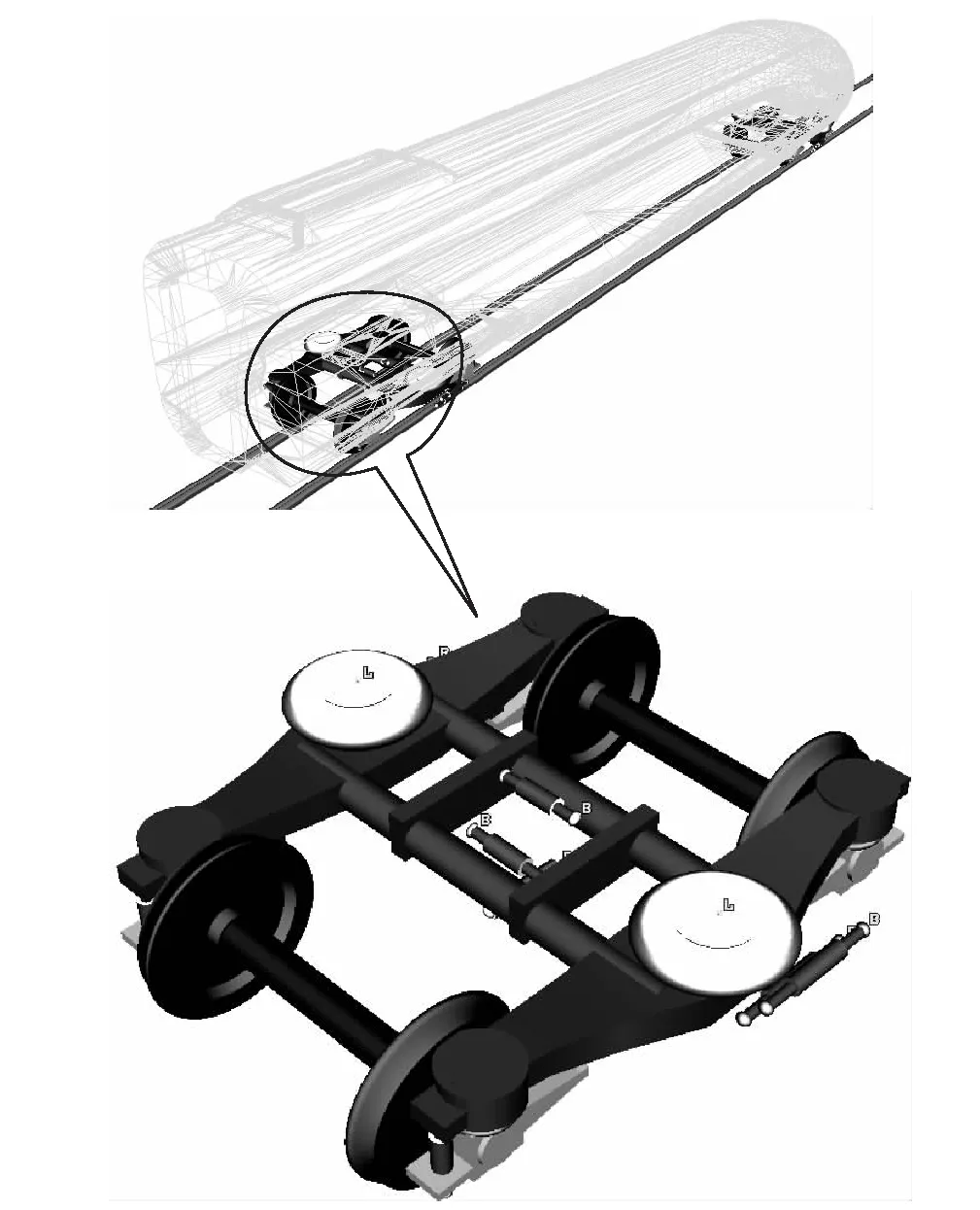
图3 多体动力学软件建立的高速车辆-轨道耦合动力学模型图

2 车轮扁疤模型

2.1 车轮扁疤二维冲击模型

车轮扁疤模型主要分为新扁疤和旧扁疤两种。新扁疤刚刚形成，可将其看作是车轮踏面圆周上的弦，而旧扁疤为新扁疤经过一定磨损以后，棱角被磨圆以后形成的扁疤。车轮扁疤模型如图4所示。

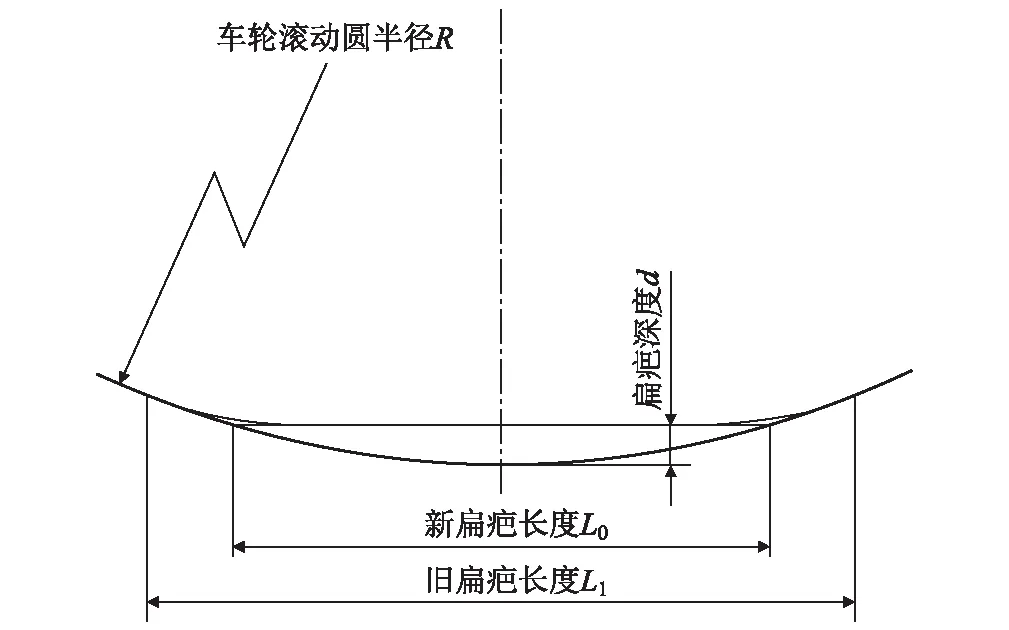
图4 车轮扁疤模型图

从二维角度对扁疤冲击进行分析，低速和高速情形下二维扁疤车轮运动情况分别如图5和图6所示。

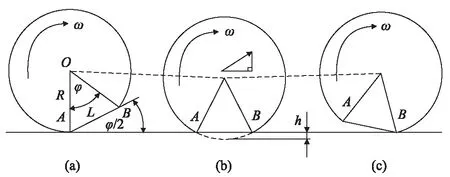
图5 较低速情形下扁疤车轮运动示意图

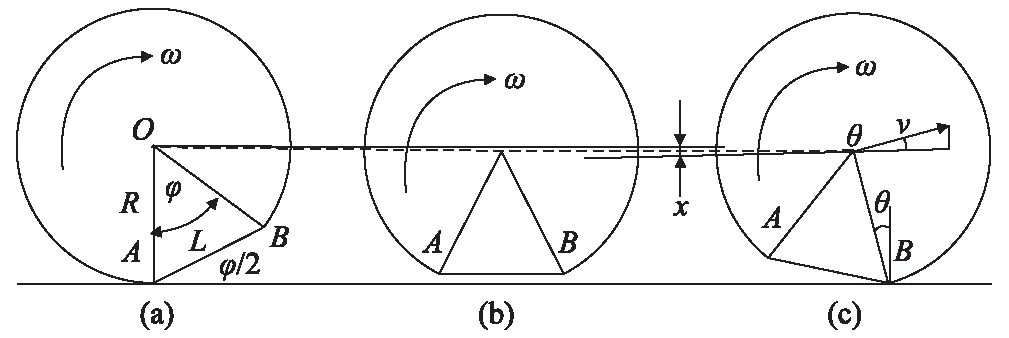
图6 较高速情形下扁疤车轮运动示意图

由图5、图6可知，在低速运行时，车轮滚动至扁疤始点A时，将绕A点旋转至整个扁疤表面撞击轨面(如图5(b)所示)，随后将继续绕B点转动，继续对轨道施加动力作用[8]。在较高速度时，车轮滚动至扁疤始点A时，由于角速度较高，导致了车轮脱离钢轨表面(如图6(b)所示)，此后车轮在旋转的同时向前惯性运动并且同时下落，将在B点重新接触钢轨(如图6(c)所示)。

2.2 车轮扁疤三维冲击模型

二维模型仅定义了扁疤的周向长度和深度，且扁疤深度由扁疤长度唯一确定。三维扁疤相较于二维扁疤还需定义扁疤的宽度参数，不同于文献[7]中对不同扁疤宽度的考虑，本文通过以导致扁疤产生的钢轨的轨头形状(考虑轨底坡倾斜)(如图 7所示)来确定三维扁疤的宽度。三维扁疤的结构如图 8所示，即扁疤宽度参数与造成扁疤的钢轨轨头形状一一对应，此方法能够更好的贴合实际。

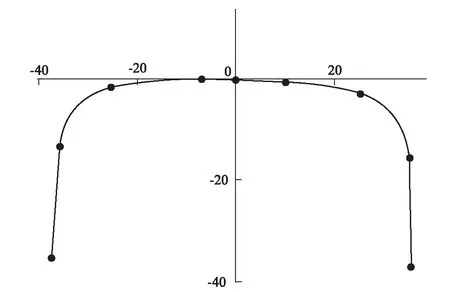
图7 导致扁疤产生的钢轨的轨头形状图(mm)

图8 三维扁疤结构示意图

根据上述的方法，结合车辆-轨道耦合动力学模型可完成车轮扁疤病害下车辆-轨道耦合振动仿真模型的建立。

3 仿真结果分析

3.1 车轮扁疤二维模型

由图5、图6可知，二维情况下的车轮扁疤冲击特征如冲击力等一定会在某冲击临界速度下发生突变，车轮从A点旋转过一定的角度(图中为φ/2)的时间为t1，车轮中心下落高度正好为扁疤弦长所对应的高度h的时间为t2。假设临界速度为vcr0，可知临界速度应该满足：t1=t2，可得：

(1)

式中：ω=v/R；

a——车轮下落加速度。

根据牛顿第二定律可得：

(2)

式中：m1和m2——车辆对应轮对一系簧上质量及簧下质量。

令t1=t2，可得：

(3)

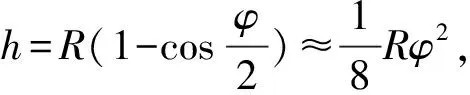
(4)

根据文献[8]可知较低速(v≤vcr0)时的冲击速度公式为：

(5)

式中：L——扁疤长度；

γ——车轮旋转惯量转换为往复惯量的系数。

可见，在较低速时冲击速度与扁疤长度L和行车速度成正比，与轮径R成反比。较高速度(v≤vcr0)时，冲击速度为：

(6)

由式(6)可知，在较高速时扁疤冲击速度与扁疤长度L成正比，与车速的关系较复杂。取γ=0.60，R=0.46 m，L=0.04 m，a=71.19 m/s2，保持其他变量为定值，分析高速铁路速度和扁疤长度变化时轮轨冲击速度和的变化情况，结果分别如图9、图10所示。

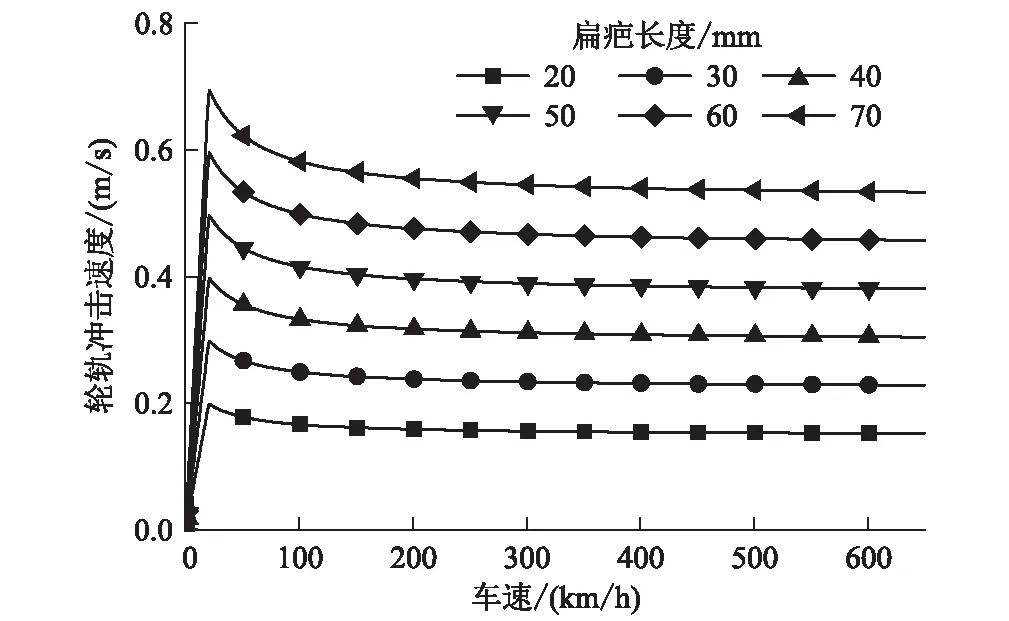
图9 轮轨冲击速度与车速关系图

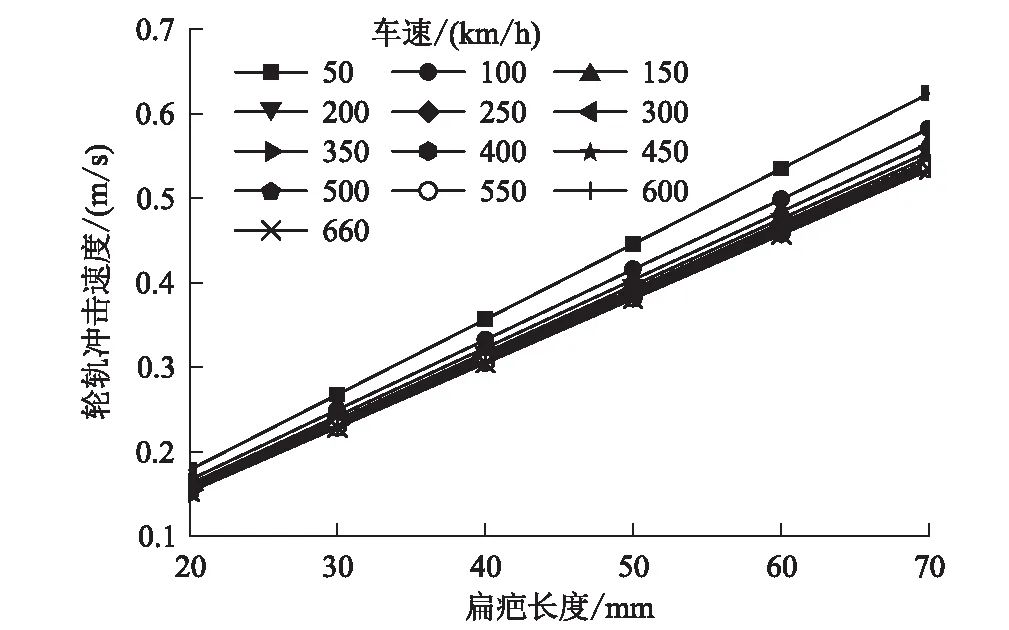
图10 轮轨冲击速度与扁疤长度关系图

由图9、图10可知，随着车速的增加，轮轨冲击速度先增大后减小，随后基本保持不变，产生最大冲击速度的临界车辆速度约为20 km/h，该临界速度即为前文所分析的车轮扁疤与轮轨接触姿态不同所造成的；随着车轮扁疤长度的增加，轮轨冲击速度基本呈线性增大，该二维冲击模型仿真结果能够在一定程度上反映轮轨冲击速度随扁疤长度及车速的变化情况，但为了满足更高速度的要求，以及更加贴近实际情况，本文将对车轮扁疤三维冲击模型下的轮轨冲击力进一步研究。

3.2 车轮扁疤三维模型

3.2.1 轮轨垂向力

为分析不同新扁疤长度下车辆以不同速度在线路上运行时的车轨冲击响应，选取60 kg钢轨，扁疤长度20～70 mm，步长10 mm，车速50～660 km/h，步长50 km/h等工况进行仿真，主要分析指标包括轮轨垂向力，轮轨垂向力与静轮重比值，扣件垂向力及扣件垂向力与扣件垂向静态力比值等。

车速400 km/h下，扁疤长度为40 mm、50 mm、60 mm、70 mm时的轮轨垂向力时间历程如图11所示。

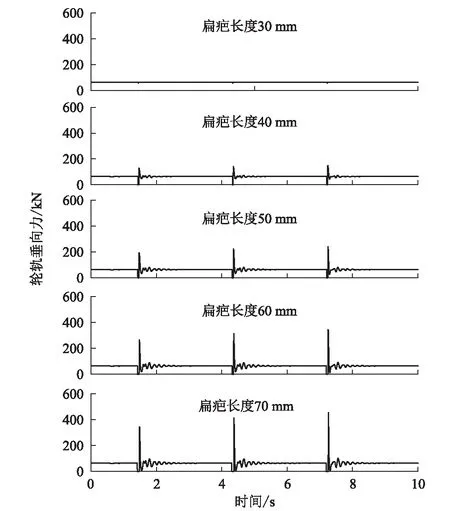
图11 车速400 km/h下不同扁疤长度下轮轨垂向力图

由图11可知，在扁疤作用下，轮轨垂向力出现冲击，之后逐渐收敛，并且随着车轮的滚动将会有周期性的冲击出现，且轮轨垂向力最大值都出现在第三个冲击的位置；随着扁疤长度的增加，轮轨垂向力冲击逐渐增大，在扁疤长度较小时如扁疤长度小于30 mm时，车轮一直都在轨道上，未出现轮轨脱离的情况，反之，当扁疤长度大于30 mm后车轮开始脱离钢轨，当扁疤长度为70 mm时，轮轨垂向力最大值约为456 kN。

选取不同车速、不同扁疤长度下轮轨垂向力统计最大值，如图12所示，其中图12(c)为低速时(即图12(b)框线部分)的局部放大图。

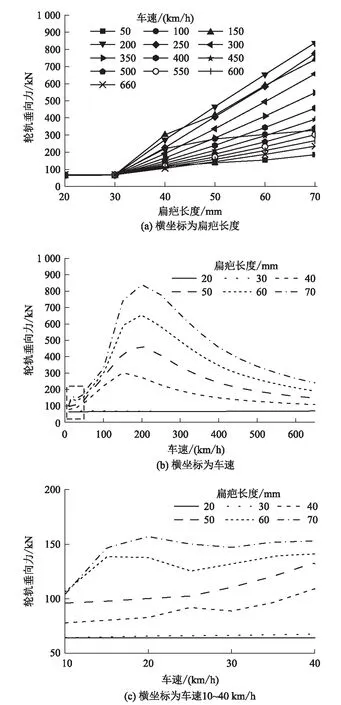
图12 轮轨垂向力随速度及扁疤长度变化情况图

由图12(a)可知，相同车速下，当扁疤长度大于30 mm 后，随着扁疤长度的增加，轮轨垂向力线性增大。由图12(b)、图12(c)可知，在相同扁疤长度下，随着车速的增加，轮轨垂向力先增大后减小，并且在车速10～50 km/h范围内存在一个峰值，这一点与扁疤二维模型仿真结果相对应，但是在速度较高情况下(150～200 km/h)还会出现一个峰值，且此峰值为轮轨垂向力最大值出现位置，这一现象是与二维模型仿真情况不相同的；当扁疤长度为70 mm时，轮轨垂向力最大值出现在车速200 km/h下，最大值约为838 kN，与文献[7]三维扁疤条件下的仿真计算结果相似。

选取不同车速、不同扁疤长度下轮轨垂向力与静轮重比值，如图13所示。

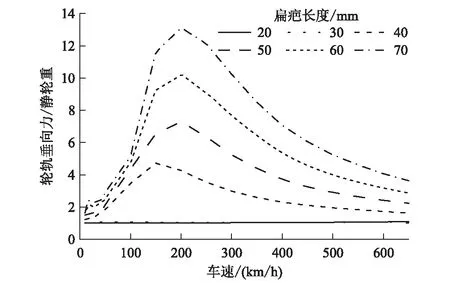
图13 轮轨垂向力/静轮重随速度及扁疤长度变化情况图

由图13可知，轮轨垂向力与静轮重比值变化规律与轮轨垂向力变化规律相似，当扁疤长度为70 mm时，轮轨垂向力/静轮重最大值约为11。

3.2.2 扣件垂向力

选取车速400 km/h下，扁疤长度为30 mm、40 mm、50 mm、60 mm、70 mm时的扣件垂向力时间历程，如图14所示。

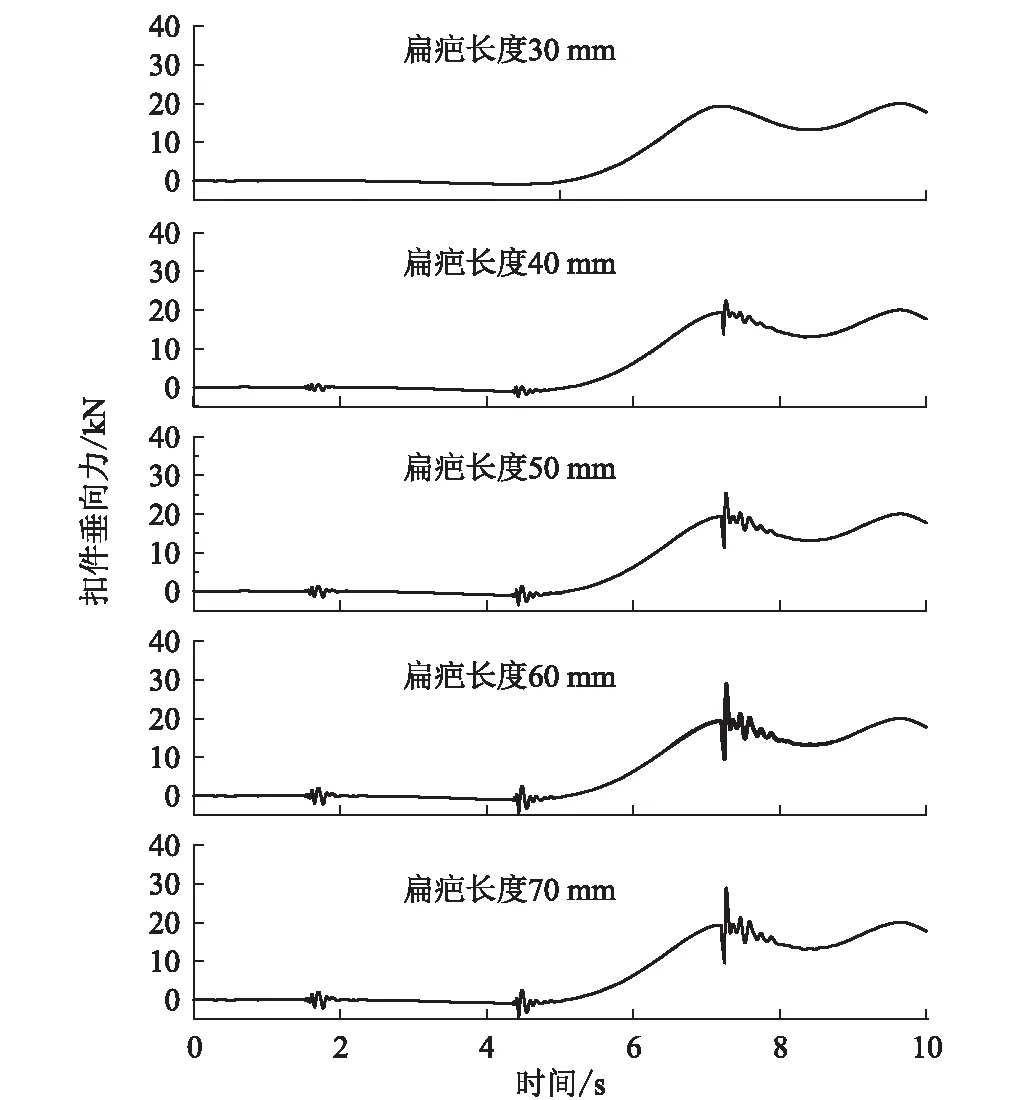
图14 车速400 km/h下不同扁疤长度下扣件垂向力图

由图14可知，在扁疤作用下，扣件垂向力出现冲击，并逐渐收敛，当车轮通过扣件且刚好与扁疤位置重合时(第三个冲击)的扣件垂向力最大，这也解释了车辆轮轨力最大值出现位置在第三个冲击。随着车轮的滚动将会有周期性的冲击出现；随着扁疤长度的增加，扣件垂向力逐渐增大，当扁疤长度为70 mm时，扣件垂向力最大值约为33 kN。

选取不同车速、不同扁疤长度下扣件垂向力统计最大值，如图15所示，其中图15(c)为低速时(即图15(b)框线部分)的局部放大图。

图15 扣件垂向力随速度及扁疤长度变化情况图

由图15(a)可知，相同车速下，当扁疤长度大于30 mm 后，随着扁疤长度的增加，扣件垂向力线性增大。由图15(b)及图15(c)可知，相同扁疤长度下，随着车速的增加，扣件垂向力先增大后减小，并且在车速 10～50 km/h范围内存在一个峰值，这一点与扁疤二维模型仿真结果相对应，但是在速度较高情况下(150～200 km/h)还会出现一个峰值，且此峰值为扣件垂向力最大值出现位置，这一现象是与二维模型仿真情况不相同的；当扁疤长度为70 mm时，扣件垂向力最大值出现在车速150 km/h下，最大值约为59 kN。

选取不同车速、不同扁疤长度下扣件垂向力与静态扣件力比值，如图16所示。

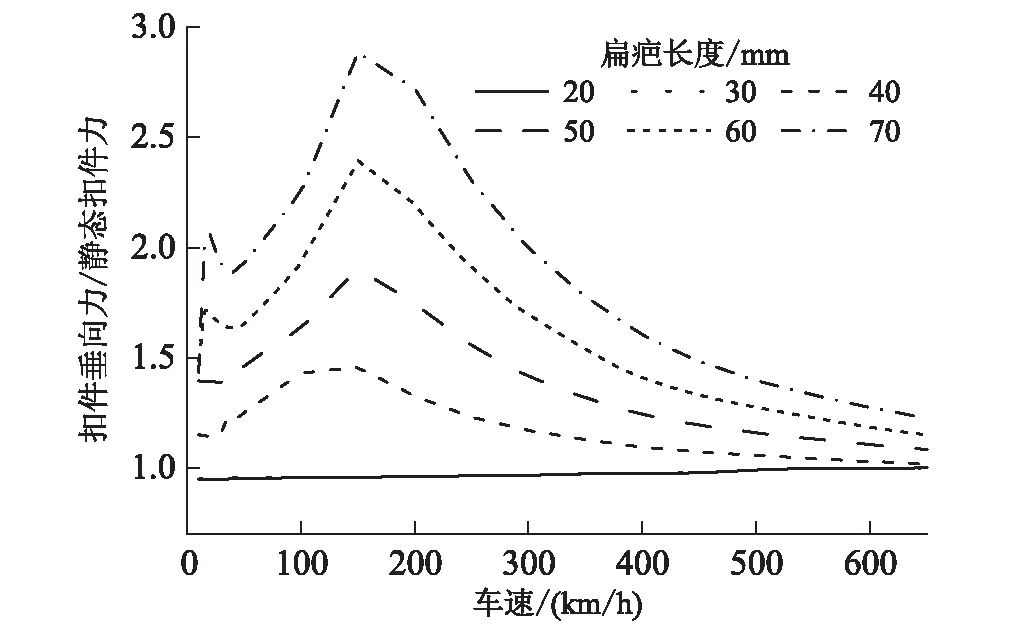
图16 扣件垂向力/静态扣件力随速度及扁疤长度变化情况图

由图16可知，扣件垂向力与静态扣件力比值变化规律与扣件垂向力变化规律相似，当扁疤长度为 70 mm 时，扣件垂向力/静态扣件力最大值约为2.8。

4 结论

本文采用多体动力学软件建立了详细考虑轨道扣件系统的车辆-轨道耦合模型，以造成车轮扁疤的钢轨形状为参考，对扁疤的三维形状进行了准确的模拟，分析了不同扁疤长度和不同车速下的车轨动力响应，得到的主要结论如下：

(1)对于二维扁疤模型，随着车速的增加，轮轨冲击速度先增大后减小，之后基本保持不变，产生最大冲击速度的临界车辆速度约为20 km/h，随着车轮扁疤长度的增加，轮轨冲击速度基本呈线性增大。

(2)对于三维扁疤模型，在扁疤作用下，轮轨垂向力及扣件垂向力出现冲击，并逐渐收敛，当车轮通过扣件且刚好与扁疤位置重合时(第三个冲击)的轮轨垂向力及扣件垂向力最大。

(3)对于三维扁疤模型，在相同车速下，随着扁疤长度的增加，轮轨垂向力及扣件垂向力线性增大；在相同扁疤长度下，随着车速的增加，轮轨垂向力及扣件垂向力先增大后减小，并且在车速10～50 km/h范围内存在一个峰值，这一峰值与扁疤二维模型仿真结果相对应，但是在速度较高情况下(150～200 km/h)还会出现一个峰值，且此峰值为轮轨垂向力及扣件垂向力最大值出现位置，当扁疤长度为70 mm时，轮轨垂向力最大值出现在车速200 km/h下，最大值约为 838 kN，扣件垂向力最大值出现在车速150 km/h，最大值约为59 kN。

(4)三维扁疤模型轮轨垂向力与静轮重比值及扣件垂向力与扣件静态力比值变化规律与轮轨垂向力及扣件垂向力变化规律相似，当扁疤长度为70 mm时，轮轨垂向力/静轮重最大值约为11，扣件垂向力/静态扣件力最大值约为2.8。

(5)在扁疤长度为70 mm时的轮轨垂向力最大值及轮轨垂向力与静轮重比值均明显较大，必须以标准、规范等文件对扁疤长度进行限制。