减振层刚度对减振型CRTSⅢ型板式无砟轨道振动响应影响

秦佳良 谢 毅 周冠南 周 涛 王建立 刘林芽 李秋义

(1.华东交通大学, 南昌 330013；2.中铁二院工程集团有限责任公司, 成都 610031；3.中国铁建大桥工程局集团有限公司， 天津 300300；4.中铁五局集团有限公司， 长沙 410007；5.隔而固(青岛)振动控制有限公司， 山东 青岛 266108；6.中铁第四勘察设计院集团有限公司， 武汉 430063)

近年来，随着我国高速铁路的快速发展，我国自主研发的CRTSⅢ型板式无砟轨道由于高平顺、高稳定性和少维修等诸多优点，在铁路上广泛应用。

对于车辆-无砟轨道结构的振动问题，国内外学者进行了大量的研究。Guigou-Carter等[1]人开发了一种二维的板式轨道系统预测模型，轨道系统由钢轨、轨道板和混凝土底座板组成，分析了轨枕垫的动态刚度对轨道系统隔振效果的影响；Khajehdazfuly[2]建立了高速列车-CRTSⅡ板式无砟轨道垂向数值模型，研究了谐波不平顺下轨道垫板刚度对轮轨力的影响；翟婉明等[3]运用车辆-轨道耦合动力学理论，建立了高速列车与板式轨道相互作用的垂向动力学模型，针对日本新干线板式轨道，分析了CA砂浆的刚度和阻尼变化对轨道结构动力特性的影响；蔡成标[4]建立了路基上无砟轨道空间耦合动力学模型，考虑了垂、横向运动，研究了遂渝线无砟轨道综合试验段路基上板式轨道的动力学特性；向俊等[5-6]基于弹性系统动力学总势能不变值原理，提出了一种横向有限条与无砟轨道板段单元分析模型，针对CRTSⅠ型板式轨道研究了车速和轨道高低不平顺对系统竖向振动响应的影响；雷晓燕等[7-8]提出了一种新型板式轨道单元，建立了车辆-板式轨道-路基耦合系统的动力学模型，针对CRTS Ⅱ型板式无砟轨道研究了板式轨道结构及过渡段的动力学行为，评估了列车速度和轨道刚度对轨道振动的影响。对于CRTSⅢ型板式无砟轨道，相关研究主要集中在结构的设计以及施工方面，而对于CRTSⅢ型板式无砟轨道动力学的研究还较少。

基于以上研究成果，本文采用有限元法，建立了列车-减振型CRTSⅢ板式轨道耦合系统竖向动力响应，以中国高速铁路轨道不平顺谱作为激励源，分析列车荷载作用下减振型CRTSⅢ板式轨道的动力特性，并对减振层刚度变化对轨道结构振动响应的影响进行了研究。

1 车辆-轨道耦合动力学模型

1.1 基本假设

采用有限元法建立车辆-CRTS Ⅲ型板轨道耦合系统竖向振动模型，应满足以下假设：

(1)车辆系统简化为附有二系弹簧阻尼的整车模型，轨道系统简化为三层板式轨道单元模型，轮轨之间采用非线性弹性接触。

(2)钢轨视为离散点支承的二维Euler梁，扣件垫板的弹性系数和阻尼系数分别用Kp和Cp表示。

(3)轨道板和自密实混凝土视为连续粘弹性支承的二维梁单元，减振层的弹性系数和阻尼系数分别用Km和Cm。

(4)底座板也视为连续粘弹性支承的二维梁单元，底座板下部基础支承的弹性系数和阻尼系数分别用Ki和Ci。

1.2 CRTSⅢ型板轨道单元模型

路基上CRTS Ⅲ型板式无砟轨道系统结构如图1所示，基于上述的假设可以得到建立的三层轨道单元模型，如图2所示。

图1 路基上CRTS Ⅲ型板式轨道图

图2 三层梁有限元模型图

图2中，v1和v4表示钢轨的竖向位移；θ1和θ4表示钢轨的转角；v2和v5表示轨道板+自密实混凝土的竖向位移；θ2和θ5表示轨道板+自密实混凝土的转角；v3和v6表示底座板的竖向位移；θ3和θ6表示底座板的转角。

定义CRTS Ⅲ型板轨道单元节点位移向量为：

(1)

板式无砟轨道单元的刚度矩阵可表示为：

(2)

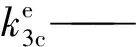
板式无砟轨道单元的阻尼矩阵可表示为：

(3)

板式无砟轨道单元的质量矩阵可表示为：

(4)

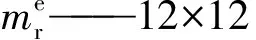
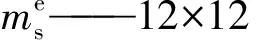
无砟轨道单元等效节点荷载向量为：

(5)

其中：Fi(i=1～4)——轮轨接触力，可由轮轨接触关系求得。

根据上述轨道单元模型，利用有限元“对号入座法”组集轨道单元刚度、阻尼和质量矩阵以及荷载向量，即可得到轨道系统振动方程为：

(6)

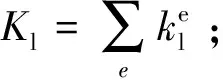
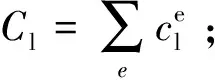
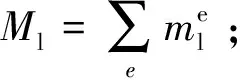
1.3 车辆单元模型

车辆系统简化为一个附有二系悬挂弹簧阻尼的整车模型，由1个车体、2个转向架和4个轮对组成。考虑了车体的沉浮和点头运动，前后构架的沉浮和点头运动，以及4个轮对的垂向振动共10个自由度。定义车辆单元节点位移向量为：

(7)

其中：vc——车体沉浮振动的竖向位移；

θc——车体点头振动的角位移；

vti和θti(i=1,2)——分别为前、后转向架沉浮振动的竖向位移和点头振动的角位移；

vwi(i=1,2,3,4)——第i个车轮的竖向位移。

由Hamilton原理，可得到车辆系统振动方程为：

(8)

Mv——车辆系统的质量；

Kv——车辆系统的刚度；

Cv——车辆系统的阻尼矩阵。这些矩阵的显式表达式参见文献[9]。

Qv为车辆系统的广义力向量：

(9)

式中：g——重力加速度；

Fi(i=1～4)——轮轨接触力，可用轮轨非线性Hertz接触公式求得。

2 耦合方程数值求解

(10)

(11)

(12)

3 减振层刚度对耦合系统动力特性影响

3.1 计算参数

仿真分析中，车辆选用高速动车CRH3，具体参数如表1所示，轨道选择减振型CRTSⅢ板式无砟轨道，其参数如表2所示。

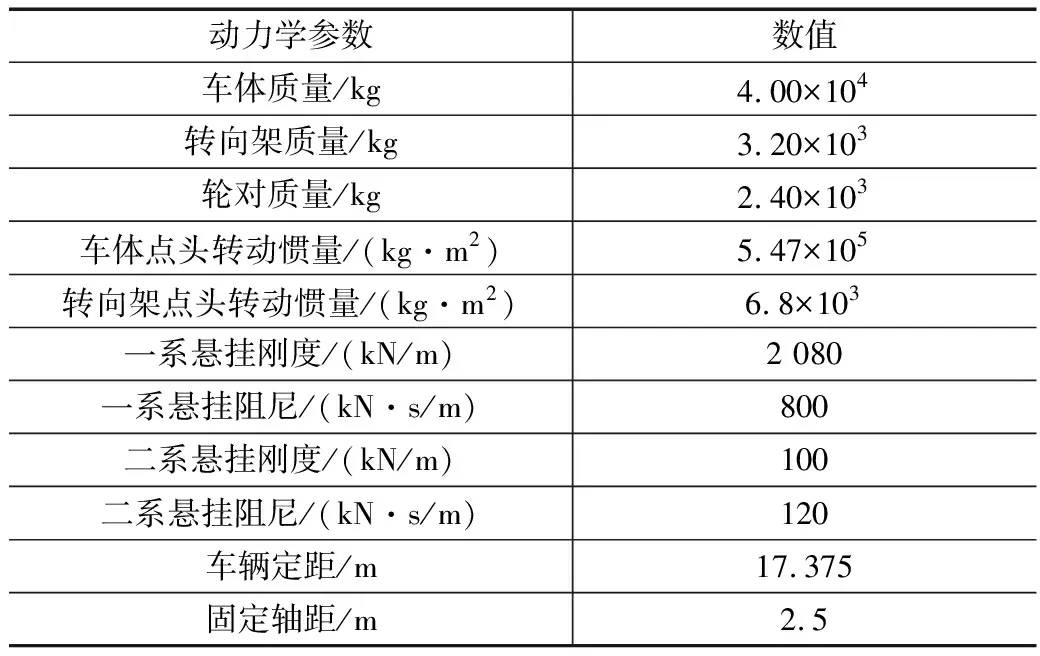
表1 CRH3高速客车的动力学参数表

表2 减振型CRTSⅢ板式轨道参数表

3.2 动力特性参数分析

减振型CRTSⅢ板式无砟轨道的特点是在自密实混凝土和底座板之间铺设1层橡胶减振垫层。为研究不同减振层刚度和阻尼变化对轨道结构变形的影响，本文分别取减振层刚度km为100 kN/mm、400 kN/mm、700 kN/mm、1 000 kN/mm。轨道不平顺类型选取我国的高速铁路无砟轨道不平顺谱，计算减振层刚度变化对车辆、轨道系统振动的影响。

减振层刚度变化对车体和轮轨力影响的对比如图3所示。从图3可以看出，随着减振层刚度的增大，车体加速度有所减小但变化不明显，当减振层刚度从100 kN/mm增加到 1 000 kN/mm，车体加速度减小 0.001 04 m/s2，影响较小；轮轨力也有所减小，当减振层刚度从100 kN/mm增加到 1 000 kN/mm，车体加速度减小 0.001 04 m/s2，影响较小。

图3 减振层刚度对车体和轮轨力的影响图

减振层刚度变化对钢轨动力特性影响的对比如图4所示。从图4可以明显看出，随着减振层刚度的增大，钢轨位移整体有所减小，当减振层刚度为100 kN/mm时，钢轨最大位移为1.21 mm；当减振层刚度变为400 kN/mm、700 kN/mm和 1 000 kN/mm时，钢轨最大位移为0.98 mm、0.94 mm和0.93 mm，钢轨最大位移降幅为22.93%、3.64%、1.48%，降低的速率随着减振层刚度的增大而减小。随着减振层刚度的增大，钢轨加速度也有所减小，当减振层刚度为100 kN/mm时，钢轨最大加速度为8.50 m/s2；当减振层刚度变为400 kN/mm、700 kN/mm和 1 000 kN/mm时，钢轨最大加速度为8.44 m/s2、8.35 m/s2和8.28 m/s2，钢轨加速度降幅为0.72%、1.11%、0.79%。

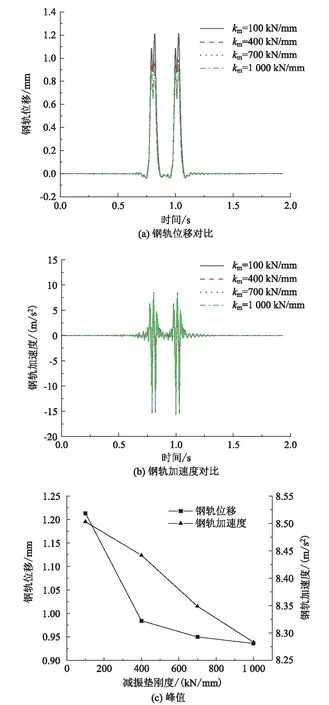
图4 减振层刚度对钢轨动力特性的影响图

减振层刚度变化对轨道板动力特性影响的对比如图5所示。从图5可以明显看出，随着减振层刚度的增大，轨道板位移整体减小，当减振层刚度为100 kN/mm时，轨道板最大位移为0.789 mm；当减振层刚度变为400 kN/mm、700 kN/mm和 1 000 kN/mm时，轨道板最大位移为0.588 mm、0.556 mm和0.5 44 mm，轨道板最大位移降幅为34.36%、5.58%、2.20%，降低的速率有所减缓。随着减振层刚度的增大，轨道板加速度也有所减小，当减振层刚度为100 kN/mm时，轨道板最大加速度为3.01 m/s2；当减振层刚度变为400 kN/mm、700 kN/mm和 1 000 kN/mm时，钢轨最大加速度为2.46 m/s2、2.23 m/s2和2.10 m/s2，轨道板加速度降幅为21.95%、10.22%、6.35%。

图5 减振层刚度对轨道板动力特性的影响图

减振层刚度变化底座板动力特性影响的对比如图6所示。从图6可以看出，随着减振层刚度的增大，底座板位移不断增大但变化较小，减振层刚度从100 kN/mm增加到 1 000 kN/mm，底座板位移增大 0.001 09 mm，影响较小。底座板加速度随着减振层刚度的增大也不断增大，底座板的加速度增幅为15.08%、4.03%、0.69%。

图6 减振层刚度对底座板动力特性的影响图

4 结论

本文基于有限元理论，建立了列车-CRTS Ⅲ型减振板式轨道耦合动力学模型，分析了不同减振层刚度对轨道结构动力特性的影响[10]，主要结论如下：

(1)减振层刚度的变化对车体的振动影响较小，对钢轨、轨道板和底座板的振动影响较大。

(2)减振层刚度的增大能有效的降低减振层以上结构的振动，引起下部结构的剧烈振动。

(3)从设计的角度来看，减振层刚度不宜设置的太大，否则将削弱板式轨道的弹性，不利于轨道结构减振；同时考虑减振层上部和下部结构的动力效应，建议减振层刚度应在 400～700 kN/mm。