带负载观测器的永磁同步电机滑模无差拍控制

祖 冉，李 敏，黄妍慧，何 龙

(1.安徽机电职业技术学院 汽车与轨道学院，安徽 芜湖 241000；2.中科院 福建物质结构研究所，福建 福州 350000)

0 引 言

永磁同步电动机具有结构简单、效率高、功率密度高、调速范围宽等特点.它已被广泛应用于工业伺服机器人、航空航天等高控制精度和高控制可靠性场合，并逐渐成为中小型交流伺服驱动器的主流.为了提升永磁同步电机控制系统的响应速度和鲁棒性，需对速度外环和电流内环作进一步的改进.

当前，电流环的控制策略主要包括滞环控制、比例积分(PI)控制和电流预测控制.滞环控制方法简单，不依赖于电机参数，具有良好的鲁棒性，可以加快动态调节速度，抑制回路中的干扰[1].然而，随着逆变器开关频率的变化，滞环控制的输出电流波形波动较大，会带来系统噪声.PI调节器具有结构简单、稳定可靠等优点，通过增大调节器的增益可以改善系统的动态性能，但过大的增益会影响系统的稳定性，带来超调和噪声.在实际应用中，很难考虑响应的快速性和稳定性[2].电流预测控制是研究热点，相比于传统矢量控制，预测电流具有更高的动态和稳态响应.然而，预测控制算法复杂，运算资源所需较多，采样的延时也会对预测精度产生一定的影响[3].

速度环控制策略主要有PI控制、滑模控制等.速度PI控制器结构简单，易于实现，适合绝大多数应用场合.但当系统出现较大的干扰时，控制精度无法被保证.滑模控制的优点是不需要对系统进行精确观测，控制律的整定方法简单，系统在扰动发生时迅速响应和调整[4].高阶滑模和快速终端滑模是研究的热点领域，通常外环滑模还与观测器技术相结合，用来进一步减少外界干扰对控制系统的影响[5].

在电流预测的基础上，本文提出了基于两拍延时补偿的无差拍电流预测控制策略.该策略能降低传统预测控制的复杂度，减少对芯片资源的消耗，易于实现.同时，也能缩小采样、硬件转换所带来的延时，改善了电流回路的动态响应.对速度环来说，在传统滑模的基础上，为了适应数字芯片控制模式，设计了离散积分滑模控制器.该控制器不仅减小了系统的稳态误差，而且使系统具有全局鲁棒性，指数趋近律的结构简单明了.通过调整趋近律的参数，可以保证滑模的动态品质.为了降低抖振对控制系统精度的影响，本文还设计了扰动滑模观测器，将观测到的负载变化反馈到速度滑模，有效地抑制了速度滑模的抖动，提高了控制系统的抗干扰能力.

本文在永磁同步电动机矢量控制方法的基础上，将两拍延时补偿的无差拍预测控制引入电流环，将带前馈补偿的改进滑模引入速度环，实现了系统的双闭环控制.实验结果表明，两种控制方式的组合具有较高的动态性能和较强的鲁棒性.

1 永磁同步电机模型

为了便于分析，假设三相定子绕组对称，空间角互差为120°，磁场沿气隙呈正弦分布；不考虑涡流和磁滞损耗；定子绕组和转子的永磁体产生的磁动势为正弦波；永磁体和转子为无阻尼绕组.

旋转坐标系下永磁同步电动机定子电压方程可简化为

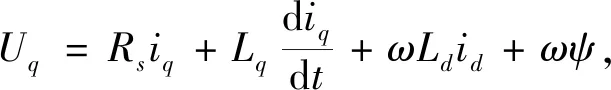
(1)

式中：id，iq，Ud，Uq为定子电流和电压在d、q轴上的分量；R为定子电阻；Ld，Lq为d、q轴电感；对于表面安装式永磁同步电动机(本文使用的表面式永磁同步电动机)，假设Ld=Lq=Ls；ω是电机角速度；ψ是永磁体磁链.

矢量控制系统分为电流内环和速度外环，采用PI控制方法.d轴一般采用id=0的控制策略.

2 控制策略

本文在传统矢量控制的基础上，采用了一种更为快速的控制方式.电流环采用两拍延时补偿的无差拍预测控制策略，具有良好的电流动态响应和系统响应速度.速度环采用增量积分滑模控制，具有良好的抗干扰能力和鲁棒性.图1 为结合无差拍算法和滑模算法的控制策略框图.

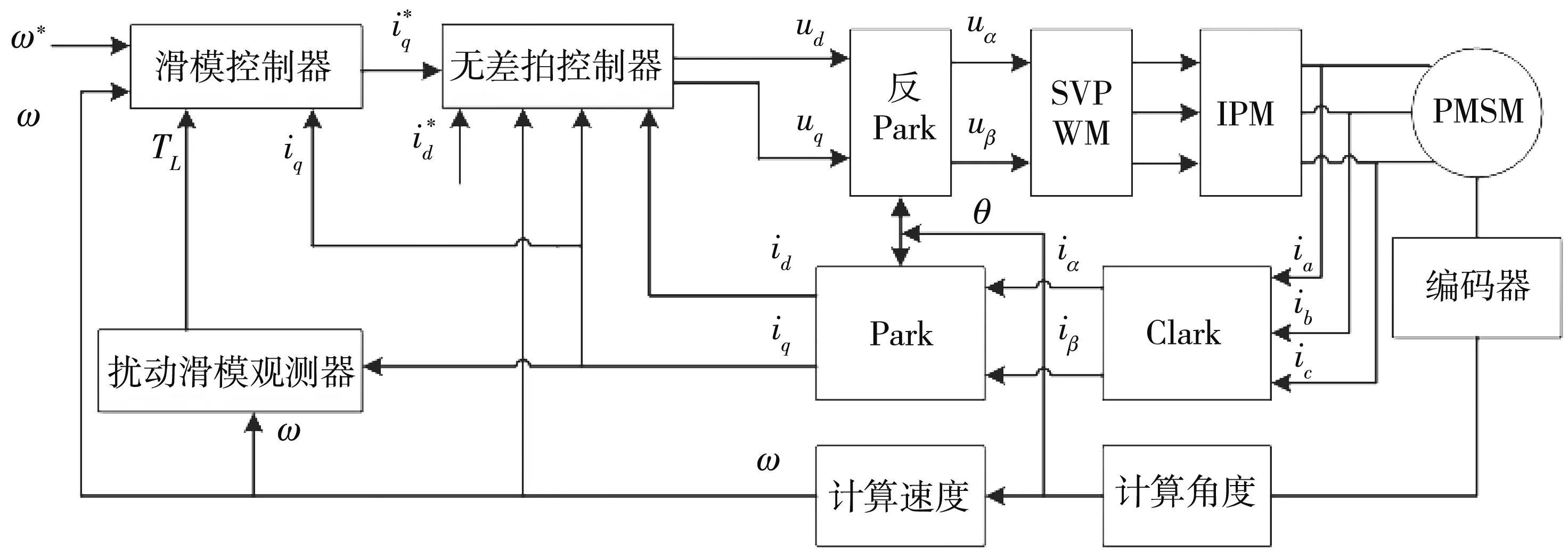
图1 控制系统框图Fig.1 Block diagram of control system

3 速度滑模控制器

3.1 积分滑模

首先选择滑模面，假设给定速度ω*与实际速度ω之差为

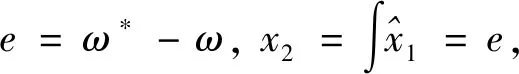
(2)

则系统的状态变量可以表示为

(3)

x1和x2的导数分别为

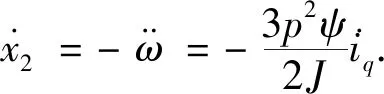
(4)

滑模变结构涉及加速度的计算.常规的计算方法会使系统的精度和动态性能变差.因此，本文选择积分滑模控制器，只需要计算速度.

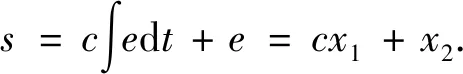
(5)

公式中积分项的存在减小了速度控制的稳态误差.

对式(5)求导可以得到

(6)

为了提高控制器的动态性能，采用指数趋近律设计控制器.指数趋近定律的表达式为

(7)

在式(7)中，令s>0，则

(8)

求解微分方程

(9)

可以看出，在指数趋近律中，当t足够大时，趋近速度非常快.

当s>0，s(t)=0时，有

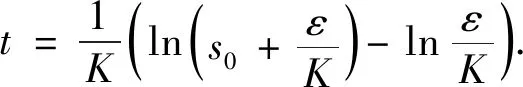
(10)

增加ε和K将加快趋近运动，却降低了到达速度.然而，过大的ε和K会导致系统抖振程度的增加.因此，合理调整和选择这两个系数，对于保证系统有效地削弱抖振，加速系统的趋近运动非常重要.

根据式(6)和(7)可得，控制器的输出为

(11)

3.2 离散积分滑模控制器

离散积分滑模控制器更适合于数字芯片控制，故有必要对滑模进行离散化.将式(3)离散化为

x1(k+1)=x1(k)-T(hiq(k)-HTL(k)),

x2(k+1)=x2(k)-D(iq(k+1)-iq(k)),

(12)

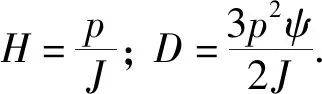
离散滑模面可以表示为

s(k)=x1(k)+cx2(k).

(13)

根据可达性条件，当采样时间很短时，满足

(s(k+1)-s(k))sgn(s(k))<0,

(s(k+1)+s(k))sgn(s(k))>0.

(14)

离散趋近律可以表示为

s(k+1)=(1-qT)s(k)-εTsgn(s(k)).

(15)

根据上面的推导，可以得到

(H+TcH)TL(k)-THiq-cω(k)+cω*(k)].

(16)

3.3 负载扰动滑模观测器

积分滑模不需要加速度信号，易于实现.但是积分控制器具有积分环节，会导致系统的响应滞后，容易引起积分项饱和，也会对系统的控制性能产生负面影响[6].在构造积分滑模控制器时，控制器中加入了系统的不确定性.因此，外部干扰的实时观测可以保证积分滑模控制器的控制精度.为此，提出了一种基于负载扰动的滑模观测器，并将观测器的输出反馈给速度滑模.

滑动模态利用开关的不连续性来抑制外界对系统的干扰.当控制负载发生变化时，滑模的切换增益会增加，但这会引起系统更大的抖振，也会引起转速的瞬时波动，降低系统的控制性能.为了在负载变化时保持良好的控制性能[7-8]，设计了以负载为主要观测器的滑模观测器.

永磁同步电机的转矩方程为

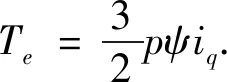
(17)

永磁同步电机的运动方程为

(18)

根据式(17)和式(18)所示的永磁同步电机动能方程，以负载转矩为状态扰动，可得状态方程

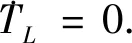
(19)

将式(19)离散化，得

(20)

当控制周期非常短时，可以认为负载扭矩在几个控制循环中是一个恒定值，因此TL=0.在式(19) 的基础上，以永磁同步电机的负载扰动和角速度为观测变量，构造了滑模观测器.

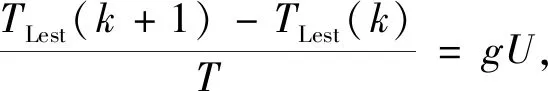
(21)

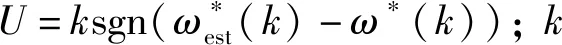
3.4 负载滑模观测器结构

根据前面的推导和证明可得，速度滑模控制器的输出电流可以通过将观测到的负载转矩反馈给速度滑模控制器进行前馈补偿得到.

(H+TcH)TLest(k)-THiq(k)-cω(k)+cω*(k)].

(22)

根据式(22)选择合适的反馈增益g和滑模增益k，可以保证滑模观测器的稳定性，准确观测负载转矩.观测器结构如图2 所示.

图2 负载转矩观测器的结构图Fig.2 Structure diagram of load torque observer

4 无差拍电流预测控制

无差拍电流预测的基本思路是根据电机d、q轴的离散数学模型，以及电机在当前时刻的实际采样值和当前时刻的给定值，预测电机在下一时刻的控制电压.逆变器的数学模型可描述为1/(0.5Ts+1).由于采样时间T很小，在频域内，逆变器只影响电流回路的高频段，而对中低频段的影响很小，可以忽略不计.电流环的响应速度一般只在中频频段，所以，在研究电流环的响应速度时，只考虑电动机而不考虑逆变器环节.在两相旋转坐标系下，永磁同步电机的d、q轴电压方程为

(23)

将式(23)改写为向量形式的状态空间函数

(24)

方程(24)在连续域中的通解为

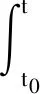
D(τ)]dt.

(25)

将式(25)离散化，并假设控制系统的输入变量u在采样时间T非常小的周期内几乎不变.变量D是反电动势的影响，但它相对于电流变化较缓慢，可以认为它在一段时间内保持不变.因此，可获得离散解为

X(k+1)=MX(k)+A-1(M-I)(Bu(k)+D(k)),

(26)

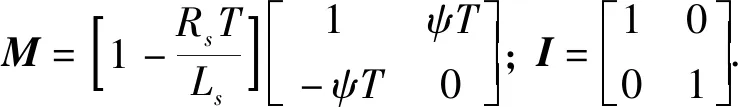
因此，电流的预测模型可以写成

X(k+1)=C(k)X(k)+G(k)u(k)+H(k).

(27)

根据式(27)，电压方程可以写为

u(k)=G-1{X(k+1)-C(k)X(k)-H(k)}=

G-1{i(k+1)-C(k)i(k)-H(k)}.

(28)

无差拍电流预测控制通过电流采样值和给定值来预测未来的期望值，然后计算出电压参考值.理想的控制方式是用kT时间对电机电流进行采样，计算PWM占空比，同时更新占空比.在实际系统中，首先检测当前值id(k)、iq(k)和电机角速度ω.这些值反馈至速度环，即电流的给定值idref(k)，iqref(k)，再由速度环计算.然后，电流环用于计算要施加的电压.在此过程中，在kT时间对电机电流进行采样，并在时间间隔kT和(k+1)T内计算PWM的占空比信号.占空比信号直到(k+1)T时才更新.逆变器还需要另一个周期将占空比信号转换为电机侧的电压信号.因此，控制系统的总延迟为当前采样周期的2倍，即2T[9-10].式(27)可以写为

i(k+1)=Ci(k)+Gu(k)+H.

(29)

如图3 所示，(k+1)T时的电流应在kT时的采样周期内计算.电机的给定电压是在kT时计算的电压，为u(k+1).因此，(k+2)T时间采样的电流为

图3 带延迟补偿的无差拍电流控制框图Fig.3 DB block diagram with delay compensation

i(k+2)=Ci(k+1)+Gu(k+1)+H.

(30)

由式(30)可知，电流矢量i(k+2)由i(k+1)和u(k+1)确定，i(k+1)由i(k)和u(k)共同确定.因此，通过引入公式(30)，可以得到i(k+2)的另一个表达式，为

i(k+2)=C(Ci(k)+Gu(k)+H)+

Gu(k+1)+H.

(31)

由于电机的时间常数远大于采样周期，转子角速度在几个周期内可以被视为不变[11-12].假设电机的模型参数为常数，(k+1)时的预测电压为

u(k+1)=G-1(i(k+2)-C(Ci(k)+

Gu(k)+H)-H).

(32)

假设两拍的延迟得到完全补偿，即(k+2)时的电流值已跟踪到给定值，则i(k+2)的值可由k时的参考电流代替.

u(k+1)=G-1(iref-C(Ci(k)+Gu(k)+H)-H).

(33)

5 实验验证

图4 是1 kW永磁同步电机的控制系统.开关器件采用三菱PM100RL1A120内PM(IPM)模块，为满足100 μs电流控制周期，PWM开关选择1 ms速率控制周期和2 μs死区时间.主运算单元使用TMS320F28335模块.IPM由直流电源供电.为了将控制器与选通电路的噪声隔离，使用了光耦电路.表1 是实验电机的基本参数.

图4 实验平台Fig.4 Experimental platform

表1 电机参数Tab.1 Motor parameters

为验证滑模无差拍的空载启动性能，给定的实验条件为空载启动，转速为1 000 r/min.图5 为空载起动速度、三相电流、d轴电流和q轴电流曲线.从图中可以看出，启动响应较快，约为0.1 s，速度超调小，约为10 r/min.三相电流毛刺小，稳态接近为0.d轴电流启动时有波动，0.2 s 后稳定为0.q轴电流启动时有短暂的脉冲，持续时间约为0.1 s，稳态接近为0.

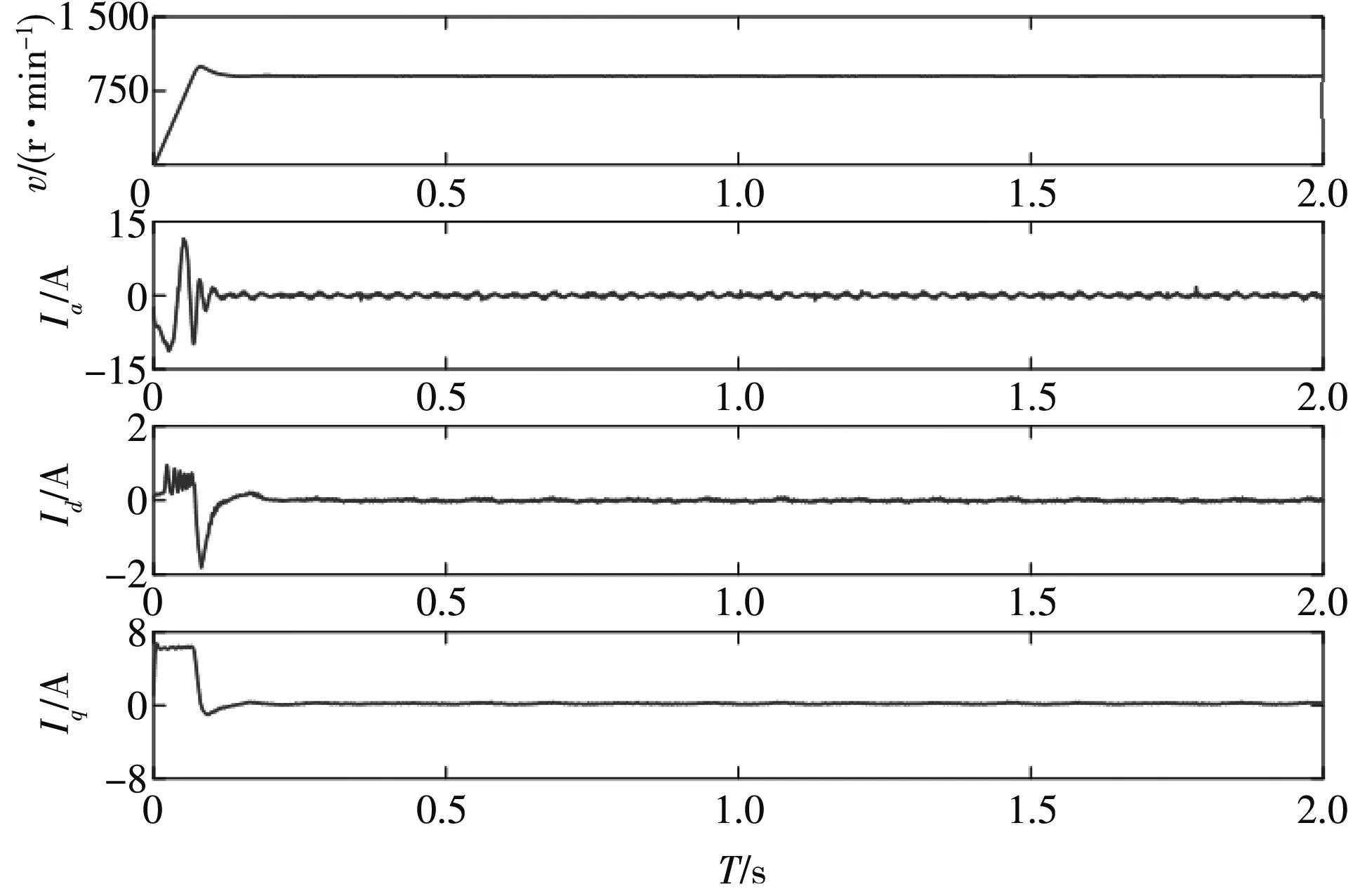
图5 空载启动特性Fig.5 No load starting characteristics

为验证滑模无差拍控制加载启动的性能,给定的实验条件为：转速为1 000 r/min，初始负载为 3 N·m.图6 是由滑模无差拍控制的加载开始时的转速、三相电流和d、q轴电流波形.从图中可以看出，启动响应较快，约为0.15 s，速度超调小，约为8 r/min.三相电流毛刺小，无畸变，呈现较好的正弦波.d轴电流稳态时有较小的纹波，整体为0.q轴电流的响应时间约为0.01 s，稳态电流较为平稳.

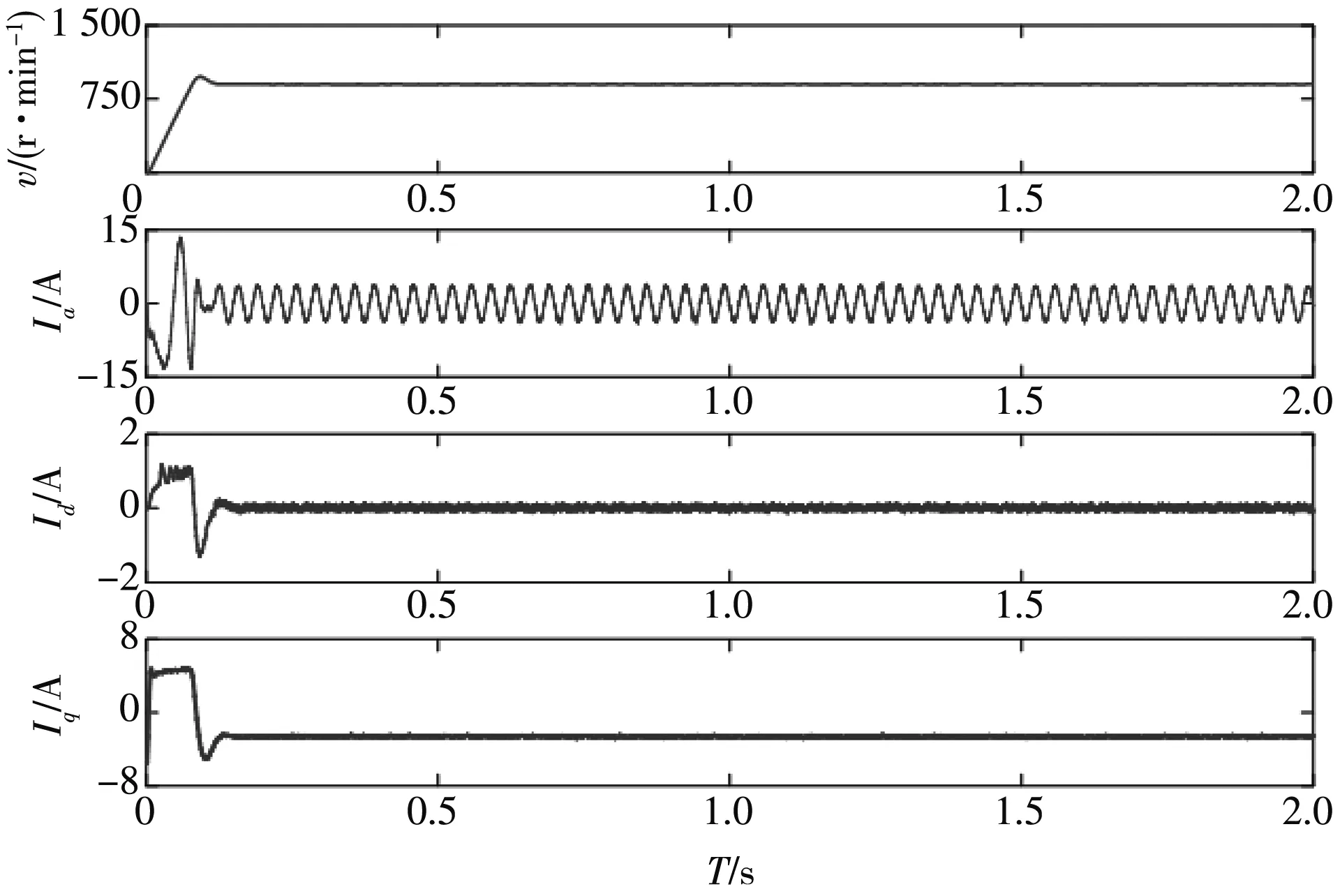
图6 带载启动特性Fig.6 On load starting characteristics

为验证滑模无差拍控制的加速特性，给定的实验条件为：负载为3 N·m，转速从500 r/min增加到700 r/min.实验结果如图7 所示.转速响应迅速，响应时间约为0.07 s，稳态误差为0.三相电流动态变化幅度小，稳态为理想正弦波.d轴电流动态有较小波动，0.01 s后稳定为0.q轴电流有短暂的脉冲变化，时间约为0.1 s，稳态电流误差为0.

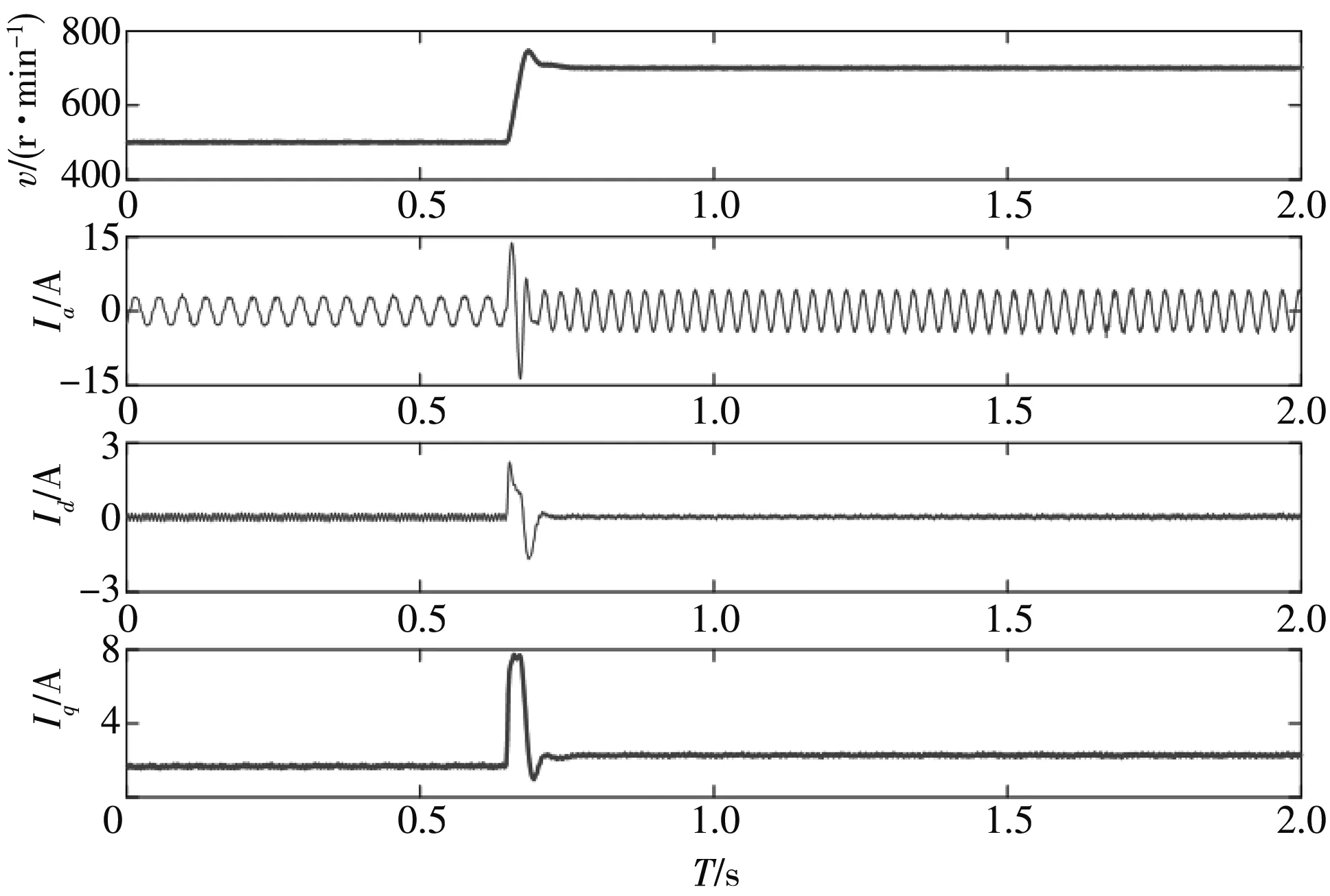
图7 加速特性Fig.7 Acceleration characteristics

为验证加载特性，给定的实验条件为转速 600 r/min，负载为3 N·m，某时刻突加负载 2 N·m.实验结果如图8 所示.可以看出，负载突变时，转速波动幅度为10 r/min，经过0.1 s调节，恢复到给定值.A相电流过渡平稳，波形近似为正弦波.q轴电流响应较快，响应时间约为0.09 s，稳态电流波动较小.

图8 加载特性Fig.8 Loading characteristics

为验证正反转特性，给定的实验条件为：负载3 N·m，转速从700 r/min变化到-700 r/min，实验结果如图9 所示.可以看出，转速变化平稳，响应较快，过渡时间为0.15 s.三相电流变化平缓，经过短暂的波动，便恢复到稳态.d轴电流保持为0，动态变化幅度较小.q轴电流响应迅速，响应时间约为0.05 s，稳态电流平稳，无振荡.

图9 正反转特性Fig.9 Forward and reverse characteristics

从实验结果可以看出，滑模无差拍控制策略不仅具有快速的动态响应能力，而且具有较强的鲁棒性，证明了滑模无差拍控制算法的有效性.

6 结 论

在传统矢量控制的基础上，采用带负载观测器的滑模控制策略代替速度外环的PI控制器，采用无差拍电流预测控制代替电流内环的PI控制器.实验结果表明，该组合控制策略不仅使整个控制系统具有抗外部干扰的能力，而且使控制系统具有无差拍电流预测控制的快速响应能力.实验证明，基于前馈补偿的永磁同步电机滑模无差拍控制具有很强的鲁棒性和良好的动态响应能力.