含水率对微钻阻力仪钻针阻力的影响
姚建峰,雷相东,王雪峰,符利勇,郑一力,郭旭展,,段光爽,宋新宇
(1.信阳师范学院 a.计算机与信息技术学院;b.数学与统计学院,河南 信阳 464000;2.中国林业科学研究院 资源信息研究所,北京 100091;3.北京林业大学 工学院,北京 100083)
微钻阻力仪(又称针刺仪,阻抗仪)是使用电机控制钻针匀速钻入树木并实时记录钻针阻力的一种精密测量仪器[1]。钻针阻力使用电机所消耗的能量间接表示,当钻针进给速度和旋转速度由不同的电机控制时,钻针进给方向上的阻力由控制钻针进给速度的电机消耗的能量间接表示,钻针旋转方向上的钻针阻力由控制钻针旋转速度的电机消耗的能量间接表示[1-2]。但有部分仪器只给出旋转方向上的阻力,没有给出钻针进给方向上的阻力。当钻针进给速度和旋转速度由一个电机控制时,钻针阻力即为该电机所消耗的能量。因此,在没有明确说明钻针阻力的方向时,钻针阻力可能是钻针旋转方向上的阻力,也可能是钻针旋转方向和进给方向上的阻力和。钻针阻力主要受钻针针头切削木材密度的影响,木材密度越大,破坏木材组织结构所需的能量越大,钻针阻力越大[3-4]。由于钻针阻力采样间距很小,通用版一般是0.1 mm,科学版一般是0.01 mm。因此,根据钻针阻力可以获取钻针路径上微小区域的木材密度。当钻针沿径向方向钻入树木时,钻针针头交替地钻过树木年轮的晚材部分和早材部分,钻针阻力呈波峰-波谷规律变化,因此,根据钻针阻力曲线图可获取树木年轮信息[5-6]。当钻针钻入腐烂区域、裂缝、空洞时,钻针阻力明显下降,因此,根据钻针阻力可检测木材内部的缺陷情况[7]。微钻阻力仪钻针针头宽度仅3 mm,对被测对象损伤较小,为测量木材密度[8-10]、树木年轮[11]、木材缺陷[12-13]等方面提供了一种微损测量方法。
由于木材的力学性质指标参数不仅受木材密度的影响,而且还受木材含水率的影响[14-15],因此,钻针阻力可能受木材含水率的影响。Lin 等[16]把3 棵22年生的秃杉Taiwania cryptomerioides的木材按2 cm×1 cm×18 cm 规格加工成测试件,首先在木材处于饱和含水率状态下取样各测试件的钻针阻力,然后每当测试件质量减小5~8 g时,重新取样各测试件的钻针阻力,直到测试件处于自然风干状态为止,研究发现钻针阻力R与木材含水率MC 正相关,具体回归模型是:R=0.68MC+312.4(R2=0.31,F=356.7)。李华等[17]把落叶松和云杉的古建材和新鲜材加工成10 cm×10 cm×5 cm 试件,通过恒温恒湿箱和干燥箱将试件含水率分别控制在4%、12%、20%和28%,在不同含水率下使用微钻阻力仪对每个试件进行1 次径向取样和2 次弦向取样,每组试验重复3 次,取3 次测量阻力的平均值为最终测量结果,研究发现:当木材含水率在5%~20%范围内,钻针阻力与含水率负相关;当含水率高于20%时,阻力值又有所增加。Mattech 等[18]研究发现干木材和新鲜材的钻针阻力的变化趋势和阻力幅值基本相同。德国Rinntech 公司创始人Rinn 等[1]研究发现:钻针阻力主要由木材密度决定,但木材含水率、新鲜木的预应力对钻针阻力的影响尚不明确。因此,含水率与钻针阻力之间的关系尚无一个统一的结论,仍有必要进一步研究木材含水率与钻针阻力之间的关系。
目前尚不清楚含水率与钻针阻力之间的具体关系,如果使用线性回归模型、多项式回归模型等传统模型来拟合含水率与钻针阻力之间的关系,拟合效果可能比较差,不能全面、清晰地反映出木材含水率与钻针阻力之间的关系。广义相加模型(generalized additional model,GAM)是对传统广义线性模型的非参数拓展,能综合处理线性关系和非线性关系的一种复合模型,可识别哪些自变量与因变量是线性关系,哪些自变量与因变量是非线性关系,以及各自变量对因变量的贡献率,并能建立基于线性自变量和非线性自变量的综合模型[19-20]。因此,本研究采用广义相加模型来研究含水率与钻针阻力之间的关系。
本研究使用德国Rinntech 公司生产的Resistograph 650-S 微钻阻力仪测量了包含软阔叶树、硬阔叶树和针叶树的9 个树种木材在不同含水率下的钻针阻力,建立各树种钻针阻力与木材含水率、木材绝干密度双因子之间的广义相加模型和钻针阻力与木材绝干密度单因子之间的广义相加模型,对比分析两个模型的拟合效果,研究木材含水率对钻针阻力的影响程度,并建立每个树种木材含水率与湿木状态下与绝干状态下钻针阻力差值之间的广义相加模型,分析每个树种木材含水率对钻针阻力的影响规律。
1 材料与方法
1.1 试验材料
试验材料是2020年9月—2021年3月在信阳师范学院校内的天然次生林中采伐的风倒活木以及近3 个月内新死亡的枯立木。在树高1.3、2.3和3.3 m 处选取树干通直、无明显缺陷处截取长度为0.4 m 长的树干,再把树干加工成3.0 cm×3.0 cm×3.0 cm 的正方体木块。试验材料基本情况如表1所示。
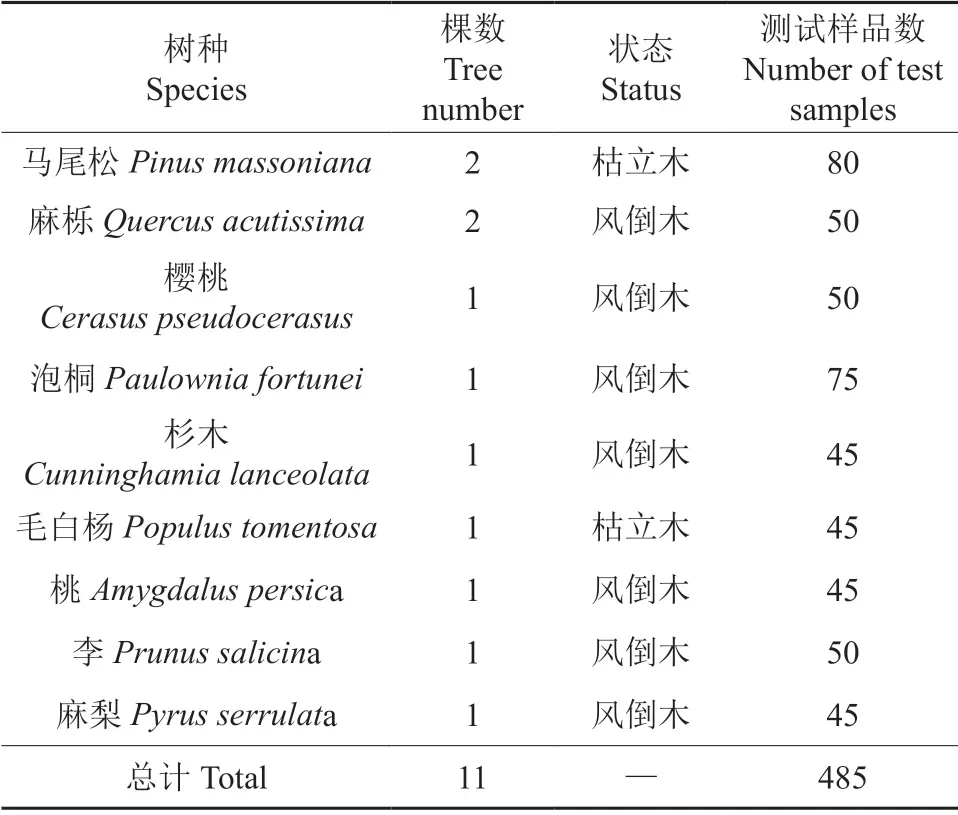
表1 试验材料基本情况Table 1 Basic information of test materials
1.2 试验仪器
试验仪器主要是德国Rinntech 公司最新推出的Resistograph 650-S 微钻阻力仪,该仪器钻针进给速度和旋转速度固定,钻针进给为60 cm·min-1,钻针旋转速度未知,钻针阻力采样间距为0.01 mm。阻力单位为该公司自定义的阻力单位“Resi”。该仪器配套有DECOM 钻针阻力处理软件,使用该软件打开阻力曲线图时,纵坐标表示钻针阻力的相对大小,且以百分比形式表示。
1.3 试验方法
1.3.1 湿木块钻针阻力取样方法
每个试验样品在湿木状态下取样一次钻针阻力。为了使试验样品含水率有较大的差异,同时防止木块干裂,本试验采用自然风干法调节木块的含水率,并分3 批次测量湿木钻针阻力,每批次取样时间间隔20 d 左右,具体方法如下:当试验样品加工好后,先取每个树种试验样品总数的1/3,使用Resistograph 650-S 微钻阻力仪沿木材径向方向钻入正方体木块,钻针钻入方向与木块的一条边平行,使用游标卡尺测量钻针路径长度,测量精度为0.01 mm,使用电子天平测量每个木块的质量m,精确到0.01 g;把剩下的木块均匀放置在储物架上,储物架通风良好,每间隔20 d 左右,取每个树种的总样品数的1/3,使用同样的方法测量每个木块的钻针阻力钻针路径长度和质量,直至所有树种湿木块测量完为止。
1.3.2 试验样品绝干密度测量方法
把在湿木状态下已经测量了钻针阻力的试验样品均匀放入烘箱中,把烘箱温度设置为45℃,恒温干燥6 h;再把烘箱温度设置为75℃,恒温干燥6 h;最后把烘箱温度设置为105℃,恒温干燥48 h,使木块干燥至绝干状态;关闭烘箱,试验样品温度降到室温状态时把试验样品放入玻璃干燥器中保存[14]。使用电子天平测量每个样品的绝干质量m0,测量精度为0.01 g。使用游标卡尺测量每个样品的长a、宽b、高h,精度为0.001 cm,最后利用体积法计算每个样品的绝干密度ρ(g·cm-3),计算公式为:

每个木块含水率MC 的计算公式为:

1.3.3 绝干木块钻针阻力取样方法
为了减小绝干状态下和湿木状态下所测量的钻针路径上木材密度的差异,绝干状态下钻针钻入方向与湿木状态下钻针阻力取样方向相同,两条测量路径之间的距离不宜过大。同时,为了防止两条测量路径交叉或者重合,两个钻针钻入点相距1 cm 左右。使用相同方法测量绝干木块的钻针路径长度。
1.4 数据处理
把每个木块的湿木状态下的钻针平均阻力、湿木状态下的含水率、绝干状态下的钻针阻力和绝干密度作为1 组数据进行处理。在钻麻梨时,有1个木块把钻针卡死,该组数据作异常数据处理,因此,共测得484 组有效数据。首先计算每个木块湿木状态下和绝干状态下的平均阻力,分析每个树种湿木含水率的平均值、标准差和变动系数以及湿木状态下与绝干状态下钻针阻力差值的平均值、标准差和变动系数,初步判断木材含水率与钻针阻力之间的关系。然后建立各树种木材含水率、木材绝干密度与钻针阻力之间的广义相加模型以及木材绝干密度与钻针阻力之间的广义相加模型,分析两个模型的拟合结果,以说明木材含水率对微钻阻力的影响程度。最后建立每个树种木材含水率与含水状态与绝干状态下钻针阻力差值之间的广义相加模型,分析每个树种木材含水率对钻针阻力的影响规律。
1.4.1 钻针阻力平均值计算方法
在钻针在钻入树木之前,钻针在钻针套头内空载移动8 mm 后才钻入木材;当钻针钻穿木块后,操作人员一般会延时10 s 左右才停止树木微钻阻力仪。因此,钻针在钻入木块前和钻出木块后各有一小段时间处于空载状态。图1是Resistograph 650-S 树木微钻阻力仪钻针阻力的变化过程,阻力曲线图的开始部分和结束部分钻针针头都处于空载状态,只有中间部分钻针针头处于负载状态。

图1 Resistograph 650-S 钻针阻力曲线图Fig.1 Drill resistance curve of Resistograph 650-S
钻针每前进0.01 mm,Resistograph 650-S 采样1 次钻针阻力,因此,根据钻针钻入木块前的空载位移和每个样品的钻针路径长度,选取每个测量数据中钻针在木块内的阻力数据的范围和阻力数据的个数,然后计算钻针钻在每个木块内部的平均阻力。具体方法如下:1)将Resistograph 650-S微钻阻力仪的.dpa 原始阻力记录文件转换成Excel格式;2)根据钻针钻入木块前的空载位移,计算钻针钻入木块的起始位置;3)根据钻针路径长度,计算钻针钻出木块的位置和钻针在木块内部阻力采样点的个数;4)分别计算每个木块在湿木状态下平均阻力R0和绝干状态下的平均阻力R1。
1.4.2 数据统计分析方法
为了分析含水率对钻针阻力的影响,本研究假设同一个试验样品在湿木状态下和绝干状态下钻针路径上的木材密度分布情况相同,即湿木状态下和绝干状态下木材密度对钻针阻力的影响是相同的,湿木状态下和绝干状态下钻针阻力的差异主要木材含水率的差异所引起的。绝干木材的含水率为0,因此,湿木含水率与湿木状态与绝干状态钻针阻力差值之间的关系可等价于含水率与钻针阻力之间的关系。为了初步分析含水率与钻针阻力之间的关系,统计分析每个树种湿木含水率的平均值、标准差和变动系数以及湿木状态下与绝干状态下钻针阻力平均值的差值的平均值、标准差和变动系数。每个测试样品湿木状态与绝干状态下钻针阻力平均值的差值dR计算公式为:

式(3)中,R0为湿木状态下钻针阻力平均值,R1为绝干状态下的钻针阻力平均值。
由于有些树种的dR是正数,有些树种的dR是负数,因此,在本研究中,变动系数d使用平均值μ的绝对值除以标准差σ计算,计算公式为:

1.4.3 广义相加模型GAM
广义相加模型是对传统广义线性模型的非参数拓展,能综合处理线性关系和非线性关系的一种复合模型。另外,广义相加模型可把自变量划分成多个连续的区间,每一个区间都能用独立的线性函数或者非线性函数来拟合,可有效处理自变量与因变量之间的关系随着自变量范围的变化而变化的复杂关系[20]。GAM 模型的形式为:

式(5)中,y为因变量,g为连接函数,β0为截距,x1,…,xn为自变量,f1,…,fn为连接自变量的平滑函数。模型拟合结果通过自变量的自由度、P、F统计值、调整后决定系数(R2)和方差解释率等参数来表示。当自变量的自由度为1 时,表示该自变量与因变量呈线性关系;当自变量的自由度大于1 时,表示该自变量与因变量呈非线性关系,且自由度的值越大,非线性关系越显著。P值表示统计结果的显著性水平,F统计值表示自变量的相对重要性,R2用来表示回归模型的拟合效果,方差解释率表示自变量对因变量总体变化的解释能力。
1.4.4 含水率对钻针阻力影响程度研究方法
如果含水率对钻针阻力没有显著影响,则湿木状态下的钻针阻力与绝干状态下的钻针阻力没有显著差异,钻针阻力主要受木材绝干密度这个单因子的影响。相反,如果含水率对钻针阻力有显著影响,则湿木状态下的钻针阻力与绝干状态下的钻针阻力有显著差异,钻针阻力不仅与木材绝干密度有关,而且与木材含水率有关。本研究以包括湿木状态和绝干状态下的钻针阻力为因变量,分别以木材含水率和木材绝干密度双因子为自变量、以木材绝干密度单因子为自变量,用薄板样条函数对各自变量进行平滑处理,薄板样条函数节点的最大个数设置为默认值,使用R 语言中的mgcv 包中的gam 函数建立各树种钻针阻力与木材含水率和木材绝干密度双因子之间以及与木材绝干密度单因子之间的广义相加模型,分析两模型拟合结果,主要分析R2、方差解释率和AIC这3 个拟合指标。如果两个模型的拟合结果无显著差异,说明含水率对钻针阻力无显著影响,如果两个模型的拟合结果存在显著差异,说明含水率对钻针阻力有显著影响。
1.4.5 含水率与钻针阻力之间的具体关系研究方法
以湿木含水率为自变量,以该木块在湿木状态下和在绝干状态下钻针阻力差值为因变量,用薄板样条函数对含水率进行平滑处理,薄板样条函数节点的最大个数设置为默认值,使用R 语言中的mgcv 包中的gam 函数建立每个树种含水率与钻针阻力差值之间的广义相加模型,分析各树种广义相加模型的拟合结果,绘制各树种阻力差值与木材含水率之间的拟合曲线,分析各树种木材含水率与钻针阻力之间的具体关系。
2 结果与分析
2.1 湿木含水率和钻针阻力差值的变动程度
各木块的湿木状态下的含水率以及湿木状态与绝干状态下钻针阻力差值的平均值、标准差和变动系数如表2所示。
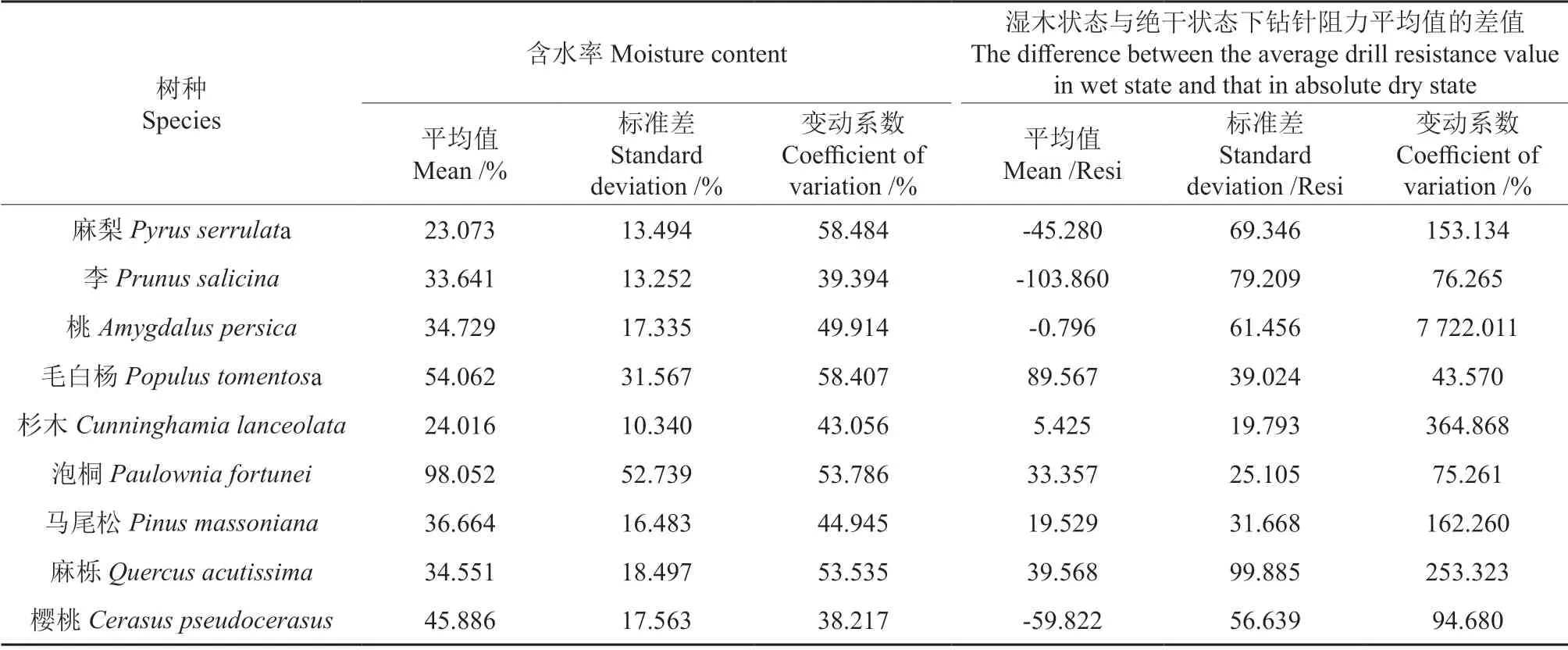
表2 木材含水率和钻针阻力差值平均值统计表Table 2 Statistical table of wood moisture content and the difference between the average drill resistance value in the wet state and the absolute dry state
从表2中可以看出:1)各树种木材平均含水率在23.073%~98.052% 之间,各树种平均含水率差异较大,各树种含水率的变动系数在38.217%~87.885% 之间;2)麻梨、李、桃和樱桃这4 个树种湿木状态与绝干状态下钻针阻力平均值差值的平均值小于0,说明这4 个树种湿木状态下的钻针阻力小于绝干状态下的钻针阻力,钻针阻力与木材含水率负相关,其他5 个树种的平均值大于0,说明这5 个树种湿木状态下的钻针阻力大于绝干状态下的钻针阻力,钻针阻力与木材含水率正相关;3)湿木状态与绝干状态下钻针阻力平均值的差值的变动系数在43.570%~7 722.011%,除毛白杨外,其他树种湿木状态与绝干状态下钻针阻力平均值的差值的变动系数均高于木材含水率的变动系数,且桃、杉木、麻栎这3个树种的阻力差值的变动系数过大,是木材含水率变动系数的5 倍以上,说明不同树种木材含水率对钻针阻力的影响程度不同。
2.2 含水率对钻针阻力的影响程度
各树种钻针阻力与木材含水率、木材绝干密度双因子之间的广义相加模型和与木材绝干密度单因子之间的广义相加模型的拟合结果如表3所示。
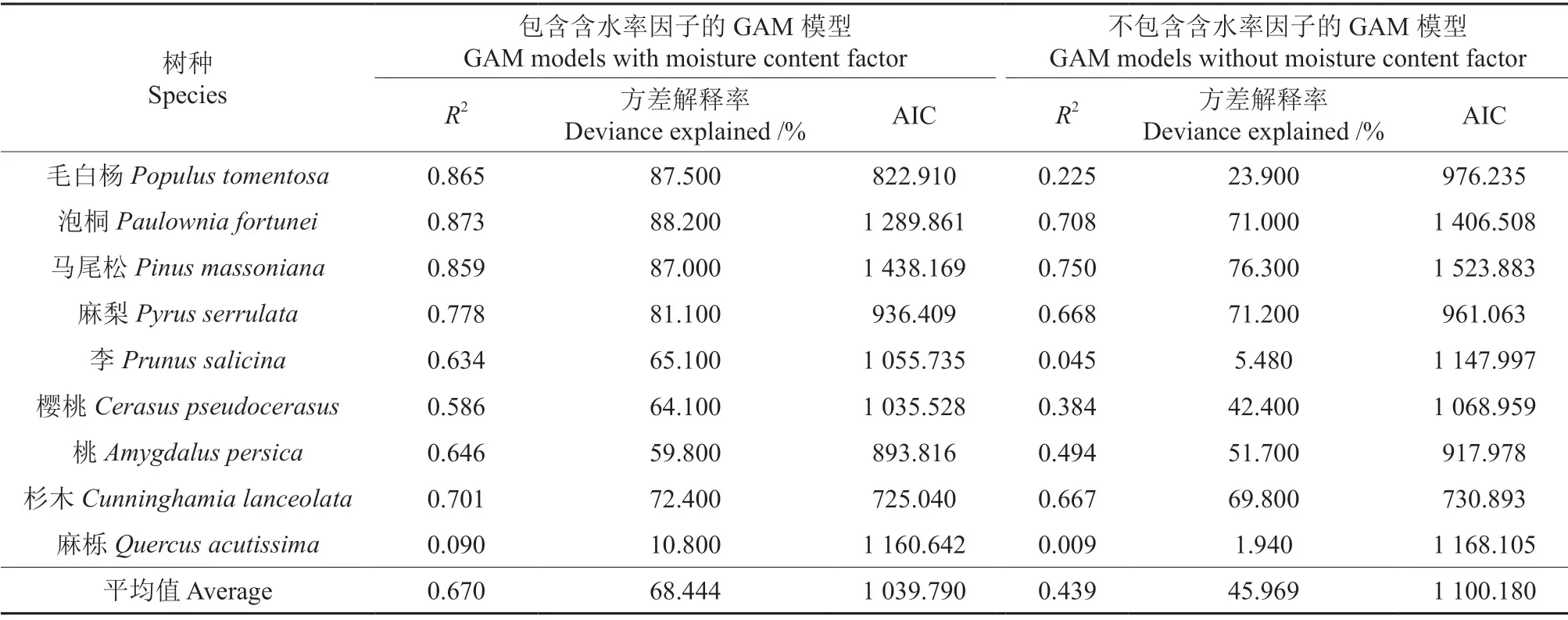
表3 包含含水率因子与不包含含水率因子的GAM 模型拟合结果Table 3 Fitting results of the GAM models with or without the moisture content factor
从表3中可以看出:1)每个树种不包含木材含水率的单因子模型的R2和方差解释率均小于包含木材含水率的双因子模型的R2和方差解释率,不包含木材含水率的单因子模型的AIC 均小于包含木材含水率的双因子模型的AIC;2)各树种包含木材含水率双因子模型R2的平均值比不包含木材含水率单因子模型R2的平均值高0.231,比不使用含水率因子的模型提高了52.620 个百分点;3)各树种包含木材含水率的双因子模型的方差解释率的平均值比不包含木材含水率的单因子模型方差解释率的平均值高22.475%,比不使用含水率因子的模型提高了48.892 个百分点;4)各树种包含木材含水率的双因子模型的AIC 的平均值比不包含木材含水率的单因子模型的AIC 的平均值低60.39,比不使用含水率因子的模型降低了5.489 个百分点。为了检验每个树种包含含水率与不包含含水率因子的GAM 模型是否存在显著差异,我们对每个树种的两个模型拟合结果使用anova 函数做F 检验,检验结果如表4所示。从表4中可以看出:每个树种的包含含水率因子与不包含含水率因子的GAM 模型在显著性水平0.01 上存在显著性差异。

表4 F 检验结果Table 4 Results of F-test
2.3 含水率对钻针阻力的影响规律
含水率与湿木与绝干木之间钻针阻力差值的相关关系如图2所示,图中实线为GAM 模型拟合值,点线之间的区域是置信度为95%的范围。含水率与阻力差值之间GAM 模型拟合结果如表5所示。
从图2中可以看出各树种的含水率与阻力差值之间GAM 模型拟合曲线形状差异较大。当木材含水率较低时,大部分树种湿木与干木之间的阻力差值随着木材含水率的增加而增大,当木材含水率增加到一定程度时,湿木与干木之间的阻力差值随着木材含水率的增加而减小。但有少量树种湿木与干木之间的阻力差值随着木材含水率的增加而减小。大部分树种的含水率与阻力差值的散点图大部分位于95%的置信范围内,少量树种的散点图位于95%的置信范围之外。从表5中可以看出各树种含水率与阻力差值的GAM 模型拟合结果差异较大。各树种GAM 模型的自由度在1~6.062 之间、P值在0~0.619 之间、F值在0.25~23.45、R2在0~0.644 之间、方差解释率在0.579%~66.7%之间,拟合结果差异很大,说明含水率对钻针阻力影响的规律和程度与树种有很大的关系,不同的树种含水率对钻针阻力影响规律和影响程度有很大的差异。
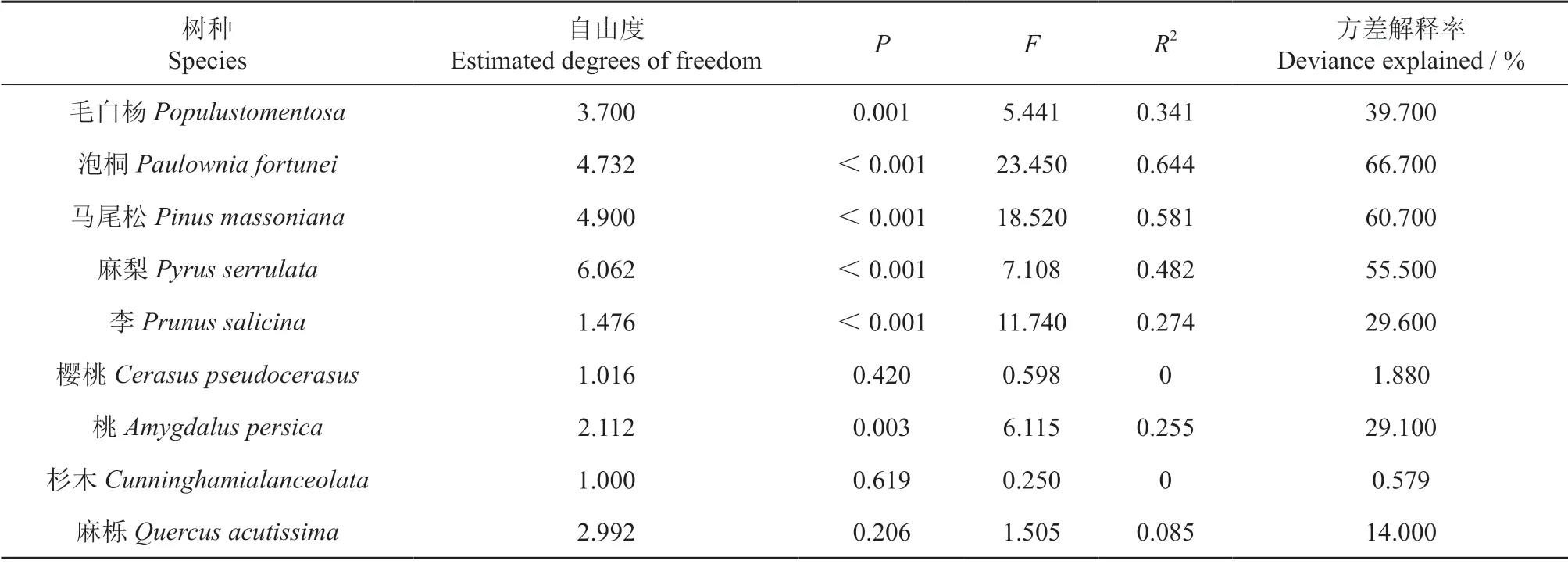
表5 含水率与阻力差值的GAM 模型拟合结果Table 5 GAM fitting results between moisture content and resistance difference

图2 含水率与阻力差值之间的相关关系Fig.2 Relations between moisture content and resistance difference
2.4 结果分析
在本研究中,各树种湿木状态下与绝干状态下钻针阻力差值与木材含水率之间的变化规律也存在很大差异。造成含水率与钻针阻力之间的关系差异较大的原因可能有:
1)钻针阻力与木材硬度、木材强度和木材韧性有关。破坏木材纤维所需要的能量与木材硬度、木材强度和木材韧性有关。木材硬度越大,钻针越难钻入木材,钻针在进给方向上的阻力越大,钻针与木材切削面的摩擦力越大,从而又导致钻针在旋转方向上的阻力越大。木材强度越大,破坏木材纤维所需要的能量越大,钻针在旋转方向上的阻力越大。木材韧性越大,木材所能抵御的瞬时最大冲击能量越大,木材被扩展出一个裂隙和破坏木材组织所需要的能量越高[14],钻针在旋转方向上的阻力越大。当木材含水率在纤维饱和点以上时,木材含水率对木材的力学性质几乎没有影响,含水率对钻针阻力的影响较小。当木材含水率在纤维饱和点以下时,木材含水率与木材硬度和木材强度负相关,木材韧性正相关。当木材含水率发生变化时,如果木材硬度和强度变化所引起的钻针阻力的变化幅度大于木材韧性变化所引起的钻针阻力变化幅度时,钻针阻力与木材含水率负相关;如果木材硬度和强度变化所引起的钻针阻力的变化幅度小于木材韧性变化所引起的钻针阻力变化幅度时,钻针阻力与木材含水率正相关;如果木材硬度和强度变化所引起的钻针阻力的变化幅度与木材韧性变化所引起的钻针阻力变化幅度的差异不显著时,含水率对钻针阻力的影响也将不显著。由于各树种木材纤维饱和含水率存在较大差异,且木材的硬度、强度和韧性随木材含水率的变化规律也存在较大差异,因此,各树种钻针阻力与木材含水率的变化规律存在较大差异。
2)钻针阻力受木材纤维之间连接的紧密程度的影响。钻针阻力与木材纤维之间的连接力正相关。由于各树种木材的干缩率和湿胀率存在较大差异,当木材含水率发生变化时,木材纤维之间的连接力的变化规律不同。如果木材的干缩率和湿胀率较小,当木材含水率增加时,木材纤维膨胀,木材纤维之间的间隙变小,木材纤维之间的连接力增加,使钻针阻力呈上升趋势变化;当木材含水率减小时,木材纤维收缩,木材纤维之间的间隙变大,木材纤维之间连接力减小,使钻针阻力呈下降趋势变化。如果木材的干缩率和湿涨率较大,当木材含水率减小时,尽管木材纤维要收缩,但木材体积也要减小,使木材变得更加致密坚硬,木材纤维之间连接力增加,使钻针阻力呈上升趋势变化;当木材含水率增加时,木材体积增大,尽管木材纤维要膨胀,但木材体积也要增加,木材变得相对稀疏柔软,木材纤维之间连接力减小,使钻针阻力呈下降趋势变化。因此,当木材的干缩率和湿胀率较小时,钻针阻力与木材含水率正相关;当木材的干缩率和湿胀率较大时,钻针阻力与木材含水率负相关。
3)钻针阻力与树脂含量及状态有关。树脂对木材力学性质有较大影响[14]。树脂含量越高,木材纤维之间连接力越大,钻针阻力越大。同时,钻针阻力受树脂状态的影响较大。当树脂处于液态时,树脂对钻针阻力影响较小,当树脂处于固态时,树脂对钻针阻力影响较大。在活立木和新鲜材中,树脂处于液态,对钻针阻力的影响较小;在干材中,树脂处于固态,对钻针阻力影响较大。木材含水率越低,含有树脂较高的木材越坚硬,钻针阻力越大。因此,当树脂含量较高时,钻针阻力与含水率负相关。
4)钻针阻力受钻针路径、钻针磨损程度、钻针振动幅度等因素的影响。钻针阻力只能反映出钻针路径上的木材力学性质特征,而木材是典型的非均质材料,不同路径上的钻针阻力存在较大差异。在测量同一试件不同含水率的钻针阻力时,钻针路径是不相同的,因此不同的钻针路径也会导致钻针阻力存在一定的差异。随着钻针使用次数的增加,钻针针头磨损越厉害,钻针锋利程度下降,钻针阻力增大。所以,不同的测试次序也会导致钻针阻力值存在差异。微钻阻力仪钻针长500 mm,针杆直径1.5 mm,钻针又细又长,当钻针高速旋转时,钻针振动幅度较大,特别当木材材质比较坚硬时,钻针振动幅度很大,导致钻针阻力变化幅度很大。因此,每次取样钻针阻力时,钻针震动幅度可能存在一定的差异,导致钻针阻力存在一定的差异。所以,微钻阻力仪测量的钻针阻力存在一定的测量误差,当木材含水率对钻针阻力影响的幅度小于阻力测量误差时,钻针阻力不能反映出含水率对钻针阻力的影响。
在本研究中,毛白杨、泡桐、马尾松、麻梨这4 个树种,当含水率低于某一个阈值时,湿木与绝干状态下的钻针阻力差值随含水率的增加而增加,当含水率高于某一个阈值时,湿木与绝干状态下的钻针阻力差值随含水率的增加而减小,直到阻力差值趋于一个稳定值,说明在这4 个树种中,当含水率从绝干状态逐步增加时,钻针阻力增加,当含水率增加到某个值时,钻针阻力值最大,当含水率再增加时,钻针阻力值逐渐减小直到一个稳定的值。这可能是这4 个树种的木材在处于绝干状态时,木材韧性较小,木材纤维之间的连接力较小,使钻针阻力值较小。当含水率从绝干状态逐步增加时,木材韧性增加对钻针阻力的影响程度大于木材强度和硬度变小对钻针阻力的影响程度,使钻针阻力增加。当含水率增加到某一个值时,木材韧性增加对钻针阻力的影响程度小于木材强度和硬度下降对钻针阻力的影响程度,使钻针阻力减小。当木材含水率增加到饱和状态时,钻针阻力受含水率的影响较小。麻梨、李、桃和樱桃这4 个树种湿木状态与绝干状态下钻针阻力平均值差值的平均值小于0,说明从整体上这4 个树种钻针阻力与木材含水率负相关,这可能是果木木材的树脂含量较高、木材干缩率和湿胀率较大引起的,木材含水率越低,木材越坚硬致密,钻针阻力较大。杉木、樱桃和麻栎的含水率与湿木状态与干木状态下钻针阻力差值的GAM 模型拟合结果非常差,这3 个树种的GAM模型的R2均为0。在本试验中,杉木的年轮线不规则,樱桃树的髓心附近的纤维较粗,钻针较大,导致这两个树种不同路径下的钻针阻力差异较大。麻栎木材密度大,钻针震动幅度较大,使钻针阻力变化幅度较大。因此,在本试验中,杉木、樱桃和麻栎3 个树种钻针阻力不能反映出含水率对钻针阻力的影响关系。
3 结论与讨论
3.1 结 论
1)含水率对钻针阻力有显著影响。各树种包含木材含水率和木材绝干密度双因子GAM 模型的拟合效果比仅包含木材绝干密度单因子GAM 模型的拟合效果在显著性水平0.01 上有显著性提高,R2平均提高了52.620 个百分点,方差解释率平均提高了48.892 个百分点,AIC 平均降低了5.489个百分点。
2)从宏观上分析,麻梨、李、桃和樱桃这4个树种钻针阻力与木材含水率负相关;毛白杨、泡桐、马尾松、杉木、麻栎这5 个树种钻针阻力与木材含水率正相关。
3)从微观上分析,含水率对钻针阻力影响规律差异较大,对杉木、樱桃和李树这3 个树种的影响呈线性或者近似线性规律变化;对毛白杨、泡桐、马尾松、桃、李、麻栎这6 个树种的影响呈非线性规律变化,且影响规律差异较大。
因此,在使用微钻阻力仪时,需要尽量减小被测对象之间含水率的差异,如果被测对象含水率差异较大时,需要建立不同树种含水率与钻针阻力之间的数据模型,以提高微钻阻力仪的测量精度。
3.2 讨 论
微钻阻力仪钻针阻力受木材力学强度的影响,由于木材的力学强度受木材含水率的影响比较大,为了科学、合理地解释微钻阻力仪钻针阻力,本研究进一步研究含水率对钻针阻力的影响程度,减小含水率对微钻阻力仪测量精度的影响。尽管已经有大量学者研究了含水率与钻针阻力之间的关系,但研究结果存在较大差异。Ukrainetz 等[22]测试了含水率分别为19%、25%和168%的云杉树干的阻力,研究发现含水率对钻针阻力有较大影响,钻针阻力随着木材含水率的增加而增大。张晓芳等[23]把新鲜落叶松、新鲜毛白杨、新鲜杉木、旧落叶松、旧楠木和旧红松加工成2 cm×2 cm×2 cm 试件,新鲜木材的含水率分别控制在0%(绝干状态)、12%左右(气干状态)、30%左右(平衡含水率)和100%,旧木材的含水率控制在12%左右,在不同含水率下使用微钻阻力仪取样每个试件的阻力数据,研究发现:含水率对新鲜落叶松和新鲜杉木阻力影响不太显著,且未发现含水率对这2 个树种的钻针阻力影响规律;含水率对新鲜毛白杨阻力影响非常显著,且钻针阻力随着含水率的增加而增加。王燕婷[24]把杉木(Chinese fir)木材加工成80 个2 cm×2 cm×30 cm 的试件,使用恒温恒湿箱和干燥箱将试件含水率分别控制在0%、6%、9%、12%、15%、18%、24%和30%,在不同含水率下使用微钻阻力仪对每个试件取样3 次阻力数据,研究发现:微钻阻力仪旋转方向和进给方向上的阻力均与含水率负相关,旋转方向上钻针阻力与含水率的线性方程为R=728.252-9.439MC (R2=0.988,F=503),进给方向上的钻针阻力与含水率的线性方程为R=593.787-6.63MC (R2=0.994,F=1 070.59)。从本研究中,麻梨、李、桃和樱桃这4 个树种钻针阻力与木材含水率负相关;毛白杨、泡桐、马尾松、杉木、麻栎这5 个树种钻针阻力与木材含水率正相关。本研究分析了包含软阔叶树、针叶树、硬阔叶树的9 个树种钻针阻力与木材含水率之间的关系,研究结果对研究含水率与钻针阻力之间的关系有一定的推动作用,但仍不能确定木材含水率对钻针阻力影响的机理,在以后仍需进一步研究。
致谢:感谢中国林业科学研究院唐守正院士对论文的选题及撰写等给予的精心指导。

