基于连清数据的广东杉木人工林生物量模型构建
郭泽鑫,曹 聪,刘 萍
(华南农业大学 林学与风景园林学院,广东 广州 510642)
森林生物量是指森林植物群落在其生命过程中产生的干物质积累量,以乔木层生物量为主,包括地上生物量(Above-ground biomass,AGB)和地下生物量(Below-ground biomass,BGB)。森林生物量是碳封存的主要载体,约占陆地碳库的45%、全球碳库的31%[1],在维系陆上碳循环和稳定全球气候方面发挥着主导作用,其中AGB已被确认为全球气候观测系统(Global Climate Observing System,GCOS)54 个基本气候变量之一。因此,有关森林生物量计算方法和估算精度一直是林学和生态学研究的重点和热点。杉木Cunninghamia lanceolata具有易繁殖、生长快、产量高和材质优等特点,是我国南方主要造林树种之一,也是我国亚热带地区特有的速生针叶用材树种,广东杉木林面积占乔木林面积的10.32%,在主要树种中位居第二。
国内对杉木生物量研究较早[2],曾伟生等[3]以贵州杉木人工林为对象,构建了与材积相容的杉木地上生物量模型,随后又将全国划分为两个总体研建了杉木通用性生物量模型[4],蔡兆炜等[5]以福建杉木为对象,基于胸径、树高构建了杉木地上部分总量和分量相容的生物量模型,曾伟等[6]以江西杉木人工林为对象,构建了基于林龄、胸径和林分密度的杉木生物量模型,此外,国家林业局[7]也颁布了杉木生物量模型的相关行业标准。上述模型都是基于单木水平的,不便于估测林分尺度或者区域尺度杉木生物量。杉木林分水平生物量模型研究较少,方精云等[8]构建了杉木生物量与蓄积量之间的换算模型,但存在样本量少、未分区域建模等问题。赵嘉诚等[9]独立拟合了杉木地下生物量和根茎比的林分模型,但主要研究地下生物量,没有考虑到地上、地下生物量之间的相容性。曾伟生[10]采用分段建模方法构建了杉木材积源生物量模型,但仅构建了总量模型,无法分析地上和地下生物量分布状况,且样本取自全国,未考虑立地、林分起源、林龄、树种组成等对生物量的影响。鉴于此,本研究以广东省杉木人工林为研究对象,基于2007、2012、2017年3 期广东省森林资源连续清查数据,采用非线性度量误差联立方程组联系地上、地下生物量,考虑不同林分发育阶段,引入龄组哑变量参与建模,构建了基于林分因子以及材积源两种杉木人工林生物量预测模型,精准估测广东杉木人工林生物量碳储量,对提高广东杉木人工林森林经营成效与森林碳汇效益评价具有重要指导意义。
1 材料与方法
1.1 材料来源
数据采用2007、2012、2017年广东省森林资源连续清查225 块杉木人工林固定样地及样木数据,样地活立木株数不少于25 株,以杉木人工林纯林为主,少量杉木蓄积占比不低于65%的相对纯林,以混交比例为因素进行方差分析检验,结果显示不同杉木蓄积占比的样地林分生物量差异不显著。按照《森林资源连续清查技术规程》(GB/T 38590-2020)进行龄组划分,幼龄林、中龄林、近熟林、成熟林和过熟林样地数量占比分别为37%、42%、9%、11%和1%。随机抽取180块样地建模,另外45 块样地检验,建模样地和检验样地各龄组比例均为37%、42%、9%、11%和1%。建模样地主要林分因子特征见表1。

表1 建模样地林分因子特征Table 1 Characteristics of stand factors for modeling
样地生物量由各样地内的单木生物量汇总得到。单木生物量的计算采用已发布的相关单木生物量模型,杉木及少量伴生树种马尾松Pinus massoniana、湿地松Pinus elliottii、木荷Schimasuperba、枫香Liquidambar formosana、栎类Quercus和柳杉Cryptomeria fortunei以原国家林业局颁布的行业标准中的一元模型进行地上及地下生物量估算[7,11-16],样地内水杉数量很少,直接用杉木模型替代计算,没有相关行业标准的树种(组),采用曾伟生等[17-18]提出的通用性地上生物量模型计算,地下生物量分针叶树和阔叶树利用根茎比换算得到:


式(1)~(3)中:Ma为地上生物量,Mb1为针叶树地下生物量,Mb2为阔叶树地下生物量,D0为单木胸径,a为参数,符合关系式a≈0.3p,p为木材基本密度。建模样地各龄组生物量特征见表2。
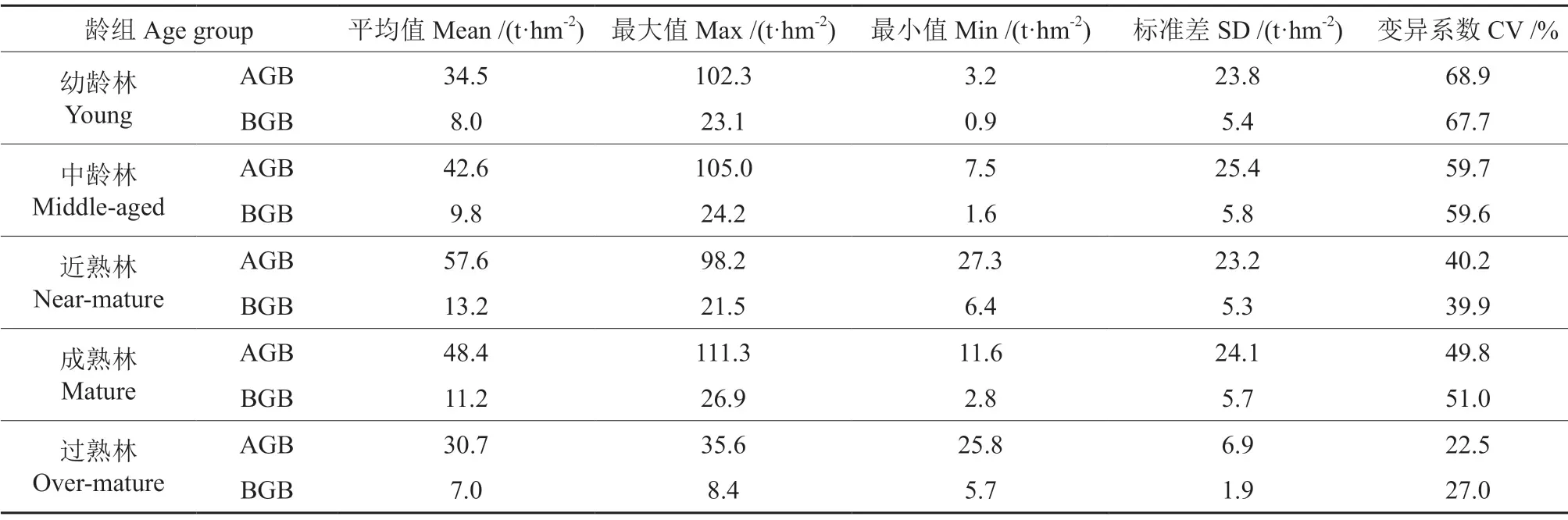
表2 建模样地各龄组生物量特征Table 2 Biomass characteristics of all age groups for modeling
1.2 研究方法
1.2.1 模型设计
建模类型采用两种常用的生物量模型,一种是基于林分因子的生物量模型,即直接构建生物量与林分特征因子之间的回归关系;另一种是材积源生物量模型,即构建生物量与蓄积量之间的转换模型,其实质是构建生物量转扩因子(Biomass conversion and expansion factor,BCEF)[19-20]与林分特征因子之间的回归关系。同时,为了研究林分发育阶段对生物量的影响,每种模型内部又分为常规模型和含龄组因子的哑变量模型,设置变量z=(z1,z2,z3)为反映不同龄组的哑变量[21],z=(1,0,0)代指幼龄林,z=(0,1,0)代指中龄林,z=(0,0,1)代指近熟林,z=(0,0,0)代指成、过熟林。共构建8 套模型系统,分别编号为模型系统Ⅰ~Ⅷ。
建模形式采用含加性误差的非线性模型作为构建模型的基本结构[22-23],以易于得到且与生物量相关性较高的林分胸高断面积(G)、林分平均胸径(D)和林分平均树高(H)等林分因子作为解释变量进行建模。参数估计方法上,为了实现同一套数据所构建的地上、地下生物量模型具有相关性和整体性,本研究构建相容性生物量模型,将地上生物量(AGB)和地下生物量(BGB)视为含度量误差的变量,其他变量视为无误差变量,采用非线性度量误差联立方程组的方法对地上和地下生物量进行联合估计[21],实质上就是以根茎比(Root-shoot ratio,RSR)作为中介,将地上和地下生物量关联起来。
杉木林分生物量模型的具体形式见表3。各式中,G为林分胸高断面积(m2·hm-2),D为林分平均胸径(cm),H为林分平均树高(m),V为单位面积蓄积量(m3·hm-2),AGB 为地上生物量(t·hm-2),BGB 为地下生物量(t·hm-2),RSR为根茎比(无量纲),BCEF 为生物量转扩因子(t·m-3)。εa、εb、εr、εbc为各独立方程的误差项。a0、a1、a2、b0、b1、b2为方程通用参数,a0i、a1i、a2i、b0i、b1i、b2i为哑变量z的特定参数(i=1,2,3)。

表3 杉木林分生物量模型的结构形式Table 3 Structural forms of the biomass models of Cunninghamia lanceolata stands
1.2.2 异方差处理
对于模型中存在的异方差问题,本研究采用特定权函数法进行加权回归,对各个模型系统中的每个模型分别按一般非线性回归进行独立拟合,得到每个独立模型的残差平方(ei2),按下式拟合ei2与模型自变量之间的回归关系[24]:

式(4)中:中c0、ci为参数,xi为每个独立模型的自变量,对于模型系统Ⅰ和Ⅲ,xi取G,Ⅱ和Ⅳ取G、H;而对于模型系统Ⅴ和Ⅶ,xi取D,Ⅵ和Ⅷ取D、H。得到每个独立模型的权函数对每个模型两边同时乘以权重变量,然后再利用非线性度量误差联立方程组进行参数估计。
1.2.3 模型评价与检验
一般最小二乘法追求总误差最小,而加权回归估计追求的是总相对误差最小,因此残差平方和、剩余标准差等指标不适用于加权回归的模型评价[25]。故本研究拟用曾伟生[26]提出的6 项基本评价指标进行模型评价,分别为决定系数(R2)、估计值的标准差(SEE)、总相对误差(TRE)、平均系统误差(MSE)、平均预估误差(MPE)和平均百分标准误差(MPSE)。R2和SEE 可以反映回归模型拟合优度,TRE 和MSE 反映模型系统偏差,其值应控制在±3%或±5%以内,趋于0 时效果最好,MPE 和MPSE 反映模型预估精度,从实用性角度出发,MPE一般要求保持在3%以内,MPSE 要求保持在15%以内。
常规模型与哑变量模型之间进行差异性检验,以分析是否有必要引入哑变量,本研究采用F检验法:

式(5)中:SSEcon为常规模型的残差平方和,SSEdum为哑变量模型的残差平方和,dfcon为常规模型的自由度,dfdum为哑变量模型的自由度。
利用45 块检验样本分别代入已构建的模型Ⅰ~Ⅷ,得到检验样本的生物量预估值,拟合检验样本预估值与观测值之间的线性回归关系,即y=b+ax,并得到对应的系数、R2值。当a越接近1、b越接近0 且拥有较高的R2时,可以认为预估值与观测值不存在明显的偏差,表示模型的预估精度高。
1.2.4 数据处理
每个独立模型权函数的确定采用EViews 10.0软件的非线性回归进行计算,每个模型系统的回归估计采用ForStat 2.2 软件的含误差变量的非线性联立方程组模块进行计算。图片制作在Origin 2018 软件上完成。其他数据处理采用Excel 软件。
2 结果与分析
2.1 模型评价
生物量模型参数估计见表4,基于林分因子的生物量模型评价结果见表5,材积源生物量模型评价结果见表6。从表5~6 的评价指标来看,所有模型的R2均在0.94 以上,即各模型引入的变量均解释了生物量变动的94%以上。SEE 均在0.94~5.00 t·hm-2之间。TRE 在±1.35%范围内,MSE 在±2.97%范围内,两者都保持在±3%之间,说明所建模型都不存在明显的系统偏差。MPE 在1.07%~2.10%之间,符合低于3%的要求,在95%置信区间内所有模型对生物量的平均预估精度均达到97.90%以上。MPSE 在5.31%~10.83%之间,均保持在15%以内。可见本研究所构建模型均达到较好的拟合效果,具有较高的预估精度。
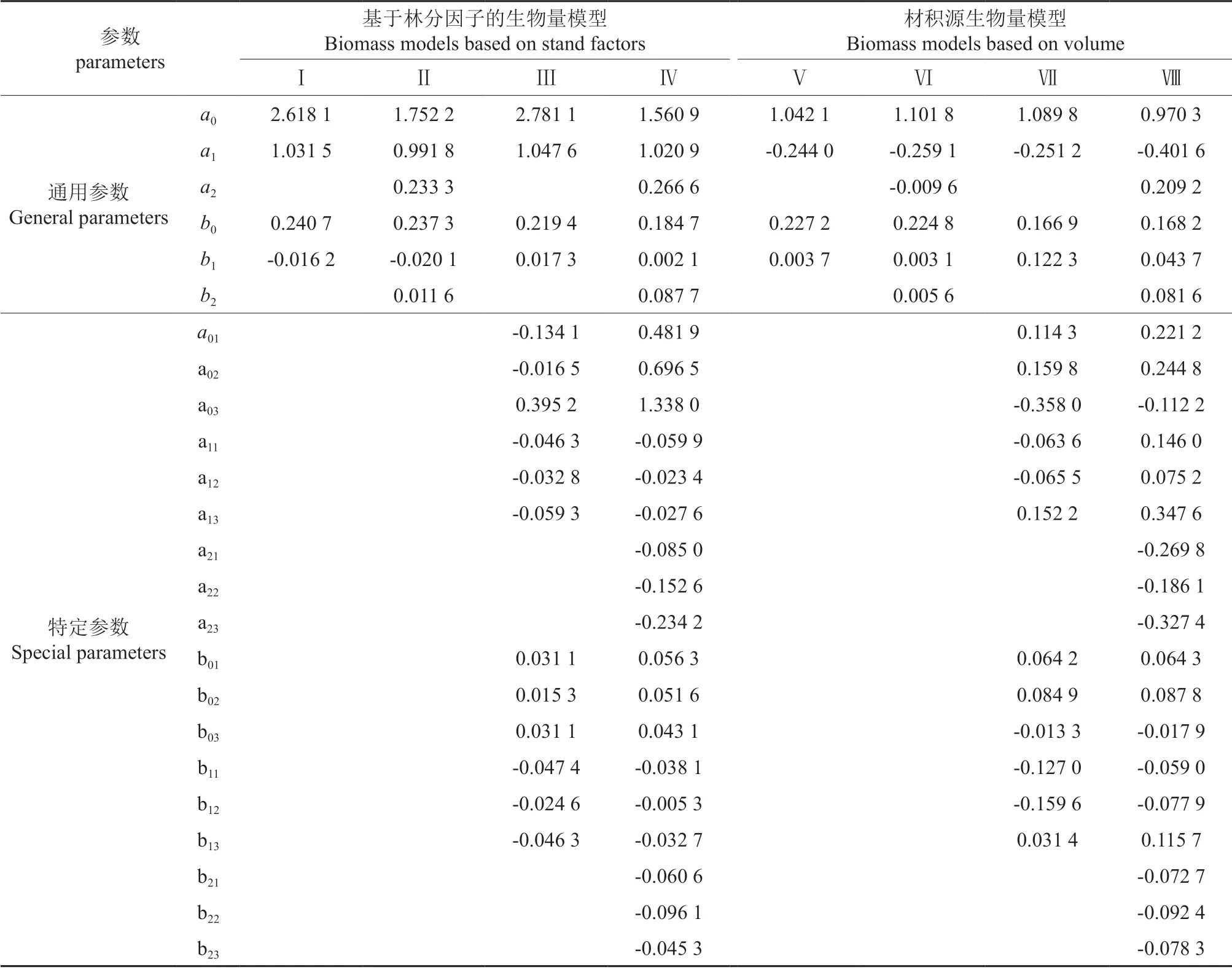
表4 生物量模型参数估计值Table 4 Parameter estimation of the biomass models

表5 基于林分因子的生物量模型评价统计指标Table 5 Statistical indices for the biomass models based on stand factors

表6 材积源生物量模型评价统计指标Table 6 Statistical indices for the biomass models based on volume
材积源生物量模型与对应的基于林分因子的生物量模型相比,有更高的R2以及更低的MPE和MPSE,说明材积源生物量模型的拟合优度更好,预估精度更高,总体拟合效果优于基于林分因子的生物量模型。对比各一元模型和对应的二元模型,可以发现引入林分平均树高后,各模型的拟合效果普遍得到提升,但差异并不显著,模型系统Ⅵ可能受权函数影响,拟合效果反而比模型系统Ⅴ略差。除了模型系统Ⅵ外,其他二元模型与对应一元模型相比,R2提升幅度在0.08%~1.50%之间,其他误差指标则没有呈现出明显的变化趋势,进一步说明引入林分平均树高对提高模型拟合效果和预估精度意义不大。
模型系统Ⅲ与Ⅰ之间AGB 的F统计量为18.35,BGB 则为12.61,均大于对应临界值2.15,模型系统Ⅳ与Ⅱ之间的AGB 和BGB 的F统计量分别为6.82 和4.87,两者均大于对应临界值1.94。对于材积源生物量模型,模型系统Ⅶ与Ⅴ之间、Ⅷ与Ⅵ之间的AGB 和BGB 的F统计量也均大于对应的临界值(2.15 和1.94)。说明哑变量模型与常规模型在0.05 水平上均存在显著性差异,引入龄组因子对模型有显著影响。
限于篇幅,本研究仅列出哑变量模型的相对残差图(图1),可见各模型的相对残差围绕0%上下均匀分布,没有明显随生物量预估值的变化而出现发散、收敛等现象,不存在明显的系统偏差,也不存在明显的异方差,材积源生物量模型的相对残差更接近于0%。

图1 哑变量模型相对残差图Fig.1 Relative error diagrams of the dummy variable models
2.2 模型检验
将45 个检验样本的数据分别代入到16 个模型中,得到预估值,建立预估值y与观测值x之间的线性回归关系,即y=b+ax。得到所有模型的R2均 在0.94 以 上,a均 在0.9~1.0 之 间,b在0.04~2.76 之间,多数在0~1 之间,整体上所有模型的散点都围绕预估线均匀分布,观测值与预估值没有明显的偏差,其中模型系统Ⅴ-Ⅷ的预估效果要好于模型系统Ⅰ-Ⅳ。模型系统Ⅶ预估效果最好,在较高的R2下,a最接近1,b最接近0。限于篇幅,图2仅展示哑变量模型的预估值和观测值的拟合图。

图2 哑变量模型的预估值和观测值的拟合图Fig.2 Fitting diagram of the predicted and observed values of the dummy variable models
2.3 模型优选
综合以上分析可知,本研究所建模型均具有较好的拟合效果,误差和精度符合相关要求,不存在明显的异方差现象,材积源生物量模型拟合效果优于对应的基于林分因子的生物量模型,含龄组因子的哑变量模型较常规模型具有显著提升,引入林分平均树高的二元模型较一元模型拟合效果有不同程度的提升。可见本研究中含龄组因子的材积源生物量模型更优,二元模型虽然拟合效果更好,但相较一元模型并没有显著提升。树高存在测量难度高、测量误差大等问题,其测量往往受限于地形、林分密度等多重因素,精度远不及胸径,且森林资源连续清查中林分平均树高为主林层优势树种平均木的算术平均高,标准木的选择受人为主观因素影响较大,测量结果存在较大的波动性和不确定性。基于上述分析,本研究认为引入林分平均树高意义不大,且会增加实践中的工作量,从精确性和实用性角度出发,推荐采用含龄组因子的一元材积源生物量模型,即模型系统Ⅶ,其回归方程见表7。

表7 模型系统Ⅶ的回归方程Table 7 Regression equations of model system Ⅶ
3 讨 论
实际上除了文中出现的模型外,本研究还尝试过直接以D、H、DH、D2H 等作为变量构建林分模型,但结果并不理想,R2基本都在0.3 以下,这主要是因为D、H都是均值,没有考虑到林分密度的影响。林分生物量模型不同于单木生物量模型,采用林分平均胸径、林分平均树高等只反映林木生长状况的因子进行建模往往得不到最优的拟合效果,特别是在样本的林分密度差别很大的情况下,因为生长状况很好的林分也可能由于密度低而导致生物量低,反之亦然。本研究仅用林分胸高断面积一个变量进行建模就达到了很好的拟合效果,说明林分胸高断面积是构建林分生物量模型的一个重要预测变量,与前人的研究基本相符[27-29]。这可能是因为林分胸高断面积不仅体现了林分的横向生长状况,同时反映了林分的密度状况,兼顾了林分的生长与总量特征。而对于材积源生物量模型,由于蓄积量这一变量的引入,使得模型本身就已经考虑到了林分的密度状况,所以在选择其他变量时可以不再考虑林分密度的影响。综上,在构建林分生物量模型时,需要引入能够体现林分密度的相关指标,如株数密度、林分密度指数等直接指标,也可以是林分胸高断面积、蓄积量等间接指标,在密度差别很大的林分中,密度指标对模型精度影响很大,本研究中G和V都在各自模型中起到主导作用,对模型拟合效果影响最大。
材积源生物量模型拟合效果要优于基于林分因子的生物量模型,这可能是由于前者包含了蓄积量这一因子。根据生物量的定义可以知道,对于树干而言,生物量实际上就是树干密度与树干材积的乘积,因此,树干生物量与树干材积具有高度相关性,而树干生物量又占据地上生物量的绝大部分,因此引入蓄积量后,地上生物量模型会得到更好的拟合效果,且相容性模型中地上与地下生物量模型可以相互转化,所以地下生物量模型的拟合效果也相应得到优化。董利虎等、曾伟生等以及Jagodziński 等研究也认为林分生物量与蓄积量有高度相关性[27,30-31]。在0.05 显著性水平上,本研究所建常规模型与对应的哑变量模型之间都存在显著差异,说明林分发育阶段对杉木林分生物量模型的拟合效果有显著影响,建模时有必要考虑林龄的影响。林龄对生物量影响主要体现在两个层面,一是自然层面,如林木的生长发育、衰老枯损,以及伴随林木生长所造成的林分自然稀疏等,都会对林分生物量造成影响;二是人为层面,人工林中不同发育阶段的林分会采取不同的抚育措施,为了促进郁闭、减少抚育成本,我国杉木的初植密度普遍较大,往往需要在幼中龄阶段采取一定的抚育间伐措施,从而改变林分密度以及对林木的胸径、树高、材积等生长指标产生影响,进而对林分生物量造成影响[32],洪奕丰等[33]在研究长白落叶松人工林林分生物量模型时也有相似结论。
本研究所建杉木生物量模型为林分尺度模型,目前相关研究还比较少,其中最具影响力的是方精云等[8]提出的基于蓄积量的杉木总生物量模型B=22.541 0+0.399 9V,曾伟生[10]也采用分段建模的方法构建了杉木的材积源生物量模型,其形式为B=0.100 4+0.786 7V(V<50 m3·hm-2)和B=6.979 9+0.649 1V(V≥50 m3·hm-2)。将本研究检验样本的数据代入到上述研究的模型中,构建预估值与观测值之间的线性回归关系y=b+ax,得出各模型的(a,b,R2),并计算总相对误差(TRE)。方精云模型的(a,b,R2)为(0.58,21.69,0.99),TRE 为3.47;曾伟生模型为(0.98,2.18,0.99),TRE 为-1.78;而本研究推荐模型(模型系统Ⅶ)为(0.98,0.27,0.99),TRE 为1.32。3 种 模型预估值与观测值线性拟合结果的R2都很高,也十分接近,但本研究模型的斜率a是最接近1 的,截距b也是最接近0 的,曾伟生模型次之,方精云模型偏差最大,且其b值很大,说明生物量水平较低时存在明显高估现象,从TRE 的绝对值来看,其结论也是一致的,本研究模型的总相对误差是最小的。与上述研究模型相比,本研究模型主要有以下几个优势:首先,虽然本研究建模样本数量没有曾伟生模型多,但本研究样本全部取自广东地区,样地伴生树种的组成更贴近广东杉木林的实际情况,且去除了占比很少的天然林,充分考虑到了地域、树种组成、起源等因素的影响;其次,本研究区分龄组建模,能反映不同林龄的杉木生物量情况;再者,本研究构建杉木地上和地下生物量的相容性模型,与总量模型相比,可以研究地上和地下生物量的分布情况。
模型系统Ⅶ对检验样本BCEF 的预估范围为0.45~0.68 t·m-3,均值为0.59 t·m-3;对RSR 的预估范围为0.22~0.24,均值为0.23。左舒翟等[34]基于全国各省份杉木林生物量的文献数据整理获得中国杉木林的BCEF 均值为0.616 t·m-3,RSR 的均值为0.247,两者均与本研究结果相近。但不同的是,本研究并没有将生物量估算参数视作常数,以均值来代表所有情况,而是以模型来估算不同林分特征杉木林的BCEF 和RSR,其结果更符合实际。
本研究设计和构建的生物量模型均具有较好的拟合效果,但仍存在一些不足有待进一步改进。虽然建模过程中考虑到了林分发育阶段的影响,但样本中以中幼龄林占绝大多数,成、过熟林占比很小,尤其是过熟林,这可能导致所建成、过熟林模型代表性不足,因为样本量不够大的情况下难以排除个案对总体估计的干扰,少量的样本可能无法反映总体的实际情况。
4 结 论
本研究基于2007、2012、2017年3 期广东省森林资源连续清查的数据,以广东省杉木人工纯林和相对纯林为研究对象,通过已建立的相应单木生物量模型计算并汇总得到每个固定样地的林分生物量,采用非线性度量误差联立方程组以及哑变量建模的方法,构建了基于林分因子的生物量模型以及材积源生物量模型,得到以下结论:
1)所构建的8 个模型系统共16 个地上、地下生物量模型都有较好的拟合效果,决定系数R2均大于0.94,不存明显的系统偏差,95%置信区间内平均预估精度都可达到97.90%以上。
2)构建林分生物量模型需兼顾林分的生长与密度,林分胸高断面积、蓄积量等都是构建林分生物量模型的重要预测变量,都反映了林分的密度状况。生物量与蓄积量高度相关,相较基于林分因子的模型,材积源模型具有更高的精度。
3)林分发育阶段对杉木人工林生物量有较大的影响,在构建林分模型时有必要考虑林龄的影响。
4)本研究所建模型具有较高的预估精度,各项误差均保持在合理范围内,适用于广东省杉木人工纯林或相对纯林,可在实践中推广。

