结合综合赋权与高斯区间隶属度的水电机组状态评价模型

秦小元，谢辉平，刘仁杰，徐 丹，刘 东，肖志怀

（1.向家坝水力发电厂，四川宜宾 644612；2.南京南瑞继保电气有限公司，南京 211101；3.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；4.武汉大学水力机械过渡过程教育部重点实验室，武汉 430072）

0 引 言

合理评估水电机组所处健康状态是保证机组安全稳定运行的重要环节，国内电站大多都已安装了实时有效的状态监测系统，通过对判断监测指标是否超限，确定机组实时运行状态。但目前状态监测多侧重对单一测点分析，未能很好的将单个监测指标劣化程度与对机组整体系统的影响联系起来。水电机组测点众多，且正常样本多，故障样本少，如何利用现有监测数据对机组进行全面有效的评估是水电领域需要深入研究的问题。

层次分析法作为一种经典的体系分析方法，由于结构清晰，层次分明，对复杂系统适应性强等特点，被广泛应用于风险评估，资源分配，设备评价等领域［1，2］，目前在水电领域上也有部分应用，如毛成等［3］利用层次分析法构建水电机组评价指标体系与评价模型，阐述了该方法在水电机组健康评价方面的应用，但使用层次分析法进行指标赋权存在过于依赖主观经验，客观性不足等问题，使得其在水电领域的应用更多停留在体系分层方面。

随着水电事业的不断发展，国内水电领域颁布了多种行业规则与电站运行规程用于确定机组监测量限值［4］，为机组运维检修提供指导参考，但水电机组类型繁多，运行环境复杂，监测指标尤其是快变量指标如振动类、摆度类、压力脉动类受机组自身运行工况，安装位置等因素影响较大，且不同工况范围内，监测指标适用的限值范围往往不同，这就使得单纯依赖行业导则规程难以有效确定机组各指标限值，对机组自身实际情况和积累的海量历史健康数据没有充分考虑。针对这一问题，部分学者通过分析机组监测样本的分布情况，提出使用基于高斯分布的阈值确定法计算机组监测量的限值［5，6］，这一方式相较于规程导则规定的单一报警值具有非常大的进步，为后续实现对水电机组更加精确的状态评价提供了可能。

本文针对当前水电机组状态评价方面研究的不足，在充分研究现有机组健康样本的基础上，提出了一种融合综合赋权与高斯区间隶属度的水电机组综合状态评价模型。根据研究对象结构和测点布置情况，利用层次分析法确定机组层次结构体系，计算各成分主观权重，根据监测系统历史数据，通过CRITIC法计算各成分客观权重，将主客观权重结合最终得到综合权重；其次，对机组额定工况下的历史健康样本进行统计分析，发现机组振摆类、压力脉动类等快变量信号峰峰值具有明显的正态分布特性，因此利用高斯阈值法确定机组各监测指标上下限值，对于温度等不符合正态分布特征的慢变量信号，根据现有行业规则确定其限值。将指标限值分为四个区间，并制定各区间得分体系。最后，判断实测指标所属区间的区间隶属度与指标分值，将指标分值加权得到系统总体分值，根据分值对应的状态等级判断机组所处运行状态。使用该评价模型对某电站机组进行了评价，结果表明该模型具有良好的评价效果。

1 水电机组层次分析体系构建

水电机组测点众多，且不同电站、不同类型机组测点布置形式不尽相同，就水轮机系统而言，监测量基本都可分为振摆类、压力脉动类、温度类等，为尽量真实反映机组运行状态，本文按照机组监测量类型构建层次分析体系，以某电站3 号机组为例，将该机组水轮机系统层次结构分为三层，如图1所示。

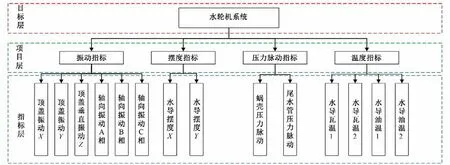
图1 水轮机系统层次结构体系Fig.1 The hierarchical analysis system of the turbine system

图1中所构建的层次结构体系由上至下分为目标层—项目层—指标层，涵盖振动、摆度、压力脉动、温度四大类监测指标，可较为全面反映水轮机系统的运行状态。

2 基于综合赋权与高斯区间隶属度的机组状态评价模型

该评价模型算法流程如图2 所示，模型总体分为离线和在线两个阶段。

图2 水电机组状态评价模型算法流程Fig.2 Algorithm flow of hydropower unit state evaluation model

离线阶段：①根据机组结构与测点布置情况，确定层次分析体系，将机组由上至下分为三层：目标层—项目层—指标层；②使用综合赋权法确定各层成分权重；③确定机组各指标运行限值，振动类指标根据其正态分布特性确定，温度类则根据现有规程导则和机组实际情况确定；④将指标限值分为4个区间，并制定各区间得分体系。

在线阶段：①根据指标限值，判断监测指标实时值所属状态区间，计算对应区间隶属度；②根据区间隶属度计算指标健康分值；③将各指标分值加权，计算项目层各成分分值；④将项目层分值加权，计算目标层分值；⑤根据各层得分情况对机组整体状态进行评价。

在层次分析体系中，底层指标权重对整体得分的影响会随着传递层数的增加不断衰减，出现类似于神经网络梯度消失的现象，如当底层某指标严重偏离正常值时，往往预示着系统已经出现异常，但在系统总体得分中可能并没有足够体现，整体评价结果依然正常。针对这一问题，有学者提出了变权理论［7］适当增加异常指标权重占比，使其能突出对评价结果的影响程度。变权理论在一个指标出现异常时，能够起到很好的变权效果，当同一子项目层下的多个指标异常时，则变权效果不理想［8］。水电机组这类复杂系统具有强耦合特点，各指标之间互相关联，单一指标出现异常并不能充分说明机组整体处于异常状态。综合以上考虑，本文将项目层得分作为评价机组系统整体状态的依据，项目层中子项目最低分所处状态为机组系统最终状态，且当同一子项目层下有50%及以上指标得分为异常时，判定机组系统异常。

3 综合赋权理论

在复杂系统中，各子成分权重分为主观权重和客观权重，其中主观权重从认识的角度出发，根据各成分之间的重要程度，依据行业共识或专家经验进行权重判定。客观权重则从系统本身出发，通过不同成分数据所反映的系统信息对各子成分进行赋权。主观赋权与客观赋权相互补充，共同反映了系统成分的真实权重。

在机械设备主观赋权方面，层次分析法能有效考虑各成分之间的相互影响，是最为常用的主观赋权方法，其核心是对复杂系统按照从整体到局部的原则进行层次分解，然后构造判断矩阵并求解矩阵最大特征根以及对应的特征向量，得出每一层指标权重w。

CRITIC（Criteria Importance Through Intercriteria Correlation）法［9，10］是一种客观权重赋权法，该方法以指标包含信息量作为确定指标权重的依据，指标信息包括同一指标之间的差异性以及该指标与不同指标之间的冲突性。指标差异性即指标变化幅度，变化幅度越大，表明指标差异性越大，一般用标准差表示。指标冲突性指该指标与其他指标之间的关联程度，冲突性越大，表明关联程度越低。CRITIC 法确定指标权重，不仅考虑了同一指标包含的信息量，还考虑了不同指标的相关性，使计算结果更加客观合理。运用CRITIC法确定指标权重步骤为：

（1）指标归一化。对于第i个监测指标Vi={Vi( 1) ，Vi( 2 )，…，Vi(t)，…，Vi(m)|i，t，m∈N+，对 其 进 行 归 一 化，去 除 指 标量纲：

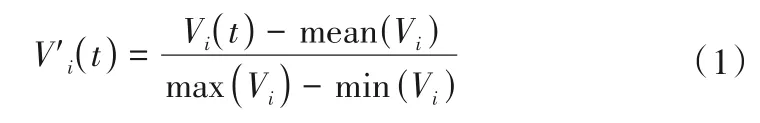
于 是 归 一 化 后 的 指 标 为：V′i={V′i( 1) ，V′i( 2 )，…，V′i(t)，…，V′i(m)|i，t，m∈N+}。

（2）计算指标信息量。在CRITIC 法中，指标信息包括指标差异性与指标冲突性，差异性用标准差表示，记为σi；假设指标Vi与指标Vj的皮尔逊相关系数［8］为rij，则指标Vi的冲突性K为：

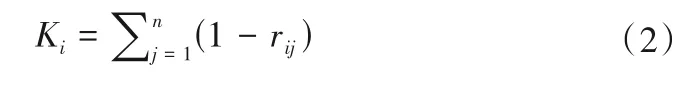
指标信息量Gi为：

（3）计算指标客观权重。将指标信息量归一化，得到各指标客观权重：

γ=(γ1，…，γn)T为指标客观权重向量。

将层次分析法求得的主观权重w与CRITIC 法求得的客观权重γ结合，求取指标综合权重ω。综合权重应尽可能接近主观权重与客观权重，而不偏重其中任意一项，本文依据最小鉴别信息原理［11］确定综合权重。计算方式为：

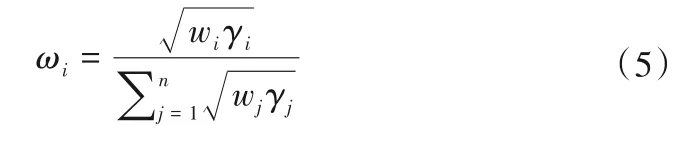
则综合权重向量：ω=(ω1，…，ωn)T。

4 机组指标区间状态评价

4.1 机组监测指标定量分析

水电机组监测指标多为定量指标，进一步的，定量指标又可分为越大越优型指标、越小越优型指标和中间型指标。本节引入劣化度概念，表征机组当前实际状态与故障状态相比的相对劣化程度，其取值范围为［0，1］。不同取值反映评判指标不同的劣化程度。

对于越小越优型指标，劣化度计算式为：

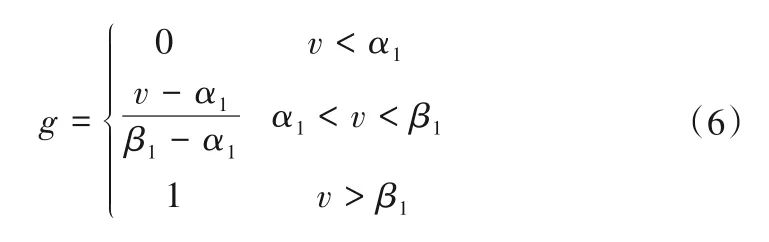
式中：g为评判指标的劣化度；v为指标实测值；β1为指标上限值；α1为指标最优值，且α1＜β1。

对于越大越优型指标，劣化度为：

式中：α2为指标下限值；β2为指标最优值，且α2＜β2。

此外机组还存在中间型指标，中间型指标本质上属于越小越优型指标与越大越优型指标的集合，当指标值位于最优值左区间时，指标为越大越优型指标，右区间则为越小越优型指标。

4.2 机组监测指标统计分布分析

在水电机组测点信号中，振动类信号属于快变量信号，这类信号主要特征是随时间变化较快，具有较快的周期变化规律，但在测量上又有着较强的随机误差，振动信号的分布特性已有学者进行过研究，研究表明振动信号峰峰值分布具有明显的正态分布特性。但对于温度这类随时间变化较慢的慢变量信号，目前尚未有研究表明其也具有正态分布特性。以第2 节机组为例，对该机组额定运行工况下某正常时段内的顶盖Z向振动，水导X向摆度、蜗壳压力脉动、水导轴承瓦温信号进行统计分析，验证其是否符合正态分布，结果如图3所示。

从图3（a）～（c）可以看出，机组顶盖振动、水导摆度和压力脉动数据比较接近高斯分布，可认为该类数据近似符合高斯分布，水导瓦温则明显不服从高斯分布，且不遵循任何一种明确的数学分布。因此可以认为，在当前同一工况下，机组振动类信号峰峰值序列符合高斯分布，温度类不符合高斯分布。

4.3 基于高斯分布的监测指标阈值确定

假设x～N(μ，σ2)，则x的概率分布函数为：

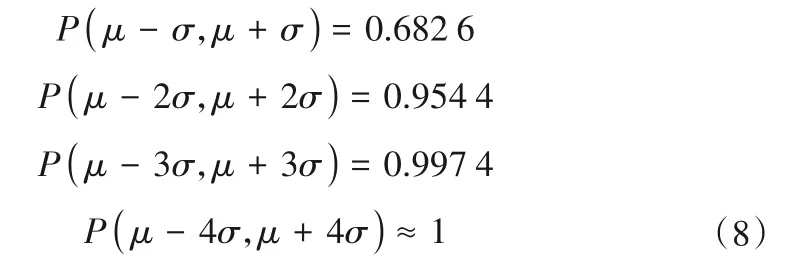
由于水电机组振动监测指标具有明显的正态分布特征。对于机组某监测指标Vi={Vi(1)，Vi(2)，…，Vi(t)，…，Vi(m)}，根据式（8），该指标任一组实时监测值Vi(t)落在区间[μ- 3σ，μ+3σ]的概率为99.74%，落在区间[μ- 3σ，μ+ 3σ]外的概率为0.26%，属于小概率事件，在水电机组正常运行中，小概率事件几乎不可能发生，因此将[μ- 3σ，μ+ 3σ]作为机组监测指标正常运行限值，即3σ法则［5］。当监测指标幅值超过[μ-3σ，μ+ 3σ]时，则认为该指标出现异常。为更加全面细致衡量指标状态，在3σ法则基础上，将指标限值进一步延拓，根据式（8），确定[μ- 4σ，μ+ 4σ]为机组振动指标总体限值，μ为最优值，其中：

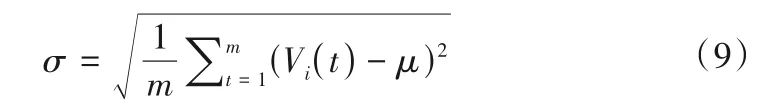
4.4 基于区间隶属度的监测指标劣化评价

将机组及指标评价状态分为4级，分别为状态I：良好，状态II：合格，状态III：注意，状态IV：异常。机组各状态评价等级对应分值如表1所示。

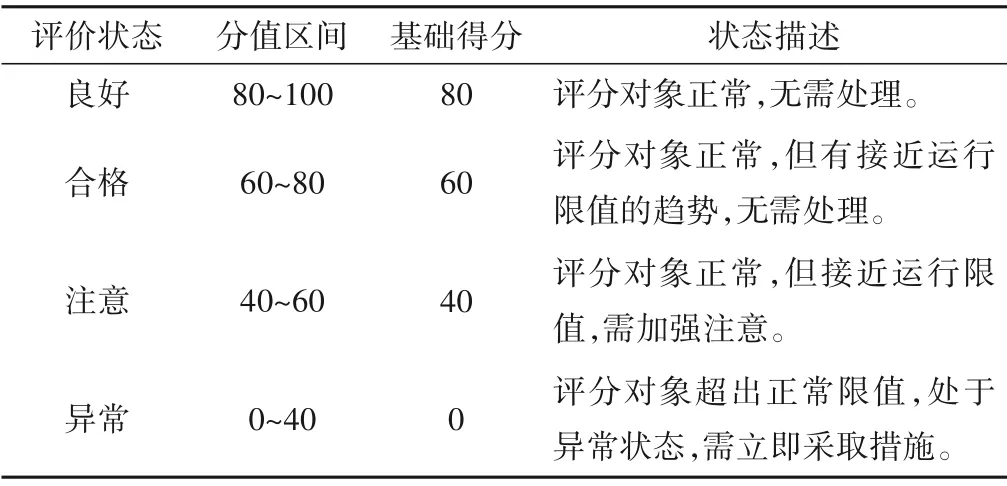
表1 水电机组状态评价表Tab.1 Hydropower unit state evaluation table

相应的，根据状态分级，将指标限值分为对应的四个区间，分 别 为：良 好：[μ-σ，μ]∪[μ，μ+σ]，合 格：[μ- 2σ，μ-σ]∪[μ+σ，μ+ 2σ]，注 意：[μ- 3σ，μ- 2σ]∪[μ+ 2σ，μ+3σ]，异常：[μ- 4σ，μ- 3σ]∪[μ+ 3σ，μ+ 4σ]。当指标监测值位于某状态区间的右段时，该指标为越小越优型指标，劣化度计算如式（6），否则为越大越优型指标，劣化度计算如式（7）。

定义隶属度概念，用于衡量指标在所属状态区间隶属程度，隶属度l计算方式为：

从式（10）可以看出，指标区间隶属度与劣化度互为相反关系，当隶属度越大，表明该指标值在当前所属状态区间内劣化度越小，反之越大。

根据指标区间隶属度计算指标健康得分，指标得分计算方式为：

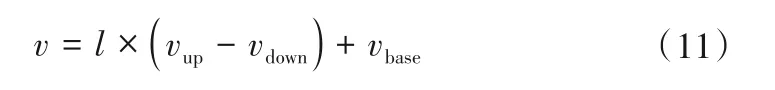
式中：v为指标得分；vup为指标所属状态区间上限分值；vdown为下限分值；vbase为基础分值。

如当指标实时值为良好状态区间，则根据表1，有vup= 100，vdown= 80，vbase= 80。

根据各指标权重对各指标得分加权求和，即得到上一层分值。

5 实例验证

以第1 节所分析的电站机组为例，使用该模型对机组不同时刻下的运行状态展开评估。机组额定工况为200 MW，在2015年8月底发生了转轮室里衬脱落故障，期间机组一直满负荷运行，由于机组转轮属于水轮机系统，因此对水轮机系统状态展开分析，其层次结构如图1所示。

文献［12］基于轴向振动信号对该机组在故障发生前后的运行状态进行了详细分析，根据分析结果可以判断机组在8月20 号之前处于正常运行状态，因此选取8月10 号-20 号时间段内每个测点各200 组数据作为正常样本，用于计算指标权重与指标限值。

5.1 层次体系权值计算

5.1.1 指标层权重计算

使用层次分析法计算指标层各指标主观权重，根据图1，振动类指标包括6个指标，主观认为各指标重要程度相同，因此振动指标主观权重向量为(1 6，1 6，1 6，1 6，1 6，1 6)T。同理，摆度类各指标主观权重向量为(1 2，1 2)T，压力脉动指标主观权重向量(1 2，1 2)T，温度指标主观权重向量(1 4，1 4，1 4，1 4)T。以各测点正常数据作为计算样本，使用CRITIC 法计算各指标客观权重，最终将主客观权重带入式（5）得到指标综合权重向量如表2所示。

表2 指标层权重向量Tab.2 Index layer weight vector

5.1.2 项目层权重计算

使用层次分析法确定项目层各类别指标权重，振动、摆度、压力脉动指标为快变特征量，对机组状态的反映更为敏感，因此在重要度上振动指标=摆度指标=压力脉动指标＞温度指标。通过层次分析法确定项目层权重为：ω=（0.285 7，0.285 7，0.285 7，0.142 9）T。

5.2 监测指标限值计算

根据4.2 节分析结果，同工况下的快变量信号存在高斯分布特性，振动、摆度、压力脉动指标限值根据4.3 节方法确定，将各指标正常样本带入式（8），得到指标总体限值如表3所示。

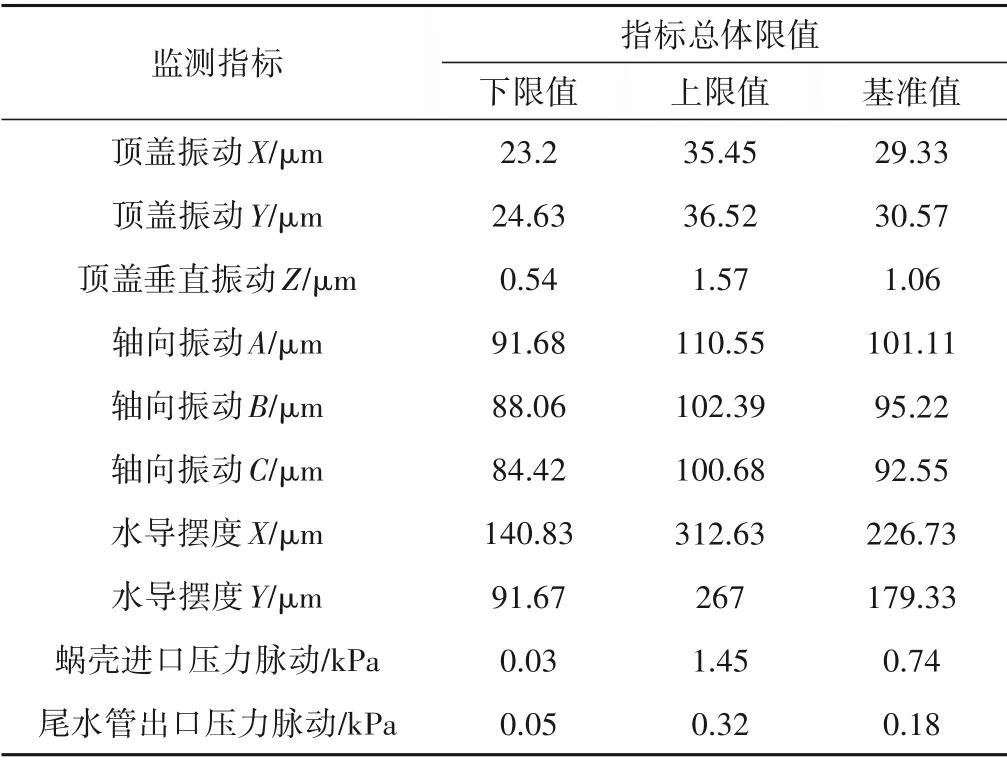
表3 快变量指标限值Tab.3 Fast variable index limit

温度指标由于不符合高斯分布特性，因此通过高斯分布确定阈值的方法不再适用，根据GB/T 7894-2009《水轮发电机基本技术条件》中对水轮发电机组导轴承温度的规定如表4所示。

表4 轴承允许温度值 ℃Tab.4 Allowable bearing temperature

所评估机组水导轴承轴瓦为巴氏合金瓦，正常情况下最高温度限值为75 ℃。综合考虑电站规程与行业导则，确定水轮机系统温度类指标限值如表5 所示。在各状态范围内，温度指标均为越小越优型指标。

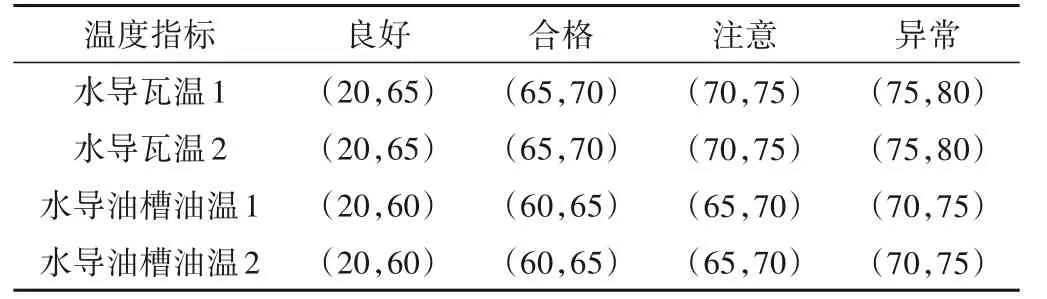
表5 水轮机系统温度类指标限值Tab.5 The turbine system temperature index limit

5.3 机组状态评估

文献［12］通过构建基于机组轴向振动信号的劣化指标，分析了该机组由正常到故障的演变过程，劣化指标随时间的变化趋势如图4所示。

图4 机组劣化指标变化趋势图Fig.4 Change trend chart of unit degradation index

根据文献［12］的分析结果，将指标大于0.2 认为是故障开始的标志。选取A、B、C、D四个有代表性时刻点，使用所构建的状态评价模型对各时刻点机组水轮机系统状态进行整体评价，各时刻点指标监测值如表6所示。

表6 额定工况下机组水轮机系统监测数据Tab.6 Monitoring data of the turbine system under rated conditions

表7 为各时刻水轮机系统详细得分情况。A 时刻水轮机系统各项指标得分均处于正常水平，机组无异常；B时刻振动指标中轴向振动指标A、B、C 相均出现异常，且振动指标处于注意状态，此时机组发生故障的可能性较高，需加强注意；C 时刻振动指标中50%指标异常，振动指标评分为异常，机组故障；D 时刻机组故障进一步发展，此时振动指标中超过50%指标异常，且水导摆度指标也出现异常，机组故障征兆明显，需立即停机。对比图4，可以发现A 时刻机组劣化度维持在很低水平，此时机组整体正常，B 时刻机组出现劣化趋势，C 时刻机组劣化指标突破0.2，认为机组出现故障。该模型分析结果与图4 结果相同，不同的是图4 劣化指标侧重于反映机组是否故障，而评价模型则更精细的评价机组状态。

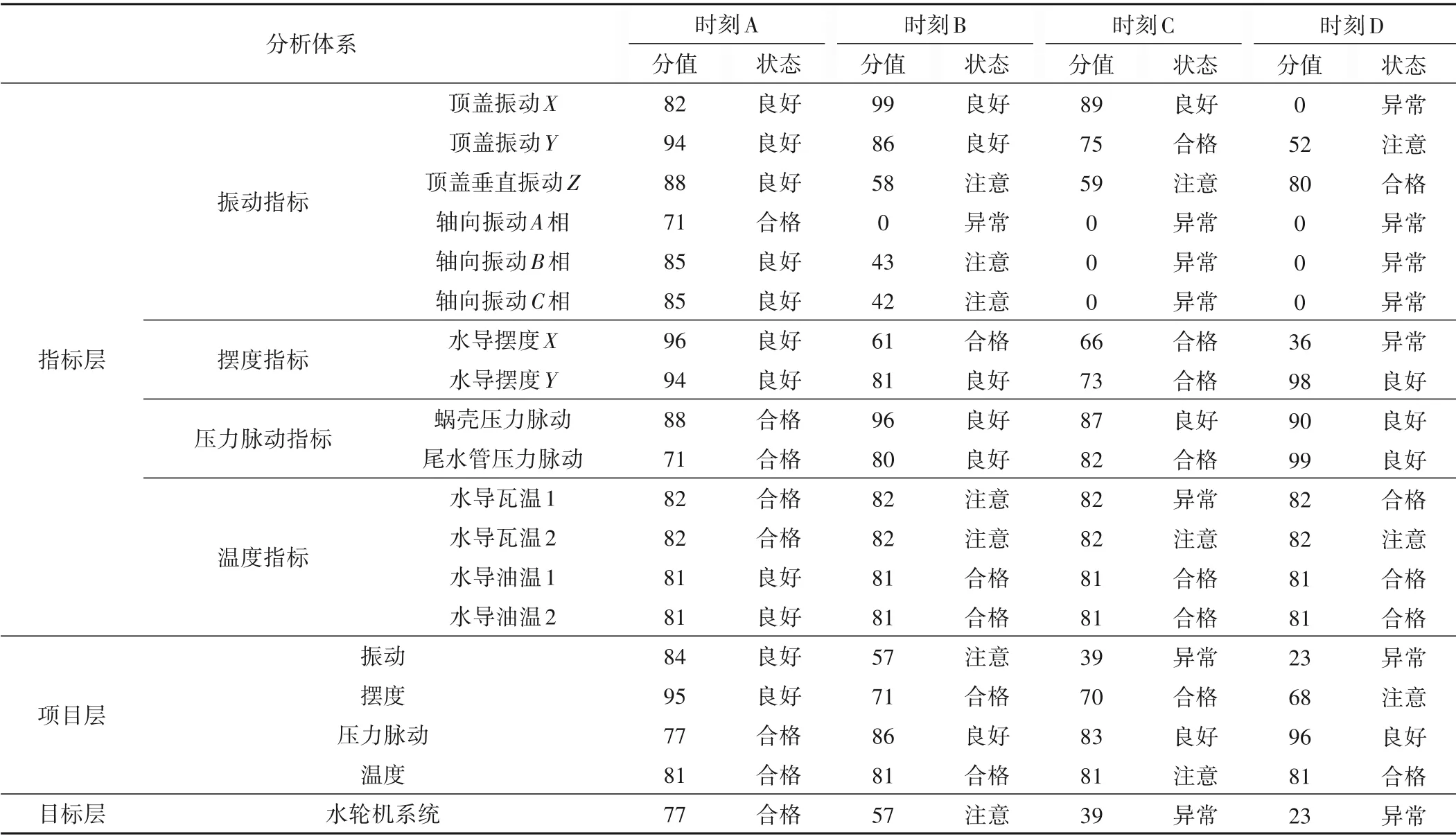
表7 水轮机系统详细分值Tab.7 Detailed score of hydraulic turbine system

6 结 论

针对目前水电领域缺乏有效完善的设备整体状态评价方法，本文在分析了机组监测样本统计分布的基础上，结合综合赋权理论和概率论，构建了一种水电机组状态评价模型，以水轮机系统为实验对象，验证了该模型可有效准确判断机组所处运行状态，能为机组状态监测与故障预警提供有效支持。本文主要结论与特色如下：

（1）使用层次分析法与CRITIC法确定机组各子项目主客观权重，在尊重专家经验同时，考虑了历史监测数据，使得权重结果更为合理。

（2）对现有机组历史健康样本进行分析，得出在同一工况下，快变量指标符合高斯分布，温度指标不符合高斯分布。并根据这一结论改进3σ法则，确定快变量指标阈值范围，对阈值进行分段，使得对机组指标和机组整体的评判更加精细化。

（3）针对层次分析体系中底层指标权重传递衰减现象，提出将中间层得分作为评价机组系统整体状态的依据，并结合各类指标具体得分情况确定机组最终状态，有效解决依赖变权方式不能准确体现多个异常指标对设备整体状态影响程度的弊端。