梯级橡胶坝塌坝调度及泄流特性数值研究

张倩楠，周 敏，郝瑞霞，胡孜军，田 淳

（1.太原理工大学水利科学与工程学院，太原 030024；2.重庆开物工程咨询有限公司，重庆 401122）

0 引 言

近年来，许多城市为改善城区生态环境和人居环境，进行了河道美化工程建设，在河道上修建多级橡胶坝，实现层级蓄水，形成良好的城市景观［1］。但汛期不合理调度会造成洪水叠加，影响下游安全，因此确定合理的闸坝调度策略显得尤为重要［2］。

对于橡胶坝调度运行，诸多学者根据工程运行管理经验及存在问题［3，4］提出运行方式，或是对橡胶坝塌坝泄流量的计算［5-7］进行研究分析。部分学者基于常规调度理论，利用程序搭建模型进行调度寻优，如邓浩等［8］采用改进遗传算法，从基本试算转向智能优化，寻求全局最佳调度方案；张庆华等［9］编制梯级橡胶坝塌坝泄流仿真系统，对不同调度方案塌坝过程及塌坝泄量进行预测；赵瑜琪等［10］综合考虑塌坝时间及速度，对突发汛情的应急调度方案展开研究等。上述调度方案的研究大都采用一维模型，对完全塌坝泄空的情况进行探索。对于大频率洪水，需要提前塌坝泄空以保证安全行洪，而对于较小频率洪水，塌坝泄空会造成水资源浪费，不利于洪后蓄水。目前对不完全塌坝的研究较少［11］。

本文以汾河太原城区段7 座橡胶坝为研究对象，本着安全行洪和蓄水兼顾的原则，进行小频率洪水不完全塌坝方面的研究。由于该段河道建筑物布置比较复杂，平面上有浑水渠和蓄水渠，加之橡胶坝、中隔堤和闸墩等，一维模型不能很好地反映这些建筑物的特点，而平面二维模型理论上可以有效地描述建筑物附近河道水流形态以及局部建筑物对水流的影响，且这方面研究成果有限。故利用MIKE21软件建立能考虑塌坝过程的二维水动力学模型，分析20%频率洪水来临时橡胶坝不同塌坝方案泄水过程，以期为工程调度提供一定参考。

1 计算原理

1.1 控制方程

平面二维水动力学模型将雷诺时均的Navier-Stokes 方程进行深度平均，形成二维浅水运动方程，考虑紊动引入涡黏性系数，同时也考虑风应力和科氏力作用，其方程如下：

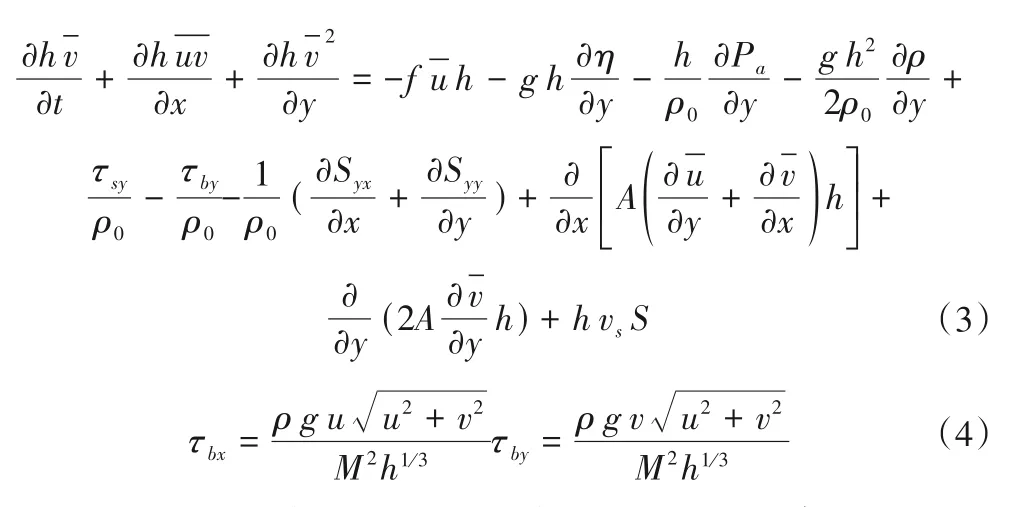
式中：h=η+d，为总水深，m；η表示水面到基准面的高度，m；d为静水深，m；S为点源流量，m3/s；u˙、v˙为基于水深平均的流速，m/s；us、vs为点源在x、y方向上的水流流速，m/s；g为重力加速度，m/s2；A为涡黏性系数，m2/s；ρ为水的密度，kg/m3；ρ0为水的相对密度，kg/m3；pa为当地大气压强，Pa；f=2ωsinφ为科氏力系数；φ为地理纬度；ω为地球自转角速度，rad/s；Sij为辐射应力分量，N/m2；τsx、τsy为表面风应力，N/m2；τbx、τby为河床底部应力分量，N/m2；M为曼宁系数，m1/3/s。

1.2 数值解法

计算区域划分为不重叠的三角形及四边形单元。采用有限体积法对控制方程进行离散，变量位于单元中心，跨边界通量垂直于单元边，用近似Riemann 解法求得单元界面的对流通量。时间积分采用了低阶显式Euler方法。

2 模型构建

2.1 模拟范围

模拟范围选择为汾河兰村至二坝段，全长约52 km，平均河宽约350 m，计算域面积18.371 km2。其中太原城区段为重点研究区域，河道平均底坡0.082%，有十条支沟汇入，经一二期综合治理后，共修建7 座橡胶坝，形成6 个蓄水池。橡胶坝工程区域建筑物和河道地形资料来源于具体设计报告及相关图纸，其余河段基于分辨率为30 m 的DEM 数据进行插值，模拟区域见图1。

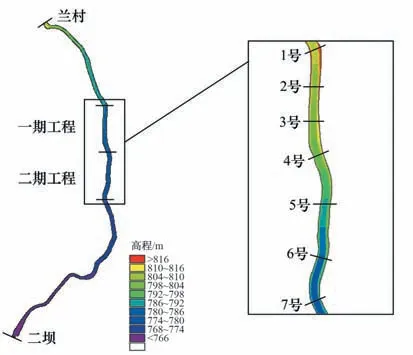
图1 模拟区域和橡胶坝布置Fig.1 Simulated area and rubber dam arrangement

一期工程总长近6 km，每隔2 km 设一橡胶坝，共有1～4 号4 座橡胶坝，1 号橡胶坝前断面尺寸见图2 所示；二期工程在一期工程基础上向南延伸7.6 km，有5～7号3 座橡胶坝。1～5号橡胶坝之间采用分槽蓄水，由中隔堤将河槽分为浑水渠和蓄水渠，当泄水流量较小时，由浑水渠下泄，流量较大时，蓄水渠塌坝过流；5～7号橡胶坝之间为全槽蓄水。

图2 1号橡胶坝处河道横剖面Fig.2 Cross-section of the river at No.1 rubber dam

2.2 网格划分

研究区域主河道和中隔堤处采用三角形非结构化网格，其中河道网格面积300～1 000 m2之间，中隔堤网格面积5.5～13 m2；橡胶坝附近区域采用四边形网格，网格尺寸为8 m×8 m。模型共生成网格88 130 个，图3 为1 号橡胶坝处局部网格示意图。

图3 1号橡胶坝处网格划分Fig.3 Grid division at No.1 rubber dam

2.3 初始条件及边界条件

初始条件采用初始时刻的恒定流水位和流量。

模型上游边界条件给定兰村流量变化过程，下游边界条件给定汾河二坝水位—流量关系。模型应用时边界条件设置如图4所示。

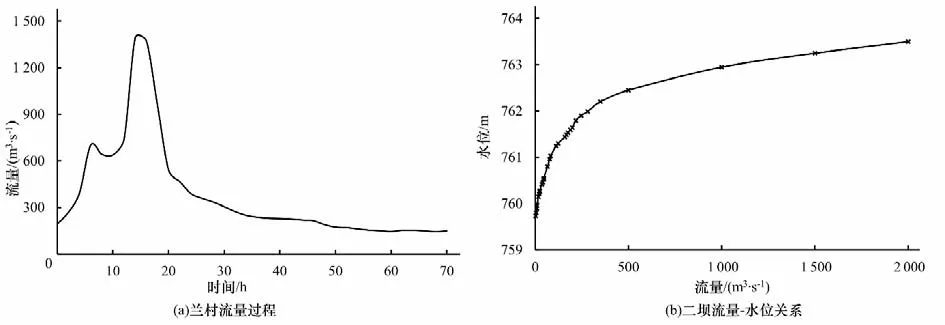
图4 模型边界条件设置Fig.4 Model boundary condition setting

2.4 参数设置

曼宁系数M：利用观测资料，通过数值验证进行参数率定，最终选定M=35 m1/3/s。

涡黏性系数：采用Smagorinsky公式，取0.28 m2/s。

科氏力系数：根据所处地理纬度推求，为8.95×10-5。

模型计算过程中时间步长取1 s。

3 模型验证及参数率定

3.1 橡胶坝模拟效果校核计算

模型中橡胶坝处流量采用Villemonte 堰流公式计算，其描述如下：

式中：q为通过堰的流量，m3/s；W为宽度，m；C为堰流系数；k为堰指数；Hus为上游水位，m；Hds为下游水位，m；Hw为堰顶高程，m，堰顶高程等于堰底高程加堰高。

为了分析模型计算所用公式（5）的合理性，本文选择工程区3种典型坝高：2.5、3、4 m 的橡胶坝进行矩形水槽橡胶坝控水效果的验证分析。计算不同水位不同塌坝高度泄流量所得流量系数，与文献［12］中模型试验数据进行对比分析，率定公式中参数C取值的合理性。模型计算结果见图5，模拟所得流量系数与文献平均相对误差为0.51%，认为模拟结果可行，公式中堰流系数C选取1.838。

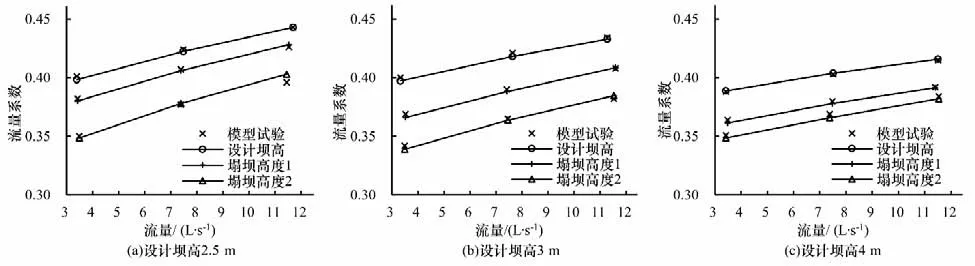
图5 不同坝高流量系数验证结果Fig.5 Verification results on flow coefficient of different dam heights

3.2 河道恒定流水面线模拟计算

为率定模型曼宁系数，考虑橡胶坝全塌，泄流量为2 000 m3/s 的情况，进行河道恒定流水面线计算。将模型水面线计算结果与传统算法进行比较分析，城区段河道水面线计算结果见图6所示，两者水深最大相对偏差4.56%，平均相对偏差2.23%，结果良好，模型曼宁系数选定35 m1/3/s。

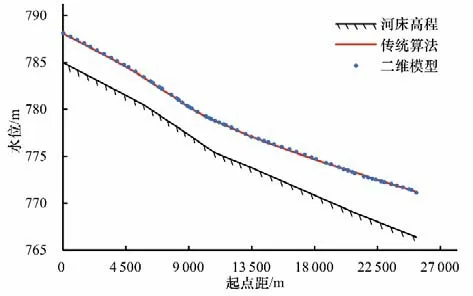
图6 恒定流水面线计算结果Fig.6 Constant flow water surface line calculation results

3.3 洪水演进过程模拟结果验证

选取模拟河段2016年7月19日0∶00至21日0∶00的水文资料及橡胶坝塌坝运行数据进行模拟结果验证计算。河道水文资料基于上下游测站实测数据，各支流由控制流域面积采用类比的方法插补延展得到；橡胶坝塌坝运行实际过程见图7-9（a）。1 号、6 号及7 号坝前水位和流量变化过程计算结果与实测过程对比见图7-9（b）、（c）所示。计算得各坝前水位平均相对偏差2.38%，流量平均相对偏差9.2%，验证结果良好。

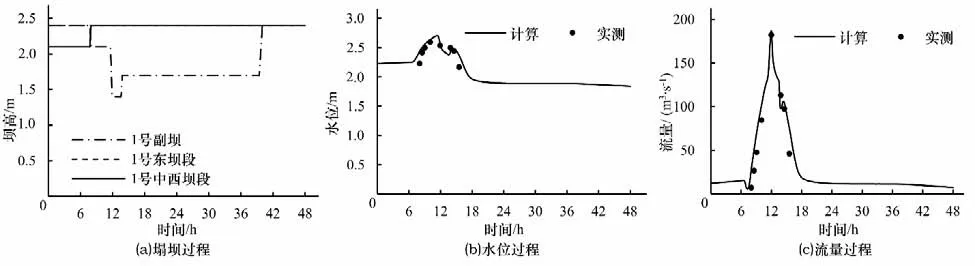
图7 1号橡胶坝模型验证Fig.7 Validation results at No.1 rubber dam

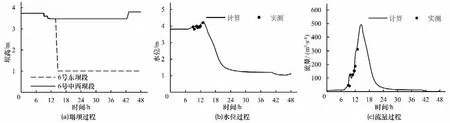
图8 6号橡胶坝模型验证Fig.8 Validation results at No.6 rubber dam

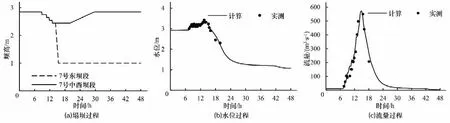
图9 7号橡胶坝模型验证Fig.9 Validation results at No.7 rubber dam

4 模型应用

4.1 计算方案

选择研究区域20%频率洪水（洪峰流量为1 394 m3/s）过程线作为来水条件，分析7 座橡胶坝在不同塌坝组合情况下的过流特性。以洪水能在主河槽内安全行洪和节约水资源，同时利于洪后蓄水为前提，根据河道过流能力及洪峰流量进行初步计算，设计4种塌坝组合方案，进行洪水演进模拟。当上游来流小于500 m3/s（浑水渠设计泄量）时，洪水直接通过浑水渠下泄；上游来流量大于500 m3/s时蓄水渠侧开始塌坝。各坝塌坝高度如表1所示，塌坝速度按照设计标准为0.03 m/min。

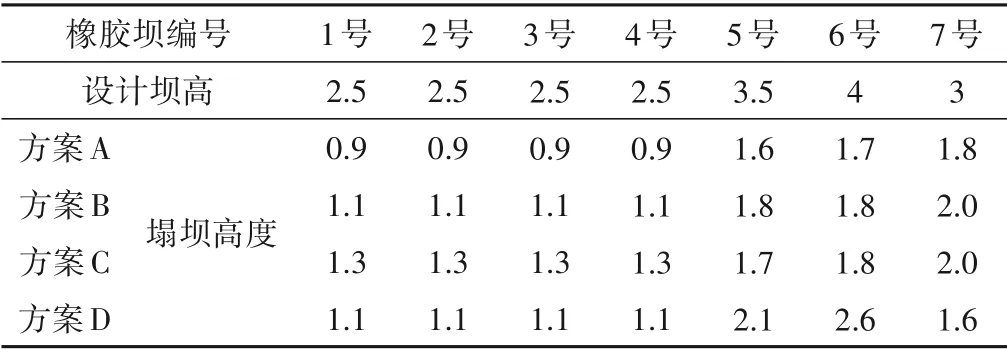
表1 橡胶坝塌坝计算方案 mTab.1 Calculation scheme of rubber dam collapse

4.2 方案计算结果分析

4.2.1 洪水演进过程分析

河道中洪水以波的形式传播，当发生20%频率洪水时，4种塌坝方案洪水演进过程类似。洪峰由兰村到达1号橡胶坝处约3 h，到达7 号坝约4 h，到达二坝处约8 h。图10 为典型方案特征断面流量随时间变化曲线，可知，洪水在传播过程中，洪峰逐渐坦化，兰村处洪峰流量为1 394 m3/s，到1 号橡胶坝处为1 381 m3/s，到达二坝处，约1 256 m3/s。

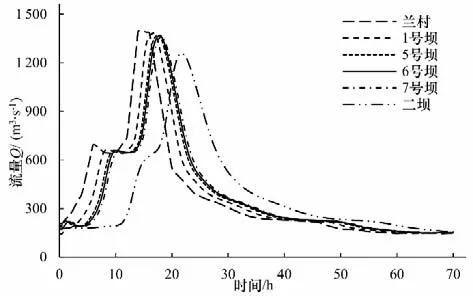
图10 典型方案特征断面流量过程线（方案B）Fig.10 Flow process of characteristic section in typical scheme（scheme B）

但不同塌坝方案下，洪水通过时1 号橡胶坝处流量分配情况不同，表2为洪峰通过1号橡胶坝时流量分配情况。随着1号橡胶坝的塌坝高度的增大，阻水能力减弱，蓄水渠分配流量增大，浑水渠分配流量随之减少。

表2 1号坝浑水渠及蓄水渠流量分配Tab.2 Flow distribution of muddy channels and storage channels of No.1 dam

为保证洪水能在主河道内安全通过，洪峰到达时，各橡胶坝工程区内水位应低于内堤高程，对各塌坝方案下橡胶坝处最高水位线进行比较分析，绘制图11 所示各方案最高水位包络线图。

图11 不同方案工程区最高水位包络线图Fig.11 The highest water level envelope diagram in the project area under different schemes

方案A 中，洪峰通过时，浑水渠侧水位均低于内堤高程，蓄水渠侧水位略高于内堤高程，1号坝前水位超出内堤高度较大，为0.06 m；方案B 与方案C 中，洪峰通过时浑水渠侧及蓄水渠侧水位均低于内堤高程，且方案C 中浑水渠侧水位低于中隔堤高程；方案D 中，各橡胶坝塌坝高度相同，下游橡胶坝对上游顶托作用较弱，除7 号橡胶坝外，各处水位均低于内堤高程。综上，方案B与方案C均满足安全行洪要求。

4.2.2 工程区流场特性分析

工程区1 号坝和5 号坝处为中隔堤始端和末端，均有绕流现象出现，图12 和图13 为典型方案不同时刻1 号和5 号坝处局部流速矢量图。T=17 h 和18 h 分别为1 号坝和5 号坝相应洪峰出现时刻，相较而言此时绕流现象不大明显，如图12 和图13（b）所示。在流量较小时刻，洪水多由浑水渠下泄，1 号坝和5号坝处出现明显的绕流现象，如图12和图13（a）（c）所示。

图12 典型方案不同时刻1号橡胶坝处流速矢量（方案B）Fig.12 Velocity vector at No.1 rubber dam of typical scheme at different time（scheme B）

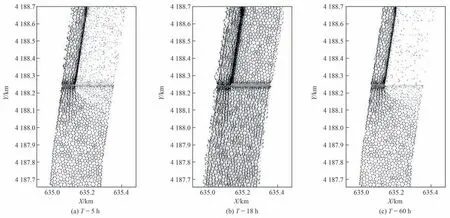
图13 典型方案不同时刻5号橡胶坝处流速矢量（方案B）Fig.13 Velocity vector at No.5 rubber dam of typical scheme at different time（scheme B）

4.2.3 方案比选分析

经上述分析可知，方案B与方案C均能满足安全行洪要求。综合考虑洪后蓄水，方案B塌坝高度较小，虽局部稍有漫过中隔堤现象，但未漫上内堤，既能满足行洪要求，也更利于洪后蓄水，避免水体浪费，为较优方案。

方案B 洪峰通过时，各坝前断面特征参数见表3所示，表中ΔZ1为坝前水位超出内堤高度，ΔZ2为坝前水位超出中隔堤高度。1～5 号坝分槽蓄水，其中1～4 号坝的设计坝高、塌坝高度及河道底坡均相同，故在蓄水渠侧水深和流速大致相当，水深3.12～3.25 m 之间，流速1.14～1.16 m/s 之间；在浑水渠侧，由于4号～5 号橡胶坝间底坡最陡，且5 号坝在中隔堤末端，洪峰通过时此处水深最小，流速较大，可达2.68 m/s。6 号橡胶坝立坝高度最大，为全槽蓄水，此处水深较大，最大4.11 m，流速1.07 m/s。

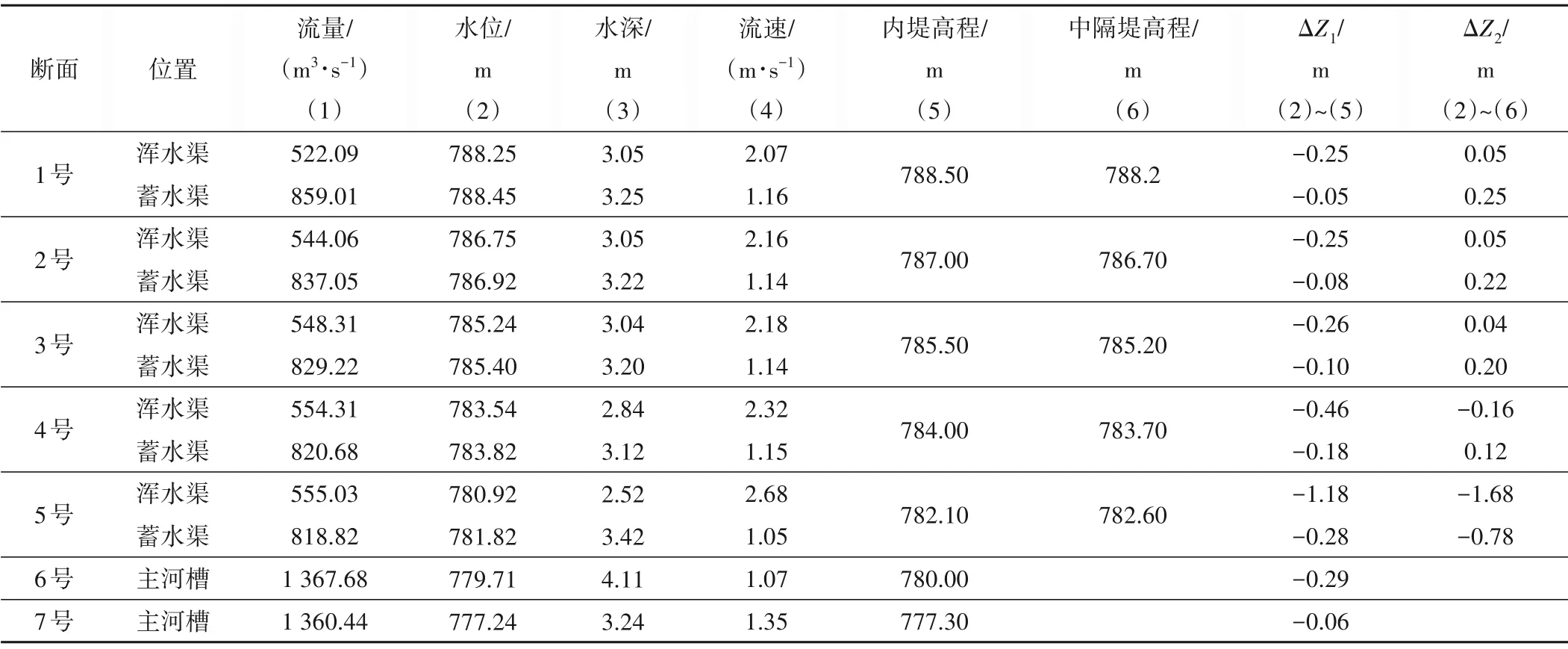
表3 方案B洪峰通过时坝前断面特征参数汇总表Tab.3 Summary of the characteristic parameters of the pre-dam cross-section during the passage of the flood peak of Scheme B

5 结 论

本文以汾河上兰村至二坝段为分析对象，构建了考虑橡胶坝塌坝过程的二维洪水演进模型。在模型验证的基础上，针对小频率洪水，对不完全塌坝组合方案进行对比分析，主要结论如下：

（1）通过对橡胶坝模拟效果进行校核，发现堰流系数C取1.838 合理，计算所得流量系数与试验比较，平均相对偏差0.51%。通过对河道进行恒定流水面线模拟计算，曼宁系数选定35 m1/3/s，城区段河道水深平均相对偏差2.23%。在此基础上进行了考虑橡胶坝调度过程的实际洪水演进过程模拟验证工作，计算所得各坝前水位和流量过程与实测过程比较，水位平均相对偏差2.38%，流量平均相对偏差9.2%，吻合良好。

（2）选择研究区域20%频率洪水过程作为来水条件，分析7座橡胶坝在4 种不完全塌坝组合情况下的过流特性，得出以下结论：洪水以波的形式传播，且传播过程中洪峰逐渐坦化，20%频率洪水到达工程区1 号坝前约3 h；1 号橡胶坝的塌坝高度与蓄水渠内的流量分配呈正相关关系；1 号坝和5 号坝分别为中隔堤始端与末端，会发生绕流现象，特别是流量较小时，大部分由浑水渠下泄，绕流现象愈加明显；基于安全行洪及节约水资源的原则，对4 组塌坝方案下洪水通过工程区的过流特性进行分析，方案B 为最优方案，其1～7 号坝的塌坝高度分别为：1.1、1.1、1.1、1.1、1.8、1.8、2 m。上述结论有助于太原城区发生低频率洪水时橡胶坝运行规则制定提供参考，同时可为类似工程的模拟分析提供参考。