基于SWMM与NSGA-III的城市排水系统多目标优化
刘 军,高徐军,焦永宝,薛树红,吕 鹏,杨 霄,康 抗,韩靖博
(1.中电建路桥集团有限公司,北京 100160;2.中电建西北勘测设计研究院有限公司,西安 710065)
0 引 言
受气候变化以及城市化进程加快的影响,我国城市内涝现象频发,城市在应对内涝问题上面临巨大挑战[1-3],城市雨排水系统的设计及运维对缓解城市内涝尤为重要。在海绵城市建设背景下,除了最初的雨水管网系统,城市雨排水系统还引入了雨水花园、植草沟、生物滞留带、绿色屋顶等绿色设施来消纳径流雨水,但绿色设施调控能力有限[4,5],对于中、大重现期降雨,城市雨水仍需借助灰色排水设施进行排放。灰色排水设施主要有由含调蓄池在内的雨水管网系统构成,但受到其水力特性、当地发展战略以及经济成本等因素的限制,导致其在实际工程应用中受限。常规的城市雨水排水系统设计主要是通过情景模拟与数学规划等方法结合,模拟设计降雨条件下的不同管网布设场景,评估城市排水系统的设计效果。然而该类方法过于依赖设计人员的经验或既定条件下的某种线性设计,不仅效率低下并且影响设计方案的最优性。
针对传统设计方法难以满足目前的排水系统设计要求问题,相关学者就排水系统优化和算法进行了大量研究[6-8]。这些优化算法主要有遗传算法、粒子群算法、人工神经网络和组合算法模型等[9-11]。王永华等[12]以经济效益单一目标为最小为目标,采用遗传算法对管网进行优化设计,该方法难以获悉同等经济投入条件下内涝防治效果的提升。郑恺原等[13]以管网经济成本、排涝有效性和积涝风险共同作为优化目标,基于SWMM 构建多目标优化模型;徐得潜等[14]基于雨水管道年费用、管网脆弱度和溢流量3 个目标,构建多目标优化模型;李芊等[15]以管径与检查井的内底标高为优化变量,以建设成本和雨水系统节点溢流量为目标,构建基于粒子群算法的多目标优化模型,以上学者将管道承载力、内涝防治效果和经济成本为目标进行优化,忽略了城市雨水管网系统中应对中、大雨条件下调蓄池设计相关的优化。郑旭强等[16]着眼于提升内涝削减效果和加快排水,将调蓄池引入优化对象,以管道的修复或更换、调蓄池的位置及大小等作为决策变量,开展排水管网优化设计,忽略了调蓄池对雨水的蓄存的作用。
以西安市小寨区域城市雨洪系统为例,兼顾经济成本、内涝防治和雨水滞蓄目标,通过排水管网和调蓄池2 种灰色排水设施的整体性设计,结合城市洪涝风险最低、经济投入最小和蓄水量最大的3个目标,提出了一种基于SWMM 模型和NSGAIII 算法的多目标排水系统优化方法。该方法利用SWMM 模型模拟不同方案的降雨径流过程,并通过动态链接库(DLL)为优化算法提供节点的溢流量、经济投入和径流控制信息;NSGAIII算法则寻找城市排水系统设计方案中的最优帕累托(Pareto)解集,从而能够最大限度的保证各目标之间的独立性和解的收敛性。结合西安市小寨区域排水分区建模实例,对该方法的可行性和有效性进行了测试和分析,并对排水系统优化效果进行了分析。
1 优化模型开发
在海绵城市的建设理念中,排水系统的建设应不仅要考虑实际排水能力与经济投入,还要考虑雨水利用率,通过调蓄池的蓄存可将更多的雨水进行回收利用。本文所提排水系统优化模型的目标函数包括溢流量函数F1,经济成本函数F2和径流控制函数F3,即:
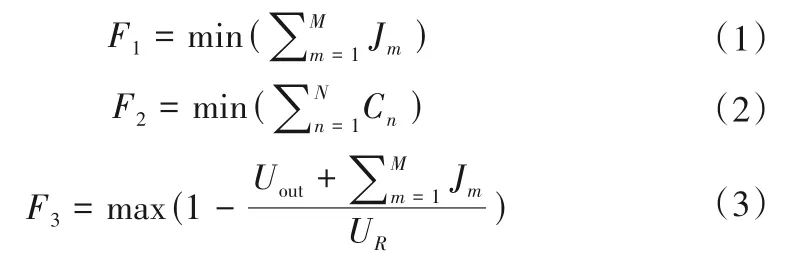
式中:M为研究区域的总节点个数;Jm为第m个节点的溢流量,由SWMM 计算得到;N为待优化管段数量;Cn为第n根管道的经济成本;Uout为雨水管网系统的外排量;UR为区域降雨总量;其中Cn的计算公式为:

式中:Ln为第n根排水管道长度;W(Dn)为单位管道长度费用。
约束条件包括总管道流速、管径大小、调蓄池体积约束,即:
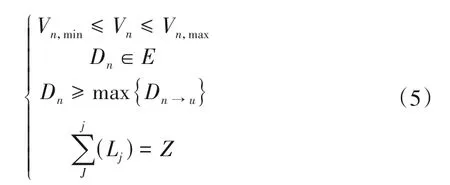
式中:Vn为第n个排水管道的设计流速[17];Vn,min和Vn,max分别为该管道的最小和最大流速,分别取为0.75 和5 m/s[17];Dn为第n个排水管管道直径;E为当地可以选择的范围管径;MAX(Dn→u)为第n个排水管上游最大管径;J为区域内调蓄池总数量;Lj为第j个调蓄池的体积;Z为调蓄池总体积;其中Vn的计算公式为:

式中:η为管壁的粗糙系数;Rn是第n根管道的水力半径,水力半径为恰好满流时的水力半径,取值为D/4;In为第n根管道的坡度,计算公式如下:

式中:Hn→u和Hu→n分别为连接第n根管道上下游节点的节点底高程,相邻两节点的底高程决定了该段管道的坡度。
2 模型求解算法
NSGA-III算法是由Deb[18]等人在NSGA-Ⅱ算法基础上,基于参考点提出的第三代带有精英保留策略的快速非支配多目标优化算法,在相关领域中取得了较为广泛地应用[19,20]。该算法主要针对三维及以上维度目标,采用参考点的选择操作代替NSGA-II 算法中拥挤距离的选择操作来保持非支配解的多样性,从而解决了高维优化问题中非支配解个体数量呈指数增长和个体间优劣难区分的问题。模型中雨水排水管道和调蓄池设计的优化目标函数个数为3个,针对公式(1)~(3)所示的多目标优化问题,利用良好分布的参考点来保持种群的多样性,采用NSGA-III算法,对求解Pareto曲面。
建立基于SWMM 的城市排水管网模型,并通过动态链接库调用SWMM 模型计算结果作为NSGA-III 算法的函数评价。NSGA-III算法中的每一个体都代表优化问题的潜在解,城市雨水排水系统多目标优化流程如图1所示,其中关键的步骤如下:
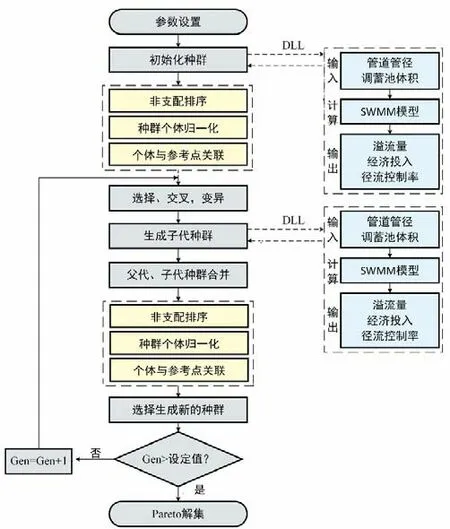
图1 城市排水系统多目标优化算法流程Fig.1 Flow chart of multi-objective optimization algorithm for urban drainage system
(1)种群初始化:初始化算法参数,根据管径与调蓄池体积范围随机生成大小为N的初代种群;
(2)种群非支配排序:种群中的个体根据相互间的支配关系分为若干层级,对所有个体进行归一化并关联至参考点;
(3)通过遗传算子进行遗传:对种群执行选择、交叉和变异,生成子代种群;
(4)种群合并:对父代和子代进行合并构成大小为2N 的种群,进行非支配排序、归一化并关联至参考点;
(5)精英保留策略:根据排序结果从合并的种群中选择大小为N的新子代种群;
(6)判断算法终止条件:算法最大迭代代数达到Gen则终止迭代,输出最优Pareto解。
3 案例应用分析
3.1 研究区概况
案例区域位于陕西省西安市南郊,区域面积为5.52 km2。该区域属于温带半湿润大陆性季风气候,降水多集中于5-10月份,且多以短历时强降雨的形式出现。根据西安市城市排水防涝综合规划,该区域内涝防治标准为50 a 一遇,然而,由于老旧城区下垫面不透水率较高,地下管线设计标准较低,部分路段面临着逢雨必涝的问题。因此,通过最大化优化原有排水管网与调蓄池等灰色设施,提高城市内涝防治标准显得尤为重要。案例区域位置见图2。
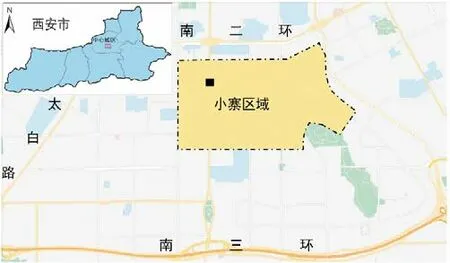
图2 研究区域位置示意图Fig.2 Location diagram of study area
3.2 SWMM模型构建
3.2.1 模型概化
利用研究区排水管网、下垫面与地形等资料,基于SWMM模型对排水系统进行概化。小寨区域SWMM 模型包含子汇水区61 个,蓄水池3 个,雨水管道79 条,其中主管道29 条(管径不小于1.5 m),片区雨水排口1 个。研究区综合不透水率为0.65,雨水经南北向主管道汇流至北边界,并由西北角排口排出。研究区SWMM模型概化见图3。
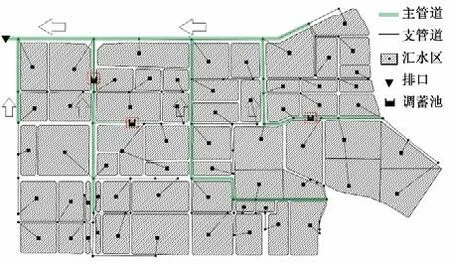
图3 研究区SWMM模型概化Fig.3 Generalization model of study area SWMM
3.2.2 率定与验证
SWMM 模型参数主要涉及洼蓄、下渗以及地表与管网糙率等相关参数。参考气候和地质条件相同的临近区域[21]进行取值,见表1。
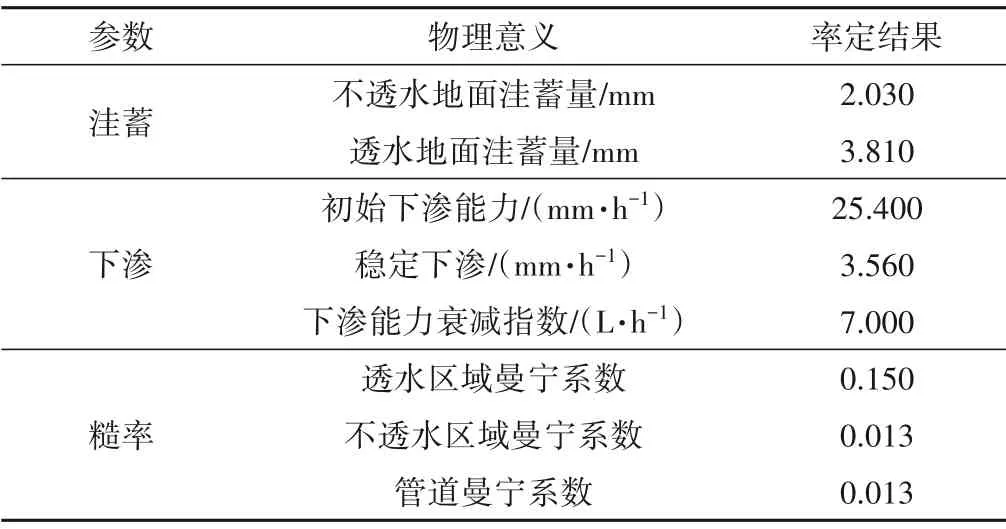
表1 SWMM模型参数率定结果Tab.1 Calibration results of SWMM model parameters
选取2019年8月3日降雨,通过下游排口流量监测资料对模型进行验证,下游排口实测与模拟流量过程结果见图4。从图4中可以看出,排口的流量模拟值和实测值结果基本吻合,二者的峰值滞后于降雨峰值,符合城市产汇流基本规律。采用Nash-Sutcliffe(NSE)系数进行模型精度评价,实测值与模拟值之间的纳什效率系数NSE=0.71,大于0.5,说明模型参数的设置较为准确。
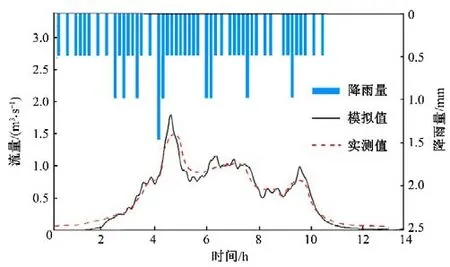
图4 2019年8月3日场次降雨及排口流量实测与模拟过程线Fig.4 Measured and simulated hydrograph of rainfall and discharge on August 3,2019
3.2.3 设计降雨工况
根据当地暴雨强度公式,以50 a一遇短历时(120 min)芝加哥雨型设计降雨情景为例,对研究区的雨水排水系统进行优化,并对10 a一遇、20 a一遇和50 a一遇不同设计降雨下的排水管网节点总溢流量进行比较。设计降雨过程见图5,10 a 一遇、20 a一遇和50 a一遇降雨总量分别为50、61、76 mm。

图5 设计暴雨过程线Fig.5 Design storm hydrograph
3.3 优化结果分析
结合已验证的SWMM 模型,通过NSGA-III 优化算法构建研究区域雨水排水系统多目标优化模型。选取了29 条主管道与3 个蓄水池作为优化的决策变量,根据当地排水防涝规划和设计标准,式(5)中管径可选范围E为1.5~4 m。考虑到管网优化设计模型的复杂度及计算成本,在粒子群优化过程中生成100 个粒子的初始种群,每个粒子都是优化问题的候选解决方案,种群以150次迭代在搜索空间中移动,以寻找最优解。
在前述设置的多目标优化模型的基础上,以50 a 一遇设计降雨为例,对研究区域的管网和调蓄池进行优化设计,在预设的种群规模和迭代次数下得到最优的Pareto 解集,并根据区域实际情况综合评价优化结果。图6 给出了NSGA-III 优化算法在迭代150次的Pareto解集。
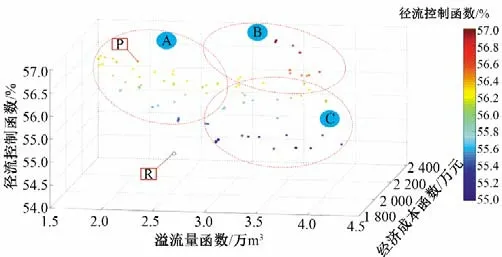
图6 优化收敛曲面Fig.6 Optimization convergence surface
由图6 可知,在经过迭代求解之后,得到的解的个数为100个,相比对原始方案,3 个目标函数都收敛到了相对较小的范围,说明优化提升效果较为明显;其中溢流量函数的解区间为1.5~4.2万m3,经济成本函数的解区间为1 900~2 400 万元,径流控制函数的解区间55.6%~56.4%,相比于优化前的方案(R 点)有较为明显的提升,尤其是径流控制函数目标,优化结果均优于原设计方案。根据解集的分布情况可分为A、B 和C 3 个区域,其中A 区域在整个解集中处于靠近经济成本轴,远离溢流量轴,且位于径流控制轴中段,即组A 的解溢流量较小、经济成本较高、径流控制效果适中,适用于溢流量要求较高的设计方案;组B 中的解相比于组A 和组C,距离经济成本轴和溢流量轴均较远,但位于径流控制轴最高的位置,即组B的解溢流量和经济成本相对较高,径流控制效果良好;组C 的解靠近溢流量轴,远离经济成本轴,且处在径流控制轴偏下段,其解溢流量和径流控制效果较差,经济成本较低,适用于经济成本投有限、排水防涝标准要求低的地区。
将优化收敛解投影到溢流量函数-经济成本函数平面上,如图7 所示。鉴于案例区域人口与资源聚集,积水致灾损失较高,优先考虑从A 区域选取优化结果,以溢流量和经济成本均较低,且径流控制率较高的P点作为最终优化结果,并与原始方案(R 点)进行对比,如表2 所示。50 a 一遇设计降雨条件下,溢流量、经济成本与径流控制3个目标均得到了改进:溢流量下降了11.7%;经济成本下降了4.55%;径流控制提升了4.06%。经过优化的雨水排水系统可在有限经济成本内,有效缓解城市积水灾害,更大限度实现雨水回用,优化效果显著。P点对应的优化方案中雨水管道优化前、后管径见表3。优化前3 个调蓄池容积分别为2.70、1.89、2.60 万m3,优化后3 个调蓄池容积分别为3.58、1.94、1.67 万m3。
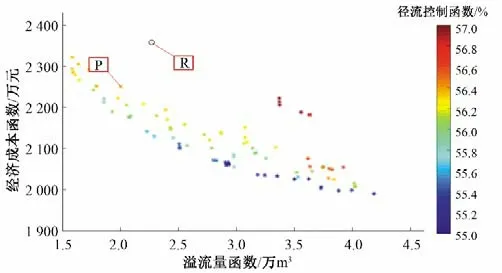
图7 经济成本函数-溢流量函数对比Fig.7 Comparison of economic cost function and overflow function
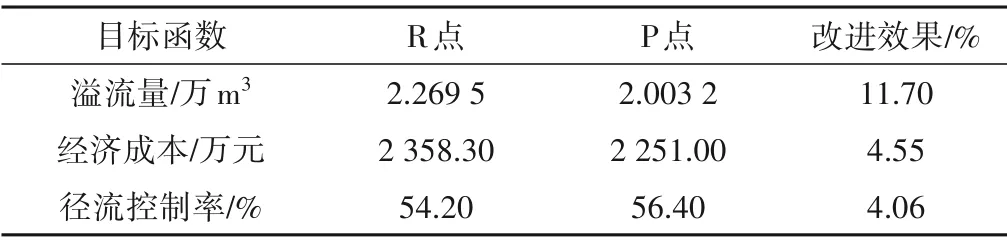
表2 50 a一遇降雨优化前、后效果对比Tab.2 Comparison of lifting effect before and after 50 a optimization
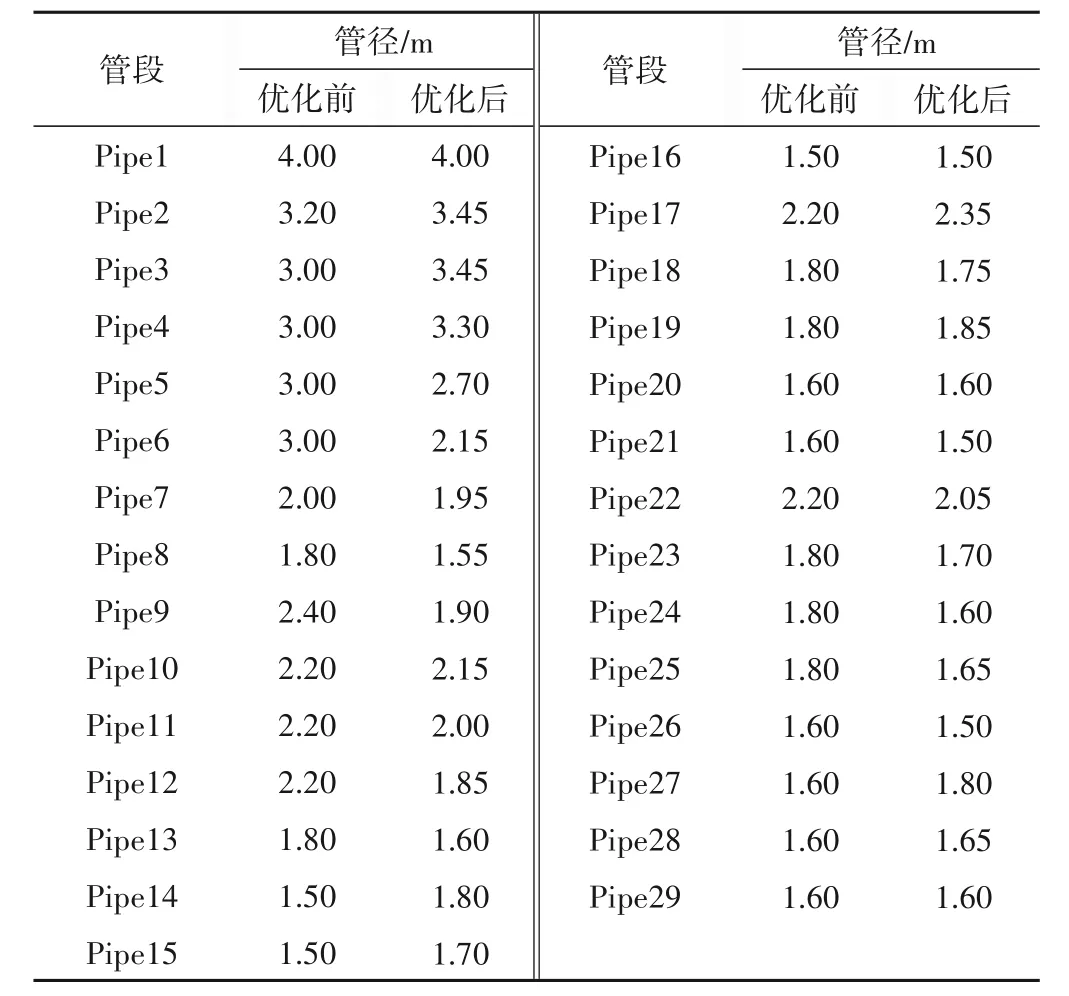
表3 雨水主管优化前、后对比管径Tab.3 The diameter of the main pipe network before and after optimization
为评估排水管网系统优化效果,以10 a 一遇、20 a 一遇和50 a一遇设计降雨为例,对不同设计方法的最优结果进行评估,见表4。与原规划方案相比,优化方案在不同重现期降雨条件下均得到了改进,且50 a 一遇设计降雨下的优化效果最为显著。随着降雨重现期的增大,城市雨水排水系统优化效果越来越明显。
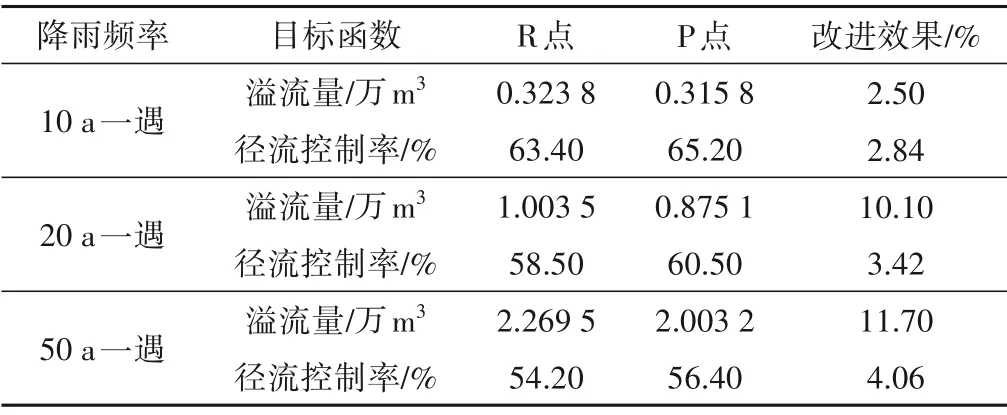
表4 各重现期优化前后提升效果对比Tab.4 Comparison of improvement effects before and after optimization of each return period
4 结 论
通过SWMM 模型计算排水分区降雨径流过程,并结合NSGA-III 算法,提出一种城市灰色排水设施优化设计方法。该方法以管网节点溢流量、经济投入和径流控制率为目标,以水力特性为约束条件,求解排水管网和调蓄池的最优设计方案。
以西安市小寨区域为例,选取50 a 一遇设计降雨对排水系统进行优化,并对三场不同重现期设计降雨的优化效果进行比较,结果表明,优化方法在三个目标上均优于依靠设计人员经验的传统方法,可有效解决城市雨水排水系统排水管网与蓄水池的最优组合问题。通过优化排水管网可使管道布设更加合理化,在付出较小的经济成本下可有效减轻城市洪涝;而合理布设调蓄池可减轻灰色排水系统总负荷,增大径流控制率。该方法可为灰色排水设施的设计提供指导。

