高填方场地水池结构振动台试验设计与数值分析

陈 增，周立业，赵国强，陈锦剑，3

（1.上海交通大学土木工程系，上海 200240；2.上海城建市政工程（集团）有限公司，上海 200032；3.上海市公共建筑和基础设施数字化运维重点实验室，上海 200240）

0 引 言

随着西部大开发战略和城镇化建设的逐渐深入，建设用地不断增加，大量的高填方场地工程涌现出来。同时，工业用水与居民生活用水的需求量也日益增长，水厂建设工程应运而生。而西南地区处于地震带周围，中小型地震时常发生，研究特殊填方地基上水池结构的抗震安全问题十分必要。

近年来，许多学者主要采用室内缩尺模型试验和数值模拟的方法探究土与结构体系相互作用的规律［1，2］。振动台试验研究最早可追溯到20 世纪70年代，Kubo［3］首次进行了桩—土—结构动力相互作用的振动台试验；近年来，国内外学者做了大量的试验研究工作，Haeri等［4］利用设置侧向玻璃窗口的刚性模型箱开展了液化场地中上部结构与群桩基础动力反应的振动台试验；高小波等［5］采用振动台试验研究了不同地震波作用下储液罐的晃动波高、储罐提离等动力响应问题，研究成果可为储罐设计提供参考；景立平等［6］以核岛厂房—桩基—土体整体结构体系为研究对象，开展了大型振动台试验，确定了桩基及上部结构的薄弱位置。

数值分析也是研究地基—上部结构动力响应问题的重要方法［7，8］，较于振动台试验，其在复杂工况及参数分析方面具有优势。刘洁平等［9］采用势流体理论，建立钢筋混凝土水池的液固耦合分析模型，分析了不同参数对水池抗震性能的影响；花立春［10］运用ADINA 有限元分析软件，针对某钢筋混凝土水塔在地震作用下的流固耦合动力响应进行了计算分析，确定了水塔结构的薄弱部位及加固措施；于磊等［11］针对核电结构的抗震性能及土体与结构动力反应规律进行了二维数值模拟研究，分析了输入地震波周期、上部结构质量和刚度对桩基的受力和变形特征影响；Badry 等［12］以尼泊尔地震为背景，综合考虑了桩土接触、半无限地基边界条件，对不同形式非对称高层建筑的结构体系进行动力分析。

综上所述，国内外学者在土与结构动力相互作用领域已取得不少研究成果，但针对震区填方地层上部水池结构的抗震问题研究较少。本文根据西南地区某水厂建设工程的特点，设计了振动台缩尺模型试验。针对拟开展的试验，建立三维数值模型以验证试验设计的合理性，主要分析了多种工况下水池结构、地基土层的动力响应规律。

1 高填方场地振动台试验设计

1.1 工程概况

拟建水厂项目工程位于四川省自贡市，抗震设防烈度为7度。场地地貌单元整体属于丘陵地貌，模型地基根据地质勘察报告进行合理简化，确定研究场地综合池2 下部的地基条件为挖填方结合场地，填方段从上至下依次为：人工填土（9 m）、种植土（1.8 m）、软塑粉质黏土（5.2 m）、中等风化砂岩（5.7 m）、中等风化泥岩（8.3 m）等。拟研究综合池的尺寸为：77.8 m×60.8 m×13.5 m，水池结构埋深3.5 m。进行室内缩尺试验时，考虑试验材料制作的简易性与可操作性，对性质相近的土层进行合并，取上部填土层16 m，下部基岩层14m，土层总厚30 m。

1.2 相似比确定

相似比设计时，需要考虑振动台的台面尺寸、试验能力及模型地基等客观情况，根据Bukingham-π 定理，选取模型几何尺寸、密度、加速度为基本物理量，即模型体系加速度相似系数为1，密度相似常数为1，模型几何相似常数为1/100 进行试验，在线弹性范围内对其他相似关系进行推导。试验的主要相似指标包括力F，应力σ，应变ε，输入振动时间T，黏聚力c，内摩擦角φ等，现选取部分指标进行推导如式（1）～（3），其余参数相似关系如表1所示。

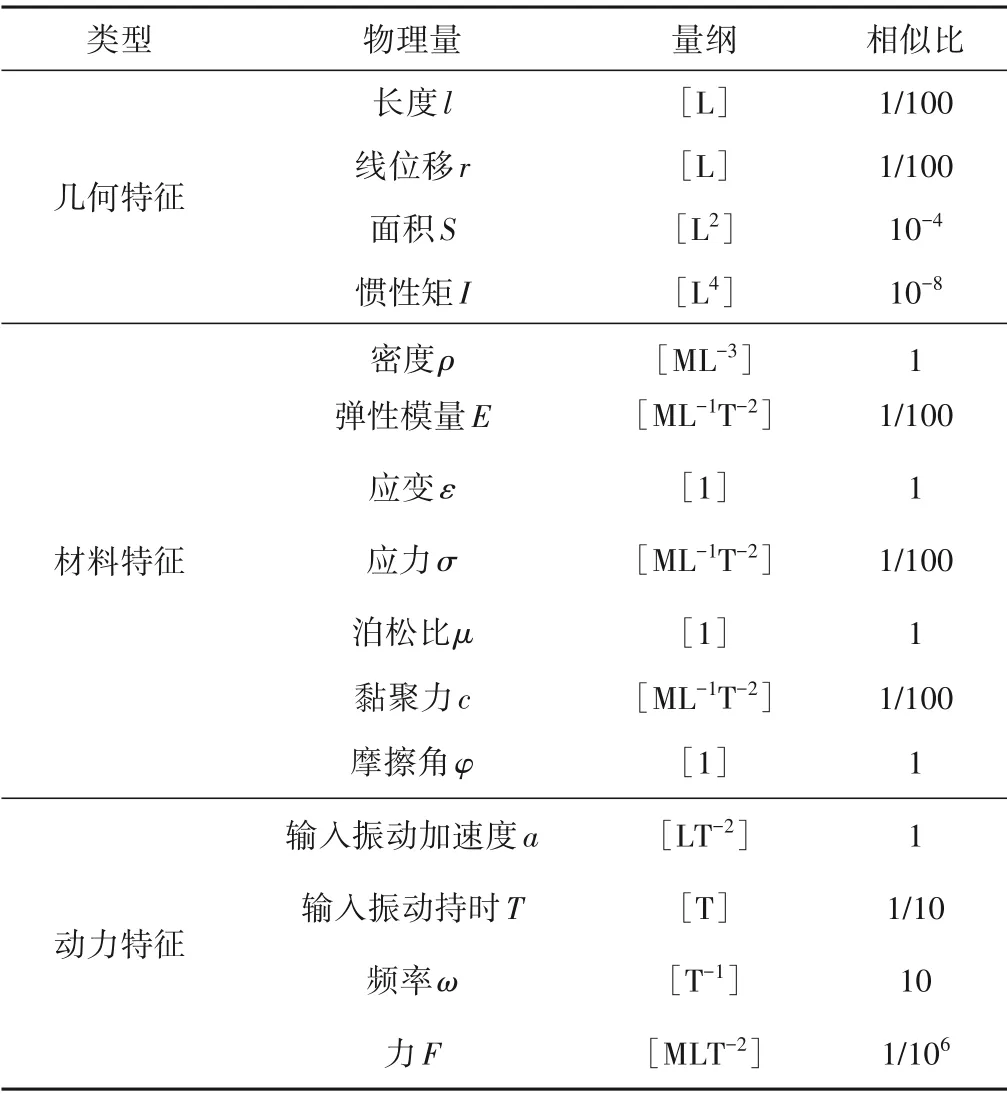
表1 振动台试验模型相似关系Tab.1 The similarity relationship of shaking table test model

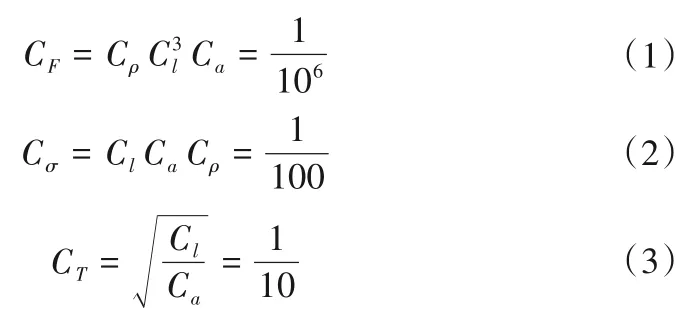
1.3 传感器布设

分别于水池结构上方两处典型位置布设激光位移传感器（J1、J2）监测结构不同位置处的位移变化，并在地基处选取6 处典型位置布设加速度传感器（A1～A6）监测土层及上部结构的加速度动力响应。缩尺试验整体模型及传感器布设如图1所示。

图1 振动台整体模型及传感器布设Fig.1 The overall model of the shaking table and sensor layout

1.4 试验工况设计

本次试验选取汶川卧龙台地震波强震段作为输入地震动（时间相似比为1/10，输入地震波为16 s），汶川卧龙波的加速度时程与对应傅里叶谱如图2 所示。在输入地震动前、后均输入白噪声以得到整体结构体系的固有频率和阻尼比等动力特性。考虑到施加地震动后结构体系的损伤具有不可逆性，在试验中将汶川卧龙波逐级增大输入，具体加载工况如表2所示。

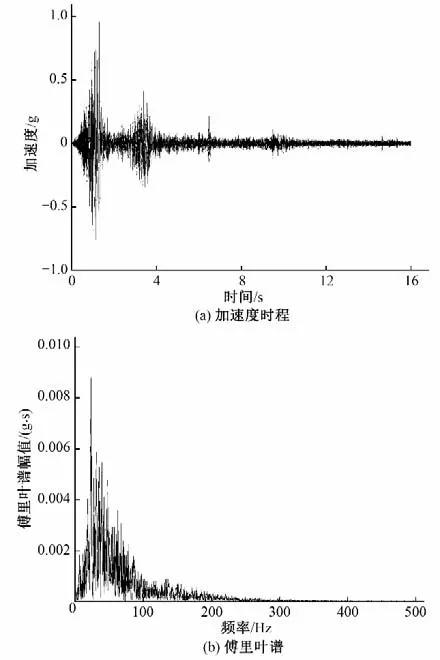
图2 汶川卧龙波加速度时程及傅氏谱Fig.2 Acceleration time history and Fourier spectrum of Wenchuan Wolong wave

表2 试验加载工况Tab.2 The load events in the test

2 振动台试验数值建模

采用Abaqus 有限元软件建立与振动台缩尺模型试验相一致的三维计算模型，数值分析基于隐式动力分析方法。整体有限元模型和典型监测点位置如图3 所示，监测点分别位于水池结构中部两侧各0.1 m 土体底面、分界面及顶面位置。土体、上部结构均采用实体单元（C3D8）模拟，土体本构采用莫尔库伦弹塑性模型，水池结构采用弹性模型，材料参数如表3所示。为保证地震波传播时的精度，划分网格时控制尺寸在最高频率对应波长的1/8～1/10。

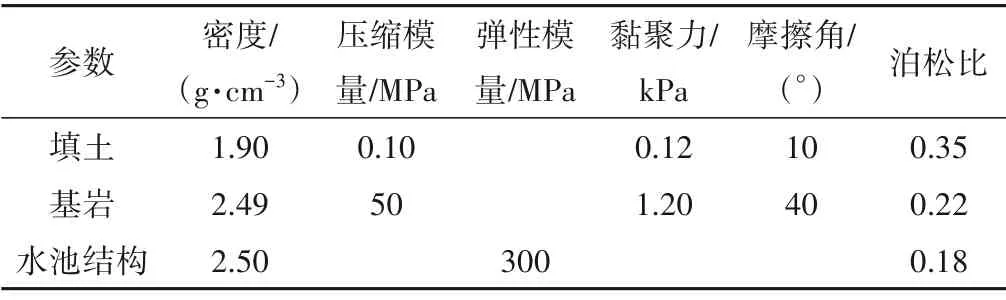
表3 材料基本参数（根据相似比缩尺参数）Tab.3 The basic parameters of the material（based on the similarity ratio scaled parameters）

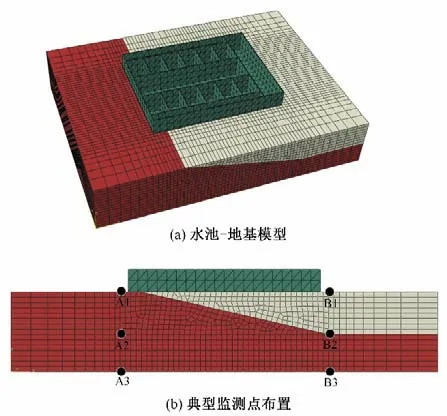
图3 土体及结构数值计算模型Fig.3 Soil and structure numerical calculation model

2.1 边界条件设置

为研究半无限地基地下结构的动力响应，采用黏弹性人工边界，通过在截断边界上布设弹簧和阻尼器系统，吸收边界上的散射波能量，模拟远域地基的弹性恢复能力。同时，根据已有研究［13］，模型底部采用等效节点力的数值计算结果与理论解一致，采用此种方法在模型底部施加地震动。

2.2 阻尼设置

在研究岩土动力问题时，土体的阻尼起到能量耗散作用，不可忽视。根据瑞利阻尼理论确定材料的阻尼参数，如式（4）所示。其中，土体和结构物的自振频率可通过Frequency 分析步求得。

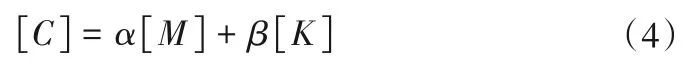
式中：α为质量阻尼系数；β为刚度阻尼系数，见计算式（5）；ω1、ω2分别为第一、二阶自振频率；ξ为阻尼比，取5%。

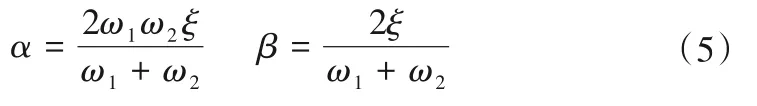
2.3 动水压力设置

本次研究对象为水池结构，为考虑地震荷载作用下动水压力对结构变形及力学响应的影响，根据《水运工程抗震设计规范（JTS146-2012）》［14］，采用附加质量法进行计算，动水压力的公式如式（6）。同时，参考已有研究成果［15］，Westergaard 附加质量公式分析实际问题时偏于安全保守，采用折减系数0.8 进行适当修正，计算结果与实际震害效果更为吻合，故本文采用式（6）计算时，对其进行折减修正。

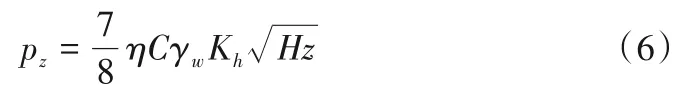
式中：pz为水深z 处的地震动水压力，Pa；η为折减系数；C为综合影响系数；γw为水重度，N/m3；Kh为水平向地震系数；H为水池深度，m；z为计算点至水面距离，m。

3 结果分析与讨论

数值计算以振动台试验设计工况为基础，分别考虑不同地震动强度及上部结构不同储水量等条件进行计算分析。基本模型以0.5 g汶川卧龙台地震波作用于基岩底面，上部水池结构满载工况为例，同时，为了提高计算效率，计算模型输入地震波选用前4 s波形密集段。

3.1 地基土体动力响应分析

拟建结构所处场地为高填方边坡土层，土体性质差异大，不同位置地层的动力响应区别显著。图4（a）、（b）所示为监测点A1、A2、A3，B1、B2、B3 的加速度响应时程曲线。观察可知，地震波在硬质岩层由下至上的传播过程中，加速度峰值不断增加，地表加速度峰值为输入地震波峰值的1.488 倍，而地震波形与输入波形一致性较好；而在上软下硬地层中，地震波幅值呈现先增后减的趋势，在填方软土地层中，由于阻尼作用更大，地震波的高频部分被土体过滤，显示为地表的加速度时程曲线较底面输入地震波的幅值与能量均产生衰减，呈现明显的低频特性，地表加速度峰值仅为底面位置加速度的0.751。

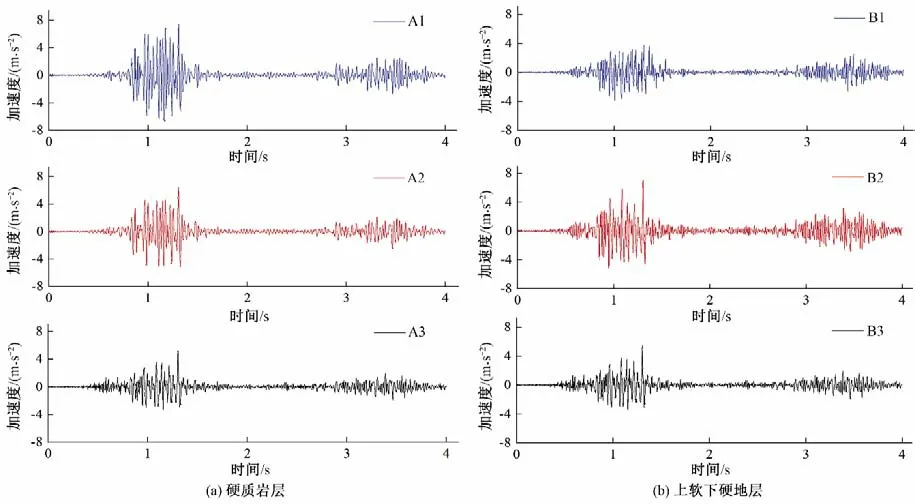
图4 地基不同位置加速度响应Fig.4 Acceleration response of foundation at different positions

考虑不同地震动强度对地基土层动力响应的影响，分别调整地基底面输入地震波峰值为0.1、0.3、0.5 g。加速度放大系数定义为监测点处加速度峰值amax与基岩处输入地震动加速度峰值a′max之比。观察图5 可知，在不同强度地震动作用下，硬质岩层的加速度放大系数随高程逐渐增大，上软下硬土层的加速度放大系数则在土层分界面处出现拐点，整体表现为先增后减的趋势。随着输入地震动强度的增大，土体非线性特性逐渐明显，阻尼也随之改变，较低强度地震动作用下，土体可能仍处于弹性阶段，土体的加速度放大系数更大，在大震激励下，土体表现出非线性特性，加速度放大系数反而减小。

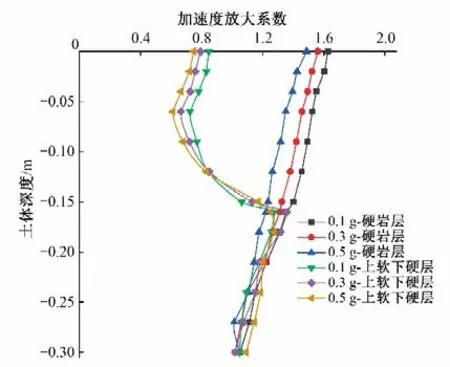
图5 地基土体加速度放大系数Fig.5 Acceleration amplification coefficient of foundation soil

3.2 水池结构位移分析

高填方场地工程中，由于原状岩体与填筑土体的压缩性差异，在地震荷载作用下常发生因地基差异沉降导致的上部结构产生过大位移而破坏。

水池结构在正常运营期间，池内水位会发生改变，选取3种典型工况，即池内空载、半载、满载进行分析研究。选取水池底板中部为监测位置，绘制不同工况下地震动输入结束后结构底板的残留位移曲线。由图6可知，随储水量的增加，结构最大竖向位移呈现非线性增长。随着储水量的改变，水池结构自振频率也随之改变，当水体质量增加时，结构自振频率减小，即随着动水压力的增大，结构刚度减小，在地震动荷载作用下的动力响应愈加显著。由于上部结构的整体刚度大，水池结构近似发生绕岩体位置处一固定点旋转的倾斜模式。

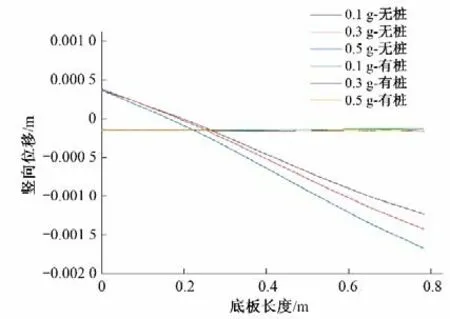
图6 不同储水量结构竖向位移Fig.6 Vertical displacement of structures with different water storage

地震动强度对水池结构的竖向位移也有显著影响，满载工况不同强度地震动作用下水池结构竖向位移最大值如表4 所示，位移最值随地震动强度的增大呈现非线性增长。

表4 不同地震动强度水池结构竖向位移 mmTab.4 Vertical displacement of pool structure with different ground motion intensity

3.3 水池结构受力分析

水池结构在地震荷载作用下的应力响应也是抗震分析的重要内容之一。在水平向地震荷载作用下，挖填方交界位置附近的水池中部墙体所受拉应力最大，不同工况下应力集中部位的最值如表5 所示。随着地震动强度及水池储水量的增加，最大主应力非线性增大，特别是在满载工况下，较大地震动强度使水池结构局部墙体最大主应力超过抗拉强度标准值（应力相似比为1/100）。通过分析水池结构的应力集中部位，可更好确定其受力薄弱位置，以采取相应加固措施。

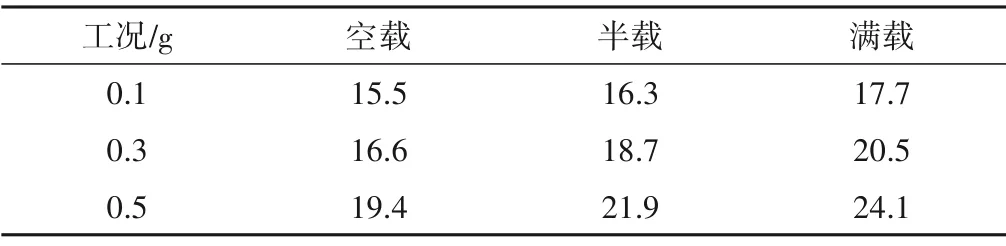
表5 不同工况水池结构最大拉应力应力响应 kPaTab.5 The maximum tensile stress of pool structure under different conditions

3.4 地基处理措施

为保证高填方场地上部水厂结构的安全稳定，通常可采用的地基处理方式包括：增设桩基、换填垫层、强夯处理等［16］。本文针对前两种方法进行建模分析，探究不同地基处理方式对控制水池结构竖向位移的影响。

（1）增设桩基。图7为水池结构—桩基三维模型图，群桩基础由15×12 共180 根基桩组成，桩体采用C3D8 实体单元进行模拟，按几何相似比1∶100 取桩径0.01 m，桩长根据岩层坡度分别取为0.1、0.14、0.18 m，桩端进入岩层累计长度为0.05 m。桩顶与结构底板采用绑定连接，桩土间设置通用接触，法向为硬接触，切向为摩擦接触，其他参数如表6所示。不同工况下填方区水池结构底板的位移最值如表7 所示，观察可知，增设桩基后，可以有效控制填方地基区域上部结构的竖向位移，即使在满载情况下，水池结构的位移也得到有效控制。

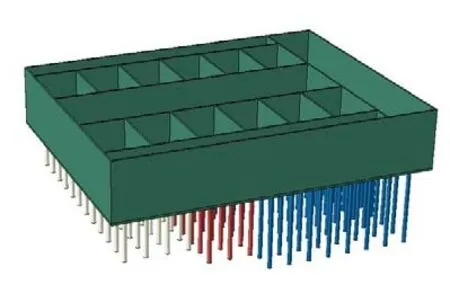
图7 水池-桩基模型Fig.7 Pool-pile foundation model

表6 桩体模型材料参数（根据相似比缩尺参数）Tab.6 The parameters of pile model（based on the similarity ratio scaled parameters）

表7 有、无桩基水池结构竖向位移对比 mmTab.7 Comparison of vertical displacement of pool structure with and without pile foundation

（2）换填土层。回填区填方土体的刚度也是影响上部结构及地基土体受力及变形特征的重要因素，地基刚度调整应结合现场实际工况，选择合适的填土材料、填筑工艺和合理的基础形式设计，以达到提高建筑整体刚度、减小差异沉降的效果。分别调整填方区土体压缩模量为0.2～0.4 MPa进行分析（根据相似比缩尺参数），表8所示为不同土体压缩模量下水池结构底板竖向位移最值，当填土压缩模量增大后，结构竖向位移明显减小，即改良填方地基的性质可在一定程度上控制填方地基不均匀沉降。

表8 不同土体压缩模量水池结构竖向位移对比 mmTab.8 Comparison of vertical displacement of pool structure with different soil compression modulus

4 结 论

针对震区高填方场地上部水池结构与地基土体的动力响应问题进行研究，根据实际工程特点，设计了振动台缩尺模型试验，并采用数值分析的方法对振动台试验方案的合理性进行验证分析。主要得到以下结论：

（1）基于振动台缩尺模型的数值计算结果表明，初步试验设计方案具有可行性和合理性，同时，研究结果可进一步为试验方案优化及传感器、应变片等布置提供参考。

（2）地震波由基岩处向上传播的过程中，在硬质岩层中，加速度峰值逐渐增大，波形与输入波基本一致；在软弱填土层，由于较强的滤波作用，加速度峰值逐渐降低，靠近地表的时程曲线幅值和能量均发生衰减。

（3）水池结构的竖向位移随地震动强度、储水量的增加非线性增大；地层挖填方交界位置附近水池中部墙体所受拉应力最大，为受力薄弱部位，在设计中应加以关注；增设桩基及改善填方土体性质均可有效控制水池结构的位移与倾斜。