半直线上双极等熵可压缩Navier-Stokes-Poisson 方程组的稳态解

王 雷 李 丽 黄紫光

（1.吉林财经大学，吉林 长春 130000； 2.吉林省医药中等职业学校，吉林 长春 130000）

在半导体物理中，双极等熵可压缩Navier-Stokes-Poisson（以下简称NSP）方程组有着十分重要的应用，它可以用来描述电子和空穴的输运现象[1]。本文讨论定义在半直线上的双极等熵定常的NSP 系统：

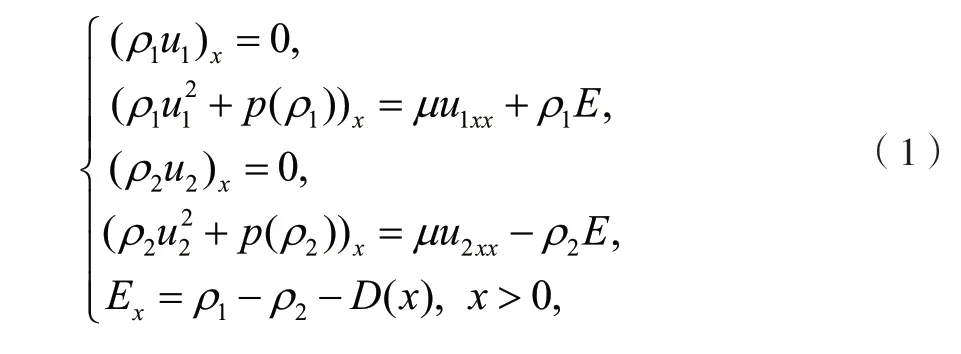
附带边界条件：

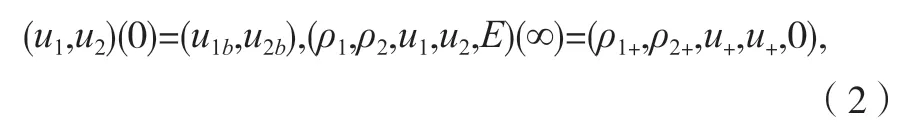
并且假设：

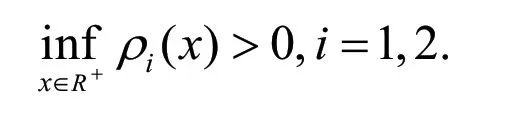
这里电子密度ρ1、空穴密度ρ2、电子速度u1、空穴速度u2和电场E为未知函数，而p(.)代表压力函数，服从γ律，即具体表达式为：

p(ρ)=Kργ,K＞0,γ≥1.

此外，粘性系数μ＞0，全部边界数据均为常值。背景掺杂函数D(x)=ρ1+-ρ2+，它可以不为零。

半直线上可压缩NSP 方程组的研究已经取得了一些进展，Hong H 等[2]和Wang L 等[3]讨论了单极等熵情形的外流问题和内流问题，Duan R-J 等[4]研究了双极等熵NSP 系统强解的整体存在性。Zhou F 等[5]给出了该强解对稳态解的时间衰减速率。值得指出的是：上述双极结果都是关于零掺杂情形的，其稳态解本质上是定常的可压缩Navier-Stokes（简称NS）系统的解与零电场共同构成的向量，因此无法反映重要的半导体电场效应。

1 主要结果

鉴于物理上半导体掺杂性质的重要性，本文讨论非零常值掺杂情形下定常问题（1）-（2）的可解性。此时，定常的可压缩NSP 方程组的数学结构变得更加复杂，以至于不能效仿零掺杂情形的处理方式来求解。从而不得不另寻他法：首先将其转化成五阶的自治常微分系统，接着应用稳定流形定理，提出定常问题（1）-（2）解的存在性判据，同时给出空间衰减率。为此，我们需要按照下面步骤重构原始问题。

1.在无穷区间[x,+∞)上积分质量方程并且使用边界条件推导出：

3.经过简单计算，我们推导出与定常NSP 方程组等价的自治常微分系统：

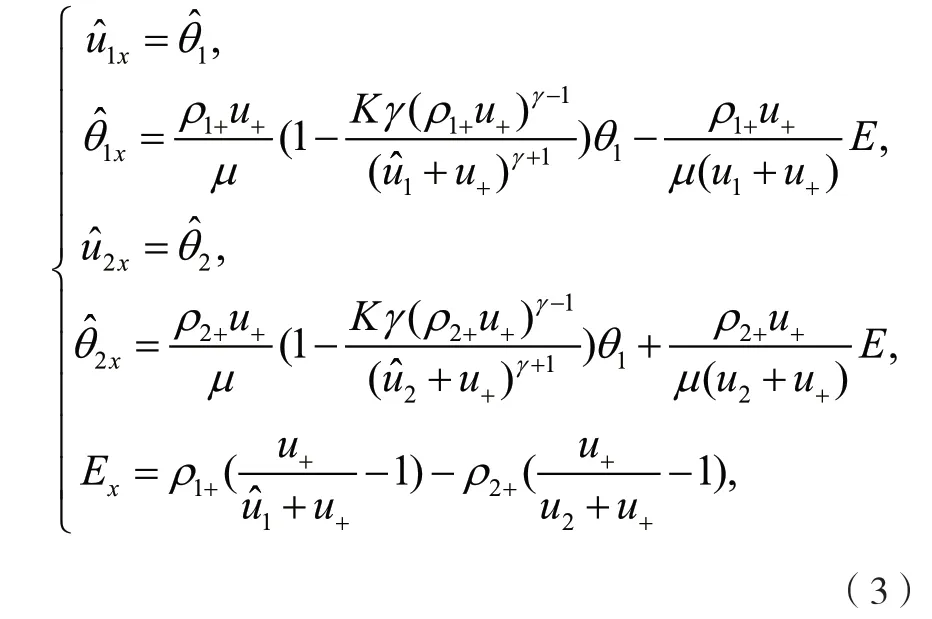
为了使解具有衰减性质，我们先验地假设：

注1：对于双极定常外流问题即u1b,u2b＜0，在无穷远渐近态处，当电子和空穴均为非超音速流或非亚音速流并且δ足够小时，定常问题（1）-（2）的解存在唯一。但是，当它们一个为超音速流另一个为亚音速流时，该问题是否存在解仍是一个研究课题。

注2：对于双极定常内流问题即u1b,u2b＞0，在无穷远渐近态处，当电子和空穴均为亚音速流或者一个为亚音速流而另一个为音速流并且δ足够小时，定常问题（1）-（2）的解存在唯一。但是，当它们皆为超音速流或者一个是超音速流而另一个是非超音速流时，该问题是否存在解仍是一个研究课题。

注3：我们只考虑了电子和空穴同为内流或外流的情形。对于一个内流一个外流的情形，目前不清楚：半直线上定常的NSP 系统是否可解？判据如何？解的性质怎样？

注4：这里参数δ满足小性假设是技术性条件还是本质要求，有待深入研究。

注5：与零掺杂情形相比，我们的稳态解（也称为边界层）包含了非零电场，为数学物理中研究电场效应提供了可能性。

2 定理的证明过程

证明：先证(i)。设u+=u1b=u2b=0，将常值向量(ρ1+,ρ2+,0,0,0)带入到定常的可压缩NSP方程组以及边界条件中，容易验证：它是定常问题（1）-（2）的平凡解。

为原点处的雅克比矩阵，而非线性项的具体形式为如公式2。

显然，F是光滑的向量值函数，并且在原点处成立F(0)=0,DF(0)=0。

设矩阵I是与矩阵A同阶的单位阵，则矩阵A的特征方程为：

由零值性知，D(λ)=0 至少存在一个负根。

情形2：u+,u1b,u2b＜0,并且M1+＞1,M2+≥1 或M1+≥1,M2+＞1

由韦达定理知，代数方程D(λ)=0 的所有根之和为：

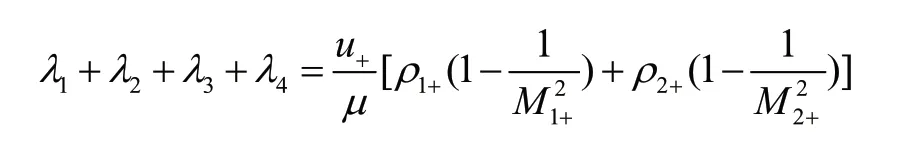
注意到u+＜0，故λ1+λ2+λ3+λ4＜0，于是，该方程必有一个具负实部根。

情形3：u+,u1b,u2b＜0,M1+=M2+=1

此时，直接求解方程：

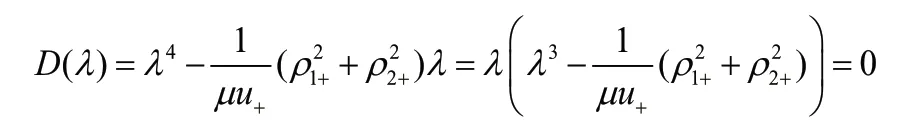
因为集合{(M1+,M2+)│M1+＜1,M2+≤1 或M1+≤1,M2+＜1 或M1+＞1,M2+≥1 或M1+≥1,M2+＞1 或M1+=M2+=1}与集合{(M1+,M2+)│(M1+-1)(M2+-1)≥0}相等，所以事实上我们已经在(ii)的假设下严格证明了：常微分方程组（3）的系数矩阵A至少存在一个具负实部的特征值。这里需要指出的是：技术上之所以能够得到如此结果，矩阵A本身的结构起到了关键作用。

最后，应用稳定流形定理到等价自治系统（3）-（5），立即得到：∃δ＜＜1，使得常微分系统（3）在原点处存在唯一局部稳定流形Ws。若则定常问题（1）-（2）存在唯一光滑解使得：

其中c＞0,λ＞0 至此，定理得证。