物联网环境下多设备载波通信干扰批量抑制方法
张 乐
(福建商学院 信息工程学院,福州 350506)
物联网(Internet of Things, IOT)环境下,为降低跳频信号遭受查验的概率,提升载波通信的安全性,在物联网环境下多设备载波通信中跳频信号的应用较为广泛[1-2]。在干扰信号持续增多的过程中,干扰方式也呈现多元化,导致载波跳频通信的抗干扰性能下降,不能满足现实所需[3]。其中一种主要的干扰方式是梳状阻塞干扰[4]。为提升信号传输性能与安全性,需对干扰实施批量抑制,其中重点研究方向为抑制梳状阻塞干扰[5]。
最小色散干扰抑制方法是通过运用信号的脉冲特性构建范数约束优化模型,将观测信号中的有价值信息提取出,并对最优权矢量实施运算,空域滤波观测信号后,实现基于最小色散算法的压制式干扰抑制[6];压缩感知信号重构干扰抑制方法是依据目标回波信号与干扰信号能量函数的特性差异,提取没有遭受干扰的目标回波信号数据,通过运用此数据同经过解线调处理的目标回波信号稀疏频域间的线性关联,建立压缩感知最小问题解算模型,实现对干扰信号的抑制[7]。以上2种抑制方法在信号去噪处理方面存在明显不足,无法提升整体抑制效果。小波去噪具备小波基选取灵活性与时-频局部化特征,可在叠加高斯白噪声的环境下将真实信号检测出来,不仅保留了信号的局部特征又可有效抑制噪声[8];独立分量分析(Independent Component Analysis, ICA)属于一种盲源分离技术,是通过运用优化算法在某个衡量保持独立的前提下,分解某组混合信号为数个单独成分,可有效分离多设备载波通信中的梳状阻塞干扰信号与跳频信号,具有较好的信号分离效果[9]。因此,本文通过有效结合小波去噪方法与独立分量分析算法,实现对通信混合信号的去噪处理与梳状阻塞干扰信号分离处理,达到批量抑制干扰信号的目的,为保障通信安全提供有效帮助。
1 通信干扰批量抑制方法
1.1 独立分量分析算法
独立分量分析算法的过程如图1所示。
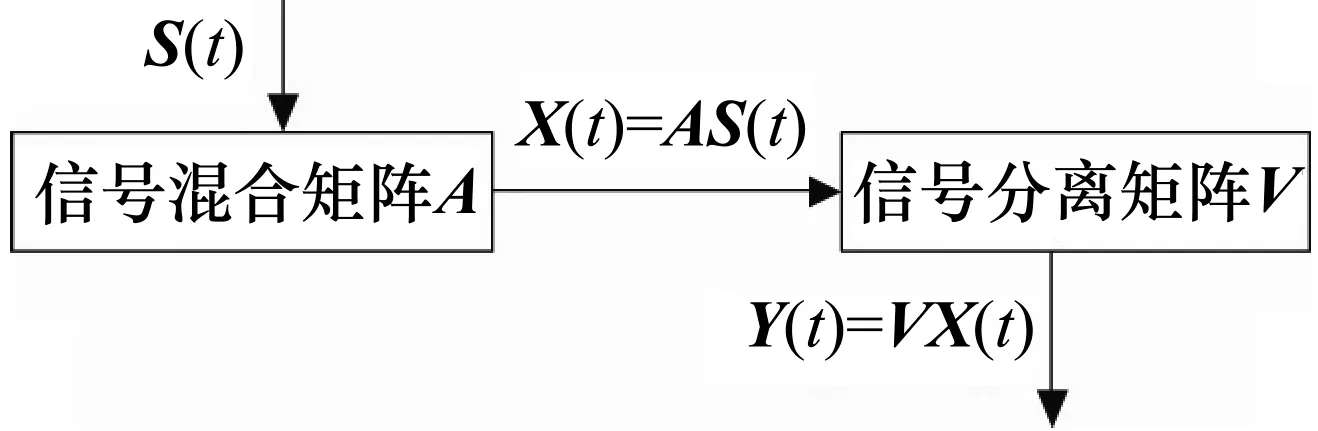
图1 独立分量分析算法过程
图1中,源数据所构成的N维矢量信号由S(t)表示,由信号混合矩阵A线性组合后形成混合信号X(t),也就是现实中所接收到的信号,其表达式为:
X(t)=AS(t)。
(1)
式中:混合矩阵A属于未知。混合信号X(t)经由信号分离矩阵V分解后,所获取到的估计信号Y(t)即为分离信号,可表示为:
Y(t)=VX(t)。
(2)
式中:分离矩阵V可通过独立分量算法求得。通过式(2)所得出的分离信号Y(t)属于源信号矢量S(t)或者源信号矢量某部分分量的可靠估计。现实中应用独立分量分析算法时,需具备的必要条件为:
1)源信号组S(t)中每个分量均需尽量达到统计独立性;
2)源信号组S(t)中各分量最高仅可具备1个高斯分布,且均值为0;
3)混合矩阵A属于1个列满秩矩阵,现实应用中尽可能地统一源信号组S(t)与混合信号X(t)的分量数目,也就是混合矩阵A为方阵,且存在逆矩阵A-1。
独立分量分析算法主要包含信号混合、信号分离及必要条件3部分[10],其目的是通过找寻1个分离矩阵V,分离混合信号后令分离信号保持互为独立的关系,并尽可能与源信号S(t)接近,实现最优信号分离效果。
1.2 基于独立分量分析的干扰批量抑制方法
基于独立分量分析的多设备载波通信干扰批量抑制方法整体过程如图2所示。
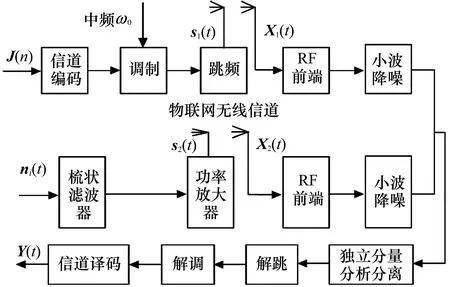
图2 载波通信干扰批量抑制方法过程
跳频信号s1(t)可经由信道编码、中频调制与跳频获取到,其序列用J(n)表示。运用功率放大器与梳状滤波器转换干扰信号为梳状阻塞干扰信号s2(t)。将2根天线设置于多设备载波通信的接收端,并以此作为独立分量分析算法实施分离的基础。那么现实中所接收到的信号即混合信号可表示为:
X(t)=US(t)+n(t)。
(3)
式中:s1(t)、s2(t)表示源信号;n1(t)、n2(t)表示噪声信号;X1(t)、X2(t)表示2根天线的接收信号。
1.2.1 小波去噪处理
在实施信号分离之前,需先对X(t)实施小波去噪处理[11],以提高干扰批量抑制的效果。
X(t)包含n(t)与S(t),即X(t)=n(t)+S(t)。先离散采样天线接收信号X(t)获取到M点离散信号X(m),其中:m=0,1,…,M-1,离散小波变换可表示为:
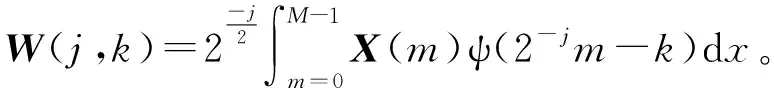
(4)
式中:W(j,k)为小波系数;ψ(x)为小波基;k为平移因子;j为缩放因子(小波分解层数)。
小波变换的递归实现方法可通过双尺度方程获取到,即为:
(5)
式中:与ψ(x)相对的低通滤波器与高通滤波器分别以l(·)和h(·)表示;Wh(j,k)为细节系数;Wl(j,k)为近似系数。相对的重构式可表示为:
(6)

通过双尺度三层小波分解X(m)的示意图如图3所示。
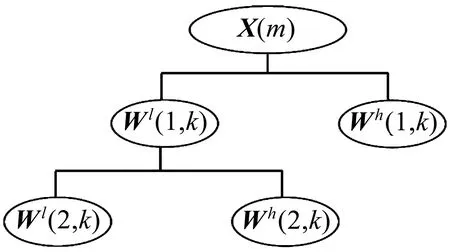
图3 双尺度三层小波分解X(m)
X(m)经三层小波变换分解之后,信号的能量大多在Wl(2,k)内聚集,噪声的能量大多在Wh(1,k)与Wh(2,k)内聚集,同时与噪声相比幅值所产生的小波系数更大。小波降噪是以阈值选择规则为依据设置一个门限值,运用硬阈值方法保留比此门限值高的小波系数,或采用软阈值方法根据某个固定量向零收缩,重构处理之后的小波系数,如此便能够将降噪之后的信号获取到[12]。
1.2.2 信号分离
X(t)经小波降噪之后,去除掉了噪声信号n(t),在X(t)中以独立源信号为前提时,需令输出信号保持相互独立方可实现混合信号的全部分离。经输出信号的高阶或二阶累计量矩阵群联合对角化程度表示独立分量分析的对照函数[13]。为完全分离源信号,应对如何将四阶累计量作为初始点通过结合四阶累计量矩阵群与对角化求得分离矩阵V,予以判别。
假设w是第N根天线的接收信号,E是权值矩阵,那么w=(w1w2…wN)T,w的四阶累计量矩阵第i行第j列元素可表示为:
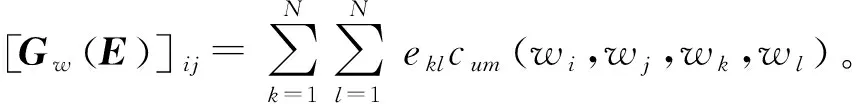
(7)
式中:i≥1,j≤N;ekl表示权值矩阵E的第k行第l列的元素;Gw(E)表示由向量w的所有四阶累计量所构成的累计量矩阵;cum(wi,wj,wk,wl)表示向量w内第i、j、k、l4个分量的四阶累计量。
白化之后的第N根天线观测向量w的表达式为:
w=W∪S=RS。
(8)
式中:W表示预处理矩阵;S内各个分量统计互为独立,向量w内各个分量相互间无关联。故矩阵R属于正交矩阵[14]。
设R的随机一列以ri(1≤i≤m)表示,且ri=(ri1ri2…rim)T,那么矩阵E可表示为:
E=riwN。
(9)
将式(8)与式(9)代入式(7),得到:
(10)
因各源信号之间互为独立关系,故当a=b=c=d时,cum(sa,sb,sc,sd)=k4(sa),则式(10)可简化为:
[Gw(E)]ij=mijk4(sk)。
(11)
式(11)可改写成:
Gw(E)=k4(sk)E。
(12)
由式(12)可知,Gw(E)属于对称矩阵,其特征分解形态可表示为:
(13)
那么Gw(E)还可表示成:
Gw(E)=VΛ(E)RT。
(14)
式中:Λ(E)表示特征值对角矩阵。
经由R二次型处理Gw(E)可得到对角矩阵Λ(E),以总体特征为依据将分离矩阵V求出[15]。
任选一组z个矩阵表示为E=(E1E2…Ez),求取随机某个Ez(1≤z≤Z)的Gw(Ez),同时求得矩阵R,尽可能地对角化处理完所有Gw(Ez)。为实现非对角化程度的各个度量Λ(Ez)=RTGw(Ez)R,所选取的度量指标应该是各Λ(Ez)内非对角元素的平方和,即:
(15)
预估得出分离矩阵V为:
V=RTW。
(16)
2 实验结果
以某市电力公司的物联网多设备载波通信系统作为实验对象,检验本文方法的实际抑制效果。运用Matlab编写仿真程序实施仿真实验,经由二进制数字频率调制方法(Frequency Shift Keying,2FSK)调制实验通信系统内的跳频信号,其中采样频率、信息速率及调速依次为380 kHz、1 480 b/s、1 480 hops/s。实验中所接收到的实验通信系统混合信号中包含噪声信号与源信号,如图4所示,其中源信号由跳频信号与梳状阻塞干扰信号组成。

(a)原始噪声信号幅值
2.1 去噪效果对比分析
选取最小色散干扰抑制方法(文献[6]方法)与压缩感知信号重构干扰抑制方法(文献[7]方法)作为本文方法的对比。分别运用3种方法对实验通信系统混合信号内的初始噪声信号实施去噪处理,获得去噪处理后的噪声信号幅值,如图5所示。
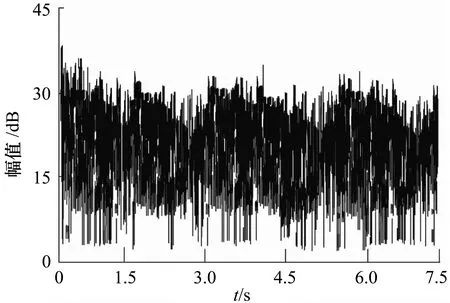
(a)文献[7]方法
由图5可知,与原始噪声信号幅值相比,3种方法均可实现不同程度的降噪处理,其中文献[7]方法的去噪效果较差,去噪后的噪声信号幅值依然较高;文献[6]方法的去噪效果居中,明显降低了原始噪声信号幅值;而本文方法的去噪效果最为理想,不但进一步地降低了原始噪声信号的幅值,而且去噪效果较为稳定。
2.2 信号分离效果呈现
通过本文方法对实验通信系统源信号实施信号分离,所获取到的分离结果如图6所示。
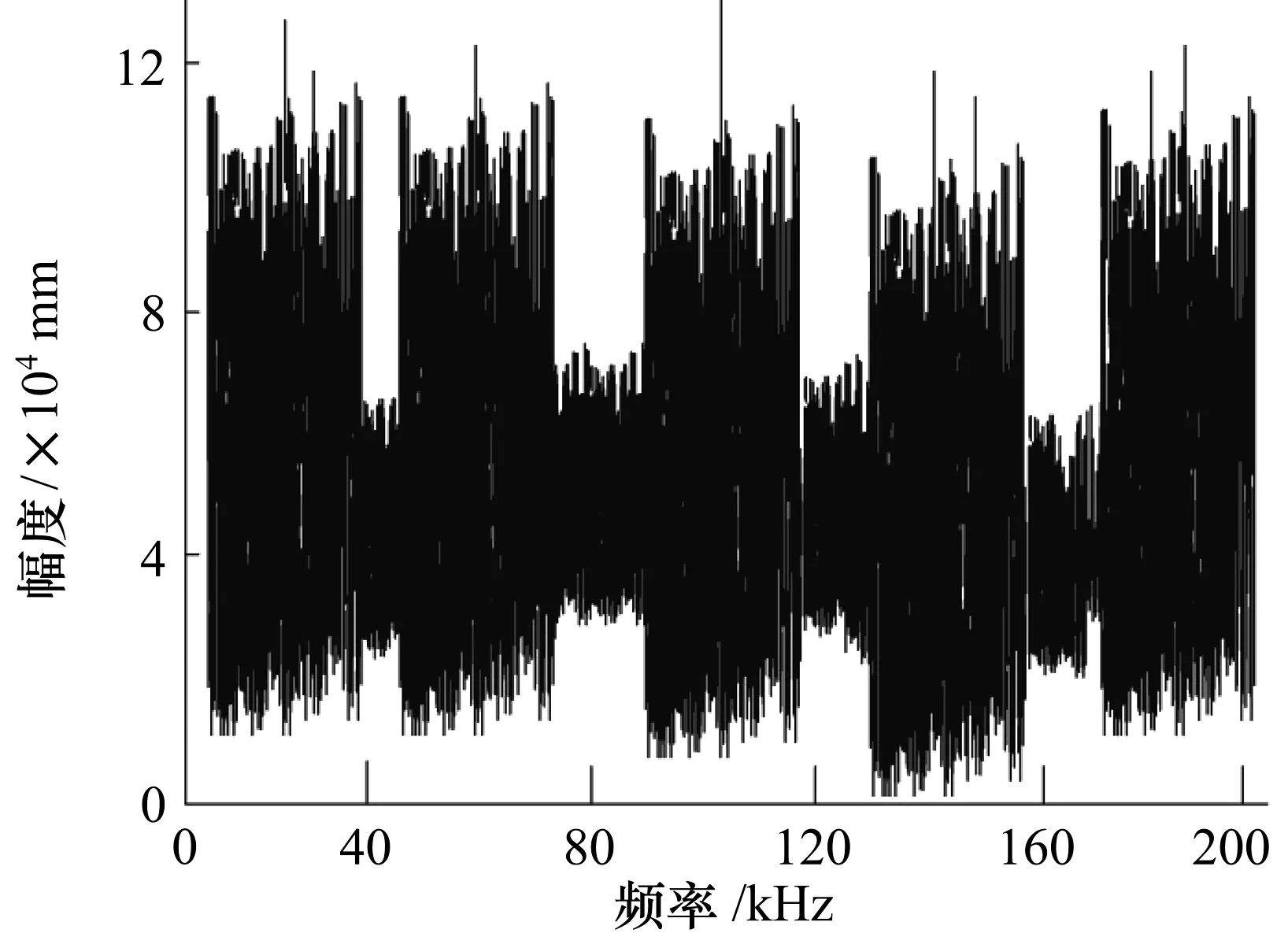
(a)梳状阻塞干扰信号
由图6可知,本文方法可有效分离实验通信系统源信号,成功将跳频信号与梳状阻塞干扰信号分离出,实现批量抑制物联网环境下多设备载波通信干扰的目标,提升了安全性。
3 结论
本文研究了一种物联网环境下多设备载波通信干扰批量抑制方法,解决了通信混合信号噪声干扰较大,影响通信传输安全性能的问题。实际应用结果表明,本文方法可有效降低通信噪声信号幅值,去噪效果较高,并由混合信号内成功分离出梳状阻塞干扰信号与跳频信号,实现对物联网环境下多设备载波通信噪声信号与梳状阻塞干扰信号的有效抑制,为物联网环境下多设备载波通信的运行提供了可靠的保障。

