考研数学背景下行列式计算的归纳解析

吕 军 库福立 黄 华

(新疆农业大学数理学院 830052)

行列式是线性代数中的基本内容,最初源于对线性方程组的求解,是由德国数学家莱布尼茨和日本数学家关孝和于17世纪先后提出.当然行列式的应用不仅在于求解方程组,在物理学、力学、工程技术等方面都有着重要的应用.

对于一般的低阶(二阶或三阶)行列式,可以直接利用对角线法则来计算,但对于高阶(四阶及以上)就没有那么简单.考生因高阶行列式的形式较为复杂,所以在计算时会感觉较为吃力.虽然高阶行列式结构较复杂,但是在计算时还是能够根据其自身具有的特点来选择适当的方法求解,这样会使其计算变得更加简单,起到事半功倍的效果.其实无论是低阶还是高阶行列式,其计算的中心思想就是“降阶”和“化零”.本文在其中心思想下对高阶行列式的计算进行了归纳总结,这样会使考生在面对高阶行列式时能够运用巧妙的计算方法,从而提高行列式计算的能力.

1 行列式的定义

定义1由n个自然数1,2,…,n组成的一个没有重复的有序数组i1i2…in称为一个n级排列.n级排列一共有n!个.

定义2在一个n级排列中，如果一个较大的数排在一个较小数之前，就称这两个数构成一个逆序.一个排列中逆序的总数,称为这个排列的逆序数，用τ(i1i2…in)表示排列i1i2…in的逆序数.

定义3由n2个元素aij(i,j=1,2,…,n)组成的记号

称为n阶行列式.其值是取自所有不同行不同列的n个元素的乘积a1j1a2j2…anjn的代数和,各项的符号由n级排列j1j2…jn所决定.即

2 行列式按行(列)展开定理

将n阶行列式中的元素aij所在的第i行和第j列的元素划掉，剩余的元素按原位置次序所构成的n-1阶行列式,称为元素aij的余子式,记为Mij.

Mij=

aij的代数余子式记为Aij,Aij=(-1)i+jMij.

设D=|(aij)n×n|为n阶行列式,则

则行列式的任何一行(或列)的所有元素分别与它们所对应的代数余子式的乘积之和为行列式的值.

3 几类行列式及其计算

3.1 抽象行列式

对于抽象行列式计算，不单单是考察行列式的计算，还涵盖了与行列式相关联的方阵、伴随矩阵、逆矩阵等.在计算时要对上述概念的运算性质熟练掌握.

例1若A∈R3×3,又A=(a1,a2,a3),且|A|=4.再设B=(a1+2a2,3a1+4a3,5a2),求|B|.

解对矩阵或行列式进行初等行(或列)变换,

|B|=4|(a1+2a2,3a1+4a3,a2)|=4|(a1,3a1+4a3,a2)|

=4|(a1,4a3,a2)|=20|(a1,a3,a2)|=-20|A|=-80.

3.2 n阶行列式

3.2.1 将行列式各行(或列)加到同一行(或列)中(适用于各行(或列)所有元素之和相等的情形).

解Dn=

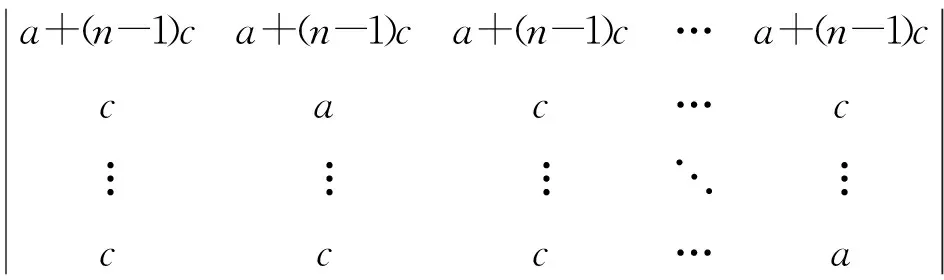
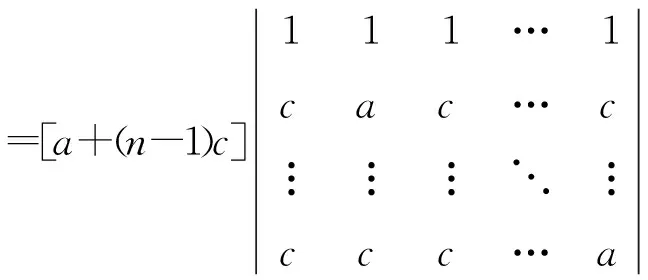
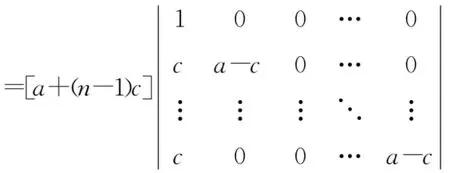
=[a+(n-1)c](a-c)n-1.

3.2.2 所求行列式某一行(或某一列)至多有两个非零元素(此时一般按此行(或此列))展开即可求解.

例3 计算n阶行列式

解行列式第一行,第一列均只有两个非零元素,现按第一列展开可得，

=xDn-1+an

由此递推可得：

注：用此方法求解时,一般会得到一个递推的关系式

Dn=pDn-1+qDn-2,

可用两种方法求出行列式Dn的表达式：

(1) 首先计算D1,D2,D3等,通过D1,D2,D3找出递推规律,再用数学归纳法进行证明即可；

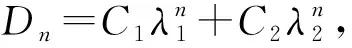
3.2.3 利用范德蒙德行列式的结果来计算行列式

范德蒙德行列式：

例4计算行列式

Dn=

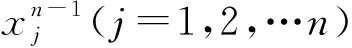
Dn=(x1x2…xn)n-1

由范德蒙德行列式可得：

总之,对于高阶行列式的计算,由于其变化形式较多,其相应的计算方法也较多.某一种方法可能只适用于某些具有一定特点的行列式,所以考生在面对不同形式的行列式时,首先应观察行列式所具有的特点,具体情况具体分析 ,从而体会、学习总结计算方法,通过练习,由浅入深,不断积累计算经验,从而进一步提高计算能力.