含动态元件的一般电路分析

曲仕齐， 胥 诺， 高昕悦

（西安交通大学电气工程学院，西安 710049）

0 引 言

采用结点电压法和拉普拉斯变换求解复杂电路时，通常因方程过于复杂，很难手工完成计算，利用Matlab等数学软件，计算机通过编程求解方程，可以大大减少人们的计算量［1-3］，同时利用Matlab等数学软件进行GUI界面设计使得电路中各结点电压波形可视化，可方便、直观地得到电路中各元件的电压［4-6］。

1 模型原理

1.1 结点电压法

结点电压是指电路中任意结点与参考结点之间的电位差，若电路可分为n个结点，任选一个结点作为参考点，令其电位为零，其余结点对该参考点的电位就是结点电压。以电路中结点电压为未知量，根据KCL写出独立结点电流方程，联立求解出各结点电压的方法为结点电压法［7-9］。

1.2 复频域分析法

采用经典的时域分析法分析计算高阶动态电路时，其初始条件和积分常数的计算非常复杂，使用复频域分析法则可以简化分析。其基本方法是将时域电路描述动态过程的常系数微分方程经拉氏变换转化为复频域的代数方程并求解，得到待求量的复频域函数，再经过拉氏反变换得到所求的时域响应［10-11］。

拉氏变换公式如下：

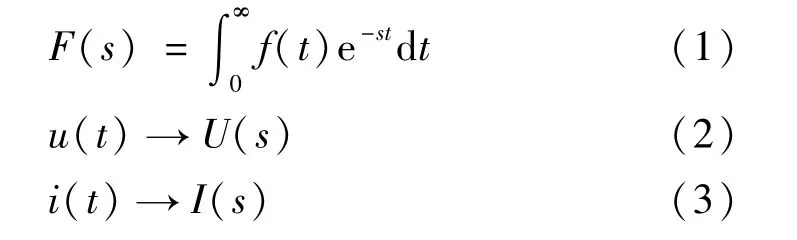
式中：t为时域变量；s为其拉氏变换后的复频域变量。

当电路为零状态响应时，有：

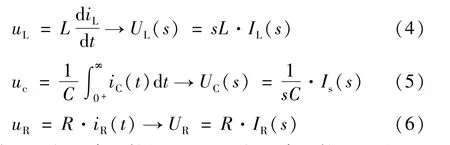
式中：uL为电感元件的电压；iL为电感元件的电流；uC为电容元件的电压；iC为电容元件的电流；uR为电阻元件的电压；iR为电阻元件的电流。

电路定理的形式变为：

若电路中电感、电容的初始值为0，则导纳Y变为：

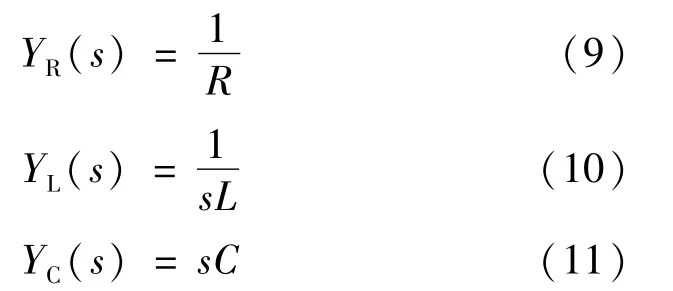
1.3 电路结构参数的存储

为实现电路的智能分析与计算，需要确定电路的结构、各元件的参数和初始条件等，列写对任意结构电路的结点电压方程，最后计算输出。

将不同电路的结构参数输入计算机，计算机根据输入参数自动列写结点电压方程。仔细研究手动列写结点电压方程的过程发现，结点电压方程与元件的类型、连接的起止结点及元件参数相关。

本程序能够进行智能分析的电路结构中的元件只涉及电阻、电流源、电压源、电感和电容5种（见表1）。其中电阻、电感、电容的编程思想类似，可作为一类元件，其参数有node1、node2、parameter，分别表示元件连接结点1、连接结点2、元件有效值，并将其拉氏变换形式存入导纳矩阵G（node1，node2）。电压源的参数有node1、node2、parameter、b、x，元件连接结点1、连接结点2、电压源幅值、电源频率、电压源初相，并将其拉氏变换后存入电压源矩阵U（node1，node2）。电流源的参数有node1、node2、parameter、b、x，元件连接结点1、连接结点2、电流源幅值、电流源频率、电流源初相，并将其拉氏变换后存入电流源矩阵I（node1，node2）。

表1 元件参数表

通过人机交互界面获取不同元件参数，并列写出不同结点的电路方程。以图1所示电路图为例说明过程。

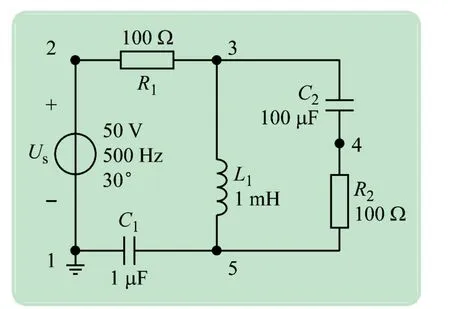
图1 示例电路图

各结点方程可简记为：

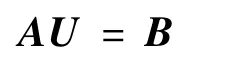
式中：A为系数矩阵；U为结点电压列向量；B为右端列向量。

当a，b两结点间为电阻、电感或电容时，有：

当a、b两结点是电压源时，将这两个结点合并成一个单独的“超级结点”，将流入、流出这两个结点的电流按照KCL一起处理，同时加上一个电压方程，写出这两个结点之间的电压关系。核心代码为：

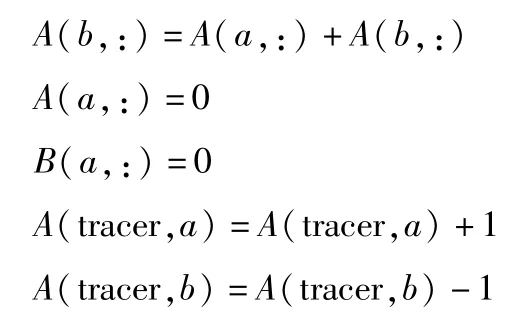
当a，b两结点是电流源时，

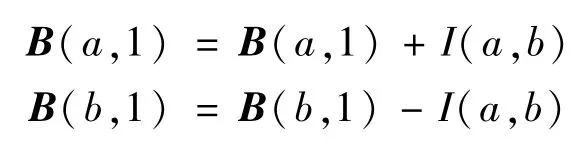
通过以上步骤可得：

对于上例中通过人机交互界面输入得到的矩阵有5个结点，将结点1列为参考结点，删除矩阵A的首行、首列，矩阵B的首行。并将A、B两矩阵联立，最终解出各结点电压U并作出波形图。

2 求解步骤

分析电路时采用结点电压法与复频域分析法相结合，其基本步骤如下：

步骤1确定电路结构、参考结点，输入总结点数，电源频率，输入各结点的元件参数，构建结点方程。

步骤2将各结点及增补的电压方程组合成矩阵形式，通过Matlab解出相应结点电压的复频域解，再经过拉式反变换得到所求时域响应。

步骤3输出所求时域响应并绘出图像。模型流程如图2所示。

图2 模型流程图

界面由3个模板部分组成，如图3所示。上方的初始量部分需输入电路的总结点数和电源频率，下方的元件部分可以根据电路结构进行元件的选择和输入相关物理量的大小，每当选择一个元件，输入相关的物理量大小后，点击“输入”按钮，元件会在右侧的显示部分出现，当添加完所有电路元件后，点击“计算”按钮，则出现各结点电压的表达式和图像。

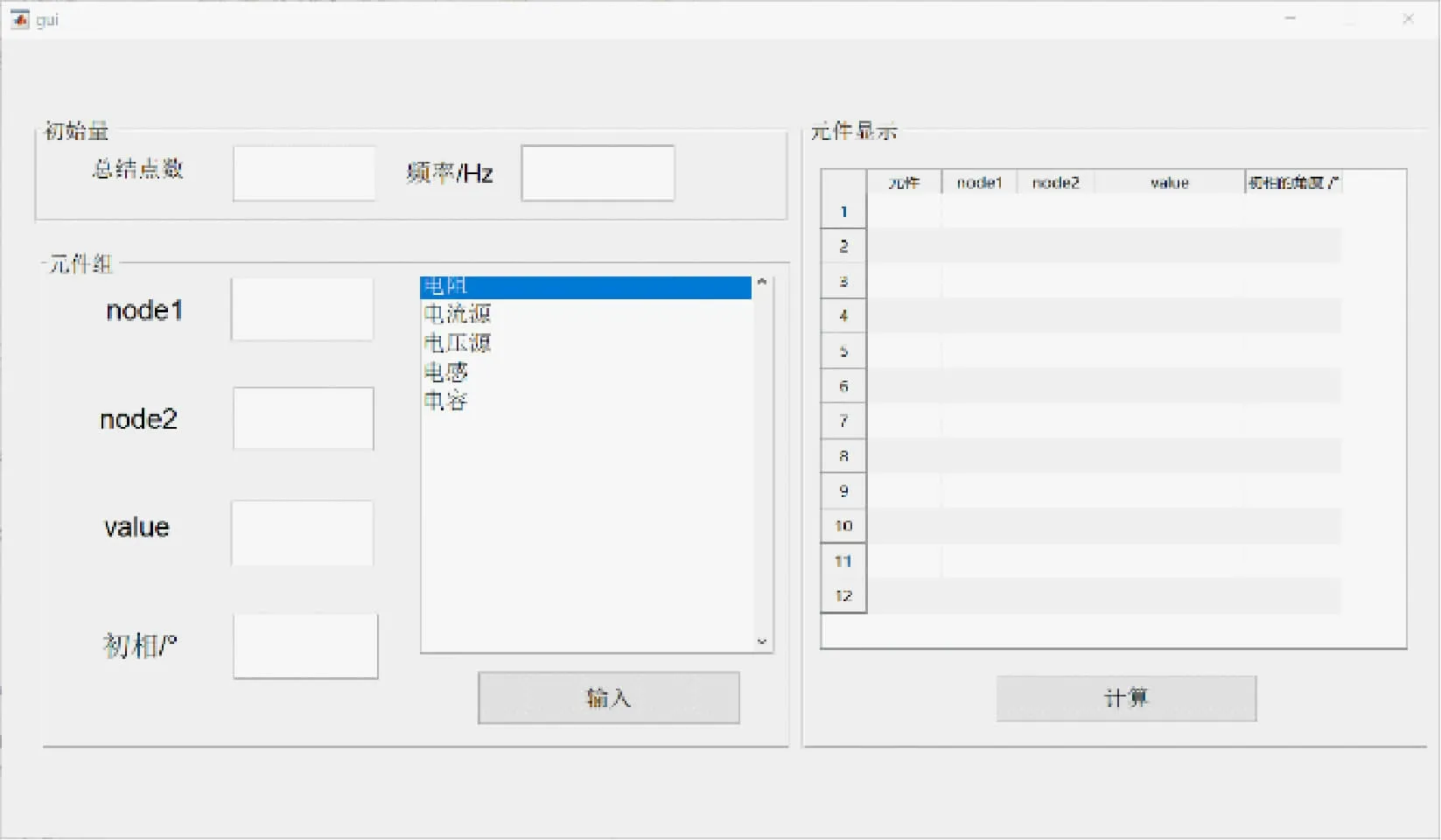
图3 输入界面图

3 算例分析

3.1 算例求解

利用结点电压法给电路中各结点标序号以方便输入Matlab程序中，以图4所示电路为例。

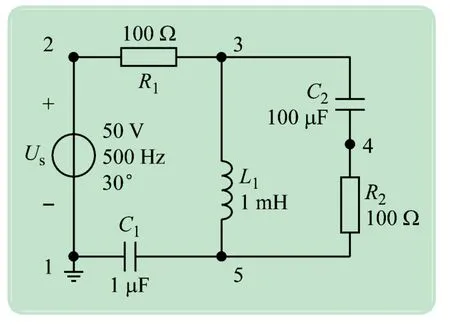
图4 算例电路原理图

根据结点电压法可给出各结点的方程，其中设结点1为参考结点，对结点2～结点6利用基尔霍夫电流定律（KCL）和拉氏变换可推导出各结点的结点电压方程。

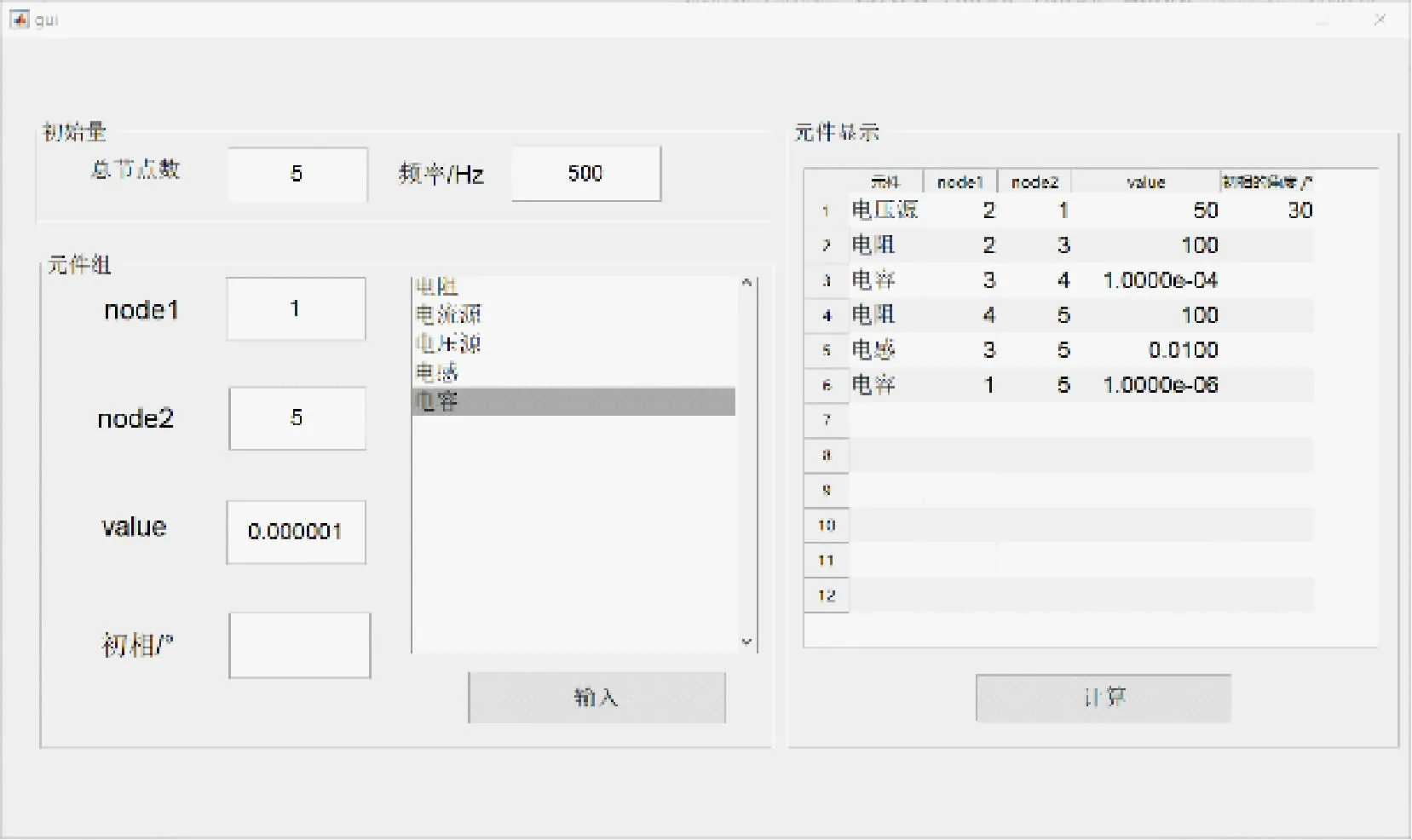
图5 输入界面

画出各结点电压的波形如图6所示。

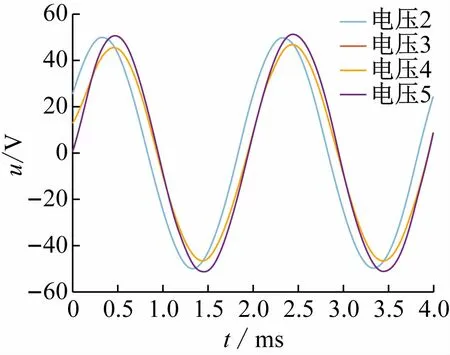
图6 测试电路各结点电压示意图

3.2 Simulink仿真模拟验证

Matlab中的Simulink具有强大的建模与分析功能，用Simulink建模验证较为方便［12-15］。本文用Simulink建立检验模型，并通过示波器来检查各结点电压的波形，通过对比分别检验模型的正确性，建立的模型如图4所示，用示波器显示结点3的电压，电压波形如图8所示。

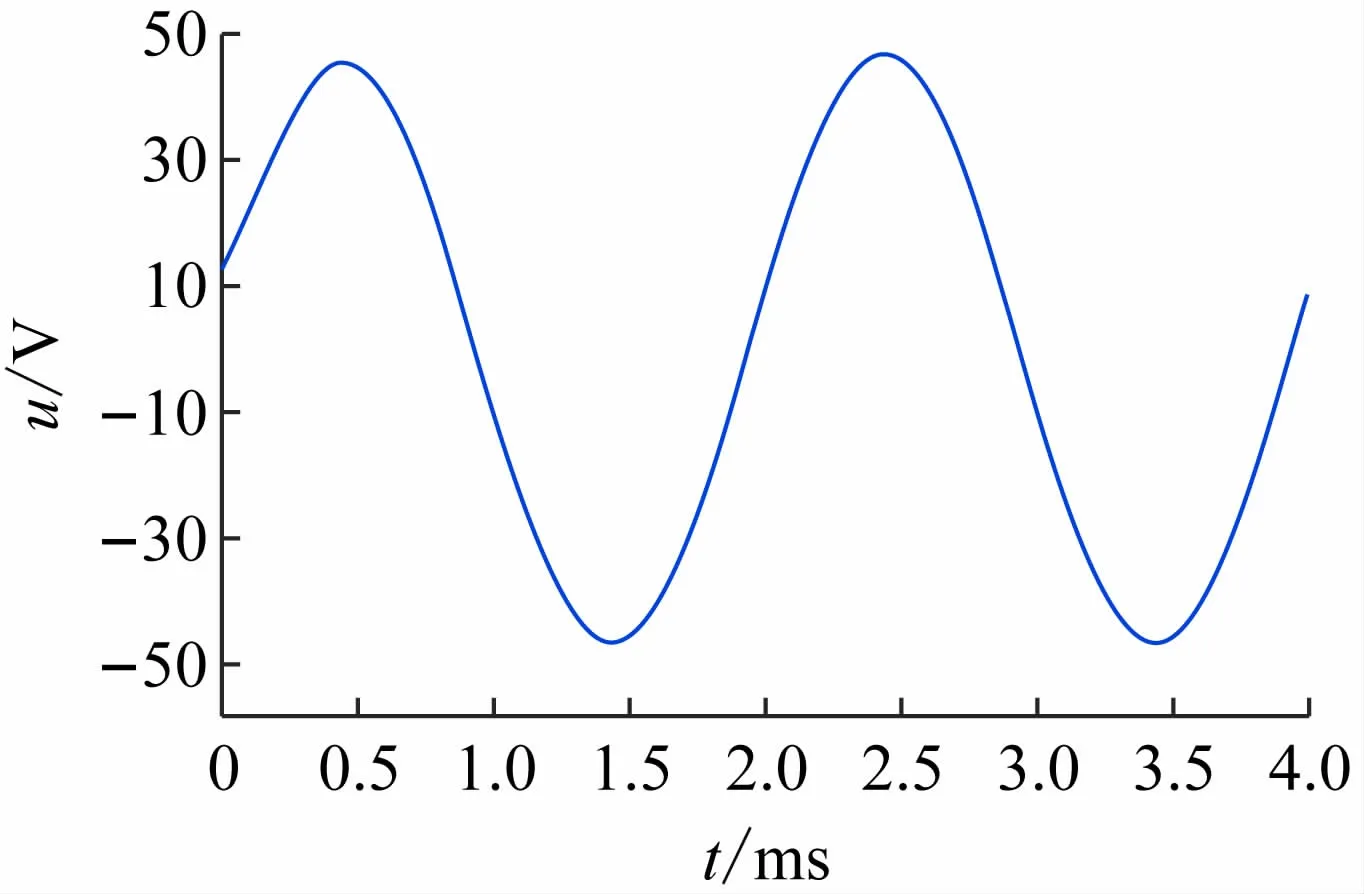
图7 结点3电压示意图

图8 结点3电压波形对比图

从两者的对比图中可以看出，通过模型计算绘出的波形与仿真的结果基本吻合，可以判断出模型的正确性。

4 结 语

对于复杂的含储能元件的一般电路分析，其暂态分析用复频域运算法较为方便，避免了高阶微分方程的求解；使用结点电压法和拉氏变换，便于解决复频域的分析问题。再利用Matlab的编程绘制功能计算并绘制各结点的电压波形即可。