基于FACT技术的高阶系统传递函数推导与降阶

张孝荟， 汤亚芳， 栗少龙， 宋 标， 袁旭峰

（贵州大学电气工程学院，贵阳 550025）

0 引 言

传递函数作为一种研究系统动态性能指标的重要手段［1］，在各行各业广泛应用。在控制系统中，为实现按照设计预期改变零、极点位置，达到调整系统结构、提高系统控制精度和稳定性的目的，应对复杂高阶系统的传递函数进行准确解析以及适当的降阶处理［2］。Vandeloo等［3］提出将电路模型参数导入编程软件Common Lisp中，利用稀疏矩阵进行传递函数的推导与化简的方法。但该方法严重依赖电路的具体参数，且所用编程语言过于专业，不具有普适性。文献［4］中利用Matlab软件仿真运算平台，以一个CMOS两级运算放大器电路为研究对象，对电路中各个晶体管的热噪声传递函数进行求解并简化，Matlab运算结果表明该方法能有效避免对电路参数的过分依赖。

文献［5］中对直流电动机复合定位控制系统CPCS及PID根轨迹、频率特性等动态性能进行分析，得出高阶系统的传递函数总能采用降阶方式化简的结论。高阶系统的降阶研究渗透在航空动力系统［6-7］、交通轨道磁悬浮控制系统［8］、柔性直流配电系统［9-10］等各个行业。然而，高阶系统传递函数的降阶处理过程往往会引起状态变量的改变，导致系统的控制精度下降，甚至影响系统稳定性。

鉴于上述技术进展及存在的问题，本文以柔性直流系统为背景，以文献［11］中所提混合式直流故障限流器拓扑结构为研究对象，利用快速分析技术（Fast Analytical Circuit Techniques，FACT）［12］对高阶系统传递函数进行推导和化简，并进行实验验证。特性［12］。

定义的传递函数表达式如下：

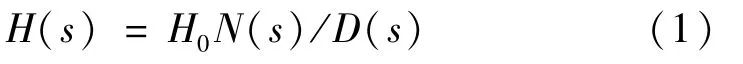
式中：H0为s＝0（电容开路、电感短路时，后续均设置s＝0作为电路参考状态）状态下的直流增益；零点为方程N（s）＝0的根，极点为方程D（s）＝0的根。图1为运用FACT求解高阶系统传递函数的流程图。

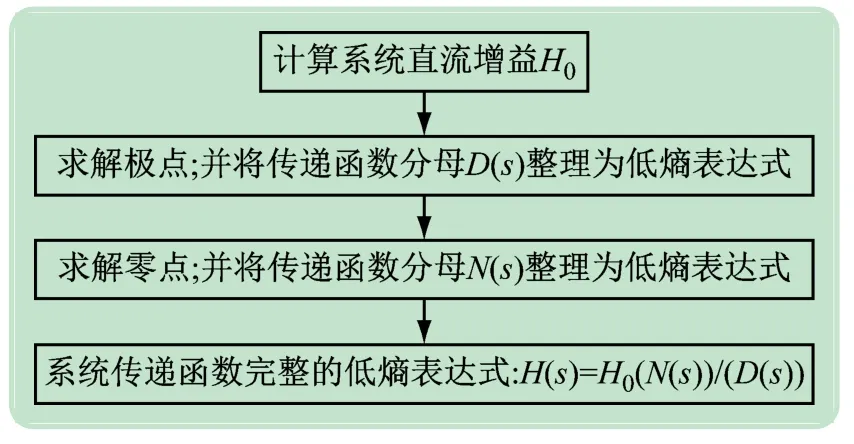
图1 FACT求解传递函数流程框图

1 高阶系统传递函数的推导与降阶

本文设计的基于FACT，利用时间常数表征电路特性的高阶系统传递函数求解过程：①根据FACT原理，首先将传递函数规范为低熵表达式；②将传递函数表达式整理为零、极点完美分离形式；③通过设计主导极点或偶极子［13］对高阶系统降阶，用降阶后的近似低阶系统，来表征原始复杂高阶系统的动态性能；④利用Matlab软件仿真运算取得系统降阶前后的单位阶跃响应曲线，验证该技术对高阶系统传递函数推导与降阶的有效性。

1.1 快速分析技术

利用FACT求解高阶复杂系统的传递函数，与传统方法相比，在求解速度方面具有显著优势。该技术主要特点如下：

（1）利用时间常数对电路进行表征。在特定条件下，暂时从电路中的连接端移除电阻、电感或电容元件，求得该端口的阻抗值，从而将复杂的无源电路或者有源电路分解为由一系列时间常数表征的零、极点网络［12］。

（2）低熵表达式。系统的熵与其内部紊乱程度相关联，利用FACT能够得到高阶系统传递函数的低熵表达式，可快速识别出系统增益、零点、极点，以及零、极点个数。分析传递函数的低熵表达式，能够明确串并联电路的主导器件以及不同频率状态下的电路

1.2 传递函数的推导

图2所示的混合式直流故障限流器工作原理为：故障后，保护系统检测到线路故障，立即给晶闸管T1送入触发脉冲，同时也给T2送入持续的触发信号；晶闸管T1导通瞬间，换相电容C1立即放电，放电电流导致T3断；C1放电完毕后继续被故障电流反向充电，一直被施加着触发信号的晶闸管T2，当其开始承受正向电压时瞬间导通。自此限流模块均被投入故障回路抑制故障电流。

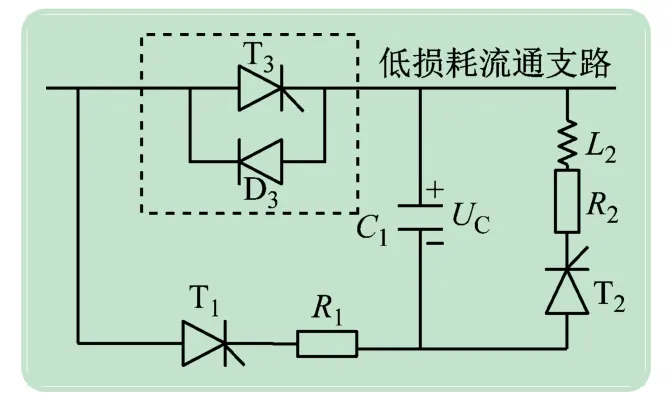
图2 混合式直流故障限流器拓扑结构

由上述限流原理可知：主限流支路中的R2在换相电容充电完毕后，方能完全投入故障回路抑制短路电流，故换相电容的反向充电时间越短越好。在限流过程中某个时刻，换相电容的初始电压放电完毕，并开始反向充电，从而进入另一个工作状态，直到其充电完毕。为进一步分析电容充电的暂态过程，故以换相电容两端的电压作为输出响应，利用FACT求解该系统传递函数。

如图3所示，用串联的电阻电感电容RS、LS、CS等效替代直流系统模块化多电平变换器（Modular Multilevel Converter，MMC）［14］，但该方法会导致系统的阶数升高，增加求解各阶段电压电流的详细表达式的难度。考虑到故障后短时间内MMC电容CS电压下降幅度较小，为方便求解，将其等效为恒定的直流电压源。文献［15-16］中对该等效方法进行了验证，认为误差较小，等效可行。忽略半导体器件通态压降，令RS＋R1＝R3，LS＝L3，其简化电路见图4。

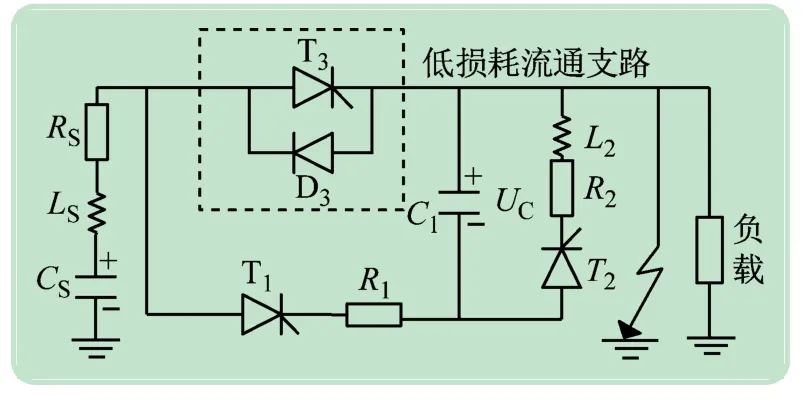
图3 电路模型

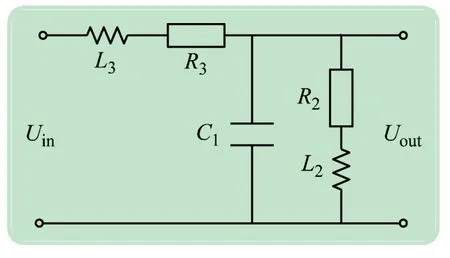
图4 电路模型简化图

依据FACT原理，可快速取得系统直流增益、零点推导、极点推导，以及完整传递函数的低熵表达式，大幅降低高阶系统传递函数推导的复杂性，提高了求解速度。

（1）直流增益。将各储能元件设置为参考状态（C1开路、L2短路、L3短路），计算直流增益为

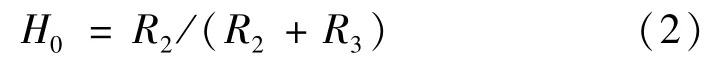
（2）极点推导。与电容C1、电感L2、电感L3相关联的时间常数τ1、τ1、τ3

［12］分别为：

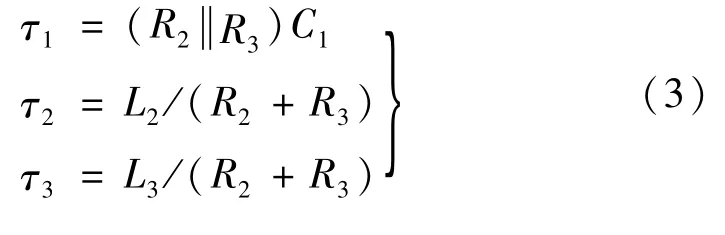
设［12］

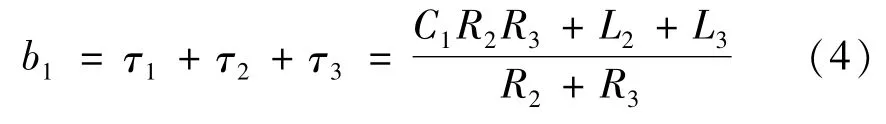
计算时间常数τ12、τ13、τ23时，分别看L2两端（C1为高频状态，L2、L3为参考状态）的驱动电阻、L3两端（C1为高频状态，L2、L3为参考状态）的驱动电阻、L3两端的驱动电阻（L2为高频状态，L3、C1为参考状态），得到：

设［12］

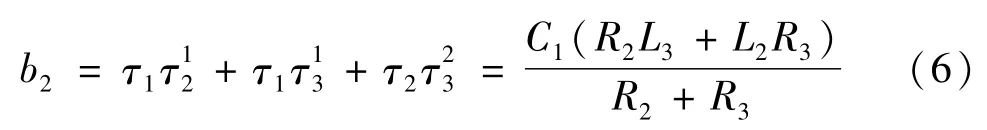
计算时间常数τ123［12］时，将C1、L2设置为高频状态（C1短路、L2开路），将L3设置为参考状态（L3短路），由L3两端的驱动电阻得到：

设［12］

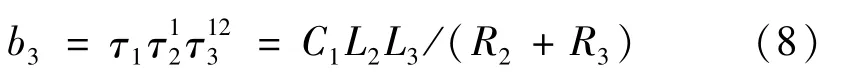
分母表达式D（s）［12］为

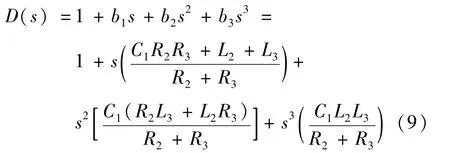
（3）零点推导。根据上述FACT求解传递函数分子表达式的过程与分母求解过程基本一致，唯一不同之处是：求解过程中需将激励源复原，输出置为零［12］。

具体过程，此处不再赘述。求解得到：

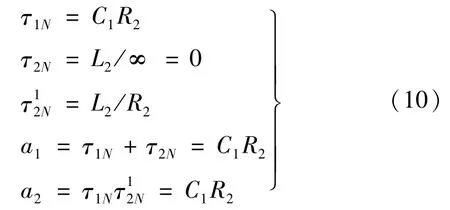
则，分子N（s）［12］表达式为

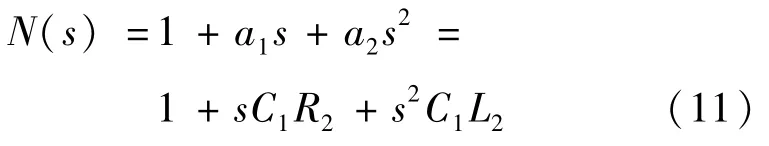
（4）完整表达式。由此可得到完整传递函数的低熵表达式［12］：

将传递函数的低熵表达式整理为零极点完美分离的表达式如下：

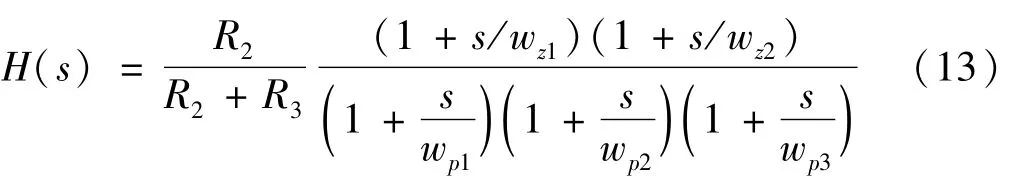
式中：

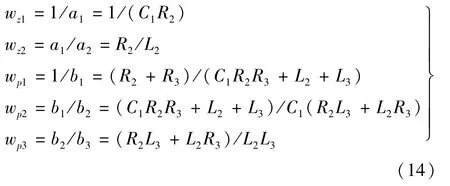
1.3 降阶处理

分析系统传递函数的零、极点，判断其是否满足降阶条件，具体流程如图5所示。

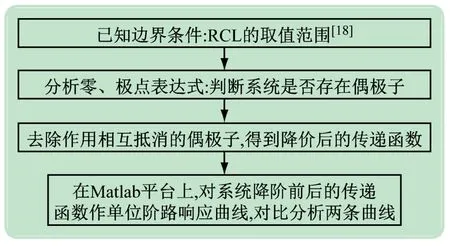
图5 系统降阶处理以及验证流图

令式（14）中零、极点的第1零点与第2极点的比值为A，则：

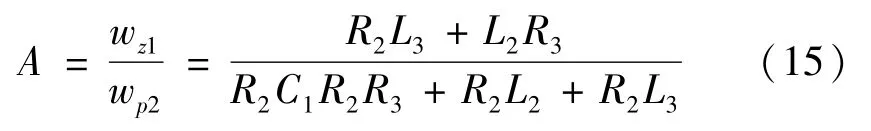
根据工程经验，确定参数一个初始取值范围：换相电容C1取值范围5～10 μF；限流电感L2取值范围10～30 mH；换流站系统等效电感L3取值范围150～200 mH；主限流电阻R2取值范围30～40 Ω；电阻R3其取值范围8～12 Ω。基于该取值范围，R2L3＞＞L2R3，R2C1R2R3＜＜R2L3＜R2L2，故：

同样，将第2零点与第3极点的比值令为B，则：

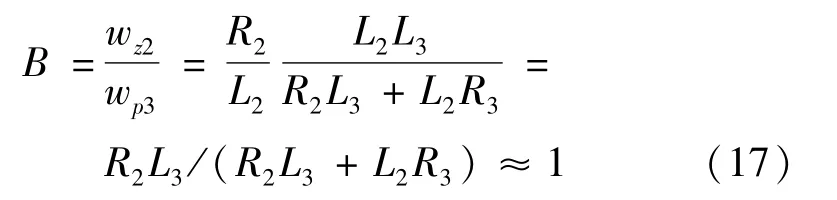
故系统传递函数中存在两对偶极子，分别为wz1和wp2、wz2和wp3，采用零、极点相消的方法对系统进行降阶处理［17］，去除两对偶极子，留下一个主导极点wp1，则最终将传递函数近似表达式如下：

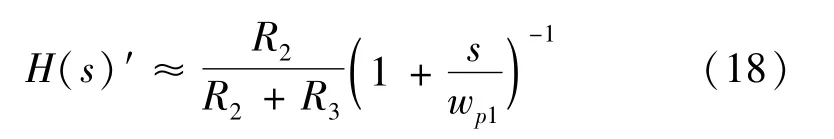
降阶后的传递函数近似等效为一阶系统，该系统时间常数为

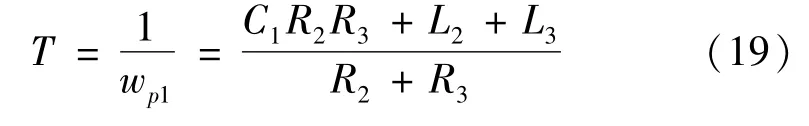
2 实验分析

2.1 降阶前

用Matlab（2017a）运算软件平台中自带的遗传算法工具箱，根据实际工程中限流器设备各储能元件常见的取值范围［18］，求取式（19）的最优解。图6（a）表明，利用遗传算法经过多次迭代之后，其适应度值基本不再变化，最终得到限流器设备各元件的最佳取值：C1＝10 μF，L2＝10 mH，L3＝150 mH，R2＝40 Ω；R3＝11 Ω；图6（b）为根据上述最佳取值求解式（19）的期望分布情况。

图6 遗传算法迭代优化参数

用Matlab求解原始高阶系统传递函数，主要程序如下：

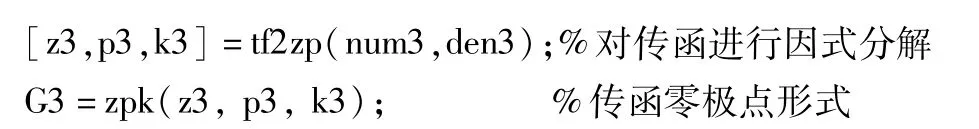
得到原始三阶系统的传递函数：

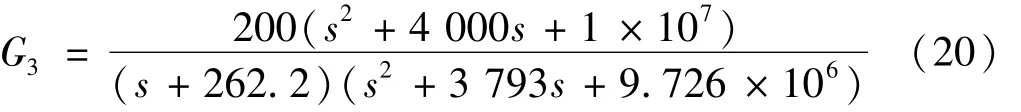
零极点分布如图7所示。

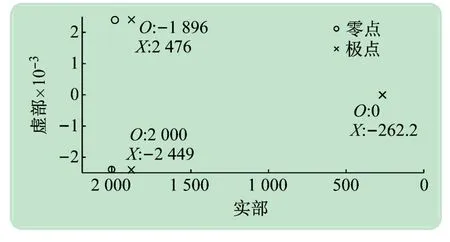
图7 零极点分布图

由图7可知，原始三阶系统存在两对偶极子，每一对偶极子的作用相互抵消，只剩一个主导极点作用，该系统满足降阶条件，与理论推导相符合。

2.2 降阶后

用Matlab对降阶后的系统求解传递函数，主要程序如下：

得到降阶后一阶系统的传递函数：

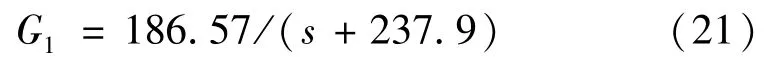
对比式（20）和（21）分析可知，降阶前后的系统主导极点分别为－262.2、－237.9，两个系统极点位置比较靠近。为验证降阶后的系统对原始系统的描述能力，在Matlab上绘制降阶前后系统的单位阶跃响应曲线，主要程序如下：

den3＝［b3 b2 b1 1］；

num3＝［a2 a1 1］*H0；

sys3＝tf（num3，den3）； %原始三阶系统建模

den1＝［b1 1］；

num1＝H0；

sys1＝tf（num1，den1）； %近似一阶系统建模

step（sys3，＇r＇，sys1，＇b＇）； %系统的单位阶跃响应曲线

图8表明两条单位阶跃响应曲线趋势基本一致，降阶后的系统其单位阶跃响应的上升时间tr比降阶前多0.89 ms，调整时间ts比降阶前多1.15 ms。这是因为降阶后的近似系统，其极点比降阶之前的主导极点更靠近虚轴，在一定程度上延缓了系统响应速度。

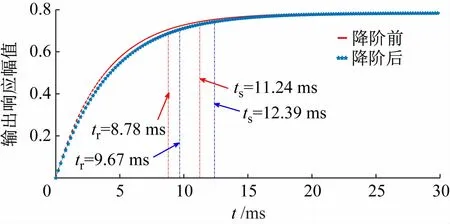
图8 降价前、后单位阶跃响应曲线

3 结 语

本文利用FACT对高阶系统传递函数进行详细推导表明：得到传递函数的低熵表达式，能更直观地识别出系统直流增益、零点、极点；通过观察传递函数表达式能够明确串并联电路中的主导元件以及电路频率特性；对传递函数的零极点表达式进行分析和约束，构造降阶条件，将复杂高阶系统近似等效为简单低阶系统。用Matlab运算软件对降阶前后的传递函数作单位阶跃响应仿真运算，结果验证了上述传递函数求解方法、系统降阶方法的有效性、合理性。

在工程运用中，按照FACT原理简化求解过程、降低求解难度，进而提高传递函数求解速度，该技术具有一定的普适性。