桥上CRTS II型板式无砟轨道参数对轨道结构振动响应的影响
房建,杨敏超,雷晓燕,练松良
(1.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室,江西 南昌 330013;2.同济大学 道路与交通工程教育部重点实验室,上海 201804)
截至2020年底,我国高速铁路运营里程达3.79万km,较2015年末的1.98万km,相当于在“十三五”期间翻了近一番,稳居世界第一。高速铁路在给人们出行带来便利的同时,也带来了一系列负面问题,以轨道振动问题尤为突出[1]。在列车荷载作用下,轨道结构产生的振动与轨道参数密切相关,深入研究轨道参数对轨道结构振动特性的影响,有助于实现对轨道结构振动问题的有效控制。当前,国内外很多学者从轨道结构振动响应方面对车辆—轨道耦合动力学问题进行了分析[2-10],王相平等[11]基于车-线-桥相互作用,采用Non-elliptical轮轨接触模型和Archard材料磨损理论,探究了含扁疤车轮轮轨磨耗对车辆-轨道-桥梁系统动力学性能的影响规律。罗惠峰等[12]基于动力学软件Simpack建立CHR2型高速车辆-板式无砟轨道模型,通过对原有单层轨道拓扑优化后设置分层,分析了轨下弹性扣件刚度和阻尼对板式无砟轨道结构动力特性的影响。徐金辉等[13]建立CRTSⅡ型板轨道垂向耦合系统动力分析模型,将频率分析法与辛数学方法相结合进行求解,在频域内分析了轨道板厚度、混凝土支承层厚度、扣件系统刚度和阻尼、CA砂浆弹性模量和阻尼对高速车辆响应的影响。以上研究多集中于路基形式的轨道结构,针对高速线路高架轨道结构的振动特性研究较少。本文基于高速车辆-CRTS II型板式无砟轨道-桥梁耦合振动分析的有限元模型,从时、频域研究轨道结构参数对桥上CRTS板式轨道结构振动特性的影响。
1 车辆-轨道-桥梁动力学分析模型
根据车辆-轨道-桥梁耦合作用的特点,本文将列车、多跨连续梁桥上CRTS II型板式轨道以及桥梁视为一个整体系统,建立车辆-轨道-桥梁垂向耦合动力学分析模型。
利用有限元法及Lagrange方程,提出2种新型单元,即新型车辆单元与新型轨道单元;同时推导了2种单元的刚度矩阵、质量矩阵以及阻尼矩阵。新型车辆单元是将一节车辆离散为一个车辆单元,与传统单元不同的是,车辆单元每个车轮下附一系钢轨,该钢轨用于车辆与轨道之间的耦合,不计其质量和刚度。
车辆通常由车体、转向架和轮对三部分经弹性悬挂和阻尼元件相互联结而成。本文选用多节移动CHR 3型动车,采用整车附有二系弹簧质量车体模型,单节车辆模型见图1。

图1 整车车辆单元模型Fig.1 Modelof vehicle
轨道单元是根据桥上CRTSⅡ型板式轨道结构中轨道板、底座板跨梁缝连续铺设的特点,考虑钢轨、轨道板、混凝土支承层和桥面板以及相互作用关系的4层梁模型,如图2和图3所示。该4层梁模型,从上到下分别为钢轨、轨道板、混凝土支承层和桥梁。图中,v1,v5表示钢轨的竖向位移;θ1,θ5表示钢轨的转角;v2,v6表示轨道板的竖向位移;θ2,θ6表示轨道板的转角;v3,v7表示混凝土支承层的竖向位移;θ3,θ7表示混凝土板支承层的转角;v4,v8表示桥梁单元的竖向位移;θ4,θ8表示桥梁单元的转角。
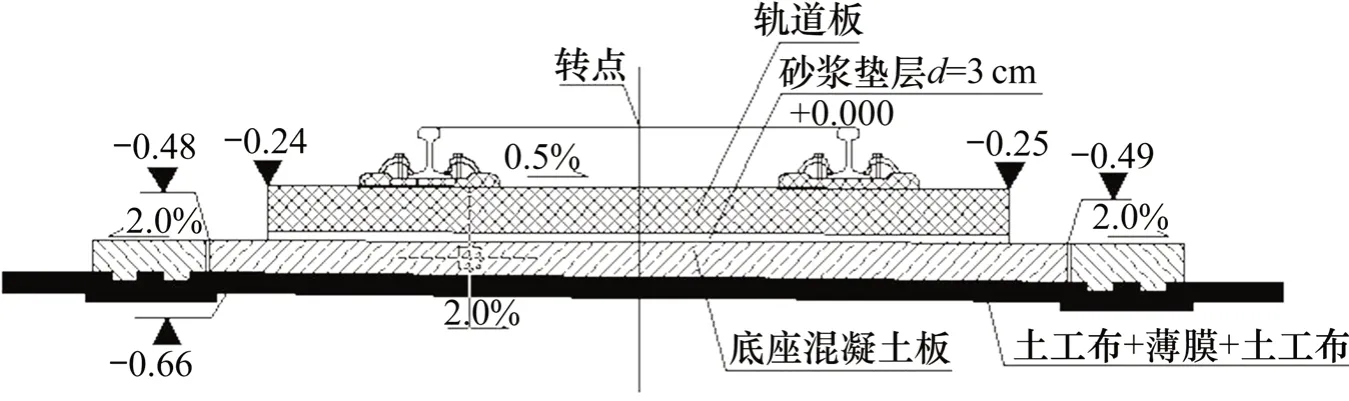
图2 桥上CRTSⅡ板式轨道Fig.2 CRTS IIslab track structure on bridge
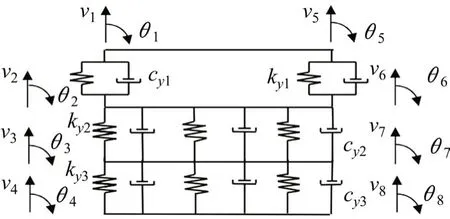
图3 桥上CRTSⅡ板式轨道单元的4层梁模型Fig.3 Four-layerbeam modelof CRTS IIslab track structure on bridge
运用以上新型车辆-轨道单元,建立轨道不平顺作用下车辆-高速线路桥上CRTS II型轨道-桥梁系统耦合振动有限元分析模型,并编制了计算程序。模型的计算结果与文献[14]对比,吻合较好,证明了模型的有效性。基于所建立的模型,本文研究了桥上CRTS II型板式轨道结构参数对轨道振动的影响。车辆为CHR 3型高铁车辆,运行速度为250 km/h。计算车辆-轨道-桥梁耦合模型的振动响应时,将合-武客运专线无砟轨道实测不平顺作为轨道不平顺激励,其中轨道不平顺实测样本如图4所示。

图4 实测轨道不平顺样本Fig.4 Sample ofmeasured track irregularity
2 不同钢轨类型对轨道结构振动特性影响
针对CN43,CN50,CN60以及CN75不同类型钢轨,计算实测不平顺条件下轮轨相互作用力以及钢轨、CRTS II轨道板和桥梁振动加速度幅值如表1所示,钢轨、CRTS II轨道板和桥梁振动加速度级如图5所示。

表1 钢轨类型变化对振动响应的影响Table 1 Effectof rail type changeson vibration response
表1表明,在相同轨道不平顺条件下,钢轨类型由CN43依次向CN50,CN60和CN75改变时,钢轨、轨道板及桥梁振动加速度呈减小趋势,表明随钢轨质量、惯性矩变大,动态轮轨力与动力响应也相应减小。图5表明,在分析频率范围内相对于CN75钢轨,采用CN60钢轨、CN50钢轨和CN43钢轨时钢轨振级平均增大了2,2.7和4.53 dB,说明重型钢轨有助于减小钢轨的振级。轨道板振动主要集中在50 Hz以下的频率范围内,改变钢轨的类型对降低轨道板的振动水平虽然有一定效果,但不是很明显。桥梁振动级受钢轨类型的影响较小,说明采用重型钢轨可以降低钢轨的振动水平,对降低轮轨噪声具有一定的意义[15]。

图5 钢轨、轨道板与桥梁振级1/3倍频曲线Fig.5 1/3 octave spectrum curvesof rail,railplate and bridge vibration
3 不同扣件刚度对轨道结构振动特性影响分析
对应于扣件系统刚度分别为25,35,60,100和160MN/m时,实测轨道不平顺条件下轮轨作用力以及钢轨、CRTSII轨道板和桥梁振动加速度幅值如表2所示;钢轨、CRTS II轨道板和桥梁振动加速度级如图6所示。
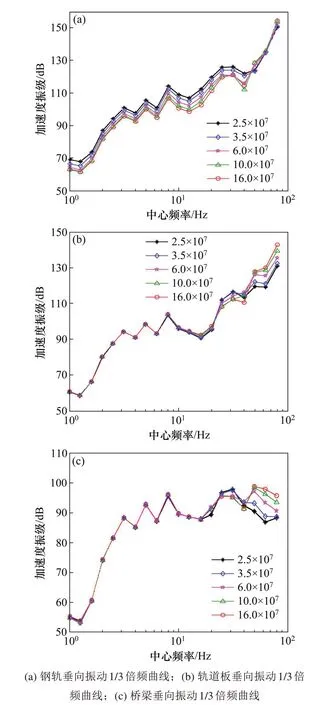
图6 钢轨、轨道板与桥梁振级1/3倍频曲线Fig.6 1/3 octave spectrum curvesof rail,rack slab and bridge vibration

表2 扣件刚度变化对振动响应的影响Table 2 Effectof supporting slab stiffnesson vibration response
表2表明,在相同轨道不平顺条件下,动态轮轨力、轨道结构振动加速度随扣件刚度的增大而增大。图6表明,钢轨振动水平在1~40Hz范围内随扣件刚度的增加而减小;但在40~100 Hz范围内,钢轨的振动水平随着扣件刚度增加而增大。对轨道板而言,在1~25 Hz范围内,振动级基本上不随扣件刚度的增大而变化,受扣件刚度的影响较小;在25~100 Hz范围内,轨道板的振动水平随扣件刚度减小而减小,平均减小3.5 dB,减振效果随扣件刚度的减小而增加。对桥梁而言,在1~16 Hz范围内,扣件刚度的变化对振动级影响不大;但在40~100 Hz范围内,振动级随着扣件刚度的减小而减小,表明减振效果随扣件刚度的减小而增大。由此可得,在40~100 Hz范围内减小扣件的刚度可以减小轨道板、桥梁的振动水平,但会增大钢轨的振动水平。
4 轨道板厚度对轨道结构振动特性影响分析
对应于轨道板厚度为0.15,0.2,0.3和0.45m时,钢轨、CRTS II轨道板和桥梁的振动加速度幅值及轮轨相互作用力均值如表3所示;钢轨、CRTS II轨道板和桥梁的振动加速度级如图4所示。

表3 轨道板厚度变化对振动响应的影响Table 3 Effectof variations in track plate thicknesson vibration response
表3表明,对相同轨道不平顺条件,轨道板厚度变化对轨道结构振动响应影响不大。当轨道板的厚度从0.15m变化到0.2m和0.3m时,轮轨作用力减小0.01 kN和0.02 kN;钢轨加速度减小0.5m/s2和1.3m/s2,轨道板的振动加速度分别减小4.4 m/s2和4.5 m/s2,桥梁的振动加速度分别减小0.4 m/s2和3 m/s2。当轨道板厚度从0.3 m变化到0.45m时,轮轨力增大0.41 kN,钢轨的振动加速度增大9.8 m/s2,轨道板的振动加速度增大1.0m/s2,桥梁的振动加速度增大2.66m/s2。图7表明,钢轨振动级在20~40Hz范围内随着轨道板厚度增大而小幅减小,在40~250 Hz范围内随着轨道板厚度增大而增大,这主要是因为轨道板厚度增大一方面增加了轨道质量,另一方面又提高了轨道板的抗弯刚度。当轨道板厚度从0.15m依次增大为0.30,0.45和0.9m时,轨道板的振动级减小3.14,4.9和7.2 dB;桥梁的振动级在20~250Hz范围内减小2.8,4.6和6.3 dB。

图7 钢轨、轨道板与桥梁振级1/3倍频曲线Fig.7 1/3 octave spectrum curvesof rail,railplate and bridge vibration
5 轨道板支承刚度对轨道结构振动特性影响分析
对应于轨道板支承刚度分别为100,150,250和400MN/m时,钢轨、CRTS II轨道板和桥梁的振动加速度幅值及轮轨力均值如表4所示;钢轨、CRTSII轨道板和桥梁的振动加速度级如图8所示。
表4表明,对相同轨道不平顺,轮轨力受轨道板支撑刚度变化的影响较小;钢轨加速度随着轨道板支撑刚度的增大而轻微减小,轨道板与桥梁的振动加速度随轨道板支撑刚度增大而变化的规律不明显。图8说明,在12.5Hz以下以及60Hz以上频率范围内,钢轨振动级受轨道板支承刚度的影响较小;在12.5~60 Hz范围内随轨道板支承刚度的增大,钢轨的振动级分别增加3.6,4.1和5 dB。轨道板振动级在60 Hz以下的频率范围内随轨道板支撑刚度的增大而减小,平均减小2.2,3.4和4.6 dB;在60~200 Hz范围内随轨道板支承刚度的减小而轻微减小,在200 Hz以上的频率范围内变化较小。当轨道板支承刚度从100MN/m变化到150,250和400 MN/m时,桥梁的振动级在20~200 Hz范围内平均增大3.5,5和6.6 dB,随轨道板支承刚度的增大而增大。表明了降低轨道板的支承刚度可在小幅度影响轮轨力的前提下较大幅度减小桥梁振动,因此具有一定减振降噪效果。
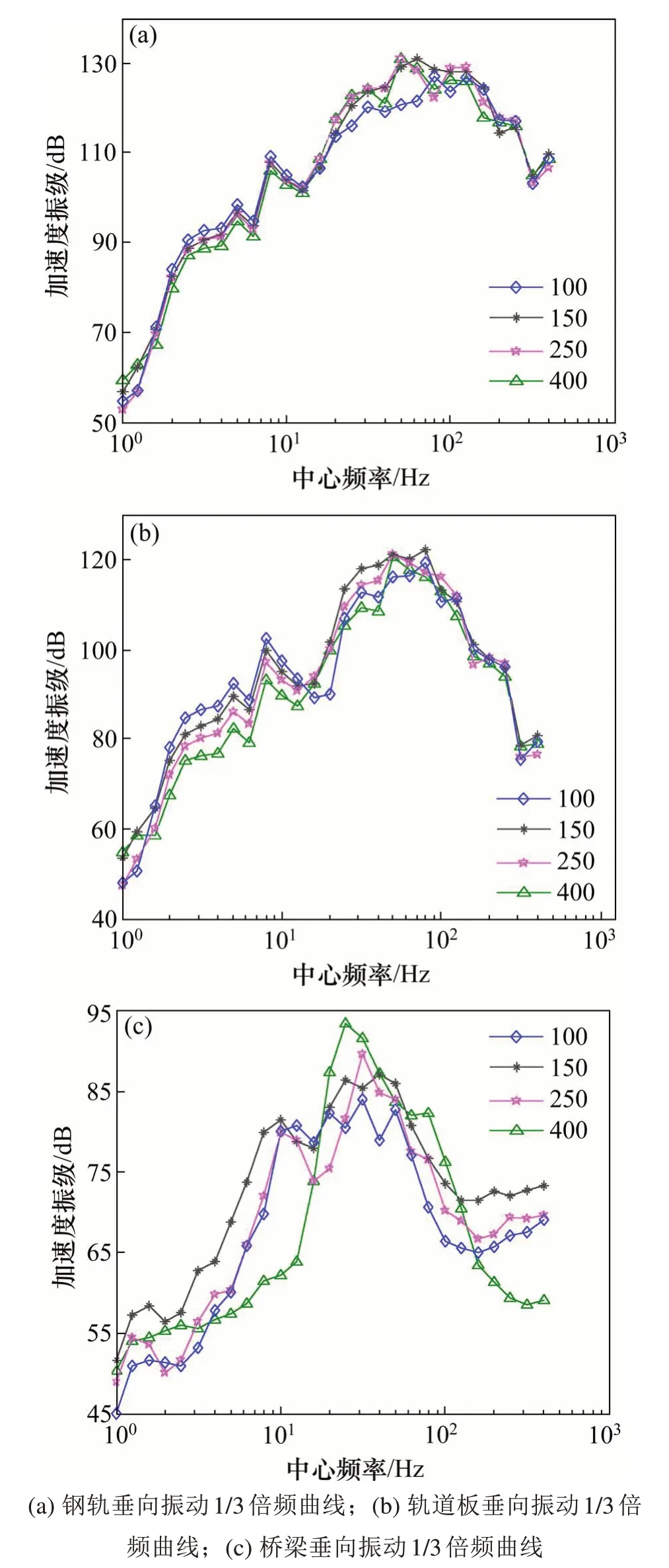
图8 钢轨、轨道板与桥梁振级1/3倍频曲线Fig.8 1/3 octave spectrum curvesof rail,railplate and bridge vibration
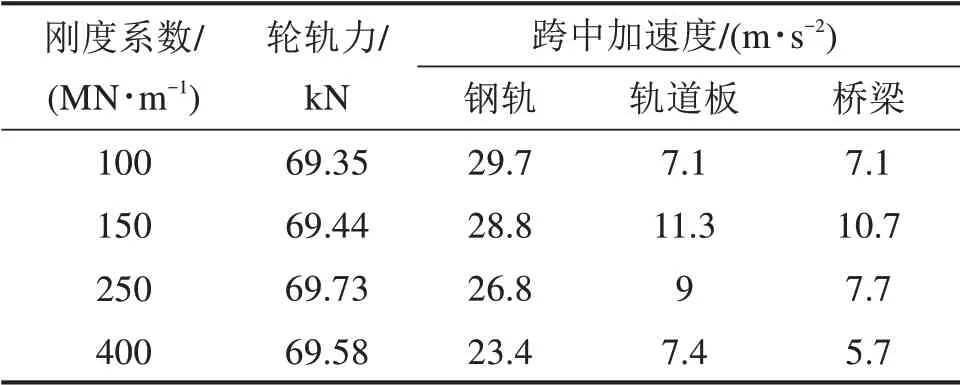
表4 轨道板支撑刚度变化对振动响应的影响Table 4 Effectof change in track plate supportstiffnesson vibration response
6 结论
1)相同轨道不平顺作用下,钢轨质量和惯性矩增大可以降低轮轨力,钢轨和轨道板的振动级在分析频率范围内随着钢轨质量、惯性矩的增大而减小,桥梁的振动级受到钢轨类型的影响较小,说明采用重型钢轨可以降低钢轨的振动水平,对降低轮轨噪声具有一定的积极意义。
2)降低扣件刚度在40~100 Hz频率范围内可以减小轨道板、桥梁的振动水平分别为1 dB和3.5 dB,但将会导致钢轨振动水平增大。钢轨振级在10~80 Hz频率范围内随垫板阻尼的增大而增大,轨道板的振动级在40~80 Hz和250~400 Hz频率范围内随垫板阻尼的增大而减小,桥梁的振动级受到垫板阻尼变化的影响很小。
3)随着轨道板厚度增大,钢轨振级在60~250 Hz频率范围内减小,在2.5~60 Hz范围内增大;轨道板振级在60 Hz以上的频率范围内随轨道板厚度的增大而减小;桥梁的振动级在20Hz以上的频率范围内随轨道板厚度的增大而减小。

