基于总体最小二乘的灰色模型在基坑沉降预测中的应用
雷前坤
(遵义黔通达检测试验有限责任公司, 贵州遵义 563000)
目前,变形预测中常采用的方法有回归分析法、时间序列法、灰色模型等[1]。其中,灰色模型对时间序列短、统计数据少、信息不完全系统的建模与分析,具有独特的优越性,在变形预测领域得到广泛应用[2-7]。传统灰色模型对于原始数据序列之后的1~2期数据具有较高的预测精度,随着预测期数的增加其精度会越来越低。针对传统灰色模型的不足,引入了动态灰色模型,一方面它继承传统灰色模型的优点,另一方面又及时去掉数据序列中失去预测意义的老数据的同时又加入最新的数据,不断更新,从而提高了模型预测的精度。动态灰色模型根据加入的信息不同分为2种:①若加入的是预测值,则称为灰色递补动态预测模型;②若加入的信息为实测值,则称为新陈代谢灰色预测模型[6-7]。无论是传统灰色模型还是动态灰色模型,传统的方法都是采用经典最小二乘对模型进行解算。由于灰色模型中的系数矩阵部分元素是由观测数据构成的,因此系数矩阵中也必然含有误差,因而采用经典最小二乘进行解算,由于无法顾及系数矩阵中的误差,得到的结果不是最优的。总体最小二乘在解算模型参数时,能顾及到系数矩阵中的误差[8-9]。基于此,文中利用总体最小二乘来求解灰色模型中的灰参数。文中以一基坑沉降监测数据为例,分别采用经典最小二乘和总体最小二乘对几种灰色模型的参数进行求解,并进行沉降建模预测分析,得出有益结论。
1 模型建立
1.1 传统灰色模型
传统灰色模型建模过程[6-7],设非负离散等间隔数列为:
(1)
对其进行一次累加得到:
(2)

对X(1)建立一阶白化微分方程:
(3)
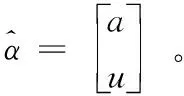
系数矩阵及观测向量如下。
(4)
(5)
采用最小二乘法,解算得到参数:
(6)
将参数带回白化微分方程可得:
(7)
对上式进行累减计算可以得到:
x(0)(n+1)=x(1)(n+1)-x(1)(n)
(8)
从而可以得到模拟值或预测值:
(9)
1.2 动态灰色模型

1.3 基于总体最小二乘的灰色模型
从灰色模型的系数矩阵的结构可以看出,其第一列是由观测数据累加得到的,由于观测量不可避免的含有误差,故系数矩阵中必然含有误差。因此,如果忽略系数矩阵中的误差,得到的结果是不合理的,且理论上也不完善。根据文献[9],设α为待估参数,Yn为观测向量,C为系数矩阵,EC为系数矩阵C中的误差矩阵,eY是观测向量中的误差向量,则有:
Y+eY=(C+EC)α
(10)
将增广矩阵进行奇异值分解:
(11)
式中:
总体最小二乘解可由增广矩阵右奇异向量的最后一列求得,即参数α的估值为
(12)

2 算例分析
取文献[10]中的算例数据。表1为一基坑6号点2015年10月24日至2015年11月15日的12期沉降监测值,利用前7期的沉降监测数据建立模型,后5期的沉降监测数据作为预测的参考值。表2统计了采用的方案,表3为实测值与各种方案所得到的预测值,表4为相对误差及均方根误差(RMSE)统计结果。为了更直观的比较各种方案的预测结果,将实测值与各种方案所得预测值绘制成图1和图2。
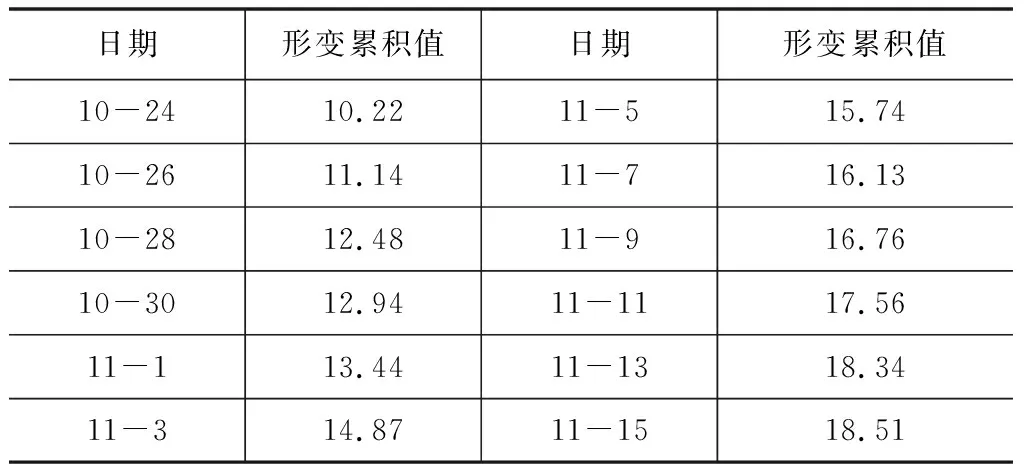
表1 沉降实测值 单位:mm

表2 采用方案
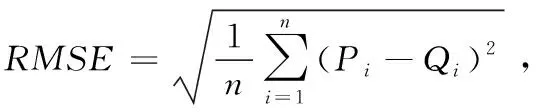
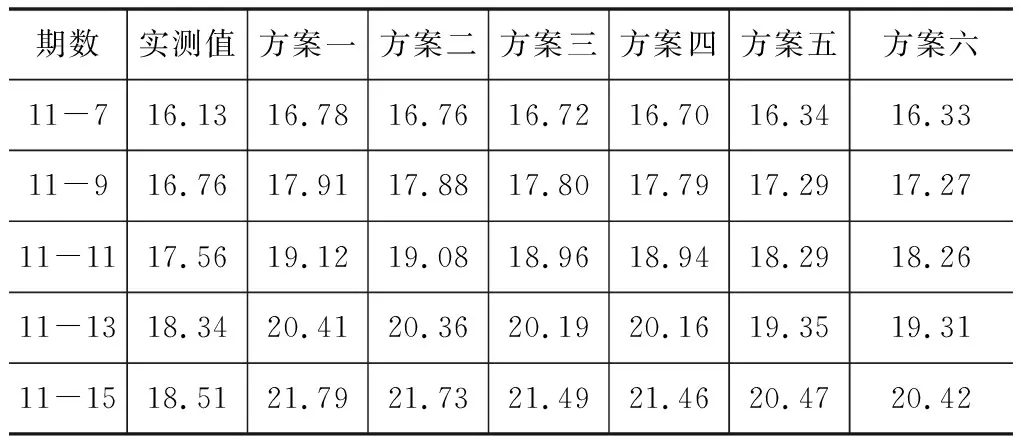
表3 实测值与各方案预测值 单位:mm

表4 相对误差

图1 实测值与经典最小二乘解算预测值

图2 实测值与总体最小二乘解算预测值
分析表3、表4、图1和图2,可得出结论:
(1)表3中,从基于经典最小二乘的预测结果来看,新陈代谢灰色预测模型预测得到的结果更接近实测值,灰色递补动态预测模型的预测结果次之,传统灰色模型的预测结果最差。采用总体最小二乘解算后进行建模预测,各种模型预测得到的预测结果相对于经典最小二乘都有所提高,其中又以基于总体最小二乘的新陈代谢灰色预测模型预测得到的结果为最优。以上表明,采用总体最小二乘来求解灰色模型中的灰参数,可以提高模型的预测精度。
(2)表4中,从平均相对误差和均方根误差来看,平均相对误差和均方根误差最大的为传统灰色模型,其平均相对误差为9.76%,均方根误差为3.84 mm,最小的为基于总体最小二乘的新陈代谢灰色预测模型,其平均相对误差和均方根误差分别为4.78%和1.08 mm,结果明显小于传统灰色模型,其余预测模型的平均相对误差和均方根误差按方案表顺序依次递减。以上表明,基于总体最小二乘的新陈代谢预测模型的预测精度要高于其他5种模型。
(3)从图1和图2中实测值与各种模型的预测值曲线来看,基于总体最小二乘的新陈代谢灰色预测模型的预测值曲线走向与实测值更加接近,但11月15日第5期的预测值曲线走向却发生了较大变化。这表明,虽然采用总体最小二乘来求解新陈代谢灰色预测模型中的灰参数能在一定程度上提高模型的预测精度,但预测期数不宜过长,从本算例来看,控制在4期以内的预测结果较为理想。这也表明,在实际沉降预测工作中,应根据预测值与实测值的具体情况,采用新的数据序列重新建立新的预测模型进行预测,以提高预测结果的精度。
3 结 论
基于经典最小二乘解的灰色模型由于无法顾及系数矩阵中的误差,致使建立的预测模型精度不高,本文利用总体最小二乘来解算灰色模型中的灰参数,提高了模型的预测精度。综合本文研究结果,得出几点结论和建议:
(1)从模型预测结果来看,新陈代谢灰色预测模型更适合用来进行基坑沉降预测。
(2)从模型解算方法来看,宜采用总体最小二乘来解算灰色模型中的灰参数。
(3)文中只采用了灰色模型进行建模预测分析,而除了灰色模型外,还有时间序列模型、回归分析法等可以用来进行建模预测,后续的工作可以将其他模型与基于总体最小二乘的新陈代谢灰色预测模型进行对比研究,得出更适合基坑沉降的预测模型。
(4)充分挖掘各种预测模型的优势,在不同的预测阶段采用优势模型来预测,以使预测结果更加可靠。
(5)后续研究可从数据处理方法和新模型的构建着手,如对数据进行预处理后再建模、挖掘新的模型解算方法、挖掘建立新的更加符合实际的预测模型。

