偏振光学成像：器件，技术与应用（特邀）

任立勇，梁健，屈恩世，张文飞，4，杜博军，马菲雅，郭少犇，张进

（1 陕西师范大学 物理学与信息技术学院，西安710119）

（2 中国科学院西安光学精密机械研究所，西安710119）

（3 西安市光信息调控与增强技术重点实验室，西安710119）

（4 山东理工大学 物理与光电工程学院，山东 淄博255000）

（5 中国人民解放军63861 部队，吉林 白城137001）

0 引言

一直以来，光学成像技术在人类感知和记录客观世界事物中发挥着巨大的作用。光波是一种电磁波，对光波四个基本参量的利用分别对应一种光学成像方式或方法，同时光学成像技术的发展历程也反映着人类感知或记录光的能力及技术手段的不断进步。记录光的振幅信息对应强度成像方式，获得了目标的黑白照片；记录光的波长（或频率）信息对应光谱成像方式，获得了目标的彩色照片；记录光的相位信息对应全息成像方式，获得了目标的全息照片；人眼固有的偏振不敏感性，使得作为光的四个基本属性之一的偏振成为了被人类发现和利用最晚的一个光波属性。即便如此，基于对光的偏振信息探测的偏振光学成像技术，已经成为了现代光学成像技术的前沿研究热点。

众所周知，偏振是光波电场振动方向对光传播方向的不对称性，是横波区别于纵波的重要标志，是光的一个重要的信息维度。事实上，光波的偏振特性包含着丰富而独特的信息，往往是光的其他属性所不具备的。物体反射光或辐射光的偏振特性（一般用光的偏振度和偏振角这两个参量来描述）与其材质、几何形状、纹理结构、表面粗糙度、理化特性等本身性质密切相关。不同类型的目标，即使他们具有相同的强度反射率，其反射光的偏振特性也往往表现出较大差异。而决定目标反射光偏振特性的因素很难被伪装和隐藏，因此通过对目标反射光的偏振特性测量可以有效地探测和凸显复杂背景下的感兴趣目标。作为对传统的强度成像、光谱成像和红外辐射成像等成像方式的有效补充手段，偏振光学成像这种新型的光学成像技术，为低信噪比复杂背景环境、强散射环境、低照度环境下的目标成像探测等，提供了创新的技术手段。

自从HUYGENS C 研究光波在晶体中传播时发现了光的偏振特性之后，对光的偏振信息获取和处理技术的研究一直是该领域的热点。1852年，STOKES G 提出了一种将光的偏振特性反映到其强度上的探测方法，使得人们对光偏振信息的观察和获取变得更加直观而方便。自此，斯托克斯（Stokes）矢量被广泛应用到偏振光学成像探测技术中，极大地促进了该技术的发展。2000年，美国Physics Innovations Inc.和Lockheed Martin Corp.联合开展了长波红外偏振光学成像研究［1］，结果表明在目标与背景热辐射强度相近时，通过偏振光学成像技术可有效地增强军事目标的对比度，提升目标的识别概率。2003年，瑞典国防研究局利用长波红外偏振光学成像技术对隐藏在军用网后的军事目标进行了偏振光学成像研究［2］，结果表明偏振光学成像技术对隐藏目标的探测能力比强度光学成像技术更强。2004年，美国空军研究实验室对战斗机表面涂层的偏振特性进行了深入研究［3］，并与植被目标偏振特性进行了对比，结果表明偏振光学成像技术对伪装目标的强探测能力。2005年，以色列ELOP 公司提出了一种长波红外偏振光学成像探测方法［4］，展现了偏振光学成像技术相对于强度成像可有效提升复杂背景环境中目标的探测能力。同年，美国Polaris Sensor Technologies 公司在实验上发现了长波红外偏振光学成像技术可被有效地应用于海面目标的探测［5］。2011年，加拿大国防研究及发展中心以机械转轮控制偏振片转动，实现了0.4～0.9 μm 的可见光波段、1.0～1.9 μm 的近红外波段、3～5 μm 的中波红外波段和8～12 μm 长波红外波段的多波段偏振光学成像［6］，展示了偏振光学成像技术在探测隐藏和伪装的人造军事目标时的独特优势。早期阶段，红外偏振探测理论、红外偏振光学成像系统及其探测应用，在军事和民用领域引起了广泛关注。例如，在红外伪装涂层下隐身目标的探测和识别应用需求中，红外偏振光学成像发挥了重要作用，它能有效抑制背景杂波，提高目标与背景的对比度，增强目标物的信息量和成像探测距离，提高热像仪对温差小或热对比度低的目标的探测识别能力［7-8］。近年来，随着纳米加工能力的提升，基于日本Sony 公司生产的微偏振片阵列图像芯片促进了可见光偏振光学成像技术的快速发展，典型代表是美国FLIR 公司和Lucid 公司推出的分焦平面偏振相机。

偏振光学成像技术的发展及其成像探测应用需求，极大地促进了偏振光学成像系统（相机）的研制。偏振光学成像系统可分为分时和同时偏振光学成像系统两大类。分时偏振光学成像系统通过旋转相机镜头前的线偏振片，依次获得0°、45°、90°和135°线偏振方向的强度图像，最后计算获得线偏振度图像或偏振角图像。分时偏振光学成像系统具有简单易实现的优势，但存在旋转角度精度低、偏振探测能力差、不适合对运动目标成像等缺陷。同时偏振光学成像系统又分为分振幅型［9-10］、分孔径型［11-12］和分焦平面型［13-14］。分振幅型偏振光学成像系统借助分光棱镜分光和各支路偏振调制方案，可实现多探测器或单探测器共享的偏振光学成像。2011年，美国洛克希德马丁公司采用棱镜二次反射的方法将四路光调整至一个方向，实现了单探测器分振幅型偏振光学成像。该成像系统结构紧凑，可靠性高，但由于四路光反射次数不同，需根据每一路自身的特性补偿光程差和像差，设计相对复杂；分孔径型偏振光学成像系统在前端光学镜头的孔径光阑处并行放置多个不同的偏振调制元件，在后端聚焦时采用聚焦透镜组实现多通道分别聚焦，从而在单一探测器的不同象限上获得目标的不同偏振态图像，由于四个通道的装配误差必然会导致四幅偏振子图像之间存在位置偏差，因此，分孔径偏振子图像间的配准尤为重要；分焦平面型偏振光学成像系统将偏振片的尺寸制作到微米量级，再将不同方向的微偏振片组成阵列并放置于探测器前，探测器每一个感光像元与一个方向的微偏振片对应。高质量金属线栅微偏振片阵列图像芯片的研制成功，极大地促进了分焦平面偏振相机及偏振光学成像技术的推广应用。

大量研究表明，基于目标反射光和背景杂散光的偏振特性差异，偏振光学成像技术在改善目标成像质量、提高作用距离、提升探测能力和增强识别概率等方面具有重要的意义，在工业检测［15-16］、生物医学［17］、光学遥感和地球物理［18］、大气科学及云层探测［19］、水下勘探和开发［20］、军事目标探测和识别［5］等领域具有重要的应用价值。特别是在物体识别与分割［21］、材料及表面缺陷检测［22］、动态干涉计量［23］、生物组织病变诊断［24］、目标探测与对比度增强［25］、镜面强反射去除［26］、3D 轮廓信息提取［27］、透明固体材料内应力测量［28］、去雾去散射清晰成像［29-42］、复杂环境（如海洋、沙漠）中不易发现的移动目标［43］和暗弱目标［44］的快速侦察和探测等方面表现出了诸多独特优势。

国内在偏振光学成像探测技术及偏振相机研制方面开展了诸多研究工作。中国科学院上海技术物理研究所［45］成功研制了亚波长金属线栅微偏振片阵列的近红外InGaAs 偏振探测器；合肥新星应用技术研究所［46］在偏振光学成像技术探测人造目标方面进行了深入研究；南京理工大学［25］在自适应目标增强偏振光学成像技术方面做出了贡献；天津大学［47-48］在水下偏振去散射图像恢复及增强成像方面进行了系统的研究；西北工业大学［49］研制了8～12 μm 波段的非制冷型分焦平面红外偏振相机。此外，北京理工大学、北京航空航天大学、南京航空航天大学、中北大学、东北师范大学、国防科技大学、中国人民解放军陆军军官学院、中国科学院西安光学精密机械研究所、西安交通大学、西安电子科技大学等单位都在积极参与该领域的研究工作。

2012年以来，本研究团队在中国科学院西安光学精密机械研究所开展偏振相机研制及偏振光学成像探测技术研究［12，14，29-42，50-58］。2015年，研制出了一款三个线偏振和一个圆偏振同时探测的分孔径型彩色全偏振态相机［12，50］。本文对偏振光学成像探测方面的研究工作及成果进行了较为详细的介绍和总结，并对偏振光学成像研究目前需要解决的技术问题和发展方向给出了思考和建议。仅以此文纪念中国科学院西安光学精密机械研究所建所60 周年。

1 偏振光学成像理论

1.1 偏振光的Stoke 矩阵表示

通常情况下，沿z轴方向传播的光，其光波电场可表示为沿x轴（水平轴）和y轴（垂直轴）方向正交振动的两个光波的合成。对于给定频率的振动，两个分振动是确定的且保持一定的相对关系，其合成光波电场的电矢量端点将描绘出三维的轨迹。相互正交的两个振动分量可表示为

式中，ω和λ分别为光波的角频率和波长，E0x和E0y分别为x和y方向的振幅，φx和φy分别为x和y方向的初始相位。定义φ=φx-φy为x和y方向之间的初始相位差。由于两个光波分量都在z方向传播，其合成的光波电场E（z，t）满足光矢量方程

当φ为常量时，式（2）表示一个椭圆方程，表明光矢量通常是椭圆偏振的；特别地，当φ是π 的整数倍时，光矢量变为线偏振的；当E0x=E0y，φ=±π/2 时，光矢量变为圆偏振的；当φ为随机数时，光矢量为非偏振的。当光波中既包含非偏振光，又包含偏振光，称为部分偏振光。

1852年，STOKES G 在研究部分偏振光时，为便于表征和测量光的偏振态，引进了Stokes 矩阵，即

式中，I0、I45、I90和I135分别表示光波中0°、45°、90°和135°的线偏振成分的光强，IR和IL分别表示光波中右旋圆偏振和左旋圆偏振成分的光强；S0表示光波的总强度，S1表示水平（0°）和竖直（90°）方向上线偏振光的强度差，S2表示45°和135°方向上线偏振光的强度差，S3表示右旋与左旋圆偏振光的强度差。T 表示矩阵转置操作。可见，Stokes 矩阵是一个4×1 的列矩阵，S1和S2描述光波的线偏振部分，S3描述光波的圆偏振部分。

1.2 偏振光学成像的基本原理

在实际应用中，通过拍摄同一场景目标的多幅不同偏振态（例如：0°、45°、90°和135°线偏振、右旋圆偏振、左旋圆偏振）下的强度图像，可获得Stokes 矩阵参量，即

根据式（5），可得到描述光波偏振特征的三个基本参数：偏振度、偏振方位角和偏振椭偏角。

1）偏振度（Degree of Polarization，DoP）：表示完全偏振光强度在整个光强度中所占的比例，表示为

DoP 的取值范围为［0，1］，其中，0 表示光波为完全非偏振光（即自然光）；1 表示光波为完全偏振光；其他值表示光波为部分偏振光。

2）偏振方位角（Angle of Polarization，AoP）：表示偏振光电矢量主振动方向与参考方向（通常取水平方向x 轴）的夹角，表示为

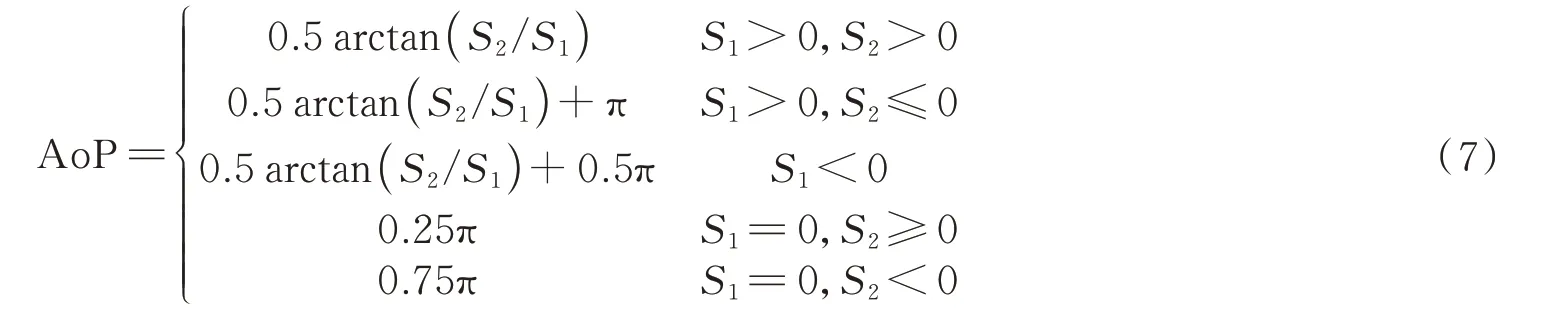
AoP 的取值范围为［0，π］rad，式（7）表明，AoP 的大小依赖于S1和S2的大小和符号。

3）偏振椭偏角（Ellipticity Angle of Polarization，EoP）：反映椭圆短轴与长轴之比，表示为

EoP 的取值范围为［-π/4，π/4］rad，其中，EoP=0 代表线偏振光，EoP=-π/4 和EoP=π/4 分别代表左旋圆偏振光和右旋圆偏振光。

根据以上偏振特征参数，可以获得场景目标的偏振度图像、偏振角图像和偏振椭偏角图像，用于偏振光学成像及目标偏振探测和识别。

2 分孔径偏振光学成像系统的设计、关键器件及技术

从偏振光学成像基本理论可知，为了获得目标的全偏振态信息，如式（5）所示，需要同时获得目标的0°、45°、90°三个线偏振光强信息（即I0、I45和I90）和一个右旋圆偏振光强信息（即IR）。为此，采用分孔径偏振光学成像系统，在孔径光阑处并行放置0°、45°、90°三个线偏振片和一个右旋圆偏振片实现全偏振态提取，并通过四个通道分别聚焦成像及共用同一个探测器，可实现分孔径全偏振态同时成像。

与其他偏振光学成像系统相比，分孔径偏振光学成像系统有独特的优势，其结构紧凑，实时性强，能够同时获取场景的全偏振态信息，适合对动态目标进行全Stoke 矢量的偏振光学成像探测及应用研究。本节结合研究团队在分孔径全偏振态成像相机整机及分孔径全偏振态成像镜头方面的研究工作，主要介绍分孔径偏振光学成像系统的设计、关键器件及技术。

2.1 分孔径全偏振态同时探测型彩色偏振相机

从目前市面上偏振相机产品来看，凡是全偏振态探测的都是分时型偏振光学成像模式，而凡是同时型偏振光学成像模式的都只能探测线偏振光成分，缺乏对圆偏振光成分的探测。另外，偏振相机目前没有国产品牌，使用最多的是美国FLIR 公司和Lucid 公司生产的分焦平面型偏振相机，其芯片均采用日本Sony 公司的金属线栅微偏振片阵列，因此不能探测圆偏振光成分。

图1 所示为研究团队在中国科学院西安光学精密机械研究所研制开发的分孔径全偏振态同时探测型彩色偏振相机［12］，相机采用分孔径共焦面多幅成像的光学设计，结构紧凑、通光量高；机械结构多采用一次成型工艺，具有精度高的优点；电子学部分采用FPGA 乒乓结构缓存与运算，可对大数据图像进行高速处理，能够满足25 帧/s 的视频流输出，输出端采用逐行倒相（Phase Alteration Line，PAL）制式模拟信号和千兆网数字信号同时输出，增强了偏振相机实时探测和后期分析处理能力。图1（a）为成像焦面处三个线偏振和一个右旋圆偏振的排布示意图；图1（b）为偏振相机实物图。

图1 分孔径全偏振态同时探测型彩色偏振相机［12］Fig.1 Division-of-aperture chromatic polarimetric camera with full-polarization-state simultaneous detection［12］

该分孔径偏振光学成像相机的光学总体方案设计包括前端望远镜系统和后端分光与传光系统。前端采用2 倍无焦放大系统，有利于配合后端的孔径分光结构和提高整个光路的角分辨率；后端采用四路对称的孔径分光方案，有利于合理分配光能和减少因路径不同导致的像质畸变。目标反射光经由望远镜系统后平行入射到分光系统，并被四个斜方棱镜平均分成四束光；在四通道的棱镜前分别摆放偏振方向为0°、45°、90°的线偏振片以及右旋圆偏振片，实现对四束光偏振信息的有效提取；经过偏振提取后的光经聚焦系统和斜方棱镜后聚焦到同一个探测器靶面的不同区域上，完成对目标四路不同偏振信息的获取。图2 为该相机样机光学系统的光路模拟图，偏振片左边部分为前端望远镜系统，右边为后端分光与传光系统。图3 为后端分光与传光系统的三维结构示意图。

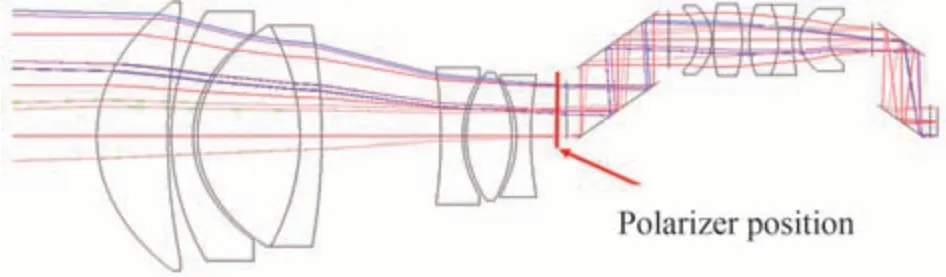
图2 偏振相机光学系统光路模拟图［50］Fig.2 Optical-path simulation diagram of optical system of polarimetric camera［50］

图3 分光与传光系统三维结构示意图Fig.3 Schematic diagram of three-dimensional structure of light separation and transmission system

该偏振相机的主要技术指标包括：1）波段为400～700 nm；2）帧频为25 帧/s；3）焦距为76 mm；4）视场为4.2°×4.2°；5）输出图像大小为1 024×768；6）角分辨率为0.073 mrad；7）偏振探测精确度≥95%。

2.2 分孔径全偏振态同时成像镜头

为满足偏振光学成像探测的实际应用要求，将普通相机镜头拿掉，更换成专门设计的全偏振态同时探测的分孔径偏振光学成像镜头，是实现偏振光学成像和研制偏振相机的一种便捷技术方案。这种全新的设计思路架构，最大限度地借助和利用了普通商用相机的已有硬件物理基础，把工作重心放到了镜头研制和软件算法设计这两部分，其中，镜头研制主要包括基于分孔径技术的四种偏振态同时探测的偏振光学成像镜头的设计、加工、装配；软件算法设计主要完成图像配准、偏振定标、偏振光学成像去散射图像分析与增强处理算法。

图4 所示为团队研制的分孔径全偏振态同时成像镜头的实物图和点阵目标靶及其偏振光学成像输出。该镜头用于将7 500 帧/s 高速摄像机改制成偏振摄像机，实现了低照度条件或烟雾等低密度介质干扰下高速摄像像质改进与图像信息恢复的应用需求，为提升尾焰、爆炸光、烟雾等影响下成像系统的测量能力，拓展系统作用距离和提高系统成像质量，开展高速飞行目标的偏振特性研究、定量化测试和直观显示提供了技术手段和关键装备。

图4 研制的分孔径全偏振态同时成像镜头Fig.4 Developed division-of-aperture polarimetric lens with full-polarization-state simultaneous detection

该分孔径全偏振态同时成像镜头的主要技术指标包括：1）工作距离为50～1 000 m；2）波段范围为450～650 nm；3）焦距为100 mm（±1%）；4）相对孔径（D/f）为1∶2.5（分孔径前的瞳孔直径/组合焦距）；5）空间分辨率≤0.5 mrad。

2.3 分孔径偏振相机的图像配准技术

在实际应用中，分孔径偏振相机四个通道的装配误差不可避免地会导致四幅偏振子图像之间存在位置偏差。而计算物体的偏振信息需要准确获取同一物点在探测器靶面四个像点的强度信息，因此，分孔径偏振相机的图像配准技术尤为重要。

建立了分孔径偏振相机的图像配准方法，其主要处理步骤包括：基于相位相关算法［59］实现偏振子图像间的粗配准；基于加速稳健特征（Speeded-up Robust Features，SURF）算法［60］实现偏振子图像的特征点提取与配对；以及基于随机采样一致性（RANdom SAmple Consensus，RANSAC）算法［61］实现偏振子图像间的精细配准。按照实现步骤对该配准技术进行介绍，最后给出图像配准的实验效果及量化评价分析。

1）基于相位相关算法实现偏振子图像的粗配准

首先，将分孔径偏振相机所拍摄的目标原始帧图像裁切为四幅偏振子图像，选取其中任意一幅偏振子图像为参考偏振子图像，其余三幅偏振子图像为待配准偏振子图像；其次，采用相位相关算法通过快速傅里叶变换将参考偏振子图像f（x，y）和待配准偏振子图像g（x，y）从空域变换为频域偏振子图像F（ωx，ωy）和G（ωx，ωy），然后通过计算两幅频域偏振子图像的互功率谱来得到两幅空域偏振子图像的平移量关系，即

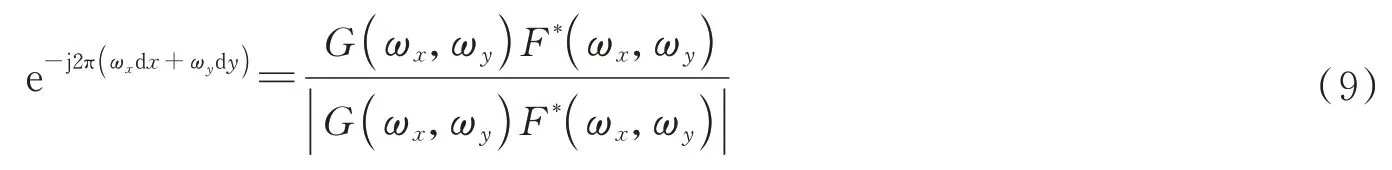
式中，dx和dy为待配准偏振子图像相对于参考偏振子图像在水平和垂直方向的位移量，*表示取复共轭。对

式（9）两边分别进行傅立叶反变换，左侧得到冲击函数δ(x-dx，y-dy)，右侧得到冲击函数的峰值位置，即两幅图像f(x，y)与g(x，y)在水平和垂直方向的平移量dx和dy。

采用上述相位相关算法，分别获得三幅待配准偏振子图像与0°线偏振子图像（参考偏振子图像）的位置平移量，即得到粗配准后的45°线偏振子图像、90°线偏振子图像和右旋圆偏振子图像。

2）基于SURF 算法提取偏振子图像的特征点并实现特征点的配对

SURF 算法［60］是一种具有鲁棒性的局部特征点检测与描述的算法，其运行速率快，准确度高，重复性强。对参考偏振子图像与粗配准后的偏振子图像分别进行特征点提取，得到两幅偏振子图像的多个特征点。对于参考偏振子图像中的任意一个特征点，在粗配准后的偏振子图像中选择与其欧式距离最近邻和次近邻的两个特征点，当最近邻距离与次近邻距离的比值不大于所设置的阈值（通常选为0.7）条件时，则认为参考偏振子图像中的特征点与粗配准后的偏振子图像中欧式距离最近邻的特征点匹配成功，形成一个特征点对，由匹配成功的所有特征点对构成特征点对集合。

通过SURF 算法分别提取0°线偏振子图像（参考偏振子图像）与粗配准后的45°线偏振子图像、90°线偏振子图像和右旋圆偏振子图像间的特征点，并形成三组特征点对集合。

3）基于RANSAC 算法优化偏振子图像间的配准参数

RANSAC 算法是由FISCHLER M A 与BOLLES R C 于1981年提出，它是一种高鲁棒性的数据拟合算法［61］，其在完成聚类的同时，可以得到对应模型的最优参数。

设经SURF 算法特征点匹配后参考偏振子图像与粗配准后的偏振子图像所构成的特征点对集合包含M个特征点对，参考偏振子图像中任意特征点的坐标为（x′，y′），粗配准后偏振子图像中与之对应的特征点的坐标为（x，y），二者之间的仿射变换关系可表示为

式中，A为仿射变换矩阵。从参考偏振子图像与粗配准后偏振子图像的特征点对集合中随机选取三个特征点对，由式（10）可计算出所选的三个特征点对所确定的仿射变换矩阵A，然后利用矩阵A计算出粗配准后偏振子图像的其余M-3 个特征点的变换坐标，并与参考偏振子图像中与之对应的特征点的坐标进行比较，将所计算出的坐标满足式（11）条件的特征点记作内点。

式中，角标n可取45、90 和C，分别对应45°线偏振、90°线偏振和右旋圆偏振，为粗配准后偏振子图像特征点通过仿射变换矩阵A所计算得到的坐标为与粗配准后偏振子图像特征点相对应的0°线偏振子图像（参考偏振子图像）特征点的坐标。统计内点数目，选取内点数目最多的仿射变换矩阵A作为配准系数，分别完成三幅粗配准后的偏振子图像与参考偏振子图像的精细配准操作。由此确定的三个仿射变换矩阵，将作为相应的分孔径偏振相机的固有配准参数。

采用上述图像配准方法，对图1 分孔径全偏振态同时探测型彩色偏振相机进行图像配准，并给出实验结果和配准效果量化评价。图5 给出了分孔径偏振相机采集的一帧原始图像，同时标出了四幅偏振子图像的分布。图6 给出了四幅偏振子图像的配准结果。

图5 分孔径偏振相机的一帧原始图像Fig.5 A frame of raw image from division-of-aperture polarimetric camera

图6 偏振子图像配准结果Fig.6 Registered results of polarized images

分别采用结构相似性指数（Structural Similarity，SSIM）［62］及归一化互信息（Normalized Mutual Information，NMI）［63］对所配准的偏振子图像进行了量化评价，以分析偏振子图像的配准效果。其中，SSIM 从图像组成的角度来描述场景中物体结构的属性，它将图像结构信息定义为独立于图像亮度和图像对比度之外的第三个信息维度，采用图像灰度均值作为其亮度的估计，图像灰度标准差作为其对比度的估计，图像灰度协方差作为其结构相似程度的估计，将图像间的失真建模并描述为亮度、对比度和结构三个不同因素的组合。SSIM 的取值范围为［0，1］，取值越大代表两幅图像的相似程度越高。NMI作为度量两幅图像相似度的一个标准，通常用作图像配准中的评判准则或目标函数，取值范围为［0，2］，取值越大代表两幅图像的相似性越高。

为了定量化分析图像配准效果，分别计算了图像配准前后两种情形下偏振子图像两两组合时的结构相似性指数（SSIM）和归一化互信息（NMI），结果分别如表1 和表2 所示。

表1 图5 和图6 偏振子图像两两组合时的结构相似性指数Table 1 SSIM of every two polarized images of scene shown in Fig.5 and Fig.6

表2 图5 和图6 偏振子图像两两组合时的归一化互信息Table 2 NMI of every two polarized images of scene shown in Fig.5 and Fig.6

从表1 和2 可以看出，配准后的四幅偏振子图像相比于未配准的四幅偏振子图像，其SSIM 和NMI 均有了较大提升。其中，SSIM 平均提升了72.08%，NMI 平均提升了18.5%，表明所提出的分孔径偏振相机偏振图像配准方法具有很好的可行性。

对于同一场景目标，分别基于配准前和配准后的偏振子图像计算了其偏振度（DoP）图像和偏振角（AoP）图像，结果如图7 所示。

图7 配准前后的偏振子图像计算得到的偏振度图像和偏振角图像Fig.7 DoP image and AoP image calculated from polarized images before and after registration

对比基于配准前后的四幅偏振子图像分别计算所得到的场景目标的DoP 图像和AoP 图像，可以发现配准后计算所得到的场景目标的DoP 图像与AoP 图像没有明显重影，图像质量更高，能够较好地突出场景目标的细节信息，进一步说明了分孔径偏振相机配准工作的重要性以及配准方法的可行性。

2.4 偏振-颜色编码滤波的光瞳分光型同时偏振光学成像系统

与传统的分时、分振幅［9-10］、分孔径［11-12］和分焦平面［13］的偏振光学成像方法相比，我们提出了基于偏振-颜色编码滤波的光瞳分光型同时偏振光学成像方法［14，51］，可大幅降低光学系统设计的复杂性，有利于偏振相机的小型化和集成化，且能保留原相机系统的成像分辨率。

2.4.1 光瞳分光型同时偏振光学成像方法的基本原理

基于偏振-颜色编码滤波的光瞳分光型同时偏振光学成像方法的基本原理体现在其实现方案的三个步骤：1）将特殊设计的偏振-颜色滤波片放置在成像镜头的光瞳位置处，该偏振-颜色滤波片包含3个颜色通道，每一个颜色通道对应一个方向的偏振片；2）利用普通彩色相机和装有偏振-颜色滤波片的成像镜头对目标场景成像，经过调制的入射光在像面上非相干叠加，同时在整个光学探测器上成像；3）利用彩色相机拜尔滤镜特性，基于红绿蓝（RGB）三通道图像解算出场景的偏振图像，最终实现同时偏振光学成像功能。

偏振-颜色滤波片是该方法的核心元件［64］，其结构如图8 所示。偏振-颜色滤波片由两部分组成，分别是颜色滤波片和偏振片。每个部分又等分为三片，颜色滤波片分为红色R、绿色G 和蓝色B，偏振片分为0°、60°和120°的三个线偏振部分。颜色滤波片和偏振片一一对应，即红色滤波片R 调制0°线偏振光，绿色滤波片G调制60°线偏振光，蓝色滤波片B 调制120°线偏振光。

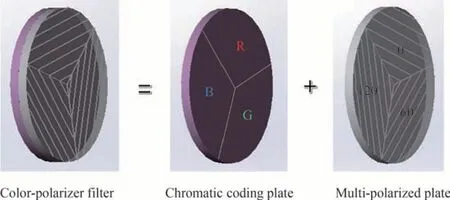
图8 偏振-颜色滤波片结构示意图Fig.8 Structure diagram of polarization-color filter

偏振光学成像系统的光路示意图如图9 所示。通过偏振-颜色滤波片后的三个出射光分别表示为

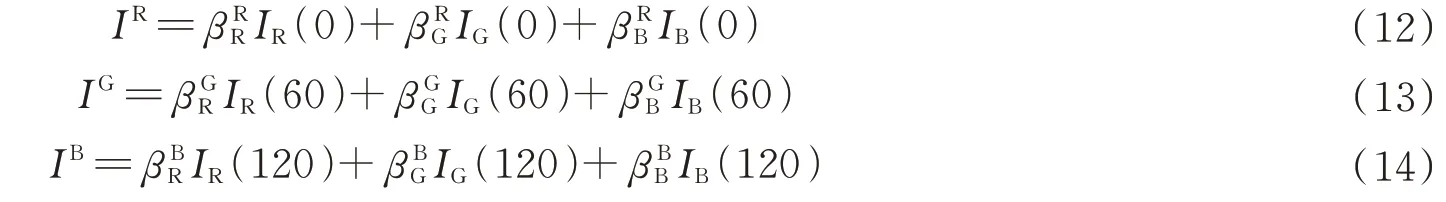
图9 偏振-颜色编码滤波的光瞳分光型同时偏振光学成像的光路示意图Fig.9 Schematic of optical path of division-of-aperture simultaneous polarimetric optical imaging based on color-polarizer filter

式中，β表示颜色滤波片透过率，下角标R、G、B 分别表示入射光中的红、绿、蓝成分，0、60 和120 分别表示线偏振片的透振方向，探测器获得不同颜色通道的图像是上述三个出射光的非相干叠加，即

偏振光学成像应用通常可忽略目标偏振态对波长的依赖关系［65-66］。因此，可认为在红绿蓝三个波段上目标反射光的偏振态是一致的，于是式（15）～（17）可表示为矩阵形式，即

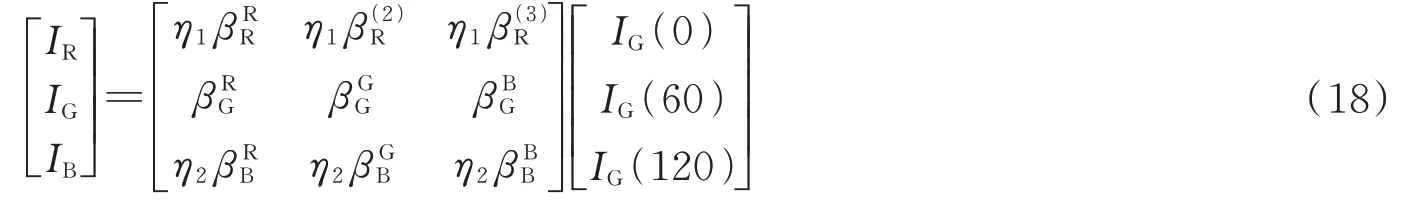
式中，η1为红光与绿光的强度比，η2为蓝光与绿光的强度比，通过式（18）可以解算出IG（0）、IG（60）和IG（120）三幅偏振子图像。进而根据三幅偏振子图像，获得场景反射光的Stokes 矢量

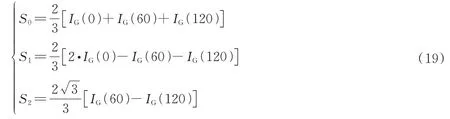
2.4.2 光瞳分光型同时偏振光学成像系统性能测试

与采用分焦平面偏振器阵列的商用彩色偏振相机相比，该偏振光学成像系统具有更高的空间分辨率。在彩色偏振相机中，每个像素只能感知一种颜色的一种偏振状态，意味着需要4×4 个像素才能获得单个物点的颜色和偏振特性。然而，在基于偏振-颜色编码滤波的光瞳分光型同时偏振光学成像方法中，空间分辨率与常规彩色相机的空间分辨率相同，意味着该系统空间分辨率是彩色偏振相机的两倍。

图10（a）和（b）分别是偏振-颜色编码滤波的光瞳分光型同时偏振光学成像方法和商用彩色偏振相机对美国空军分辨率板拍摄的红色通道的0°线偏振图像。图10（c）和（d）显示的是图10（a）和（b）中红线和蓝线的轮廓图。从图中可以看出，光瞳分光型同时偏振光学成像方法可以分辨第3 组中的元素3（即E3G3），而商用彩色偏振相机只能分辨第2 组中的元素4（即E4G2），空间分辨率是商用彩色偏振相机的1.78 倍。

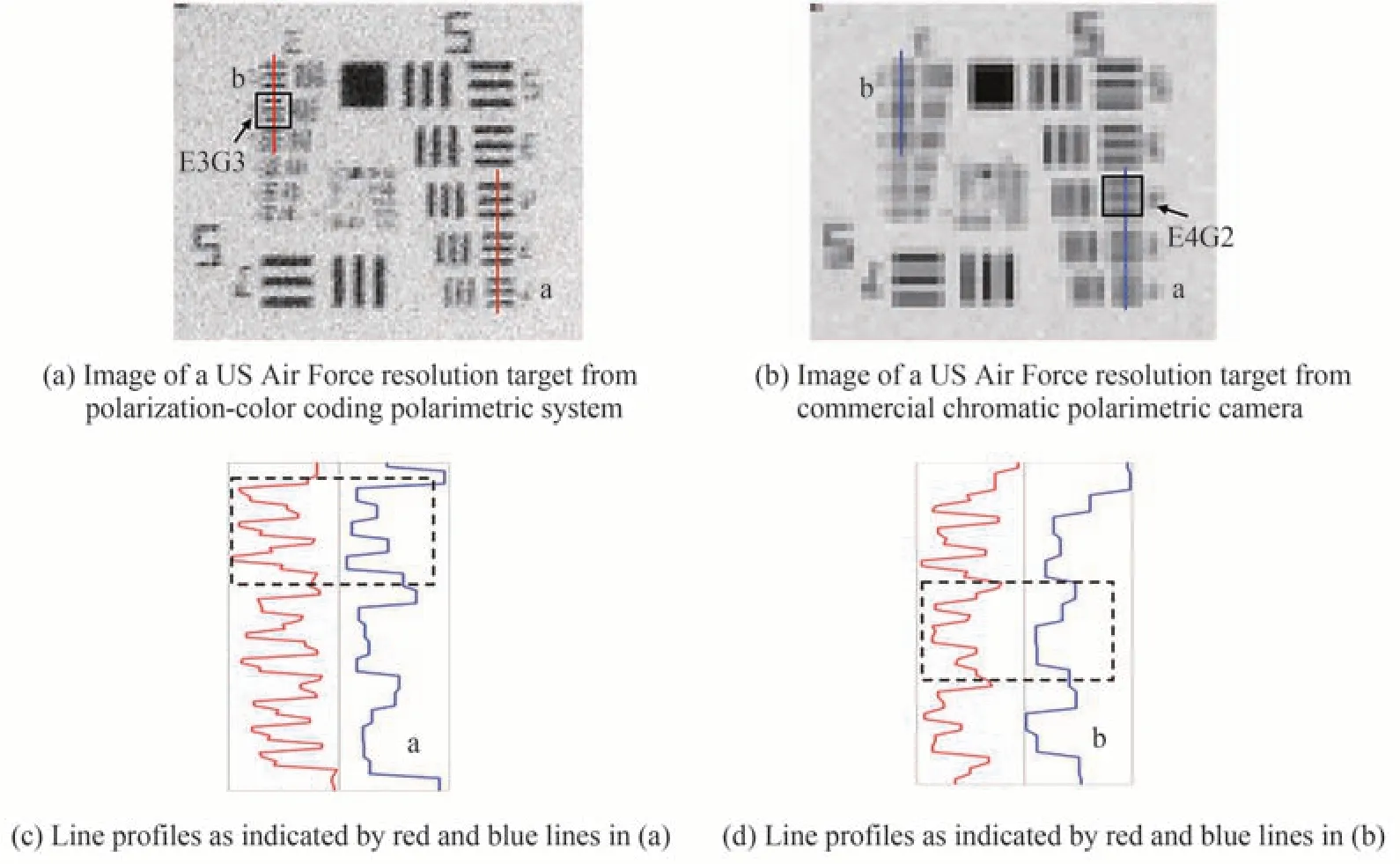
图10 空间分辨率对比［14］Fig.10 Comparison of spatial resolution［14］

此外，对该方法的偏振探测精度进行了定量化分析［51］。如图11 所示，设计并制作了一个多角度线偏振片探测目标，其中，图11（a）为制作的多角度线偏振片实物，图11（b）为偏振片的线偏振方向示意图，图11（c）为该方法的直接拍摄图。采用分时偏振光学成像方法，得到图11（a）所示探测目标的偏振度图像为图12（a）、偏振角图像为图13（a）。对于偏振-颜色编码滤波的光瞳分光型同时偏振光学成像方法，将图11（c）目标图像中的红绿蓝颜色通道分离出来，利用式（18）计算出0°、60°和120°的线偏振子图像，进而获得偏振度图像和偏振角图像分别如图12（b）和图13（b）所示，偏振度测量的平均误差为3.9%，偏振角测量的平均误差为3°。

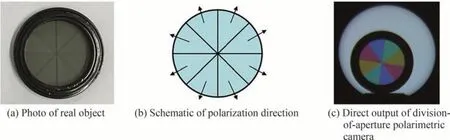
图11 多角度线偏振片Fig.11 Multiangle linear polarizer

图12 偏振度图像对比Fig.12 Comparison between DoP images

图13 偏振角图像对比Fig.13 Comparison between AoP images

2.4.3 光瞳分光型同时偏振光学成像方法优点

偏振-颜色滤波片在孔径光阑位置处进行光波编码调制，成像分辨率相对于商用彩色偏振相机提升了2 倍。偏振-颜色滤波片设计更加灵活，可实现对目标的圆偏振和椭圆偏振成分的探测。单光路保证了多幅子图像间的像素级配准，不存在图像畸变。成像系统结构紧凑，成本低，方便移植和升级改造。

3 偏振图像信息处理技术、算法及成像应用

从学科类别来看，偏振光学成像属于近年来快速发展的热点学科-计算光学成像。除了基于偏振光学成像系统的偏振信息获取方法和技术之外，偏振光学成像研究很重要的另外一部分工作是偏振图像信息处理。因此，本节将介绍研究团队在偏振图像信息处理的技术、算法及成像应用方面开展的一些研究工作，主要包括偏振去雾/去散射成像、可见光/近红外偏振图像融合成像、偏振三维（3D）重构成像。

3.1 偏振去雾/去散射成像

在烟雾霾等气象环境中，图像的能见度和成像对比度降低，成像质量下降，对观察目标和进一步图像处理产生了诸多影响。同时，随着科技的发展，无人机、自动驾驶和卫星遥感等应用对图像的依赖越来越强，对图像质量的要求也越来越高，因此，去雾/去散射成像技术受到了广泛关注。根据处理方式的不同，去雾/去散射成像技术主要可分为图像处理去雾/去散射技术和光学去雾/去散射技术。

图像处理去雾/去散射技术主要针对单幅雾霾图像，可分为图像增强技术和图像复原技术［29］。图像增强技术通常不考虑成像环境的影响，利用图像处理的方法直接增强图像对比度，例如直方图均衡化技术［67］和Retinex［68］技术等。该技术的优点在于计算速度快、对应用环境没有限制；缺点是稳定性不高、噪声抑制能力弱。图像复原技术主要通过物理退化模型来估算图像退化参量，利用该参量进行图像复原［69-71］。该技术的优点在于复原图像保真度高、细节还原能力强；缺点是算法复杂度高、适用范围有限。

光学去雾/去散射技术通过对成像系统的改造可获得同一场景的多幅雾霾图像，再利用物理退化模型进行图像处理和融合重构出该场景的复原图像，主要包括光谱融合技术［72］和偏振光学成像技术［73］。该技术虽存在获取图像方式较复杂的不足，但是具有算法简单、普适性好、图像保真度高等优点。偏振光学成像去雾/去散射技术近年来得到了广泛关注，一些新型的技术和方法相继被提出［12，30］，其应用环境也从雾霾逐渐扩展到水下、生物组织等散射介质中［74］。

3.1.1 基于偏振角参量估算的偏振光学成像去雾/去散射方法

偏振光学成像去雾方法的物理退化模型［75］如图14 所示。可以看出，到达相机镜头的光分为两部分：一部分是目标反射光经过雾霾颗粒散射和吸收后到达探测器的光，称为直接透射光（即信号光）；另一部分是太阳光直接经雾霾颗粒散射后到达探测器的杂散光，称为大气光（即噪声光）。

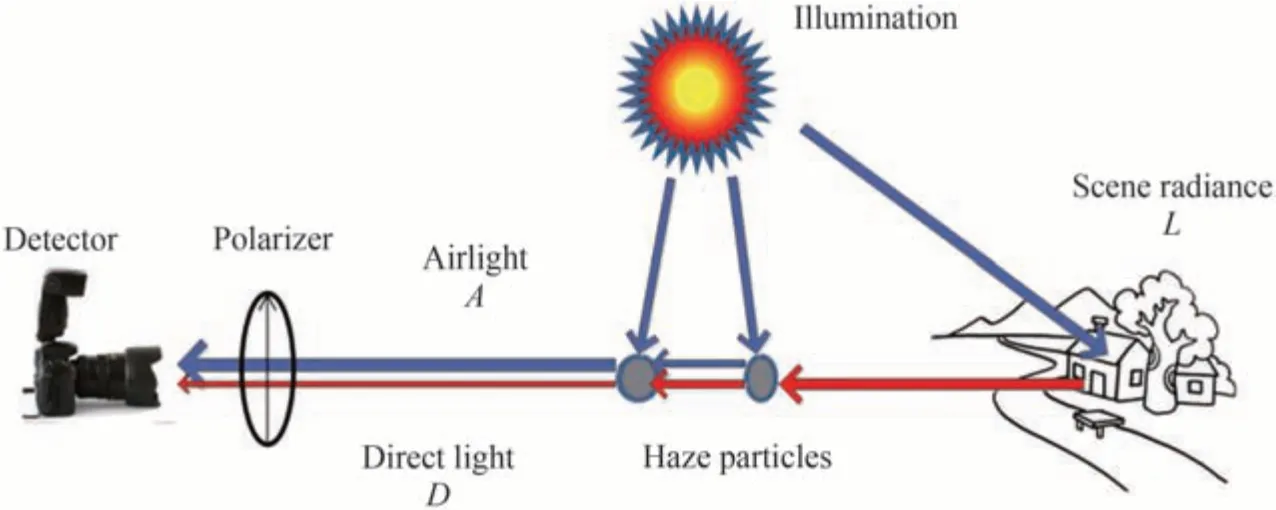
图14 散射环境中的物理退化模型示意图［75］Fig.14 Schematic of physical degradation model in scattering environment［75］

大气光强A可以表示为

式中，A∞表示无穷远处的大气光强，t（z）表示传输系数，z表示传输距离。t（z）可表示为

式中，β表示衰减系数，主要为吸收和散射效应造成的光能量损耗。该模型中，假设β与z无关，即假设散射介质是均匀稳定的。因此，式（21）可改写为

根据式（22），当z→∞时，t→0，则式（20）中，A=A∞。即无穷远处大气光强是大气光强的一种特殊情况，

可以理解为当目标处于无穷远处时，到达探测器的光强。

直接透射光强D可以表示为

式中，L是衰减前的目标反射光强，即去雾后需要恢复的目标处反射光强。相机探测到的总光强I是大气光强和直接透射光强的非相干叠加，即

结合式（20）、（23）和（24），可获得L的表达式为

从式（25）中可以看出，物理退化模型的两个关键参数分别是大气光强（A）和无穷远处大气光强（A∞）。研究表明，大气光和直接透射光的偏振特性存在显著差异，因此，通过偏振光学成像技术可以有效分离大气光和直接透射光，估算出式（25）的两个关键参数，从而实现去雾/去散射成像。

基于偏振角参量估算的偏振光学成像去雾/去散射方法主要分为以下四步［31］：

1）确定大气光的偏振角特征参量和偏振度特征参量。通过偏振光学成像方法，可以获取同一场景的不同偏振图像，本方法利用了4 个角度的线偏振图像，其光强值可分别表示为I0、I45、I90和I135。根据式（26），计算图像的Stokes 矢量；根据式（27）和（28），计算图像各像素点的偏振度值和偏振角值。

对偏振角值进行统计排序，选择出现概率最大的偏振角值作为大气光偏振角（θA）。同时，出现θA的像素群可认为不包含直接透射光或对应的直接透射光为非偏振光，即大气光特征参数估算有效像素群。根据式（27）可知，图像各像素点计算得到的偏振度值总是小于或等于大气光偏振度。因此，将有效像素群的偏振度最大值看作大气光偏振度值（pA），即

2）根据大气光偏振角特征参量和偏振度特征参量估算大气光强。由马吕斯定律可知

式中，和分别是x和y方向的大气光强分量，可分别表示为

结合式（30）和（32）、式（31）和（33），可得

考虑到分母接近于0 时会引入很大的误差，因此，将式（34）分为两式。计算出Ap后，可得大气光强为

3）更普遍的情况可能是场景图像中并不存在天空区域，此时按照下述方法估算无穷远处大气光强。结合式（20）、（23）和（24），可得

根据式（36），当L=A∞时，I=A∞。即除了天空区域，也可以从有直接透射光的区域估算无穷远处大气光强。将I0写成偏振部分和非偏振部分之和，即

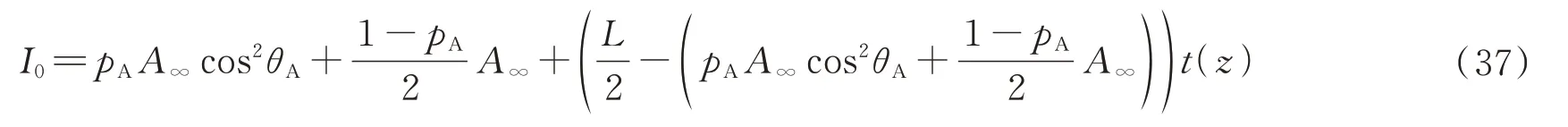
假设图像中所有的像素点均满足t→0，则式（37）右边第三项为0，此时得到的A∞的表达式记作为Am∞

实际上图像中绝大部分的像素点不满足该假设条件，因此，由式（38）计算得到的无穷远处大气光强用Am∞表示，以区分与最终计算得到的A∞。同时，根据式（36）可知，满足该假设条件的像素点有I=A∞的关系。此时，将式（38）得到的Am∞与I进行比较，最接近的像素点可认为是假设条件成立的像素点，其对应的光强即为A∞。

4）在估算得到了A和A∞后，根据式（25）可以计算得到最终的去雾图像。图15 所示为不包含天空区域的雾霾图像的去雾效果。从图中可以看出，提出的方法克服了传统偏振去雾技术需要天空背景限制的问题，提高了偏振去雾技术的实际应用价值。

图15 不含天空区域的偏振去雾成像结果［30］Fig.15 Polarimetric dehazing imaging result without sky area［30］

利用该方法开展了浓雾霾环境中的去海雾实验研究［30］。针对海雾变化快、浓度高的特点，在海雾出现时进行了连续拍摄，利用同一算法对不同浓度的海雾进行偏振去雾处理，去雾效果如图16 所示。可以看出在海雾快速变浓的过程中，提出的算法均可以恢复图像中大量的细节信息，表现出了较高的稳定性和鲁棒性。

图16 连续变化的海雾环境中偏振去雾效果Fig.16 Polarimetric dehazed images in continuously changing sea fog environment

3.1.2 结合图像处理技术的快速偏振光学成像去雾/去散射方法

偏振光学成像去雾/去散射技术原理简单，普适性好，但存在关键参数估算精度不高的缺点。为了提升关键参数估算精度，一般需要针对不同的散射介质环境或不同的偏振光学成像系统设置不同的偏置系数［76］，这将影响偏振光学成像去雾/去散射技术的自动化处理能力和实时性。为了克服该缺陷，开展了一系列结合图像处理技术的快速偏振光学成像去雾/去散射方法研究。

首先，利用熵函数实现自动判断最优偏置系数的功能［77］。在偏振光学成像去雾/去散射方法的实际处理过程中，一般会针对偏振度值进行偏置计算，引入偏置系数ε，以防止由于估算错误导致的去雾错误。即式（29）被改写为

ε的取值范围一般为1.0～1.6，不同的雾霾环境通常对应不同的ε最优值。为了使最优偏置系数取值自动进行，引入图像评价函数—熵函数。熵函数的定义式为

式中，pk是灰阶k的概率。熵函数是一种非常稳定的无参考图像评价函数，熵值越大，证明图像的细节分辨能力越强，图像质量越好。因此，在去雾处理时，通过扫描ε的取值，可以计算得到一系列的去雾图像，对这些图像进行熵函数计算，并与之前图像相比较，当熵值出现最大值时，输出最优去雾图像，并停止扫描，即完成了偏振光学成像去雾/去散射的自动化处理。

图17 所示为熵值随ε的变化曲线。从图中可以看出，当ε取不同值时，去雾效果图的熵值变化明显；当熵值即将到达峰值时，其变化变缓。因此，通过该方法可以自动处理和输出最优化的去雾图像。

图17 去雾图像熵值随ε 的变化［32］Fig.17 Variation of entropy value in dehazed image with ε［32］

其次，结合HSI（Hue，Saturation，Intensity）颜色空间实现快速偏振光学成像去雾/去散射处理［33］。在对彩色图像的偏振光学成像去雾/去散射处理过程中，由于RGB 三通道的场景偏振特性可能有较大差异，为了提高偏振去雾/去散射成像的可靠性，通常需要对三通道的图像分别进行关键参数估算和处理。然而，这种处理方法会很大程度上影响计算效率。为了克服该问题，提出了一种结合HSI 颜色空间的快速偏振光学成像去雾/去散射方法，其算法流程如图18 所示。

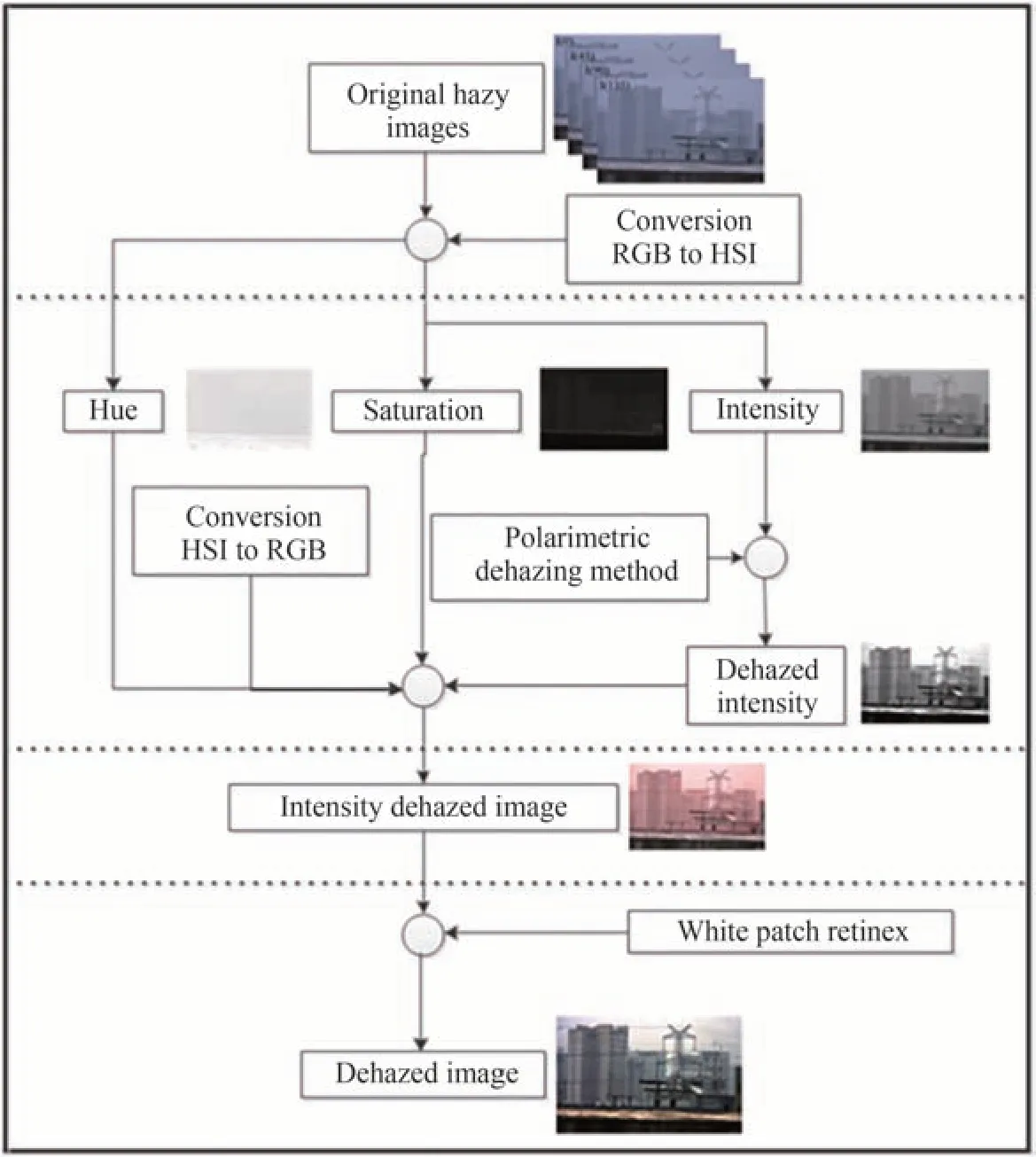
图18 HSI 颜色空间的快速偏振光学成像去雾/去散射算法流程［33］Fig.18 Workflow chart of dehazing/descattering algorithm for fast polarimetric imaging in HSI color space［33］

HSI 颜色空间与RGB 颜色空间的相互转化关系为

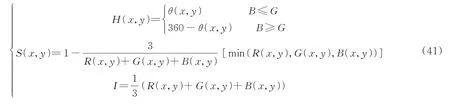
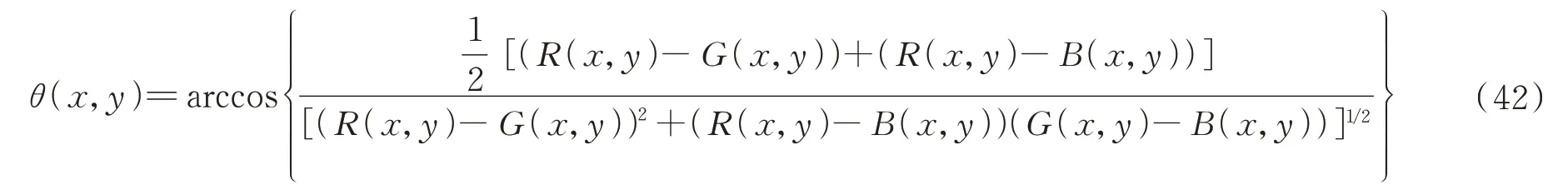
其中，对雾霾图像进行颜色空间转换后，仅需要对I 空间进行偏振去雾/去散射处理。相比于在RGB 空间进行处理，理论计算效率可提升3 倍。基于HIS 空间的偏振去雾处理效果如图19 所示。表3以4组图像为例，列举了不同的去雾/去散射方法所需的计算时间。表中，Tarel法［77］和直方图均衡化（His.Equ.）法［78］分别代表了图像复原型方法和图像增强型方法；后两列为不同颜色空间的偏振光学成像去雾/去散射处理所需要的计算时间，可以看出，相对于RGB 空间而言，基于HIS 空间的偏振光学成像去雾处理的实际计算效率提升超过了2倍以上。

表3 不同去雾/去散射方法的计算时间表［33］Table 3 Calculation schedule for different dehazing/descattering methods［33］

图19 基于HSI 颜色空间的偏振去雾处理效果［33］Fig.19 Polarimetric dehazed images based on HSI color space［33］

将基于HIS 空间的偏振去雾算法用于图1 所示的偏振相机，实现了实时去雾处理［12］。通过将自动化的偏振去雾/去散射算法移植到FPGA 模块上，实现了25 帧/s 的实时去雾显示。图20 所示为偏振光学成像相机拍摄后抽出的一帧裁切图像，（a）～（d）分别表示同一场景的0°、45°、90°线偏振和右旋圆偏振子图像。图21 所示为偏振光学去雾效果。

图20 偏振光学成像系统拍摄的一帧同一场景不同偏振图像［12］Fig.20 A frame with different polarizations of the same scene taken by a polarimetric imaging system［12］

图21 偏振去雾图像［12］Fig.21 Polarimetric dehazed image［12］

3.1.3 基于低通滤波去噪的偏振光学成像去雾/去散射方法

在成像过程中，数字图像对偏振处理影响很大。常规的相机输出为0～255 的离散灰度值，在计算偏振度和偏振角时，得到的结果并不总是可靠的，因此，估算关键参数时，需要设置偏置系数。同时，相机的本底噪声对关键参数估算的准确性具有一定的影响。因此，提出了一种基于低通滤波去噪的偏振光学成像去雾/去散射方法［34-35］。实验结果表明，该方法在浓雾处理中是全自动且有效的。本方法在光学监测、水下成像、生物组织成像等诸多应用中具有较大的应用潜力。

首先，估计出大气光的偏振部分

则，大气散射光可以写成

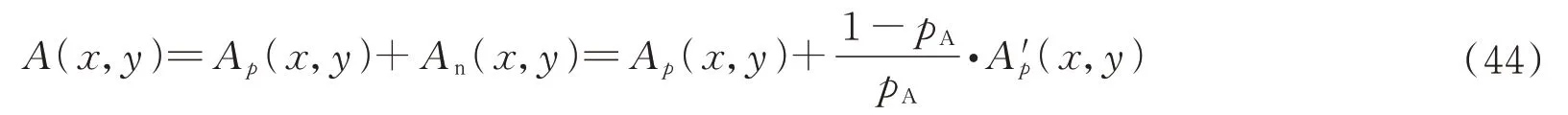
式中，An（x，y）是大气光的非偏振部分。由于pA非常小，An（x，y）比Ap（x，y）大很多，意味着计算出的A（x，y）中的噪声主要来自An（x，y）中的噪声。因此，首先使用低通滤波来抑制An（x，y）中的噪声，即

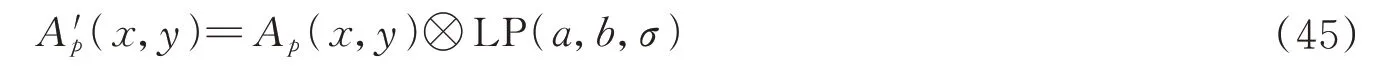
式中，“⊗”表示卷积，LP 表示低通滤波器，（a，b）表示滤波器的窗口大小。滤波器采用高斯低通滤波器，高斯核可以表示为

式中，（a0，b0）是高斯核的中心坐标，σ为窗口大小的1/5。实验中，将窗口大小设置为整个图像大小的0.5%。与式（35）相比，式（44）在实际应用中更加合理，保证了偏振去雾算法的鲁棒性和可靠性。

根据式（20），A∞应该是A（x，y）的最大值或比A（x，y）略大。从式（25）可以看出，A∞可以看作是一个系数，只影响去雾图像的平均灰度值，因此，为了使该方法的鲁棒性更强，将A∞设置为略大于A（x，y），以满足绝大多数散射环境应用条件。算法流程如图22 所示。

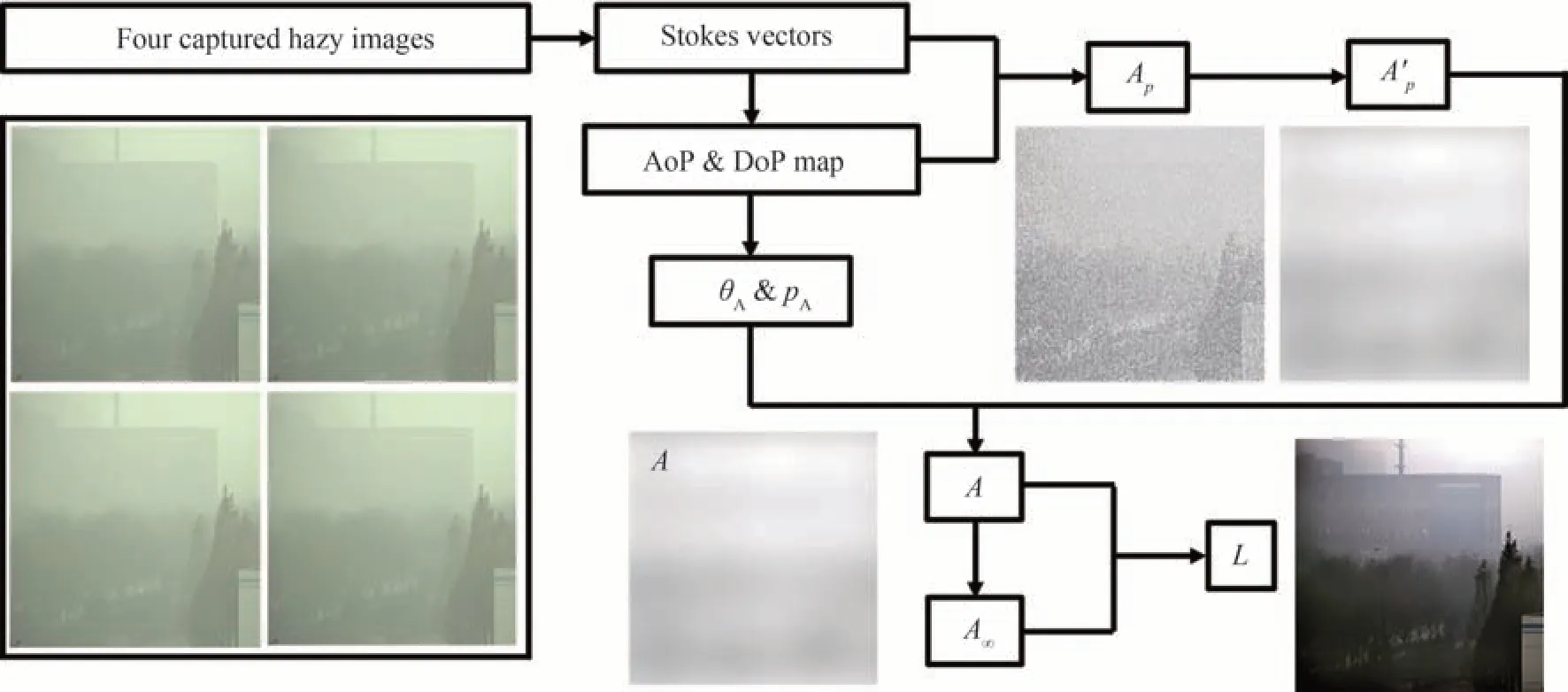
图22 基于低通滤波去噪的偏振光学成像去雾/去散射算法流程［35］Fig.22 Workflow chart of polarimetric dehazing/descattering algorithm based on low-pass filter denoising［35］

图23 所示为去雾效果，（a）为强度图；（b）～（d）分别表示Schechner 的偏振去雾效果、3.1.2 节提出的偏振去雾效果和基于低通滤波去噪的偏振去雾效果。从对比可以看出，相比于其他图像，图23（d）所示的基于低通滤波去噪算法的去雾结果的能见度和对比度都得到了大幅度提升，同时，图像整体细节复原能力最强。

图23 偏振去雾效果［35］Fig.23 Polarimetric dehazing results［35］

3.1.4 针对Lucid 分焦平面彩色偏振相机实时偏振去雾/去散射应用的软硬件模块化开发

利用Lucid 彩色偏振相机（TRI050-QC），开发了基于低通滤波去噪的实时偏振光学成像去雾/去散射上位机模块。通过优化算法和多线程处理，开发了实时彩色偏振光学成像去雾模块，目前帧率最高可以达到15 帧/s。上位机模块的整体结构如图24 所示。

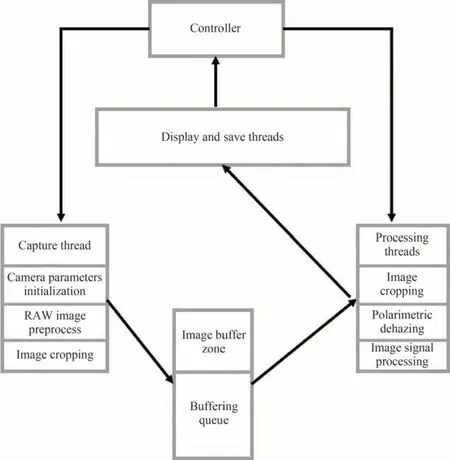
图24 实时偏振去雾/去散射系统的架构Fig.24 Architecture of real-time polarimetric dehazing/descattering system

软件的界面如图25 所示，其中第1 部分用于偏振相机所接收的0°、45°、90°、135°四个线偏振图像的实时显示；第2 部分用于实时显示去雾处理后的场景图像；第3 部分包括相机初始化、相机参数设置和显示设置三个部分，用来设置相机和图片显示格式；第4 部分负责图片和视频流的保存。

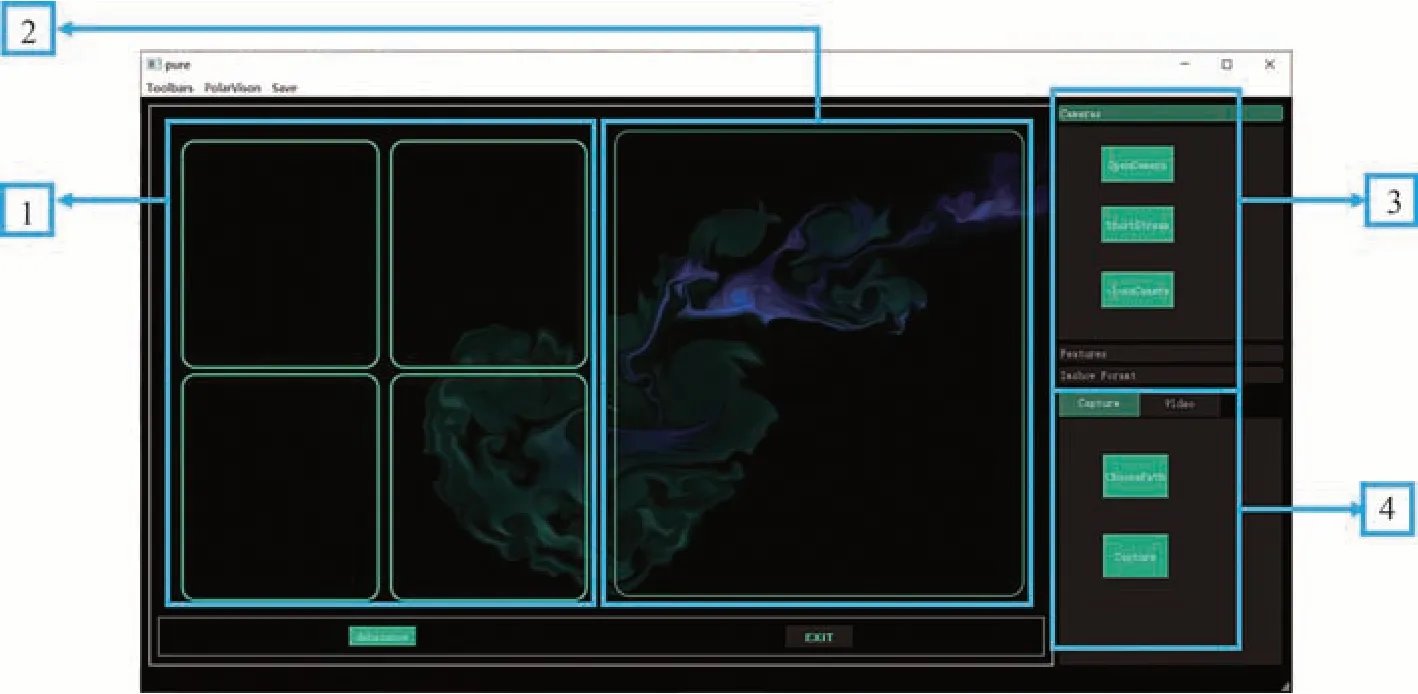
图25 实时偏振去雾/去散射成像软件界面Fig.25 Software interface of real-time polarimetric dehazing/descattering imaging

在室内，利用该系统进行了水下运动目标的实时去散射实验测试，截取一段视频流中的关键帧如图26所示。其中，（a）是原始图像，（b）是实时处理后输出的去散射图像，可以看出，该系统具有良好的水下去散射性能，近景轮廓细节信息得到了有效增强，远景一些近乎消失的信息也得到了有效恢复。

图26 视频流中水下去散射成像场景的一个关键帧Fig.26 A key frame of underwater descattering imaging scenes in video stream

在室外，利用该系统进行了重度雾霾环境下的实时去雾实验测试，结果如图27 所示。从视频流中取出关键帧进行比较，可以看出，实时处理效果显著。尤其是天空区域部分，原场景中完全无法看到的云彩形貌在处理后也得到恢复。

图27 视频流中户外实验场景的一个关键帧Fig.27 A key frame of outdoor descattering scenes in video stream

3.2 可见光/近红外偏振图像融合成像

偏振光学成像已经在可见光（400～700 nm）波段具有广泛应用，如目标检测［21］、材料识别［22］、大气和海洋传感［79-80］、生物和医学诊断［81-82］、三维成像［83-84］、去雾和水下去散射成像［30，85］和鬼成像［86］等。随着监视和防御领域特殊需求的增加，红外波段常常表现出可见光谱中无法探测到的独特的偏振特性［11，87］，使得短波红外（Short-Wave Infrared，SWIR）（0.9～1.7 μm）、中波红外（Mid-Wave Infrared，MWIR）（3～5 μm）和长波红外（Long-Wave Infrared，LWIR）（8～14 μm）偏振光学成像最先成为研究热点。然而，由于红外传感器的可用像素较少，像素尺寸较大，空间分辨率相对较低，所以通常将可见光成像与红外偏振光学成像相结合，并将它们的图像融合以获得互补信息［6，88］。

为了实现两幅图像的融合，它们的图像分辨率必须是相同的。然而，红外图像往往具有较低的空间分辨率，所以通常采用对可见光图像降采样的方法以匹配红外图像的低分辨率［89］，但是这种方法会导致可见光图像中部分细节信息的丢失［90］。为克服此问题，我们提出了一种可见光与近红外偏振图像的高分辨率融合方法。

由于SWIR 相机的像素尺寸远大于可见光相机的像素尺寸，所以SWIR 相机中一个像素捕捉到的物体区域会覆盖可见光相机的多个像素。对于同一视场区域，定义可见光相机和SWIR 相机所成像区域的像素数比例为

式中，d、f分别表示探测器的像素大小和相机镜头的焦距，下标S、V 分别表示SWIR 相机（以及对应的SWIR图像）和可见光相机（以及对应的可见光图像）。实验中所使用可见光相机（OK_AC1360，JoinHope Image Tech.）的像素尺寸为4.65 μm×4.65 μm，SWIR 相机（OWL 1.7-CL-320，Raptor Photonics Inc.）的像素尺寸为28 μm×28 μm。相机镜头的焦距相同，为f=50 mm。由式（47）可知，β约为6，意味着SWIR 图像的一个像素对应着可见光图像的6×6 个像素。

将SWIR 图像的一个像素上采样（即增加分辨率）为6×6 个像素，按式（48）依据可见光图像的像素灰度值（正比于强度值）直接给SWIR 图像的每个像素赋灰度值（正比于强度值）。

式中，上标H、L 分别表示高、低分辨率。由式（48）可知，重构的高分辨率SWIR 图像的强度首先由其低分辨率强度决定，同时其细节变化又与可见光图像的高、低分辨率强度之比有关。式（48）意味着在重构过程中可以充分保留SWIR 图像的强度，从而保持其偏振特性不变，但其细节信息将得到很大程度的增强。

高分辨率的SWIR 图像重构对恢复SWIR 中的偏振信息非常有利。四幅低分辨率SWIR 偏振子图像如图28（a）所示，重构后的高分辨率偏振子图像如图28（b）所示。可以看出，所重构图像的细节信息得到了有效增强。

利用图28 所示的SWIR 偏振子图像计算偏振度（DoP）图像和偏振角（AoP）图像，并将其与可见光波段的DoP 图像和AoP 图像进行比较，实验结果如图29 所示。图29（a）和（b）分别为原始低分辨率和重构高分辨率的SWIR 波段的DoP 图像，图29（d）和（e）分别为原始低分辨率和重构高分辨率的SWIR 波段的AoP 图像。图29（c）和（f）分别为同一目标可见光波段的DoP 图像和AoP 图像。可以看出，重构后的高分辨率SWIR 图像的偏振信息比低分辨率图像更丰富。

图28 一元硬币的原始低分辨率和重构高分辨率的SWIR 偏振图像［54］Fig.28 Original low-resolution and reconstructed high-resolution SWIR polarized images of one-yuan coin［54］

图29 一元硬币的偏振信息图像［54］Fig.29 Polarization information images of one-yuan coin［54］

另外，研究也表明，结合卷积神经网络（Convolutional Neural Network，CNN）的可见光与近红外高分辨率融合方法同样具有重要的应用价值。卷积神经网络已被证明可以有效地提高图像的空间分辨率［91-93］。该方法利用相同场景下彩色图像的高频相关性［94-96］重构高分辨率的SWIR 图像，虽然难以获得SWIR 图像的数据集，但由于反射率图像的子波段之间存在高频相关性，所以可以利用彩色图像对应的子波段对网络进行训练，然后利用训练好的模型对SWIR 图像进行重构。

整个重构过程分为三个步骤：1）构建训练数据并训练网络；2）利用训练的模型重构高分辨率近红外（Near Infrared Ray，NIR）（760～900 nm）图像；3）利用验证后的网络来重构高分辨率SWIR 图像。

图30 所示是用于重构高分辨率SWIR 图像的CNN 网络架构，利用彩色图像的三个通道图像进行网络训练［97］。用G 通道图像训练R 通道图像，输入端为两个通道的数据矩阵，一个是R 通道的低分辨率图像，一个是G 通道提取的高频图像。各通道图像之间的高频相关性为重构过程提供必要的信息，有效地增强重构图像的保真度。

图30 高分辨率卷积神经网络架构［97］Fig.30 High-resolution convolutional neural network architecture［97］

构建训练数据集的第一步是选取彩色图像的一个通道作为参考，从该通道的图像中提取高频信息；然后根据式（47）对其他通道的图像进行下采样，构建低分辨率数据。由于下采样过程主要基于β，因此该数据集的下采样图像是真实值的1/36。生成10 000 张大小为264×264 像素的图像作为训练样本，且有另外1 000 张图像作为验证数据。

训练好的网络可以应用于NIR 高分辨率图像重构。利用RGB+NIR 相机采集470～900 nm 波长的图像。彩色图像训练的模型网络输出如图31 所示，图31（a）～（d）分别表示低分辨率NIR 图像、重构的高分辨率NIR 图像、参考图像和G 通道图像。可以看出，与图31（a）相比，图31（b）的空间分辨率得到了有效提高，特别是面部的细节信息。对比图31（c）和（d），可以看出由于光照不同，细节信息有很大的区别，且图31（b）的强度分布与图31（c）能够很好地吻合。

图31 近红外图像的重构结果［97］Fig.31 Reconstruction results of NIR image［97］

该目标的偏振图像如图32 所示，其中图32（a）～（d）为DoP 图像，图32（e）～（h）为AoP 图像。从图32（a）和（b）的对比可以看出，一些DoP 高的区域得到了恢复，如眼睛的轮廓；从图32（b）和（c）的对比可以看出DoP 分布基本相同；从图32（e）～（h）的对比可以看出AoP 图的分布也基本相同。这意味着在有效增强NIR 图像空间分辨率的同时，很好地保持了图像的原始信息。

图32 目标的偏振信息图像［97］Fig.32 Polarization information images of the target［97］

图33 为重构高分辨率SWIR 图像的实验结果。直接采集的低分辨率SWIR 图像和彩色图像分别如图33（a）和（c）所示。与彩色图像相比，SWIR 图像的空间分辨率要低得多，并且在平面模型边缘可以清晰地看到锯齿现象。图33（b）是使用彩色图像训练模型重构的高分辨率SWIR 图像。从图中两个黄色框内的数字可以看出，该方法有效地消除了锯齿现象，提高了图像的空间分辨率。实验结果表明，利用该方法重构的SWIR 图像具有良好的质量和保真度。

图33 飞机模型的SWIR 成像实验结果［97］Fig.33 Experimental results of SWIR imaging of a plane model［97］

同样的，针对低分辨率SWIR 偏振图像的高分辨率重构如图34 所示，其中图34（a）～（c）分别为低分辨率SWIR 波段、重构的高分辨率SWIR 波段和可见光波段的线偏振度（Degree of Linear Polarization，DoLP）图像，图34（d）～（f）分别为低分辨率SWIR 波段、重构的高分辨率SWIR 波段和可见光波段的偏振角（AoP）图像。可以看出，SWIR 和可见光图像的偏振特性有较大区别，尤其是平面模型体，分别如图34（a）和（c），以及图34（d）和（f）所示。图34（b）和（e）表明，该重构方法恢复了边缘的细节信息，重构后的SWIR 图像整体偏振信息与低分辨率SWIR 图像一致。图34（a）和（b），图34（a）和（c），图34（b）和（c）的峰值信噪比（Peak Signal to Noise Ratio，PSNR）分别为38.233 2、24.788 4 和22.836 7，说明低分辨率和高分辨率SWIR 波段的DoLP 图像之间的PSNR 要高得多，具有更高的相关性。

图34 SWIR 偏振图像的高分辨率重构［97］Fig.34 High-resolution reconstruction of SWIR polarimetric images［97］

3.3 偏振3D 重构成像

传统的成像系统采用摄像机对周围景物拍照，将三维（3D）景物的强度、光谱、偏振等信息记录到二维（2D）像平面中，失去了目标的深度信息。3D 成像技术能够补偿传统成像系统对目标深度信息探测的缺失，在未来计算机视觉的发展中占据着重要的地位。常见的光学3D 成像技术有飞行时间法、立体视觉法和结构光3D 成像等［98］，存在成像装备昂贵或实现过程复杂等限制。近年来，偏振3D 重构成像技术以其重构速度快、装置简单等优点，成为了光学3D 成像技术的研究热点。

3.3.1 偏振3D 重构成像物理模型

由菲涅尔反射原理可知，自然光入射到物体表面，反射光和透射光为部分偏振光。图35 给出了偏振3D重构成像物理模型示意图。当光入射到物体表面时，入射光线、表面法线和反射光线形成入射平面，反射角等于入射角，用θ来表示。反射光线的传播方向定义为Z轴正方向，对应的xoy平面为相机的成像面。反射角θ是表面法线与Z（z）轴正方向的夹角，即物体表面法线的天顶角。物体表面法线投影到相机成像面上，与x轴的夹角ϕ表示方位角。研究表明，目标表面反射光的偏振信息（偏振度DoP 和偏振角AoP）与其表面的法线方向信息（天顶角θ和方位角ϕ）之间存在一定的函数映射关系，因此通过偏振相机获取目标表面反射光的偏振信息，再根据偏振信息获取目标表面法线的方向信息，进而通过法线积分重构物体的3D 形状［99］。

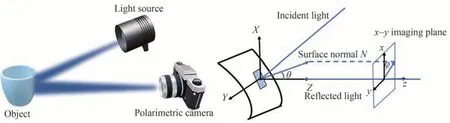
图35 偏振3D 重构成像物理模型示意图Fig.35 Physical model schematic of polarization 3D reconstruction imaging

3.3.2 偏振3D 重构成像基本理论与方法

实现偏振单目3D 重构成像，首先需要获取目标表面反射光的偏振图像信息。获取偏振图像最简单的方法是在普通相机的镜头前增加一个可旋转的线偏振片，通过旋转线偏振片的方式获取目标多个角度的偏振图像，但该方法以牺牲采集时间为代价来获得成像器件的全分辨率图像。如图35 所示，采用分焦平面偏振相机拍摄目标，即可获得目标上任意一物点的偏振度DoP 和偏振角AoP 信息。该相机焦平面前放置了由0°、45°、90°和135°方向的微偏振片组成的线偏振片阵列层，每个微偏振片对应像平面的一个像元，即单个像元可以获取一个线偏振片角度下的强度值。通过采集目标的偏振原始图像，将其分解为0°、45°、90°和135°的四幅偏振子图像，根据偏振子图像求解Stokes 参量，进而得到线偏振度（DoLP）图像（由式（27）计算）和偏振角（AoP）图像（由式（7）计算）。

根据菲涅尔反射原理，自然光照射到目标上时，目标表面漫反射光的偏振度DoP 与目标表面介质折射率n和表面法线天顶角θ有关［99］，即

根据式（49），图36 给出了不同折射率材料漫反射光的偏振度DoP 随入射角θ的变化关系。可以看出，DoP 随着θ的增大而单调递增，且变化显著；相对而言，材料折射率差异对DoP 变化的影响要小得多，为此，采用固定的折射率值（n=1.5）来近似计算目标图像中每个像素所对应的天顶角。式（49）表明，当表面折射率确定时，漫反射光的DoP 与物体表面法线的天顶角θ是一一对应关系，通过数值计算方法获得图像中每个像素对应的物体表面法线的天顶角θ。

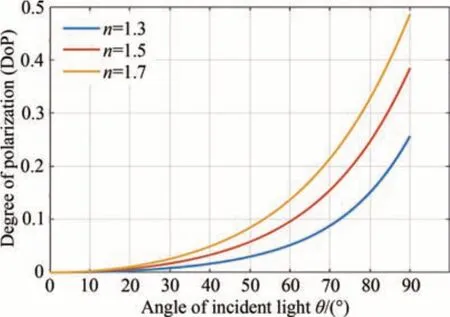
图36 不同折射率材料的漫反射光的偏振度随入射角的变化Fig.36 Variations of DoP of diffuse reflection light with incident angle θ for materials with different refractive index

需要说明的是，如式（7）所示，偏振相机成像直接给出偏振角AoP 的取值范围为［0，π］；而如图35 所示，目标表面法线方位角ϕ的取值范围为［0，2π］。因此，基于偏振3D 重构成像原理，由反射光的AoP 确定方位角ϕ时，存在方位角歧义问题，即

对基于反射光偏振信息的3D 重构成像模型进行分析可知，物体表面法线的天顶角在很小的情况下，方位角可能发生突变。针对具有对称性的物体，当入射光是自然光时，所获得法线的天顶角数值在相机能够拍摄到的物体区域内是对称的。我们提出了基于天顶角特征的方位角去歧义方法［53］，获取了目标表面法线确定的方位角ϕ。对于笛卡尔坐标系中任意一个给定物体的表面，假设物体表面是均匀、平滑的连续平面，则物体的曲面方程可以表示为f（x，y），表面法向量N可表示为式（51）。根据天顶角θ和方位角ϕ即可求解表面法线方向，最终利用法线积分算法恢复目标表面的3D 形状。

3.3.3 偏振3D 重构成像实验结果

根据所提方法进行实验，选用表面材质均一、连续光滑的物体作为目标，以纸杯为例拍摄它的偏振图像以计算表面法线并恢复其表面形状。图37 给出了表面粗糙纸杯的偏振3D 重构成像结果。图37（a）和（b）分别为纸杯的强度图和3D 重构图，图中x轴与y轴分别表示目标图像的像素坐标，灰度大小表示所重构目标的深度信息。结果表明纸杯重构深度图能够体现其3D 形状，方位角歧义引起的误差导致的畸变被校正。

图37 纸杯的偏振3D 重构成像结果Fig.37 Reconstructed 3D polarimetric imaging result of paper cup

为了验证所提方法可应用于不同表面材质的目标，拍摄了相同形状不同表面材质目标的图像，重构了其3D 形状。图38 所示为不同表面材质的圆柱体，其中，图38（a）是塑料材质圆柱体模型的强度图，图38（b）是在圆柱体模型表面贴一层光滑的白色相纸后拍摄的强度图，图38（c）是在圆柱体模型表面贴一层粗糙的白纸后拍摄的强度图。

图38 不同表面材质圆柱体的强度图Fig.38 Intensity images for cylinder with different surface materials

塑料材质圆柱体模型与光滑相纸相比，表面较粗糙，存在材质不均匀的区域，其表面反射光的类型以漫反射为主；圆柱体粘贴光滑相纸后表面材质均一，反射光的类型混合了镜面反射和漫反射，存在部分区域的耀光；圆柱体粘贴粗糙白纸后表面材质均一，反射光的类型以漫反射为主。通过对不同表面材质的圆柱体模型进行3D 重构，分析目标表面材质对所提出的单目3D 重构成像方法效果的影响。分别对图38 所示的三种表面材质的圆柱体进行3D 重构成像，结果如图39 所示。

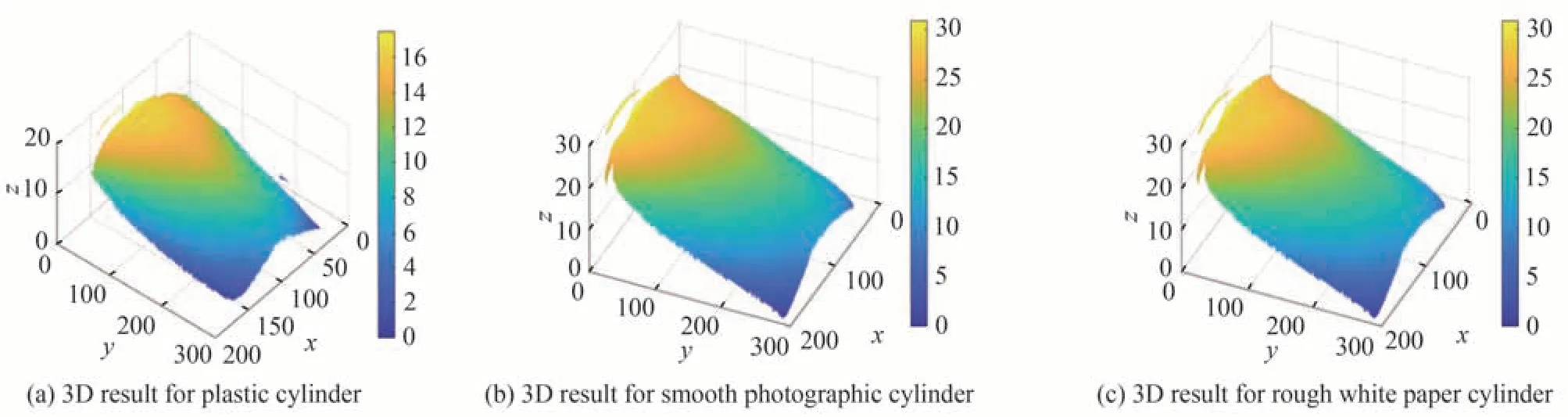
图39 不同表面材质圆柱体的3D 重构结果Fig.39 3D reconstruction results for cylinder with different surface materials

重构结果表明，所提出的单目3D 重构成像方法可应用于不同材料的物体表面，并且能够在不受耀光影响的情况下重构物体的3D 形状，而目标表面材质的均匀性会影响偏振3D 重构成像的效果。图39（a）中塑料材质圆柱体模型的边缘区域重构深度存在毛刺；图39（b）、（c）中表面粘贴均匀的光滑相纸和粗糙白纸的圆柱体模型重构结果中，边缘的重构深度数据平滑、无畸变。同时，图39（b）、（c）中的重构结果表明，表面材质均一的目标，其粗糙程度对3D 形状的重构结果影响不大。

偏振3D 重构成像方法可实现单目3D 成像，具有计算时间短、重构精度高、信息获取手段简单、对环境光要求低、无需图像配准、实时性好等优点，具有重要的发展潜力和应用价值。

4 总结与展望

偏振是光的一个重要“信息维度”参量，通过测量光与物质相互作用过程中的光波偏振信息可以获得物质的诸多特性。近年来，偏振信息测量特别是偏振光学成像探测技术，在材料分析、目标识别、缺陷检测、环境监测、病变诊断、伪装去除、透雾透散射介质成像等领域，发挥着重要的应用价值，也取得了令人瞩目的研究成果。本文对国内外关于偏振光学成像探测技术的研究现状、偏振相机的研制开发情况及其应用状况进行了综述；结合研究团队多年来在该领域的工作，介绍了全偏振态同时探测的分孔径偏振相机及分孔径偏振光学成像镜头，以及在偏振去雾去散射、偏振图像融合、偏振3D 重构等偏振光学成像探测方面开展的一些工作，主要涉及分孔径偏振光学成像系统的设计及关键器件和技术，偏振图像的信息处理技术及算法和应用等方面。

需要说明的是，图像处理算法和偏振光学成像技术均可在一定程度上实现改善成像质量、提升图像对比度、增强和凸显目标的目的，但是也必须看到二者之间的固有差异。以图像处理去雾和偏振去雾为例来分析说明基于图像处理算法和基于偏振光学成像技术的一些内在本质差异。

首先，图像处理算法和偏振光学成像技术发挥效能的物理基础不同。偏振信息从本质上讲是直接的光学手段，偏振去雾依据物理退化模型进行目标信息恢复和增强，而图像处理去雾是基于图像像素之间的相对关系，纯粹通过数字图像处理进行图像的增强或复原，不考虑光学信息演化或退化的物理过程。因此，两种去雾方法存在鲜明的内在差异：1）图像处理去雾的稳定性和可靠性较差。对于不同场景或同一场景不同雾霾天气，图像处理去雾效果具有明显的差异。这是因为图像去雾处理过程中需要利用先验知识或者假设前提，在先验不适用或假设不成立的情况下，图像会产生严重的失真。而偏振去雾立足于Mie 氏散射理论，适用于所有均匀的散射介质，因此去雾的稳定性和可靠性较高。2）图像处理去雾效果较差。图像处理去雾的原理一是图像增强，二是图像复原。图像增强去雾主要为凸显图像中难以分辨的细节信息，在这个过程中，很容易将某些微弱的细节信息误判为噪声而被去除，导致去雾图像的细节丢失。图像复原去雾主要表现为利用物理模型对退化的图像进行复原，从已报道的主流图像复原算法实验结果可以看出，该方法的颜色恢复能力差。相比较而言，偏振去雾方法可获得更加自然的去雾效果，图像细节和颜色恢复能力强。3）图像处理去雾计算效率较差。图像处理去雾方法（特别是图像复原方法）需要花费长时间进行去雾计算，而偏振去雾算法效率要高很多。

其次，偏振去雾技术相对图像处理去雾具有机理上的优势。偏振去雾技术基于雾霾状况下的大气物理退化模型，通过采集多幅不同偏振方向的图像获得散射噪声光信息，利用光学手段反演退化过程、获得退化前的场景清晰图像，细节信息完整、颜色保真度高；而图像处理去雾技术基于图像增强或复原技术，利用像素间的强度关系判断目标和噪声，易导致图像信息丢失、颜色失真。

最后，偏振去雾技术相对图像处理去雾具有更好的鲁棒性。偏振去雾算法对不同浓度、不同粒子成分、不同目标均可获得清晰图像输出，算法普适性和实时性强；而图像处理去雾受限于先验信息，不能保证总能获得稳定的去雾效果，需要根据天气情况人为干预，算法鲁棒性和实时性差。

目前，偏振光学成像探测技术研究方面仍存在以下几个值得思考和需要解决的问题：

1）关于偏振测量精度的提升问题

偏振相机是基于偏振调制和光强度测量工作的，所以高精度、准确地获取光的偏振信息是该技术及其实际应用的基础和基本要求。以分焦平面偏振相机（DoFP）和分孔径偏振相机为例分别进行分析说明。

分焦平面偏振相机（DoFP）存在的几个固有缺点需要进行克服或校正：首先，由于微纳加工工艺的限制，微偏振片阵列在主次透过率、消光比及偏振角度等性能参数方面无法达到理想的设计要求，在空间排布上会产生非均匀性，从而影响偏振图像的重构。其次，光电传感器在响应过程中也会由于量子效率、增益与暗电流等像素间差异因素而产生随时空变化的非均匀性误差。最后，微偏振片阵列四个检偏通道的空间错位排布使其在成像过程中无法实现完全采样，特定检偏通道只能探测到该通道的偏振信息，无法探测到相同空间位置处其他三个通道的偏振信息。不同空间位置的偏振通道所采集的偏振信息被用于重构入射光的偏振态时便会产生固有误差—瞬时视场角（Instantaneous Field of View，IFOV）误差，典型表现为在边缘处出现锯齿状伪像（重构误差）。针对上述三个问题需要采取不同措施进行相应的校正：首先，需要通过提高金属线栅微偏振片阵列的加工精度，提升消光比，减少插入损耗，提高偏振调制精度，尽可能减小物理层面的误差影响。目前国际上Sony 公司的IMX250MZR 探测芯片，其消光比可达300∶1 以上，而国内目前还没有突破50∶1，所以工艺水平仍需不断提升［100］。另外，需要对系统进行非均匀性校正，以减小探测过程中产生的非均匀性误差，将重构入射光偏振态所需的Stokes 参量校正为理想响应值。其次，为了减小各类噪声对重构入射光偏振态的影响，要对偏振图像进行去噪处理。最后，为了减小IFOV 误差，需要研究Stokes 参量超分辨率重建算法，例如基于插值、基于频域滤波、基于深度学习等估计方法。

分孔径偏振相机尽管其结构紧凑、适合于对动态目标进行全Stoke 矢量的偏振光学成像探测及应用研究，但其由于四通道的装配误差等，必须要做好偏振子图像间的亚像素级配准；另一方面，由于其前端光学系统为望远系统，当在近距离条件下使用时，为了保证成像质量和实现清晰成像，需要在分孔径偏振相机前添加双胶合透镜。因此，需要对近距离使用时的分孔径偏振相机先进行标定与去畸变，然后利用去畸变后的分孔径偏振子图像进行图像配准，最终实现对近距离场景目标的偏振光学成像。

2）关于偏振光学成像系统的优化设计问题

围绕着同时获取目标的多个偏振子图像，需要不断创新光学系统设计理念和方案，同时尽可能地减少光学系统的复杂性。为此，逐步追求模块化、功能化和集成化是偏振光学成像系统设计的要求和发展趋势。研究已经表明，我们所提出的分孔径偏振光学成像镜头是一个创新思路。将普通相机镜头拿掉，更换成专门设计的全偏振态同时探测的分孔径偏振光学镜头，是实现偏振光学成像和研制偏振相机的一种便捷技术方案。这种全新的设计思路架构，最大限度地借助和利用了普通商用相机的已有硬件物理基础，把工作重心放到了硬件和软件这两大部分工作，其中，硬件主要完成镜头改制，包括基于分孔径技术的四种偏振态同时探测的偏振光学成像镜头的设计、加工、装配；软件主要完成图像配准、偏振定标、偏振光学成像去散射图像分析与增强算法。

3）关于偏振图像信息处理和挖掘及充分发挥计算光学成像优势问题

偏振光学成像从本质上讲隶属于计算光学成像，而计算光学成像是集几何光学、信息光学、计算光学、现代信号处理等理论于一体的新兴交叉成像技术研究领域，其利用数学模型精确描述，进而通过计算方法重构图谱，亦可根据系统衰变和误差模型提高图谱质量［101］。对于偏振光学成像探测而言，首先，需要注重图像信息处理和挖掘、软件算法优化设计，充分发挥计算光学成像的优势，特别是针对现有偏振相机存在的固有技术瓶颈，通过高精度定标方案来校正和复原真实偏振信息、针对改善成像质量的信息处理和挖掘技术还远远没有发挥出来。其次，需要注重多模态、多源图像数据的融合，实现优势互补，超越单模态、单源数据的局限性。同时，必须清楚地认识到，偏振光学成像探测技术仍然是传统强度和光谱成像的有益补充，并非总是万能的，当在传统强度和光谱成像受限的某些特定情况或环境下，该技术可以作为辅助手段进行有益尝试。研究也已发现，在某些特定情况下，它确实可能会发挥独一无二的作用，这部分研究工作在未来仍需不断尝试和积累。

4）关于偏振光学成像探测的应用问题

偏振光学成像探测技术和偏振相机在工业、农业、环境、医学、军事和民生等诸多领域均具有广泛的潜在应用，而且，不同的应用场合或场景，需要量身定做偏振光学成像系统及开发专用偏振相机。因此，发展到目前为止，我们认为该技术领域真正的痛点是，必须进行细致的行业分析，找到最佳的典型的专业应用突破口。需要聚焦应用领域，以典型应用带动和促进技术发展。以下三个方向可能是不错的选择，包括工业自动化生产线上产品缺陷或异物的机器视觉检测；生物医学领域中肿瘤病变组织的诊断；烟雾霾等复杂气象条件及低照度环境下暗弱小目标的清晰成像与监控。

致谢：感谢研究团队王庆飞、张诗荣、杨瑞、窦文涛、杜栋凯、魏寒月同学在材料整理和校对等方面的工作和帮助。