飞秒光场中锂原子三重电离的光电子关联动量与能量谱研究（特邀）

刘士炜，叶地发，刘杰

（1 北京计算科学研究中心，北京100193）

（2 北京应用物理与计算数学研究所，北京100088）

（3 中国工程物理研究院研究生院，北京100193）

0 引言

飞秒强激光场与原子相互作用是探索原子内部结构及其运动规律的主要实验技术之一，其研究热点集中在激光场驱动的电子再碰撞过程中的高阶阈上电离、高次谐波产生以及非序列电离等现象［1-2］。随着激光技术以及实验测量手段的发展，原子多重电离中的电子关联逐渐成为当前强场领域所关心的热点问题之一［3］。近年来，许多研究分别在实验与理论上成功探索了强激光场中稀有气体原子的双电离动力学过程中的电子关联［4］。此外，在一些三重电离、四重电离的实验观测中也看到了再碰撞引起的所谓的“膝盖（knee）结构［5］”以及在长波长范围内可能存在从（e，2e）到（e，ne）的散射机制［6］，即多个电子同时发生再碰撞电离。对于更高电荷态离子，相对论效应和磁场效应的出现将使电子关联行为更为复杂［7-9］。理论上通常可以用完整的量子力学描述激光与原子相互作用。然而到目前为止，仅获得了针对激光驱动氦原子的含时薛定谔方程（Time Dependent Schrödinger Equation，TDSE）的数值解［10］。也有一些近似的方法用以研究多重电离，例如通过一维TDSE 来探讨锂三重电离过程中关于波函数对称性的作用［11］以及采用时变紧密耦合（Time Dependent Close-Coupling，TDCC）方法研究锂电离过程中四体Coulomb 问题的碎裂构型等［12-14］。另一方面，一些工作成功地利用了费米分子动力学方法（Fermionic Molecular Dynamics，FMD）来研究激光原子相互作用、激光分子相互作用以及激光团簇相互作用［15］。此模型是利用Heisenberg 势与Pauli 势的辅助排斥势对经典轨道方法进行量子修正［16］。近年来，一些研究成功运用该模型研究了碳原子在强激光脉冲下响应的四重电离［17］、激光驱动单个氙原子中六个价电子的动力学过程［18］、强激光场中铷原子［19］以及氩原子的电离等［20-21］。

本文通过改进的多电子原子系统的动力学经典轨道蒙特卡罗（Classical trajectory Monte Carlo with the Heisenberg potential，CTMC-H）模型［19，22］来研究激光驱动锂（lithium，Li）原子的电离问题。该方法是在传统的经典轨道模型的基础上引入了Heisenberg 势的量子修正。通过最小化系统哈密顿方法并对照实验上锂各个价态的电离能，获得了锂原子的基态稳定构型，并通过求解经典牛顿方程研究了强度范围为1013W/cm2至1017W/cm2的锂的总电离概率。我们发现在锂的双电离和三重电离中都存在基于再散射机制的非序列电离过程。通过Li3+的相关动量谱重点研究了三重电离中的再散射行为。此外，根据Dalitz 图［23］中映射的电子能量分布，发现在非序列三重电离中存在清晰的电子关联印记。若没有特殊说明，本文中的公式符号均采用原子单位制（atomic units，a.u.）。

1 经典多体模型

在研究电子碰撞等问题中，传统的经典轨道蒙特卡罗（Classical Trajectory Monte Carlo，CTMC）方法是将电子视为经典点粒子，在充分考虑电子与原子核以及电子与电子之间的库仑相互作用的情况下，利用经典牛顿运动方程来求解电子随时间演化的动力学过程。电子的初始动量和位置通过蒙特卡罗随机取样获得，例如束缚电子的初始分布可以从具有固定总能量（一般是原子的基态能量）的微正则系综中取样［24］。但是在对于多电子原子动力学的模拟中，由于不存在束缚电子的能量下限使得经典方法描述的原子会发生非物理的自电离而不稳定。基于Heisenberg 势与Pauli 势修正的FMD 方法［16］可以成功的模拟高Z原子的经典稳定构型［25］，并在涉及多体碰撞和强场电离等方面有重要应用［19，22，26-28］。本文模型是基于经典方法的改进［29］，系统的哈密顿量为

式中，电子i的位置和动量分别用ri和pi表示。在电子与核的相互作用中引入Heisenberg 势的量子修正来模拟Heisenberg 不确定原理，其目的是为了禁止电子进入量子力学禁止的经典相空间区域［16］，其形式为

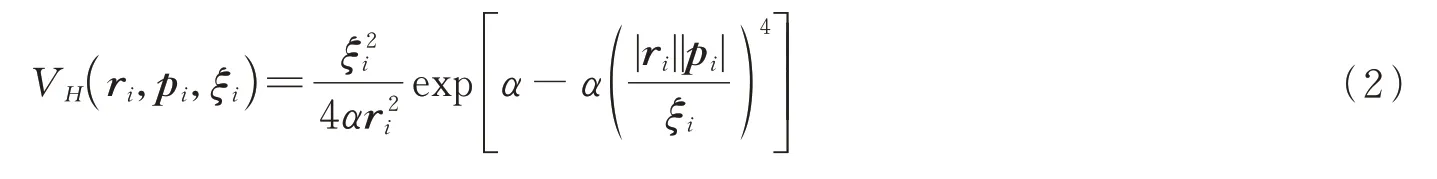
式中，参数α控制Heisenberg 势的刚性，ξi用以拟合原子的电离能并形成稳定的准经典基态构型，可以通过∂H/∂ri=0，∂H/∂pi=0 来确定，即体系所有可能出现的运动状态中，基态的能量处于极值。在本文模型中N=Z=3。通过将电子一个接一个地添加获得锂元素各个价态的哈密顿量并在每个步骤中重复上述操作，获得了Li 原子的电子初态构型，其中3 个电子处于同一平面上并显示了明显的壳层结构，内壳层的两个电子成对地排列在原子核周围，外层的电子离原子核的距离比其他两个电子稍远，稳定构型的相关参数为Ip1=0.198，Ip2=2.780，Ip3=4.500；ξ1=1.569，ξ2=0.992，ξ3=0.954；r1=2.408，r2=0.361，r3=0.398，如图1 所示。我们注意到位于同一壳层的两个电子离核距离r2、r3的取值略有不同，这是因为（与先前的FMD方法［16］不同）引入了不同的拟合参数ξi来精确模拟锂原子各个价态的电离能。

图1 锂原子基态的经典电子构型以及锂原子随激光强度变化的电离率，激光波长为800 nmFig.1 The configuration of classical lithium atom and the ionization rate of Li as a function of the laser intensities，the laser wavelength is 800 nm

系统的哈密顿量式（1）在所有位置向量和所有动量向量的单独旋转下是不变的［30］。这意味着H(r1，r2，r3；p1，p2，p3)=H(Ω1r1，Ω1r2，Ω1r3；Ω2p1，Ω2p2，Ω2p3)，其中Ω1和Ω2是两个不同的Euler 旋转操作。这一事实在模拟中被用来生成具有相同总能量的电子的随机初始条件。针对上述基态构型利用蒙特卡罗采样技术随机Euler 旋转来获取Li 原子基态下具有不同初始位置和动量的电子系综［29］。线极化激光场的电场的形式取E(t)=E0f(t)cos(ωt)ex，其中E0和ω分别是激光场的振幅和频率，包络函数为f(t)=sin2(πt/T)，T为脉冲长度，激光磁场B由ez×E/c给出，其中c是光速。

2 主要结果

2.1 Li 原子的多重电离率

在本文的模拟中，激光场与锂原子相互作用的系统动力学由正则方程描述，这是因为强激光能够将电子加速到足够大的速度，使得电子的德布罗意波长（电子位置的不确定性）远小于其在强激光场中的抖动距离（电子轨迹的典型空间尺度）；以800 nm，1 PW/cm2的线偏振激光为例，电子在光场中的抖动速度为vquiver=E/ω≈3 a.u.，对应的德布罗意波长为λ=h/vquiver≈0.3 a.u.而电子在光场中的抖动距离λquiver=E/ω2≈50 a.u.远大于λ。本文后续主要关注远大于1 PW/cm2强度的激光场中的原子电离过程。因此，在计算中，经典轨道方法可以近似描述电子的动力学过程。使用标准的4～5 阶Runge-Kutta 方法来数值求解3 个电子的经典动力学方程，且根据电子的最终能量是否为正来判断电离轨道［31］。对应每一个确定的激光参数，跟踪超过106条不同初始条件下的经典轨道以确保统计结果的收敛性。每条轨道的电子初始状态由蒙特卡罗采样技术对Li 原子的基态构型进行随机Euler 旋转得到。在追踪大量轨迹后获得电离率Pn=kn/ktot，其中kn是末态离子的电荷数为n的电离事件的轨道数，而ktot是模拟的总轨道数。图1（b）是800 nm 线偏振激光中强度范围在0.01 PW/cm2至250 PW/cm2的Li 的各个价态的电离率曲线，激光的脉冲宽度T=25 fs。由于Li 原子属于电子结构较为特殊的碱金属元素，第一电离能Ip1很小即最外层电子很容易发生电离，而次外层电子由于相对大的电离能而较难电离，于是发现在很长的激光参数范围内主要通道是单电离。因此，由再碰撞引起的双电离膝盖结构的激光参数范围也很长［4，31］。本文更关心的是三重电离通道，这主要是因为三重电离包含了两个电子以上的电子关联。可以看到三重电离的激光参数大约在大于3 PW/cm2的强度范围内。而在约60 PW/cm2时，Li3+的离子产量出现膝盖结构的拐点［32-33］，即激光强度小于60 PW/cm2的三重电离属于非序列三重电离。

2.2 Li3+离子的动量谱

电离后的离子动量谱可以为研究电离的整个过程提供更为丰富的动力学信息。根据动量守恒，利用电子的末态动量计算三重电离Li3+的动量分布。将锂原子体系的能量写为

式中，Pion表示锂原子核的动量。在这里将原子核、三个电子之间的相互作用记为V。因此能量随时间的变化为

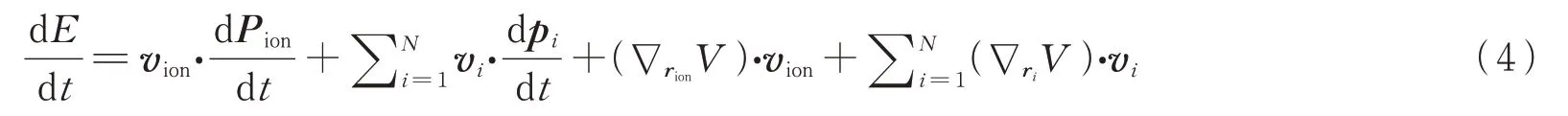
式中，vion，vi分别表示原子核以及三个电子的速度。根据带电粒子在电磁场中的洛伦兹方程

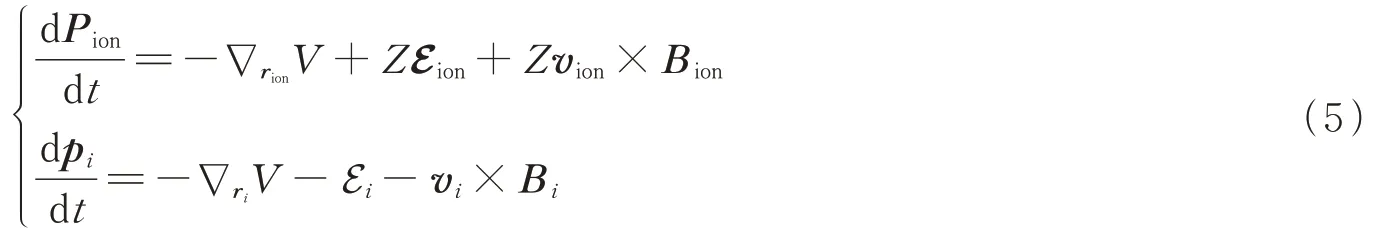
将式（5）带入式（4）得到

式中，Pk、pk，i分别表示原子核以及三个电子在激光传播方向（k=E×B）的动量，c是光速。在激光场与锂原子相互作用的过程中，电子通过吸收一定的光子能量来克服库仑势的束缚，根据能量守恒有nℏω=Eion+其中Eion和Ei分别表示原子核与电子的末态能量，Ipi为电离能，n是锂原子体系吸收的光子个数。在电离过程中，光子的线动量Δpk=nℏω/c会传递给电离电子和原子核，即nℏω/c=［Eion+结合式（6）可以看出，系统沿激光传播方向动量的改变量正比于体系总能量的改变量，比例常数为1/c［34］。因此，Li3+激光电场极化方向、磁场极化方向和传播方向末动量（PE，PB，Pk）为

对比图2（a）与（d），发现强度为20 PW/cm2下Li3+在激光极化方向PE的动量分布呈现出双峰结构，而强度为100 PW/cm2的Li3+激光极化方向动量谱表现为在零值附近的尖峰状结构。一般情况下，电离电子的动量是电离时电子的初始动量与激光场驱动电子运动的漂移动量的和，而电子的漂移动量依赖于电离时激光场的矢势，通常认为束缚电子电离时的初始动量很小（可以用一个峰值在0 的高斯分布描述）。如果电子是被激光场越垒电离，则电子的电离率取决于激光场的相位，并在电场峰值附近电离的概率最大，此时的激光场的矢势较小，因此电子末态动量将集中在零动量附近。如果第一次电离的电子有一定的概率返回母离子（通常在场强几乎为零时返回）并与其它电子发生再碰撞后电离，则最后的能量约为2Up，Up=E20/(4ω2)表示电子在激光场中的平均抖动动能。而母离子中的内壳层电子在碰撞后由于能量较低，不能直接电离而被激发到激发态上，等到在下一个场强峰值附近电离而获得了较小的末态动量，因此Li3+的动量分布将会偏离零点。在20 PW/cm2下Li3+离子的双峰状动量分布表明这时的电离过程是再散射导致的非序列三重电离。而100 PW/cm2的Li3+离子的高斯型动量分布表明该强度下的电离的主要通道是序列三重电离。图2（b）与（e）中展示了不同场强下Li3+在激光磁场方向的动量PB的分布，动量谱始终表现为峰值在零点的尖峰状结构。对于激光传播方向k，带电粒子会受到洛伦兹力的作用。因此，Li3+动量峰状结构分布的峰值会轻微偏离零点，如图2（c）和（f）。这是由于在电离过程中对激光场能量的吸收伴随着光子动量的传递，根据式（7），系统会在光场的传播方向额外获得动量。

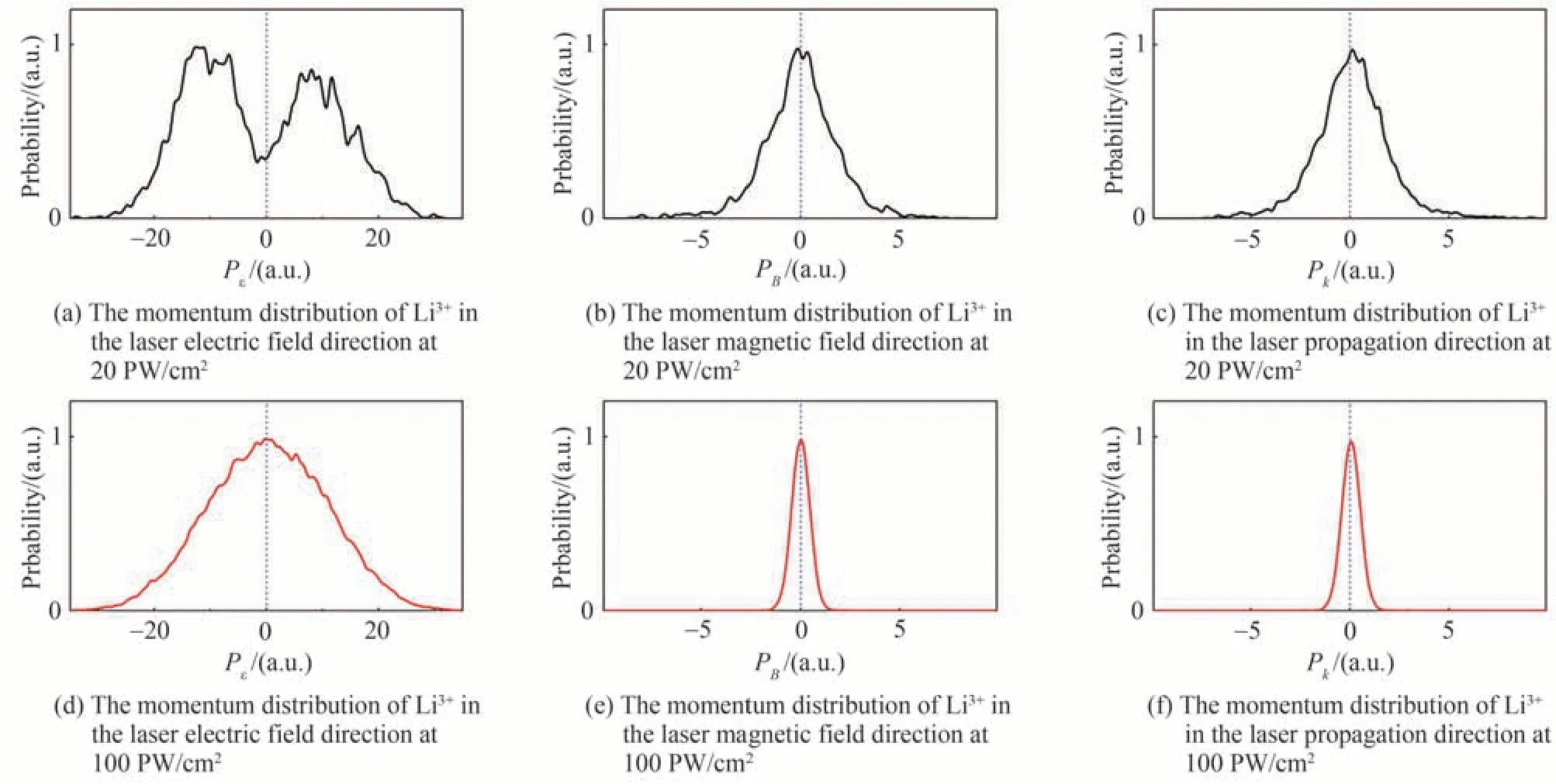
图2 Li3+电离的动量分布Fig.2 The momentum distribution of Li3+

2.3 三重电离的电子能量关联谱

在不同的电离机制下，电子的最终能量分配是不同的。为了进一步研究再碰撞对三重电离的影响，在图3 中利用Dalitz 图［22］的形式描述了不同场强下电子的能量分配。Dalitz 图是通过在等边三角形坐标系上绘制每个电子的相对能量εi来可视化三重电离的完整动力学过程。电子的相对能量定义为εi=Ei/(E1+E2+E3)。如图3 所示，在Dalitz 图中三角形的中心表示三个电子的能量分配相同，而三角形的三个顶点则表示某个电子几乎携带了系统的所有能量。

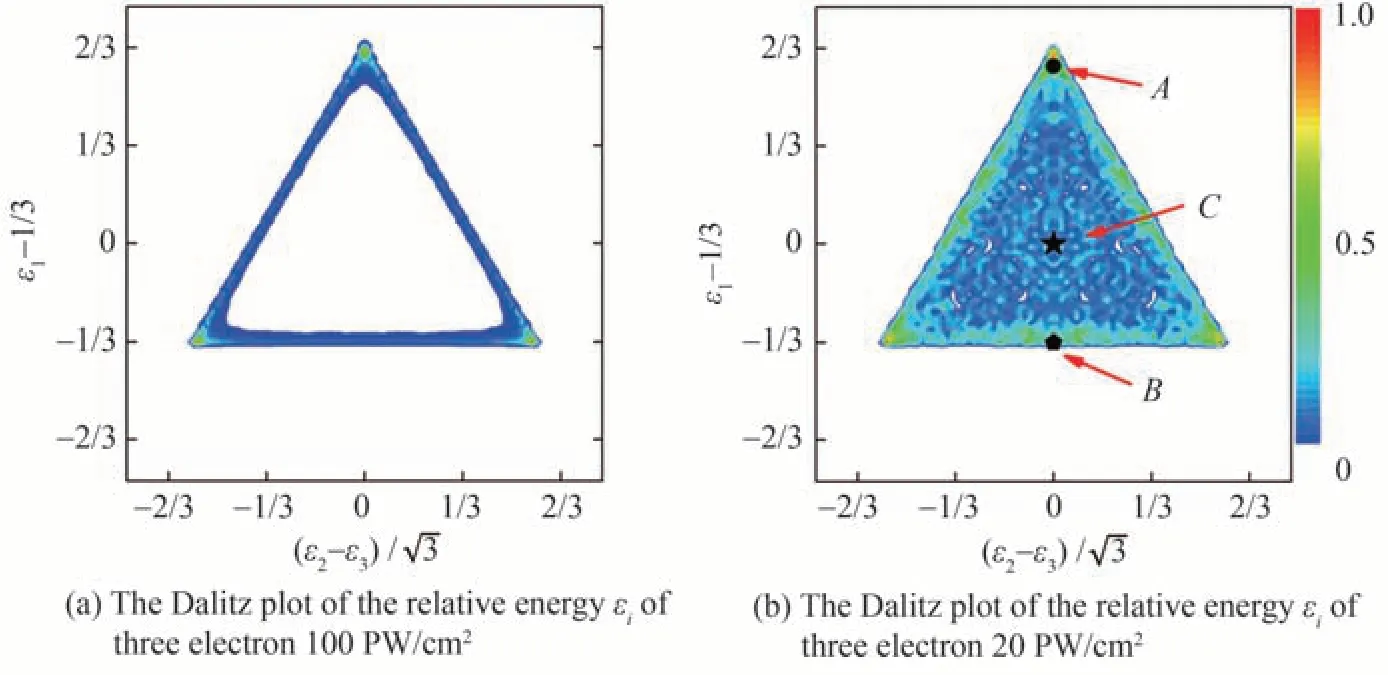
图3 不同激光场强下锂原子三重电离后电离电子的能量分配Fig.3 Energy distribution of ionization electron of lithium triple ionization

当激光强度为100 PW/cm2时，顺序电离占主导地位，即电子一个接一个的被激光场剥离。电离主要发生在激光场振荡的峰值附近，对应的激光矢势接近于0，因此电子的末态能量会接近于0，即分配主要集中在Dalitz 图等边三角形的三条边上，如图3（a）所示。此外，我们看到三角形顶点处的概率分布最大，即某个电子几乎携带了系统所有能量逃逸。通过回溯三重电离的电子经典轨迹，发现这是一类典型电子轨道造成的。图4（a）是这种典型的电子轨道。最外层电子由于较小的电离能，会在激光场上升沿电离且末态能量接近于0。而内壳层电子有一定的概率在场峰值后电离，并在激光场反向后加速返回原子核附近发生散射，使得电子携带远大于其他电子的能量逃逸，但是这种散射是一种软碰撞过程，即电子返回的离核距离大致在十几到几十个a.u.左右。这表明即使在强度高达1017W/cm2的序列三重电离区域也存在电子再散射过程。

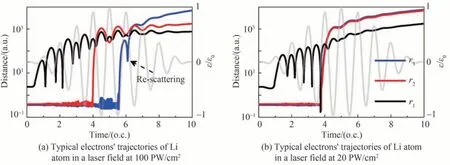
图4 Li 原子三重电离的典型再散射轨迹Fig.4 Typical re-scattering trajectories of lithium triple ionization

图3（b）是20 PW/cm2强度下三重电离电子的能量分布。可以看出电子能量分配更加随机，概率分布弥漫在整个正三角形空间内，Dalitz 图的不同位置对应于不同的电子关联方式。为了揭示背后的物理机制，我们分析了不同强度下发生三重电离的各个电子的电离时间分布发现与序列电离不同，20 PW/cm2强度下的第二次电离和第三次电离的电离时间有明显的重合，通过追溯电子轨道，发现再碰撞过程扮演了重要角色。主要有以下三种电离机制：1）电离的电子被外场驱动返回母离子时，会与其他两个电子发生再碰撞，并通过e-e相互作用将部分能量重新分配给其他两个电子，这两个电子大致在场强为零时被同时电离并在激光场中获得大量能量，这对应于图3（b）中的区域A；2）第一个电离的电子被外场驱动回母离子发生再碰撞时获得了大量的能量，而其他的两个电子几乎同时电离但获得了少许能量，这对应于图3（b）中的区域B；在图3（b）中的区域C 还有一种电离类型，这是清晰的（e，3e）电子关联机制，率先电离的电子返回母离子会被短暂的束缚并与其他两个电子发生热化，最后三个电子大致在场峰值处同时电离，获得能量会大致相同，其典型电子轨迹可参见如图4（b）。

3 结论

本文通过利用Heisenberg 势的量子修正改进了传统的经典轨道蒙特卡罗方法来数值研究了800 nm 线偏振激光场中Li 原子三重电离的再散射过程，在强度约为20 PW/cm2的非序列电离区域，最外层电子在激光脉冲上升沿电离后返回母离子与内壳层的两个电子发生再碰撞并通过e-e相互作用将能量重新随机分配。在强度约为100 PW/cm2的序列电离区域，内壳层电子有一定的概率返回母离子发生弹性散射而获得更高的逃逸能量。

近年来，结合冷原子囚禁技术、强激光脉冲和超快技术建立的磁光阱反冲离子动量谱（Magneto-Optical Trap Recoil Ion Momentum Spectroscopy，MOTRIMS）平台［35］能够将强场多重电离和超快过程研究扩展到碱金属原子。我们揭示的Li 三重电离再散射过程值得进一步关注，这些预测可以通过基于MOTRIMS 的符合测量进行验证。由于碱金属独特的原子结构和超冷的靶温，超冷碱金属原子在高分辨动量谱研究超快飞秒光场诱导的多体相互作用方面有着显著的应用。本文计算模型与模拟结果为飞秒光场中多重电离的精确测量提供了理论参考，同时也为在阿秒尺度上有效操控多个电子提供可借鉴的理论方案。