固体高次谐波：现象、机制及应用（特邀）

吴桐，钱晨，汪子劭，张翔宇，余超，陆瑞锋

（南京理工大学 理学院，南京210094）

0 引言

光与物质相互作用是物理学研究的重要领域，在科学技术的发展中扮演着至关重要的角色。光与物质相互作用的过程，主要通过电子的量子跃迁描述，伴随着光子的发射、吸收或散射。原子、分子、固体等物质的光吸收和光发射现象，正是许多科学技术的基石，例如激光、现代光谱学、X 射线源、光电二极管和太阳能电池等［1］。而激光具有良好的单色性、方向性和相干性，是人们探测物质结构、研究物质性质强有力的工具。自1960年第一台红宝石激光器激光面世［2］以来，得益于调Q 技术、锁模技术、啁啾脉冲放大技术等方面的突破，目前可以获得的激光聚焦功率密度可以达到1022W/cm2［3］，峰值功率达到拍瓦（1015W）量级，激光的脉冲宽度也从纳秒（10-9s）压缩到飞秒（10-15s）量级。随着激光强度不断增强，当激光脉冲的电场强度达到甚至超过原子分子内部库伦势的电场强度时，把激光场看作对电子在原子库伦场约束下运动的微扰观念不再适用，一系列高度非线性的复杂动力学过程也随之出现，如多光子与阈上电离、隧穿电离、非次序双电离和高次谐波产生（High-Harmonic Generation，HHG）。在此背景下，超短超强脉冲的出现逐渐开启了强场物理研究。其中，高次谐波作为一种极有发展潜力的极紫外光源产生方式和实时探测物质内部超快动力学的可能手段，成为强场物理领域中一个备受关注的研究方向。

1 实验进展

1961年，在激光器刚面世不久后，FRANKEN P A 及其合作伙伴就将一束强度约为105V/cm、波长为694.3 nm 的单色光聚焦在石英晶体内从而获得了二次谐波［4］。随后的几十年内，高次谐波的研究主要停留在微扰领域（激光强度通常在108W/cm2左右）。1987年，MCPHERSON A 等使用脉宽为1 ps、中心波长248 nm 的脉冲激光与氖气相互作用，首次观察到了最高17 级次的高次谐波信号［5］。1992年，KRAUSE J L等基于单电子近似，通过求解含时薛定谔方程模拟不同波长的强激光场作用下He 原子和He 离子的高次谐波信号，得到气体谐波截止能量的普适公式：Ecutoff=Ip+3.17Up，其中Ip是电离能，Up是有质动力能［6］。1993年，CORKUM P B 指出原子电离的产物是等离子体的基本成分，强场物理和等离子体物理的关系密不可分，并将等离子物理中的概念应用到强场原子物理中，提出了半经典的三步模型［7］：电子的隧穿电离、电子在强激光场中运动加速以及电子与母核的复合。这一模型非常直观地给出了高次谐波的产生过程并解释了截止频率的存在。近三十年来，基于三步模型的物理图像，气体高次谐波得到了极大的发展，例如分子轨道探测、孤立阿秒脉冲产生、阿秒瞬态吸收等，这都为阿秒物理学奠定了坚实的基础。在气体高次谐波飞速发展的同时，强激光与等离子体相互作用产生的高次谐波由于其高峰值强度、高光子能量和宽光谱宽带的等特点也倍受关注，并且等离子体不用考虑作用媒介的离化阈值，可以承受相对论强度的激光辐照，是产生高品质阿秒脉冲辐射的有效技术途径［8-10］。

虽然气体高次谐波已经被广泛研究并应用到了诸多领域，考虑到气相谐波需要真空泵、真空靶室及相应的约束器件等实验装置来保证严格的真空条件和气体靶材的稳定性，在极紫外光源应用时不易于器件的小型化［11］。固体高次谐波为探索凝聚态体系的电子结构提供了新的途径，同时为了寻找更易集成、更紧凑的极紫外光源，人们逐渐将目光转向固体靶材。固体高次谐波研究实际上也经历了很多年的发展。2001年，CHIN A H 等［12］将中红外激光作用在ZnSe、ZnS、ZnTe、GaAs 等半导体上，观察到了高阶谐波信号。激光峰值强度达到108V/cm 时，由于多光子吸收和隧穿电离引发的材料不可逆损伤和对高能光子的吸收，使得研究者对固体高次谐波的探测受到了极大的限制［13］，而随着可见光、中红外和太赫兹（1012Hz）波段超快激光技术的发展，使得固体靶材可以无损伤地暴露在远远超过其静态介电强度的激光场下，并且使其在该强度的激光作用下可以产生高度可逆的诱导极化，固体领域的高阶非线性光学效应研究得到了极大的发展［14］。2011年，GHIMIRE S 等［13］使用少周期中红外飞秒激光脉冲与ZnO 块状晶体相互作用，观察到非微扰的透射高次谐波。如图1（a）所示，光谱中有明显的平台结构和高达25 阶次截止频率的高次谐波。实验观察到的谐波能量远远超过介质的带隙能量，且与气体高次谐波不同，它的截止频率与驱动激光峰值振幅成线性关系，如图1（b）所示，其中1 Å=0.1 nm，而不是气体高次谐波三步模型预测的与电场振幅的平方成正比。除此以外，固体高次谐波还表现出了不同于气体高次谐波的其他特征，例如，固体高次谐波对晶体取向的依赖性，不同取向的高次谐波光谱可能会出现偶次谐波信号，如图1（c）所示。同时，低阶的固体谐波信号对于激光的椭偏率并不敏感。因此固体高次谐波既不能通过传统的微扰非线性光学描述，也不能通过简单的三步模型来解释。他们认为该实验中的高次谐波来源于隧穿电子的布洛赫振荡（Bloch oscillation）。基于这一物理图像，可以得到截止能量和驱动激光峰值电场大小呈线性关系。

图1 ZnO 晶体的高次谐波实验结果［13］Fig.1 Experimental data of HHG from ZnO crystal［13］

自从ZnO 晶体的非微扰高次谐波信号被观察到以后，研究者们［15-43］也相继从其他块状晶体［15-18，20-22，38-41］、稀有气体固体［23］、单层材料［24-27］、纳米结构［19，28-29，43］、非晶固体［30］、掺杂体系［31，42］和拓扑绝缘体［32-33］等体系中观测到高次谐波信号。此外，基于固体靶材产生的高次谐波在新型紧凑阿秒光源［19，28-29，33-34］、探测能带结构［21，35-36］、贝里曲率［21，25］和拓扑效应［32-33，37］等领域也有令人惊喜的突破。本章节着重叙述固体高次谐波研究在实验方面的进展。

2014年，SCHUBERT O 等［15］研究了GaSe 在太赫兹场驱动下的高次谐波辐射过程，并比较了不同载波包络相位（Carrier Envelope Phase，CEP）下的谐波信号，他们认为带内的布洛赫振荡结合相干的带间激发是高次谐波产生的原因，通过改变驱动激光场可以实现载流子不同电离路径间的量子相干。2015年，HOHENLEUTNER M 等［38］利用强太赫兹激光脉冲作用在GaSe 上，在时域上得到高次谐波信号，发现高次谐波光谱是由一系列亚周期的谐波发射构成，并在时域上与驱动激光的波峰相一致，证明多个能带间电子带间跃迁的非微扰量子干涉在高次谐波辐射中起着重要作用。与此同时，LUU T T 等［21］利用少周期的强激光作用在120 nm 厚的SiO2薄片上（实验装置如图2（a）所示），得到了高达40 eV 的紫外辐射（图2（b）），并通过理论计算与实验数据对比，发现谐波信号主要来源于带内电流。同一年，VAMPA G 等［16］利用0.25×108V/cm 的中红外激光作用在ZnO 晶体上，并用一束非常弱的二次谐波去扰动这个过程，通过改变两束光之间的相位差成功调制奇偶谐波的强度和相位，他们类比气相原子、分子的高次谐波产生过程，提出广义的电子-空穴碰撞模型，并用此解释了双色场调制下的ZnO 高次谐波光谱，同时指出能带色散关系和退相过程是影响谐波信号的重要因素。

图2 SiO2薄膜产生相干EUV 辐射的实验装置和高次谐波谱［21］Fig.2 Experimental setup for coherent extreme ultraviolet（EUV）radiation from SiO2 thin film and the measured high-harmonic spectra［21］

2016年，LANGER F 等［39］利用飞秒激光作用在层状WSe2上，得到了22 阶的高次谐波，并通过全量子的计算拟合，认为高阶光谱的带边激发以及准粒子碰撞、湮灭、相干、退相干的动力学过程是高次谐波产生的主要机制。2017年，WANG Z 等［40］通过泵浦-探测实验在时域上控制注入的光载流子，成功识别了不同级次高次谐波的带内和带间跃迁的贡献，证明了在强中红外激光脉冲的驱动下，带间跃迁在ZnO 晶体的带隙以下和带隙以上的高次谐波发射中的重要作用。同一年，YOU Y S 等［17］成功探测到MgO 的高次谐波信号，发现线偏光的极化方向沿着Mg-O 键方向即晶体的＜100＞方向时，高次谐波信号有极大的增强。他们还发现，MgO 的高次谐波信号对驱动激光的椭偏率有很强的依赖性，并通过半经典轨迹模拟，证明了原子间的相互作用和近邻原子的散射效应对高次谐波信号的影响。随后，YOU Y S 等［30］对非晶熔融SiO2的高次谐波信号进行了测量，说明周期性结构并不是产生相干XUV（Extreme Ultraviolet）的必要条件，同时谐波信号对CEP 的强依赖性说明了谐波信号与驱动激光的锁相机制。2018年，SCHLAEPFER F 等［41］利用阿秒瞬态吸收光谱来探测GaAs 对近红外激光的响应，实验表明半导体对共振泵浦激发的早期响应主要来源于电子的带内运动，而带间极化和带内运动的耦合明显增强了载流子从价带注入到导带这一过程。

2019年，HAN S 等［20］在研究蓝宝石高次谐波的实验中，通过测量角度依赖的高次谐波谱，成功提取出了材料取向依赖的高阶非线性极化率，并强调了带间跃迁对高次谐波产生的重要性。同一年，YANG Y 等［42］利用近零介电常数材料产生了高达9 阶的高次谐波信号。他们将波长为2 080 nm、脉冲宽度为60 fs 的激光以一定的角度掠入射到75 nm 厚的In 掺杂CdO 薄膜上，探测到了高次谐波信号有明显的光谱红移和谱线展宽，并将其归因于材料中导带电子的光致发热和相应的随时间变化的近零介电常数。2020年，VAMPA G 等［18］利用强近红外激光与200 μm 厚的MgO 晶体相互作用，用双色场研究产生的XUV 波段高次谐波信号，发现反射谐波的双色光谱与广义的电子-空穴复碰撞模型相吻合，而透射谐波的双色光谱则被明显调制，并将其归因于传播效应对透射信号的影响。

研究者们对于固体高次谐波的研究并没有局限于传统的半导体和绝缘体靶材。2016年，NDABASHIMIYE G 等［23］发现稀有气体固体（Ar、Kr）的高次谐波谱呈现多个平台结构。他们用波长为1 333 nm 的驱动激光聚焦在固体氩上产生高次谐波辐射，在中等峰值强度的激光激发下，截止位置平滑增加，直到27 次谐波。当激光的峰值强度增强到20 TW/cm2左右时，光谱截止位置突然增加到35 次谐波。第一个平台区域在所有强度上都比第二个平台区域要亮，如图3（a）所示。通过与气体高次谐波的对比，表明了周期性势能的影响，也说明多能带耦合、电子-空穴对的复合对于固体谐波产生的重要性。通过求解含时薛定谔方程的理论结果如图3（b）所示。稀有气体固体是连接原子高次谐波和固体高次谐波的桥梁，对于研究固体谐波和气体谐波的机制有重要的参考意义。

图3 固体Ar 的高次谐波谱［23］Fig.3 High-harmonic spectra from solid Ar［23］

二维材料，由于其独特的结构、优越的光电性能备受关注。同时，二维材料由于电子运动的空间约束以及谷、轨道、自旋、转角等多种自由度之间的相互耦合，使其具有独特的量子效应与性质。二维材料的高次谐波辐射等非线性光学响应也引起研究者们的注意。2017年，YOSHIKAWA N 等［24］利用中红外（mid-infrared，MIR）激光脉冲激发石墨烯，观测到高达9阶的高次谐波信号，并发现石墨烯的高次谐波信号在椭圆偏振的激光激发下得到增强，产生的高次谐波具有反常的椭偏依赖。2017年，斯坦福大学的LIU H 等［25］探测到了单层MoS2在中红外激光驱动下谐波信号可以扩展到13 阶。他们分析了平行和垂直于基频场的谐波辐射分量随晶体取向的变化，如图4（a）（c）所示。他们改变泵浦激光与晶体镜像平面之间的夹角，分别测量得到高次谐波信号的垂直和平行分量随之变化的规律，如图4（b）（d）所示。他们发现垂直分量只有偶次谐波信号，并且其强度以60°为周期变化，而平行分量上探测到的奇偶次谐波信号，同样表现出了6 重旋转周期性，但是相比于垂直分量，谐波的强度极值平移了30°。他们将高次谐波谱展现出的这些特性归因于晶体的对称性，说明了对称性破缺和贝利曲率对于垂直于激光极化方向的偶次谐波的增强效应。2018年，HAFEZ H A 等［26］利用峰值电场强度为12～85 kV/cm、中心频率为0.3～0.68 THz的激光作用在石墨烯上，观察到石墨烯能非常高效地产生太赫兹波段的高次谐波，并指出狄拉克电子对驱动太赫兹场的集体热响应是产生这一现象的关键。与此同时，YOSHIKAWA N 等［27］对四种单层过渡金属硫化物材料（MoSe2，MoS2，WSe2，WS2）的高次谐波信号进行探测，他们将偶次谐波的增强归因于能带嵌套结构之间的共振，而谷动力学的不对称性和各向异性的能带结构导致了高次谐波的极化，并强调非线性带间极化对固体中的高次谐波产生有重要的贡献。二维材料表现出的独特的非线性响应现象，为人们进一步理解光与物质的相互作用提供了新机遇。

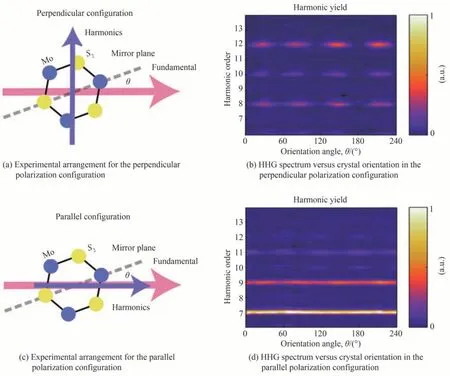
图4 单层MoS2晶体取向依赖的高次谐波谱［25］Fig.4 Crystallographic orientation dependent harmonic spectra frommonolayer MoS2［25］

固体高次谐波在纳米结构方面的发展为超快电子学、超高频率电子信号处理器件的设计提供了基础，也为实现新型极紫外光源提供了思路。2016年，HAN S 等［28］设计了一个金属-蓝宝石纳米结构，该纳米结构是一种三维锥形波导，波导结构如图5（a）（b）所示，通过表面等离子体极化激元（Surface Plasmon Polaritons，SPPs）在蓝宝石尖端沿金属-蓝宝石界面增强电场，在强度为0.1 TW/cm2的飞秒脉冲作用下产生了60 nm 的极紫外奇次谐波信号，如图5（c）所示。2017年，VAMPA G 等［19］使用中心波长为2 100 nm 的红外飞秒激光脉冲聚焦在500 nm 厚硅薄膜上的金纳米棒天线阵列，观察到了在等离子体场增强辅助下产生的非微扰高次谐波，他们发现平行于硅薄膜［100］方向的阵列的高次谐波信号弱于平行于［110］方向。通过与没有天线阵列的块体Si 的谐波信号相比较，尽管表面天线覆盖稀疏，但谐波辐射比没有天线时要强10 倍。同年，SIVIS M 等［29］利用ZnO 表面突出的锥状、楔形的纳米结构和离子注入硅形成菲涅尔圆盘来限制驱动激光场，增强了谐波发射信号。他们发现ZnO 表面的锥状光栅导致锥壁上的全反射局部增强场，最终在光栅尖处的聚光区形成高次谐波的增强发射，并指出在远场处的衍射图样来源于3、5 阶谐波的空间干涉。同时，他们还通过ZnO 表面平行的楔形光栅得到了衍射角分辨的高次谐波谱，发现沿着光栅顶端的发射增强。除此之外，他们通过在硅样品内注入镓离子形成菲涅尔圆盘的图样，证明了高次谐波的增强发射来源于镓注入的区域。他们指出，通过改变固体的化学成分和形貌，可以局部地定制高次谐波的产生介质和驱动场。2018年，LIU H 等在［43］225 nm 厚的单晶硅薄膜上制备了由条形天线和圆盘谐振器组成的周期性结构单元，并形成Si的超表面结构。这种结构构成了典型的三能级法诺共振系统，导致出现类似于经典的电磁波诱导透明现象。他们利用2 320 nm、70 fs的激光聚焦在该器件上，观测到了高次谐波信号。他们发现，与没有图样的样品相比，谐波发射的强度增加了两个数量级以上，且增强的高次谐波由于共振特性而具有激发波长的选择性。因此，随着电子工程技术和纳米工程技术的发展，固体高次谐波的空间分布、强度和相位有望实现进一步调控。

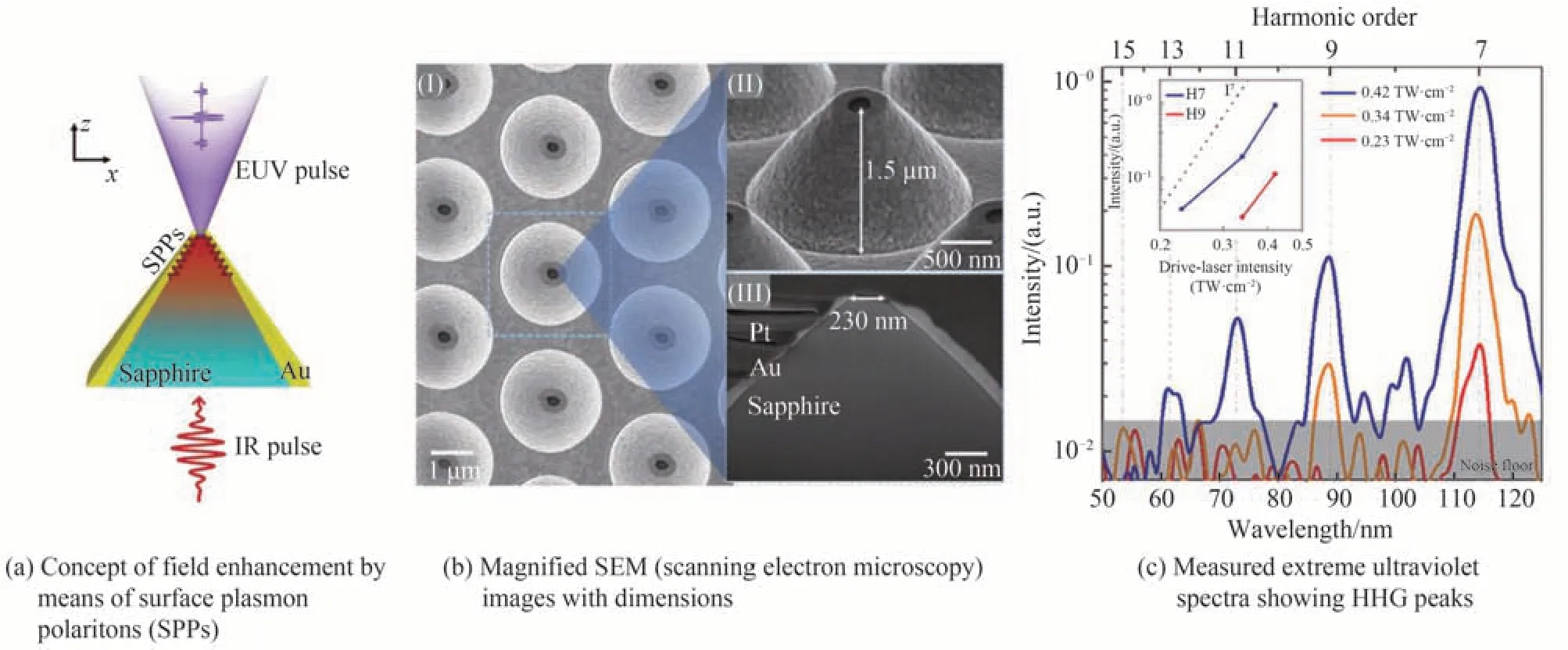
图5 金属-蓝宝石纳米结构及其高次谐波光谱［28］Fig.5 Fabrication of the metal-sapphire nanostructure and the measured high harmonic spectra［28］

拓扑绝缘体具有丰富且有趣的电子态特征，利用全光学手段来探测其本征载流子的输运问题有望观测到不同于普通半导体材料的现象。近期，对拓扑材料的高次谐波实验方兴未艾，研究从一维的拓扑链到三维拓扑材料的表面态或体态电子结构不断展开。固体高次谐波为探究拓扑绝缘体和拓扑表面态提供了新的途径。2018年，SILVA R E F 等［44］利用高次谐波的螺旋度的反转实现了Haldane 模型的拓扑相变表征，推动了利用全光学探测拓扑相变的可能。2021年，BAI Y 等［32］在本征拓扑绝缘体BiSbTeSe2中，观察到了表面态电流和光场引起的非平衡表面自旋流，这两者分别是通过打破体系表面的空间反演对称性和时间反演对称性引起的，并证明了偶次谐波可以表征拓扑表面态上被强场驱动的螺旋狄拉克费米子。而BAYKUSHEVA D 等［45］从理论上阐明了强场驱动的高谐波辐射对能带结构拓扑以及自旋轨道相互作用表现的敏感性，并且在他们后续的实验工作中得到验证［46］，实现了基于圆偏振激光器驱动的三维拓扑绝缘体的高次谐波的反常椭偏依赖。SCHMID C P 等［33］也在实验上观察到了拓扑绝缘体材料Bi2Te3在太赫兹场驱动下的高次谐波信号，发现在体态和拓扑表面态产生谐波辐射有明显的区别。他们指出，Bi2Te3表面的非整数阶高次谐波辐射是由体系非平庸的表面狄拉克费米子在强激光诱导下群速度的突然反向引起的，是线形色散的电子态能够产生高阶非线性光学现象的证明。

固体高次谐波现象为人们探索光与物质相互作用的微观动力学过程提供了全新的手段。在气体高次谐波领域，早有利用高次谐波信号探测分子轨道和动力学信息的实验被报道。2006年，BAKER S 等［47］通过高次谐波谱探测了氢分子和氘分子离子中的核运动信息。2010年，HAESSLER S 等［48］也成功利用谐波信号重构了N2的HOMO 和HOMO-1 轨道。而在带内布洛赫振荡的模型下，固体高次谐波的产率和能带色散关系直接关联，因此，固体高次谐波可为测量晶体电子的色散关系提供新的途径。2015年，LUU T T 等［21］成功从SiO2高次谐波谱中重构出晶体的导带结构。同年，VAMPA G 等［35］也通过高次谐波的带间发射机制和双色场技术重构了ZnO 的能带结构。他们利用一束弱的二阶谐波去扰动高次谐波的产生过程，产生了偶次谐波光谱，如图6（a）所示。然后提取不同阶次谐波信号中被二次谐波调制后的相位Φosc，如图6（b）所示。采用许多组不同能带带隙来模拟计算得出Φosc并与实验比较，最后找到与实验得到的Φosc吻合最好的一组能带，从而实现能带重构，如图6（c）所示。2017年，LANIN A A 等［49］通过高次谐波强度和驱动激光强度的关系，利用带内谐波模型拟合色散关系傅里叶变换后的系数，成功重构了ZnSe 的电子能带结构。2020年，UZAN A J 等［36］引入动态联合态密度并确定其与光谱的映射关系，成功探测了多个未占据的导带结构。高次谐波光谱技术拥有高的光子能量与高精度的时空分辨能力，可探究物质结构和性质在外场影响下的动态变化，将成为扫描隧道显微镜、电子衍射和角分辨光电子能谱等实验技术之外的一项重要光学方案。

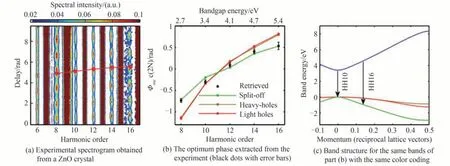
图6 固体高次谐波用于能带重构［35］Fig.6 Reconstruction of the energyband by means of HHG-solid［35］

利用带内电流模型，同样可以获取晶体的贝利曲率和贝利相位。2017年，LIU H 等［25］将MoS2的谐波信号垂直分量角分辨图谱与贝利曲率相联系。2018年，LUU T T 等［50］成功通过高次谐波信号重构了SiO2的贝利曲率。除此以外，利用高次谐波信号重构电子势能曲线、探测电荷分布方面也有所突破。2020年，LAKHOTIA H 等［51］利用高次谐波信号成功实现了皮米（picometre）尺度分辨的价电子成像。基于散射理论，他们证明晶体最小原子和离子半径的尺寸与高次谐波信号截止能量之间的直接联系，同时得到了平行于激光偏振方向高次谐波的强度和相应晶体周期势能之间的关系，并成功重构了MgF2和GaF2价带电子势和价电子密度。当激光偏振矢量分别与［110］和［100］轴一致时，重构的价带势能一维截面（蓝色曲线）如图7（a）（b）所示。灰色和橙色的球体分别代表F-和Mg2+离子。基于图7（a）（b）中的数据，以及沿晶体［120］方向测量的数据，他们重构了MgF2晶体（001）平面的电位，如图7（c）所示。对固体价电子的超快时间分辨成像拓展了现代原子尺度显微镜的范围，为固体的电子性质、化学性质、拓扑性质的直接探测提供了新的可能。

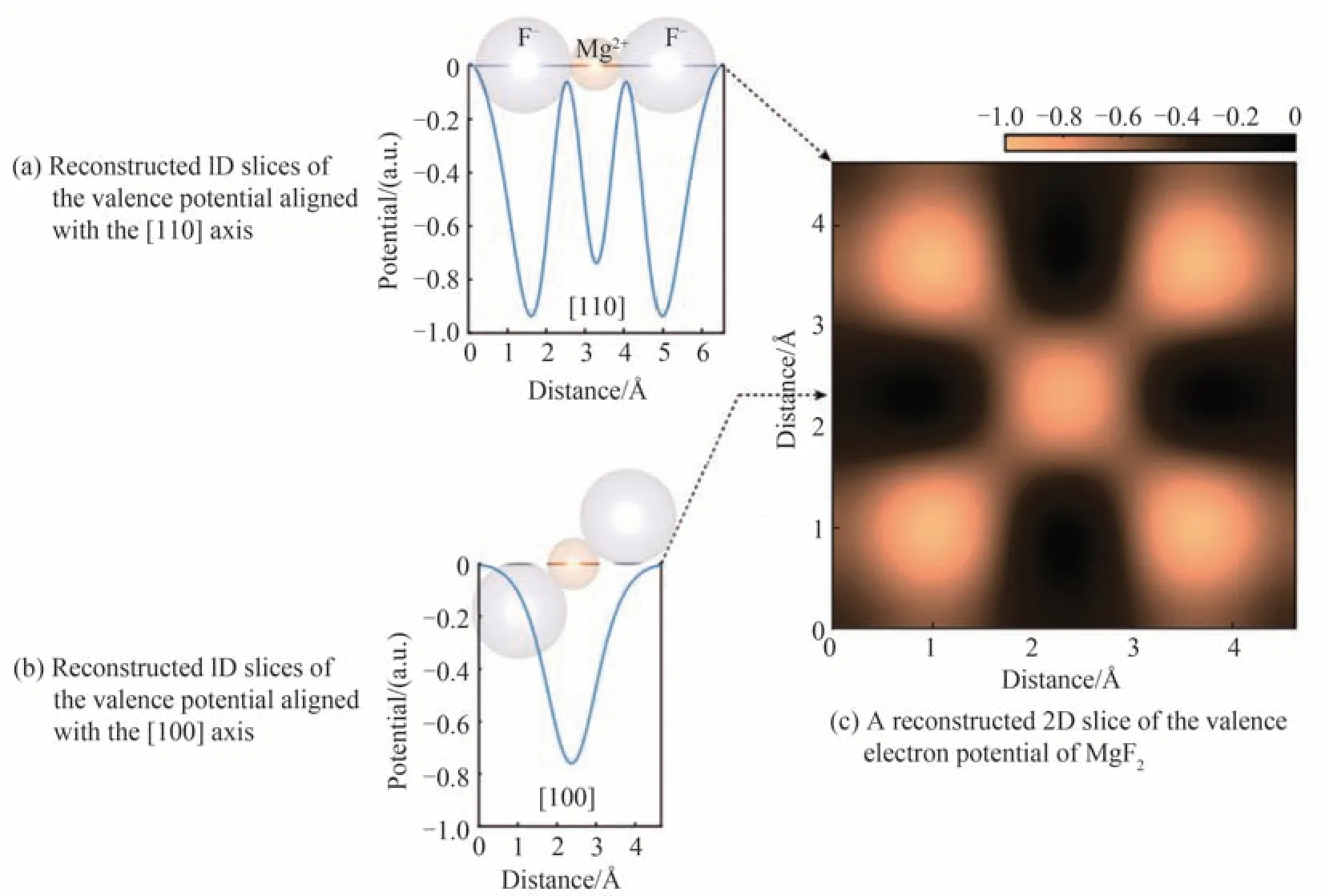
图7 MgF2价带电子势和电子密度的重构［51］Fig.7 Reconstruction of the valence electron potential and density of MgF2［51］

从上述一系列实验中可以发现，人们对固体高次谐波的探索是螺旋上升、波折前进的，仍存在许多争议和未解之处。总的来说，固体对强激光场的响应受到许多因素的共同影响，固体中高次谐波的产生可以归因于总电流的带间和带内分量，而它们的相对贡献大小强烈地依赖于材料固有特性、驱动激光参数以及所观测谐波的光谱范围。

2 理论进展

关于固体高次谐波的理论研究可以追溯至上个世纪90年代［52］。迄今为止涌现出许多优秀的理论工作，为实验观测、分析与预测提供了坚实的理论基础。本章节总结了固体高次谐波相关的理论数值方法和理论研究成果，并着重探讨固体高次谐波的理论机制。

2.1 Keldysh 理论

物质对光的吸收和辐射过程往往伴随着电子的跃迁。对于光强较弱的激发过程，电子的跃迁可以基于静态哈密顿量构建的基组，通过微扰理论进行计算。当激光强度足够大时，微扰理论失效。1965年，KELDYSH L V 提出了描述原子和电介质在强电磁场作用下非线性电离行为的理论，即Keldysh 理论（也被称为Keldysh 模型）［53］，他假设电子的初态由不受激光场扰动的波函数Ψ0(r)=ψ0(r)exp(iIpt/ℏ)描述，其中ψ0(r)是原子势场下的基态波函数，Ip是电离能；而末态Ψp则仅考虑光场和电子的相互作用，忽视母核离子的库仑力对其的影响，由对应于电子正则动量p的Volkov 函数得到。基于此，可以得到原子的束缚态和光电子动量为p的连续态之间的跃迁概率振幅：M(p)=-其中Vint是电子和场的相互作用算符［142］。有许多相关的工作继续完善和拓展这一理论，并在它的基础上发展出来一系列经典和量子力学的研究方法。这一理论在气体高次谐波领域，发展出了强场近似理论［54-55］（Strong-Field Approximation，SFA）。将此推广到固体材料的光激发研究中，忽略被激发到导带的电子与遗留在价带的空穴之间的相互作用，可以通过Keldysh 参数来判断带间跃迁的过程［56］

式中，Eg是带隙，Up是有质动能。如果γ≪1，那么光激发电子跃迁过程可用隧穿机制来解释，这一过程是近似绝热的；如果γ≈1，电子跃迁过程则是非绝热的［57］，多光子跃迁和隧穿跃迁相互竞争，过程变得更加复杂；γ≫1，多光子激发占主导地位。Keldysh 理论对于探讨高次谐波产生过程中的跃迁行为有非常重要的意义，也对我们选择合适的模型处理实际问题有指导作用。

2.2 广义“三步模型”

气相原子的高次谐波辐射可以通过一个半经典的“三步模型”［7］来描述，包括隧穿电离、电子在电场中的加速和电子与母核的复碰撞，如图8（a）所示。晶体材料具有周期性的晶格结构、更高的原子和电子密度，相邻原子之间耦合更强，使得固体高次谐波的物理图像更为复杂，需要对周期性势中的电子动力学建立新的模型。对周期性势场中的粒子的成功描述，是量子力学最伟大的成就之一，固体能带理论在此基础上被逐渐完善。

在固体能带理论框架中，光激发晶体材料产生电子-空穴对，从而诱导材料的光电特性。基于Bloch 定理，使得我们可以在动量空间中更加便利地分析周期势场下载流子的运动。因此，类比原子高次谐波的“三步模型”［7］，固体高次谐波的产生机制主要是通过动量空间中的广义“三步模型”进行解释［11，58-59］，图8（d）所示。考虑两能带模型，在强激光场的作用下，价带电子通过多光子过程或者Zener 隧穿［60］（Zener tunneling）跃迁到导带。根据Houston 绘景［61］，电子的准动量可以表示为：k(t)=k0+A(t)，电子的晶格动量随着驱动激光的矢势含时变化，这导致载流子在非抛物线型的能带中运动，电子的有效质量随k(t)变化，因此激光场驱动下的电子沿能带的运动是非谐的，这会导致非微扰的带内谐波发射。电子在激光的驱动下会有一定的概率从价带跃迁到导带，形成电子-空穴对，电子在导带上运动的过程中随时可能和空穴复合，释放出高能光子，其中高能光子的频率和瞬时的带隙相对应，这就是高次谐波产生的带间机制。如今，两能带模型也已经拓展到多能带模型，带间极化和带内电流之间的干涉和耦合对高次谐波的产生有十分重要的影响［41，105］。在动量空间中，空穴和电子的位置始终一一对应。在实空间中，固体高次谐波的“三步模型”［11，62-63］仍然为：电子隧穿产生电子-空穴对；电子和空穴在空间加速分离导致带内发射；电子和空穴在空间中再次相遇复合产生带间发射，如图8（c）所示。最近，LI L 和SONG X 等相继提出了固体高次谐波的四步模型［64-65］，他们认为固体中价带电子在发生隧穿激发之前存在预加速过程。YUE L 等［66-67］对广义三步模型的隧穿和复碰撞过程采用多种模型分析，认为谐波发射的主要来源并不是最小带隙处的隧穿，而是由于布里渊区不同对称点附近隧穿区域的集体效应，导致不同的谐波能量和发射分布。同时他们还指出，非完美复碰撞过程（电子-空穴在空间上并没有完全重合）对于单层和块体材料都非常重要。可见，固体高次谐波的理论模型仍然有探讨和完善的空间。

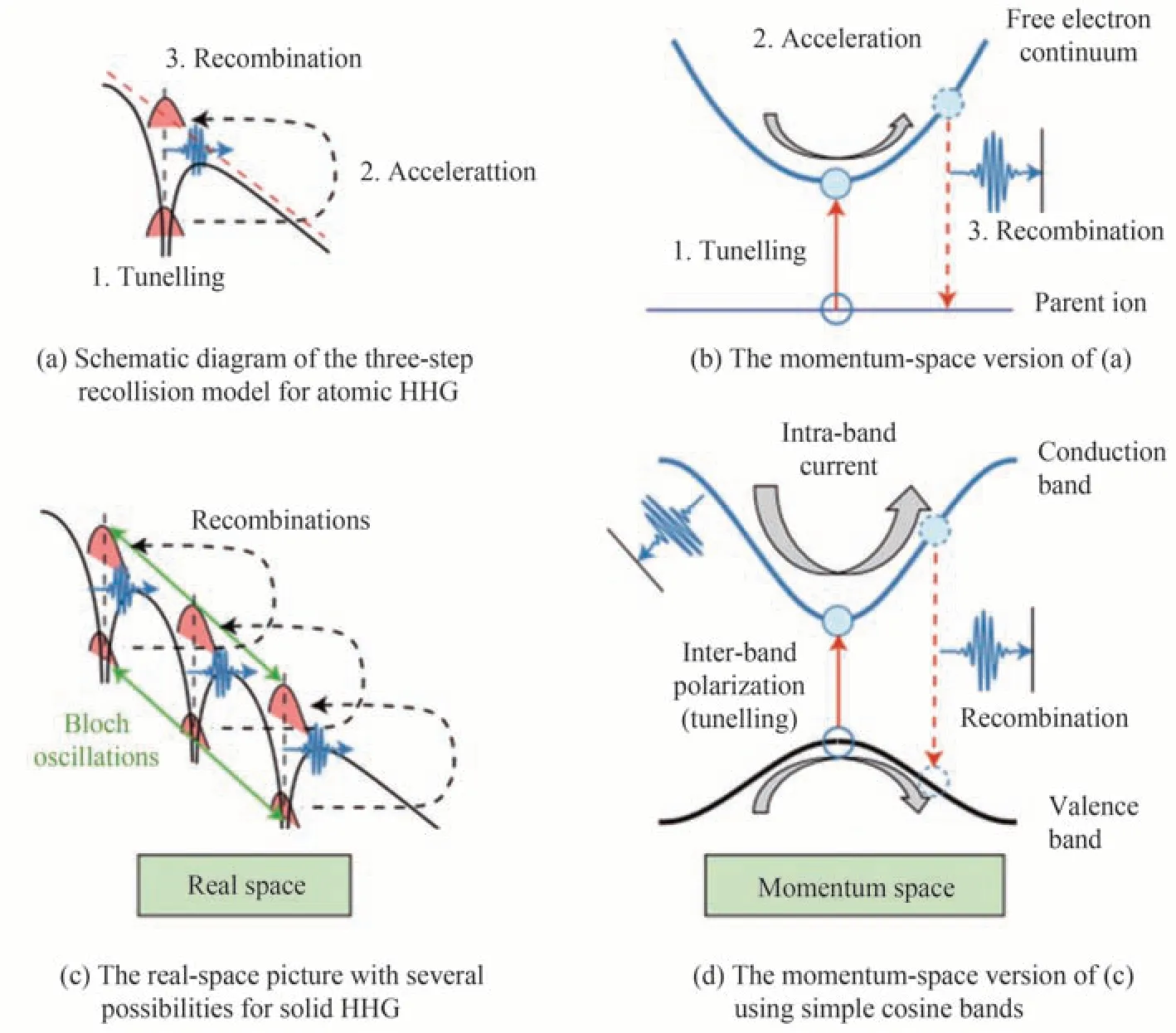
图8 原子和固体高次谐波产生的微观机制［11］Fig.8 Microscopic mechanisms for atomic and solid-state HHG［11］

在强场条件下，带间极化和带内布洛赫振荡是紧密耦合的，固体高次谐波中很多独特的现象都与这两种机制有关。GOLDE D 等［68］通过理论计算证明了带内电流的存在对带间机制产生的谐波有影响。和带间机制相比，带内发射基本和激光场的相位同步［69］。而带间图像则成功解释了包含啁啾的高次谐波信号［16，18］，啁啾的产生取决于激光参数和能带结构，同时传播效应还能通过激光脉冲的色散［70］和自相位调制增加额外的啁啾。理论和实验表明，带间和带内分量都可以产生低于和高于晶体带隙的高次谐波信号，带间和带内分量都具有截止频率随激光电场峰值强度线性变化的特征［13，21，35，38］，且与电子能带结构密切相关。根据带间模型，截止能量受能带间最大带隙的限制［35，69］。当被驱动的电子获得足够的能量爬升到更高的导带时，有望出现一个新的平台和截止能量［71］。在带内模型中，不存在带隙极限［13，21，68］。然而，对于足够强的驱动激光场，电子仍然可以隧穿到高导带［11，60］。这也阻碍了对主要贡献的明确识别，因此真正区分两者的贡献仍有许多问题亟待解决。带内或带间成分是否会在实验中主导高次谐波的产生，主要取决于所研究的材料、所采用的激光参数以及发射的谐波能量。

2.2.1 带内机制和布洛赫振荡

电子或空穴在每个光周期内不断重复的布洛赫振荡是强太赫兹场下产生高次谐波信号的潜在机制之一［13，21］。这一机制得到了诸多实验和理论的验证［15，17，22］。

在激光场的驱动下，一旦外场将电子驱动到布里渊区边界，电子的德布罗意波长就等于晶格周期的两倍

此时，电子将在布里渊区边界发生布拉格散射。在简约布里渊区中，电子的运动轨迹终止于第一布里渊区边界，并在对应的另一侧穿出。如果电子被限制在一个特定能带内，并且在每半个光周期内周期性穿越布里渊区，那么我们就称电子进行布洛赫振荡。如果忽略晶体中声子、杂质、缺陷等引起的散射效应，振荡的峰值频率为ωB=eE0a/ℏ［13］，电子的加速度和群速度表示为为［72］

式中，F(t)是激光场的振幅，E(K)是能带色散关系。如图所示。一般情况下，E(k)可通过傅里叶变换展开为［21］E(k)=2其中，a是晶格常数，n是谐波的阶数，nmax是描述能带色散关系且满足精度要求的最高阶数，ϵn是傅里叶变换的系数。在此表述下，电子或空穴在带内能运动的最大特征距离为Rmax=nmaxa，从而电子或者空穴在外场中可以获取的最大能量为Emax=eE0Rmax=nmaxℏωB。第N阶谐波的强度和频率为ωL的驱动电场的关系为［21］

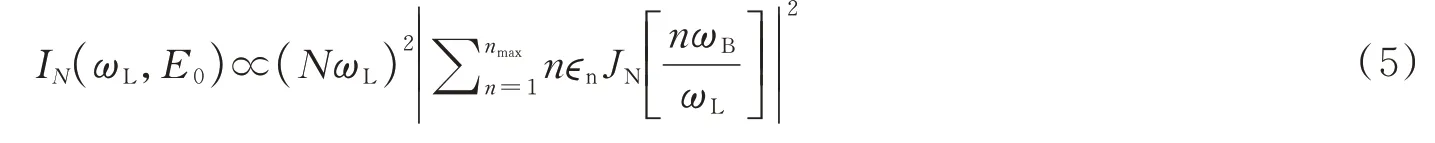
式中，JN是贝塞尔函数。

因此，带间高次谐波的截止能量和截止频率分别表示为［21］

结果表明，带内图像能够再现固体高次谐波发射对载波包络相位的弱敏感性［21-22，34］，并能合理解释高次谐波谱的平台结构以及截止能量和驱动激光峰值电场强度的线性关系［13，71］。如上一章节所提到的，带内电流和能带色散关系的联系，是通过谐波信号重构能带的重要依据［21，49］，而从时频分析上看，带内谐波发射主要发生在激光场的峰值强度处［69］。

2.2.2 带间机制

带间机制和广义“三步模型”成功解释了固体高次谐波的啁啾发射——谐波的发射时间随谐波阶数的变化而变化，并且与驱动场波峰不同步［16，18］。根据VAMPA G 等的预测，由于带间跃迁的存在，带间谐波的最大截止能量受不同能带间最大跃迁能量的限制，并且与激光场的峰值强度成线性关系［73］。由于固体中有多个能带存在，并且电子可以通过在导带间的逐步跃迁爬升到更高的能级［23，36，74-75］，因此两能级系统并不能完备地描述固体高次谐波。如果电子被激发到能量更高的能带，截止能量就将得到扩展，并在光谱中表现出第二个平台区［69，74-75］。直接带间跃迁及由于多个价带和导带的存在而产生的多跃迁通道干涉［38，71，75-76］丰富了固体高次谐波的带间机制。最近，二维半导体中红外高次谐波实验的准经典分析也指出了带间机制对最小带隙能量以上谐波的重要性［27］。

2.2.3 贝利曲率和贝利相位

自从发现贝利相位以来，它的概念已经几乎渗透到物理学的所有分支。在过去的三十年中，人们逐渐认识到电子波函数的贝利相位可以对材料的物理性质产生深远的影响，并与一系列现象紧密相关，如极化、轨道磁性、量子（反常或自旋）霍尔效应和量子电荷泵浦［77］。当一个用描述的量子系统，在由一组绝热参数R(t)=[R1(t)，R2(t)，…]构成的参数空间中沿着封闭的环形路径C绝热演化，那么在它回到初始位置R(t0)时，除了会累积一个固有的动力学相位-iEnt/ℏ 外，还会获得一个几何相位γn(C)，此时几何相位是参数空间中一个闭合回路的线积分，这个几何相位就是贝利相位［77-78］，相应的路径积分为

式中，被积函数An(R)就是贝利联络，是一个向量，维度和参数空间的维度相同，一般定义为

式中，S(C)表示路径C所围成的曲面，而贝利曲率就是面积分中的被积函数

值得注意的是，贝利联络是依赖于规范选取的，如果对基函数做规范变换那么贝利联络会变为An(R)→An(R)-∇Rζ(R)。因此，可以得到系统因绝热演化累积的相位改变量为ζ(R(t0))-ζ(R(t) )；长期以来，人们认为这种由波函数在绝热演化过程中积累的相位因子在物理上是没有意义的，似乎总可以通过规范变换使得该相位变为0［56，77-79］。直至1984年BERRY M V 指出［80］，在该参数空间中，只有R(t)的路径保持开放时，相位因子是可以通过规范变换消除的；但如果路径封闭，即返回到起始点R(t0)，这就意味着R(t)=R(t0)。此时再进行规范变换，那么ζ(R(t0))-ζ(R(t) )必须等于0或者2π 的整数倍，那么累积的相位变化是规范不变的，因此呈现一个物理可观测值。贝利曲率与晶格对称性有紧密的联系。倘若系统具有中心反演对称性，那么Ωn(k)=Ωn(-k)；倘若晶格具有时间反演对称性，则Ωn(k)=-Ωn(-k)；倘若晶格同时具有中心对称性和时间反演对称性，那么Ωn(k)=0。如果贝利曲率不为0，那么在没有磁场的情况下，被电场驱动的波包将会获得一个额外的速度分量，即反常速度［77］

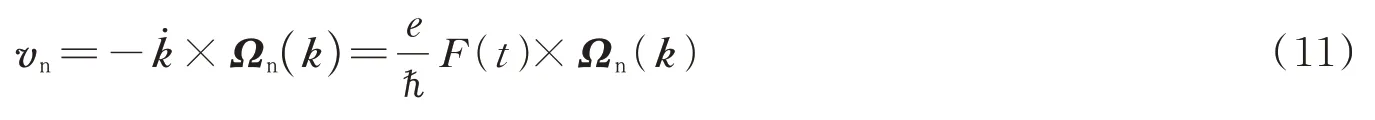
在不考虑磁场的情况下，反常速度与电场正交。几乎所有的物理和化学过程都受到选择定则的支配，而选择定则是对称原理的直接体现［81］。贝利曲率对固体性质的影响，本质上也是对称原理的直接体现。纯奇次谐波是中心反演对称体系和具有C2对称性的驱动光相互作用的结果［82］。固体中空间反演对称破缺导致Berry 曲率在动量空间中不再是偶函数［77］，这是固体中垂直于激光极化方向上偶次谐波辐射的可能原因之一［25］。此外，空间对称性的破缺也可能导致平行方向上偶次谐波出现，这是由于非中心反演对称的体系中位移矢量的作用［83］。

如上文所述，LIU H 等认为贝利曲率导致的反常速度分量是MoS2产生垂直于激光偏振方向的偶次谐波信号的原因［25］。而LUUTT 等在后续的实验中通过高次谐波信号成功重构了SiO2的贝利曲率［50］，如图9（b）所示。为了重构贝利曲率，他们将晶体定向到Γ-M 方向，并且线偏激光的偏振方向与之平行，此时，只能在垂直于该方向上探测到偶次谐波信号，他们对该方向上的偶次谐波信号进行了充分地测量，如图9（a）所示，每个光谱是在相同的实验条件下四次测量的平均值，图9（a）中的图例为晶体内峰值电场强度的估计值，范围为（0.54～0.83）×108V/cm 或（1.1～2.7）×1013W/cm2。基于固体高次谐波的带内辐射机制，通过贝利曲率做傅里叶变换后得到的系数与偶次谐波信号的关系，他们重构出了SiO2第一条导带的贝利曲率，并和第一性原理计算得到的结果相比较，两者在数值上近乎一致。

图9 单晶SiO2（α-quartz）贝利曲率的重构［50］Fig.9 Retrieval of Berry curvature in single-crystal α-quartz［50］

通过对几何相位或布里渊区内贝里曲率的积分可以得到布洛赫带的拓扑不变量。布洛赫带的几何和拓扑性质丰富了在电磁场驱动下电子运动的物理现象，而高次谐波为探索贝利曲率和贝利相位提供了全新的手段。

2.2.4 退相干和弛豫过程

在基于密度矩阵的理论框架下，载流子的相互作用主要包括与声子的相互作用、与光子的相互作用、载流子之间的相互作用等，这些相互作用引起了相位相干和弛豫，并影响着非平衡动力学过程。对于光激发系统，在求解密度矩阵的过程中，各个态上的分布概率并不是静态的，而是存在弛豫的过程，由此引起求解混合态密度矩阵演化方程的困难。一方面为了更好地反映实验结果，另一方面为了让求解过程比较简便，我们往往会引入两个参量来描述系统的弛豫过程，即布居弛豫时间T1和相位退相干时间T2。在研究半导体体系中弛豫现象的实验中，测量得到的退相时间T2从几十飞秒到数百飞秒不等［84-86］。但是，将理论计算结果与固体中高次谐波实验数据进行比较［13，15-16，21］，结果表明，往往需要选择很短的退相时间T2～1～3 fs，才能去除一些非谐信号对高次谐波谱的影响。诸多理论工作都对退相干过程进行了讨论［22，87-90］。2016年，GARG M 等采用含Hatree-Fock 项的半导体Bloch 方程模拟SiO2高次谐波的信号并与实验的结果相比较［22］，结果表明，有电子-电子相互作用时的带间极化明显小于单电子近似时的极化，说明了电子-电子相互作用在带间相干衰减中的重要作用。DU T 等基于含时薛定谔方程引入声子和电子的相互作用，探讨了声子对退相干时间的影响［89］。有相关的理论研究认为，传播效应也会影响退相干过程［91］。然而，在少周期的强激光脉冲与固体相互作用的过程中，超快的退相时间是否有物理意义，以及如何平衡计算的复杂性和理论描述的完整性，仍然有许多问题亟待解决。

2.3 计算方法

随着固体高次谐波实验的快速进展，许多优秀的理论工作［15，23，35，38-39，52，58-59，62，65，68-69，73-74，76，92-116］接连涌现。基于含时薛定谔方程［23，52，69，71，88-89，96，99-103，117-119］、半 导 体Bloch 方 程［15，22，35，38-39，62，68，73，93，97-98，105-107，110，112，120］、含时密度泛函理论［87，94-95，113，115，121-125］的数值方法被广泛应用于固体高次谐波的模拟研究。理论计算不仅仅在探索固体高次谐波的内在机制上有许多突破，在预测新的实验现象、新奇材料的非线性光学响应［125-127］和更多物理问题如电声子耦合［89，128］、强关联体系［129］、拓扑相变［83，94，130-131］等方面也有广泛的应用。

2.3.1 含时薛定谔方程

含时薛定谔方程（Time-Dependent Schrödinger Equation，TDSE）一直被广泛用于描述激光与物质相互作用的系统。在偶极近似和单电子近似的基础上，采用原子单位制，含时薛定谔方程一般可以写作

式中，(t)是包含激光场含时演化的哈密顿量。早在1992年，PLAJA L 等［52］就通过求解Bloch 基组下的TDSE 计算了Si 的高次谐波信号。许多理论研究者通过求解TDSE 对固体高次谐波的产生机制进行了深入的探讨。

基于Bloch 基组和Houston 基组，WU M 等［69］通过求解速度规范下的TDSE 得到固体高次谐波谱的多平台结构。图10（a）为一维周期性有效势下单电子的能带结构，他们通过计算包含全部51 条能带的高次谐波谱和只包含第4、5 两条能带的高次谐波谱并进行比较，如图10（b）所示，发现初级平台来源于价带和较低的导带，而二级平台来源于更高导带的贡献。随后，他们［23］采用TDSE 方法成功模拟并解释了固体Ar 的高次谐波实验结果。2017年，LIU L 等［132］通过求解TDSE，研究了不同实空间产生的高次谐波的相干现象。2016年，LI L 等［100］采用二维的Kronig-Penney 势，通过求解TDSE 研究了近红外激光场中二维准周期性结构的电离和高次谐波产生过程，发现光电子动量谱明显受二维准周期势的控制。2018年，通过与一维情况比较，JIN J 等［101］发现由于二维能带结构中存在许多交叉点，特别是能量更高的导带可以通过这些交叉点逐步激发，谐波的总贡献是由不同导带簇之间混合跃迁到价带得到的。

近年 来，BIAN X 等还利用TDSE计算了水分子链［117］和准晶的高次谐波谱［118］。WANG G 等［90］在TDSE 的哈密顿量中引入了虚势来描述固体高次谐波产生过程中的退相过程，并与实验和求解半导体布洛赫方程的结果相比较，验证了该非厄米的哈密顿量的有效性。最近，DU T 等［89］利用晶格振动模型探究了电子-声子散射对高次谐波谱的影响，并估算了电子-声子散射的时间尺度。虽然TDSE 计算仅考虑模型体系，但是能非常直观地阐明物理图像。

2.3.2 半导体布洛赫方程和密度矩阵方程

强激光与半导体相互作用的动力学可以用固体能带理论描述。近年来，半导体布洛赫方程（Semiconductor Bloch Equations，SBE）模型已被成功地用于研究固体中谐波发射和电流的性质。本节中介绍SBE 方法及其在固体高次谐波研究中的改进。基于Bloch 基组的长度规范和Houston 基组的速度规范下的半导体布洛赫方程分别如（13）和（14）式所示。

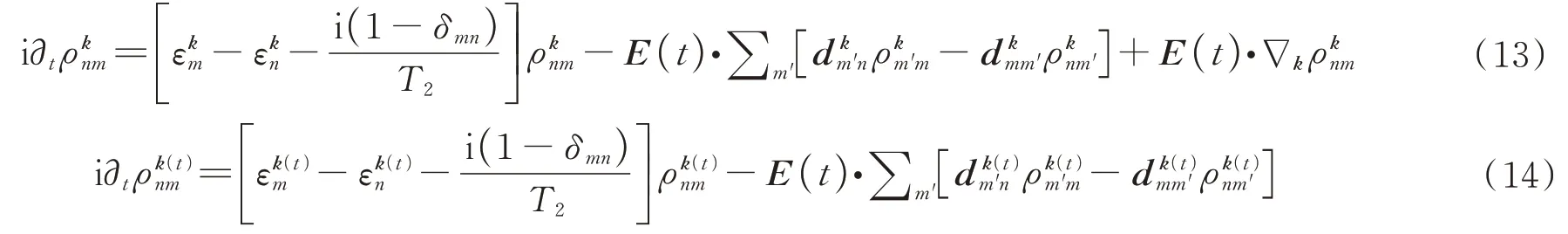
基于两能带SBE，GOLDE D 等［68，133］研究了在超短强激光脉冲和太赫兹场激发下半导体纳米结构的发射辐射。他们发现带内加速显著地改变了带间极化的动力学，导致了高阶极化的强烈增强。密度矩阵方程（Density Matrix Equations，DME）和半导体布洛赫方程系出同源。VAMPA G 等［73］利用两能带模型的DME 分析了ZnO 体系的带间极化和带内电流，其中带间机制和带内机制占主导的高次谐波频谱范围不同，平台区的谐波产生主要来自于带间机制，最小带隙以下的谐波来源于带内机制。此外VAMPA G 还发现了带内和带间机制下的高次谐波表现出不同的波长依赖，中红外波长驱动下带间机制占主导作用，远红外驱动下主要是带内机制贡献了高次谐波。VAMPA G 等通过［35］双色激光场驱动产生高次谐波，证明了利用高次谐波重构固体能带结构的可行性。在接下来的理论工作中，SBE 也从两能带模型拓展到多能带模型，并在实验和理论上证实，每对能带之间不同激发路径的量子干涉是重要的，因此可产生偶次谐波辐射［15，92，98］。

伴随着量子力学和原子分子光谱学的发展，电子态（能级）之间的跃迁过程可以在几率波的理论框架下用跃迁偶极矩来描述，跃迁偶极矩对应着量子态之间的激发或者辐射过程。SBE 中的跃迁偶极矩及其相位的重要性也被多次探讨。YU C 等［105］改进了SBE 模型，并利用第一性原理计算出SiO2的真实偶极矩进行了模拟，发现价带和导带间的偶极矩幅值和形状在谐波发射中起着重要作用。由于量子力学中的波函数是复数，需仔细考虑跃迁偶极矩的相位与幅值才能合理解释跃迁相关的光学性质及动力学。2017年，JIANG S 等［106］发展了引入跃迁偶极矩相位的SBE 模型，并针对石墨烯的跃迁偶极矩相位进行讨论，指出偶次谐波信号的产生和跃迁偶极矩相位、晶体对称性之间联系紧密。2018年，JIANG S 等［108］通过对ZnO 晶体取向依赖的高次谐波模拟，与实验进行对比，发现跃迁偶极矩相位是反映物质结构及电子结构对称性的关键物理量，阐明了跃迁偶极矩相位对偶次谐波产生的重要意义。近年来，理论研究者针对半导体布洛赫方程的规范不变性进行了讨论［107，134-135］。由于SBE 的计算需要本征能带、跃迁矩阵元等信息作为输入信息，第一性原理计算往往会产生随k变化的随机相位因子exp(i)，我们称此规范为任意规范，不同的规范选择也导致了不同的跃迁偶极矩阵元。然而规范不变性告诉我们，不论选择何种Bloch 波函数的相位进行数值计算，我们都应该获得相同的结果。SBE 可通过TDSE 严格推导得到，是规范不变的，而由于早期的SBE 在计算跃迁矩阵元时忽略了贝利联络，导致计算结果受到规范变化的影响［134-135］。因此，贝利联络和易于进行数值计算的规范被提出，并应用于SBE 模拟。

在前人工作的基础上，2022年QIAN C 等［83］基于Houston 基组下的SBE 模型，在鞍点方程中发现位移矢量将贝利联络（和分别为导带和价带的贝利联络）和跃迁偶极矩相位（ϕkcv）结合在一起构成一个具有完善物理意义的规范不变量。如图11 所示，在波形虚线中用蓝色和红色点分别标记实空间中导带和价带的电荷中心，在非中心反演对称的体系中，不同能带的电荷中心存在偏移。除了能量的变化外，电子-空穴在实空间中的位置也随着激光场E（t）的振荡而变化。在空间反演对称破缺的晶体材料中，当电子经历非绝热跃迁时，可用位移矢量来描述光激发电子和空穴的实空间位移。他们首次揭示了强激光场下位移矢量在电子隧穿过程中的重要作用。由于位移矢量的存在，激光场中电子隧穿时遇到的势垒将发生变化，辐射光子的能量将受到外加光场和位移矢量的联合调制。因此，激光场的反向导致不一致的物理过程，谐波每半个光学周期产生一次相同辐射的规律被打破，这是非中心对称体系下偶次谐波产生的重要物理机制。此外，位移矢量还包含相关波函数的拓扑性质，考虑位移矢量的高次谐波辐射能够直接反映非中心对称拓扑绝缘体相变时的能带反转现象。在Kane-Mele 模型和真实材料BiTeI 中，均发现在拓扑相变过程中，当发生能带反转时，位移矢量亦会反向。在振荡强激光驱动下，位移矢量的反向导致时域上完全相反的高次谐波辐射。利用该时域上的谐波特性，有望实现对非中心对称拓扑绝缘体的能带反转性质的全光探测，为探测非中心反演对称材料的拓扑相变提供了新途径。

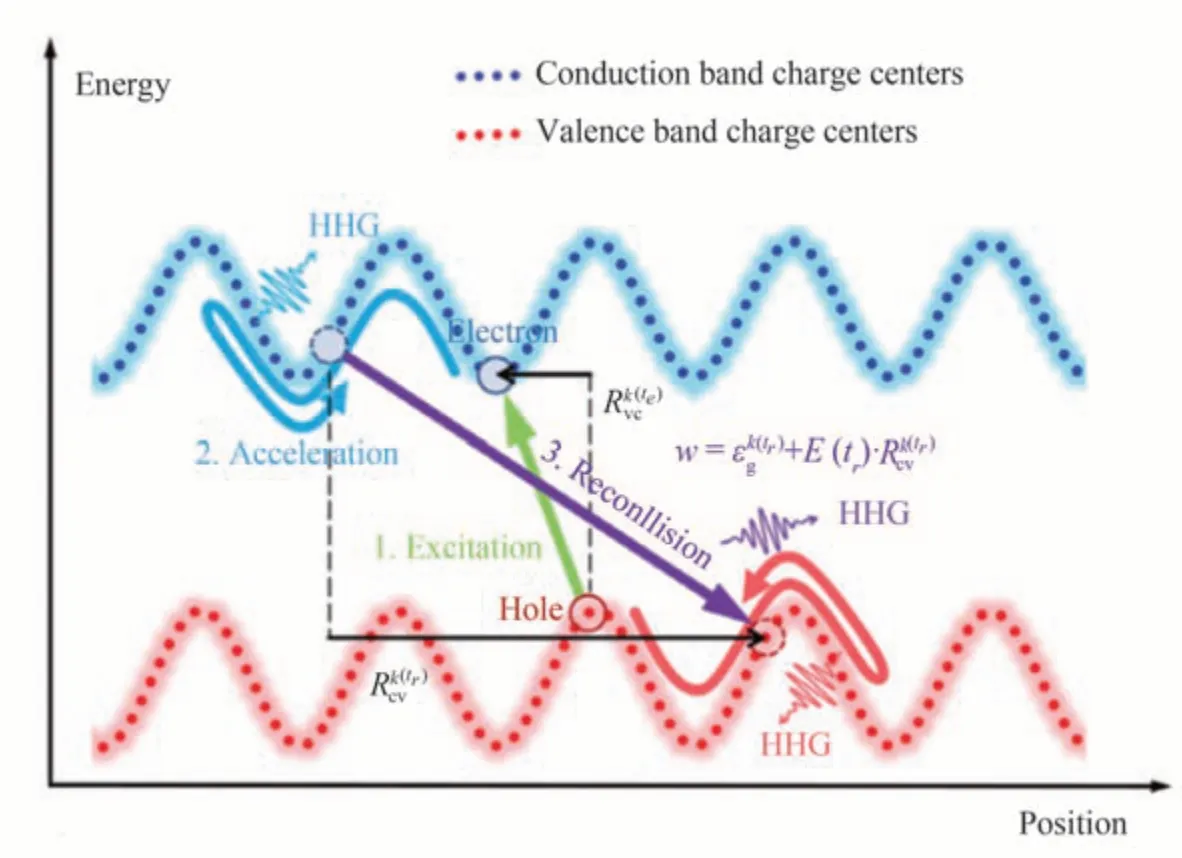
图11 非中心对称系统高次谐波辐射的实空间表示［83］Fig.11 Real-space representation for HHG from noncentro symmetric systems［83］

SBE 和DME 是模拟固体高次谐波的重要理论工具，可以直观描述真实材料的高次谐波产生过程。该理论框架有待进一步完善，例如：如何引入激子、声子等准粒子与载流子的相互作用等。

2.3.3 含时密度泛函理论

含时密度泛函理论（Time-Dependent Density Function Theory，TDDFT）是一种基于求解含时Kohn-Sham 方程，在实空间实时模拟材料电子结构的第一性原理计算方法。通过求解含时Kohn-Sham 方程的数值积分可以获得体系的电子密度，模拟分子和凝聚态体系的非绝热演化过程，并且能够在微扰和非微扰范围内得到电子波函数在时域上的演化动力学。已有许多理论研究者采用TDDFT 计算方法，研究了激光诱导固体高次谐波［［94-95，113，115，136］和电流［114，137］的微观起源。

TANCOGNE-DEJEAN N利用［138］TDDFT结合自洽Hubbard U方法，证明动态调制U值在描述NiO高次谐波产生中的重要性。FLOSS Ⅰ等［136］则结合TDDFT 模型和多能带SBE 模型，对固体高次谐波进行了从头算多尺度模拟，发现传播效应和场的非均匀性对谐波谱的影响，他们还在后续的工作中引入退相干效应［87］。近年来，QIN R 和CHEN Z 等利用TDDFT 计算了硅烯［126］、黑磷［125］、石墨烯/hBN 异质结［122］等体系的高次谐波，利用高次谐波信号结合TDDFT 探测晶体结构的手性［139］、硅的结构相变［123］等。2018年，BAUER D 等［94］利用TDDFT 研究了有限长一维周期性模型的两种拓扑相，发现拓扑边缘态引起高次谐波谱明显的相干增强效应，该工作首次将强场物理与拓扑凝聚态物理相结合。

2018年，TANCOGNE-DEJEAN N 等［140］以单层h-BN 为例，采用TDDFT 计算，理论上提出了二维材料的类原子（atomic-like）谐波。基于材料电子的“电离-加速-复合”三步过程，类似于原子体系的高次谐波机制，斜入射的飞秒强激光驱动材料的价带电子电离到表面外的真空区域，随电场加速运动，当激光电场反向后，电子与母体材料复合，释放高能光子，该固体谐波方案的截止能量约80 eV 并满足Ecutoff=Ew+3.17Up（Ew为材料的功函数），如图12（a）、（c）所示。在类原子谐波基础上，2020年YU C 等［127］发现双层、多层纳米结构中的电子背散射可大大拓展高次谐波的截止能量，如图12（b）、（d）所示。他们在TDDFT 的数值实验基础上发展了半经典理论模型，提出了基于材料电子“电离-背散射-加速-复合”的新机制。该新机制的谐波截止能量（＞200 eV）突破了Ew+3.17Up的限制，且不依赖于堆垛方式和材料种类，并可利用更多层的纳米结构阵列进一步提高谐波效率，相比分子体系更优越、更易实现且具有普适性，为极紫外、软X 射线等先进光源提供了新的理论方案。尽管TDDFT 对计算资源要求很高，该方法将成为模拟高次谐波和强场超快物理过程最有效的工具之一。

图12 单层h-BN 的三步模型［140］、双层h-BN 的四步模型及相应的高次谐波谱［127］Fig.12 Three-step model for monolayerh-BN［140］and four-step model for distant bilayer h-BN，and corresponding high-order harmonics spectra［127］

3 总结与展望

由于固体中原子排列密集，在相同驱动激光条件下固体高次谐波的产生效率相比气体介质高很多。然而，固体靶材因损伤阈值的影响，所使用激光的输入功率将严重受限，因此寻找高损伤阈值的固体靶材或者通过改性提高材料的损伤阈值是获得更高能量的固体高次谐波的可行方案。同时，固体高次谐波对于晶体的厚度很敏感，谐波穿过晶体时容易相位失配以及可能被吸收，未来需进一步考虑传播效应、材料本身的光学吸收性质对高次谐波辐射的影响。

固体高次谐波研究作为一个凝聚态物理与强场激光物理交叉的研究方向，正在快速发展并取得新的突破。通过对固体高次谐波空间分布和时间分布的精密测量，能以高时空分辨率反映晶体的结构信息［21，35，50］。虽然目前利用高次谐波重构晶体的能带结构［21，35］、贝利曲率［50］等方法仅适用于最低的导带和最高的价带，但是高次谐波信号中仍然有许多信息等待我们去发掘，这为研究者们探索物质的性质提供了非常有潜力的光学方案。固体高次谐波谱也为探索固体中各种准粒子的相互作用提供了有效的手段，在MoS2实验［25］中单层材料相比于块体材料更高的谐波效率以及固态稀有气体实验中第二平台出现时对应的能量［23］，都体现了准粒子之间的相互作用以及多体效应与高次谐波信号之间的关系。尽管理论上还有许多困难需要克服，但高次谐波光谱将成为物质内部相互作用和相关非平衡态动力学研究的一种重要技术。

除此以外，固态高次谐波在新型紧凑光源方面拥有良好前景。各种纳米结构［19，28-29］的高次谐波实验表明，结合电子工程和纳米工程技术，从人工超材料或超结构角度出发，有望实现对高次谐波空间和相位上的调控，为获取强度更高、单光子能量更高的新型光源提供新的思路。

高次谐波的研究，从原子的“三步模型”［7］到晶体的“三步模型”［11，58-59］，如今推广到晶体的类原子谐波及层状纳米结构的“四步模型”［127，140］，乃至具有转动周期性结构的类固体谐波［141］等等。固体高次谐波的研究范围正在逐渐扩大，并与其他领域结合、发展，将展现长久的生命力和巨大的应用潜力。