反比例函数中图形面积问题的解题技巧

◎赵振海

(山东省东营市垦利区第二实验中学,山东 东营 257500)

中考题通过改变与本知识点关联的图形来体现新颖的出题特点，从而实现试题对不同难度和能力水平的考查2020年中考题，题目类型十分丰富，解题方法更是多种多样

一、直接应用数形结合实现面积值与k值的互求

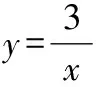
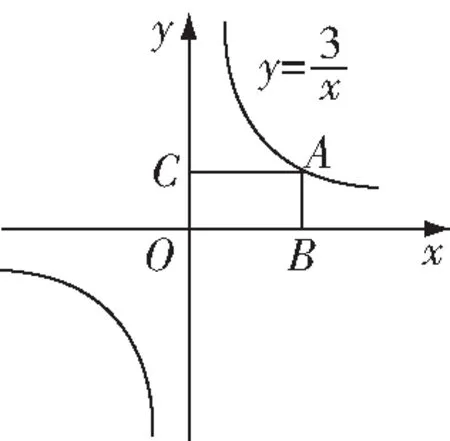
图1

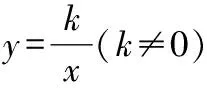
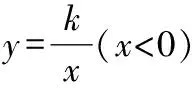
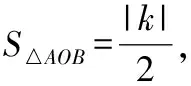
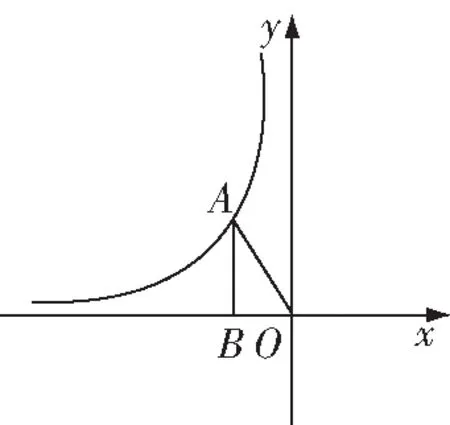
图2

∵⊥，

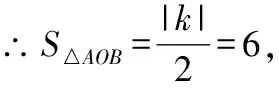
∴=±12，

∵反比例函数的图像在二四象限，

∴<0，

∴=-12

故答案为-12

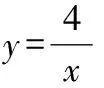
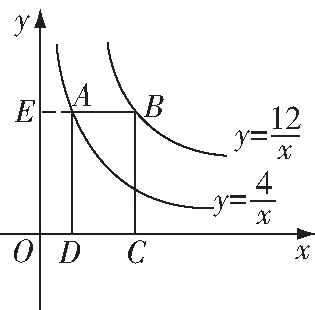
图3

A.4 B.6 C.8 D.12

解：过点作⊥轴，垂足为，

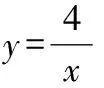
∴四边形的面积为4，

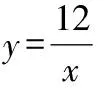
∴四边形的面积为12，

∴矩形的面积为12-4=8

故选C

二、运用简单不规则图形面积的和差转换巧求面积

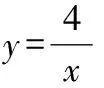
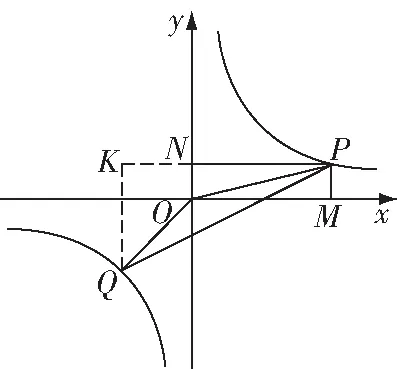
图4

A.∶=2∶3 B.∶=1∶1

C.∶=4∶3 D.∶=5∶3

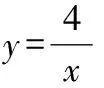
∴×1=-2=4，

∴=4，=-2

∵(4，1)，(-2，-2)，过点分别向轴,轴作垂线，垂足分别为点，，

∴=4作⊥，交的延长线于，则=4，=1，=6，=3，

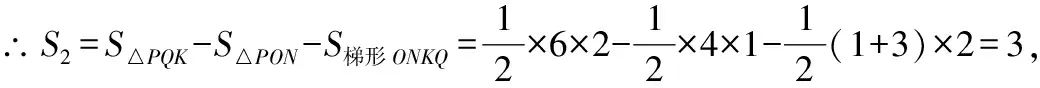
∴∶=4∶3

故选C

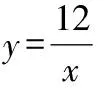
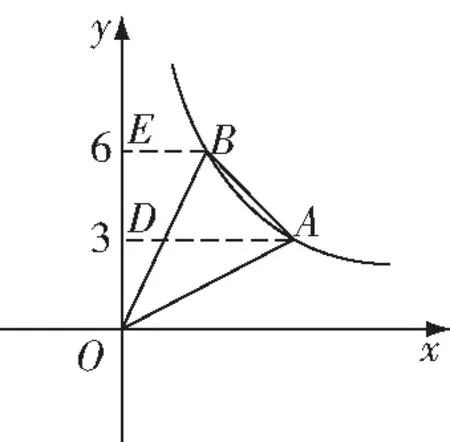
图5

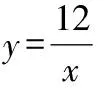
∴(4，3)，(2，6)作⊥轴于，⊥轴于，

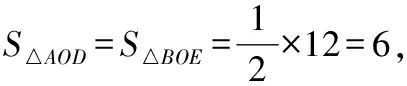
∵△=△+梯形-△=梯形，

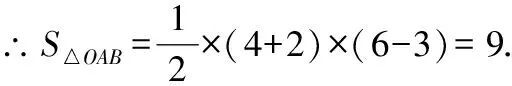
故答案为9

以上两个题目都出现了不规则的斜三角形，它们没有在坐标轴上的一条边，因此我们不能一眼看出其面积和值的关系，它们的求解均是通过割补法进行的，都是将斜三角形变成矩形、直角三角形、直角梯形的代数和，如第4题，=△-△-梯形解此类题目的关键就是向坐标轴作垂线割补原图

三、巧用组合图形面积值和方程思想逆向求得k值

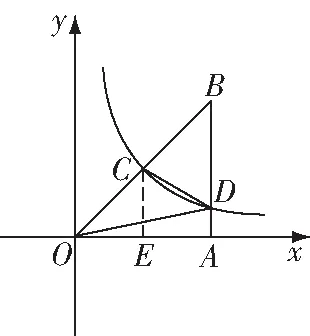
图6

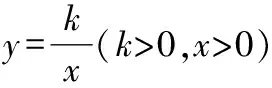
解：根据题意设(，)，则(，0)，

∵点为斜边的中点，

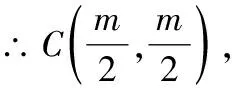
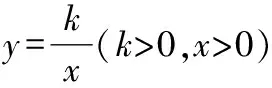
∵∠=90°，

∴的横坐标为，

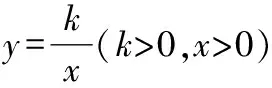
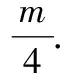
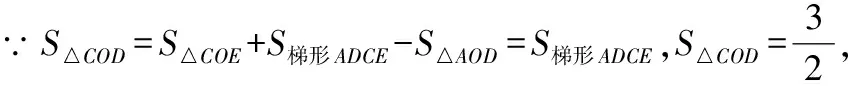
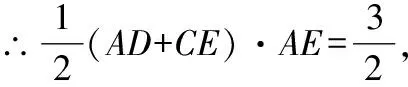
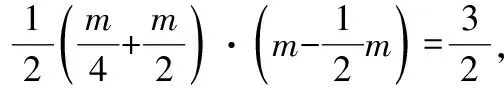
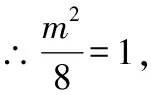
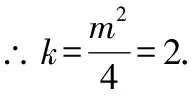
故选C

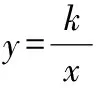
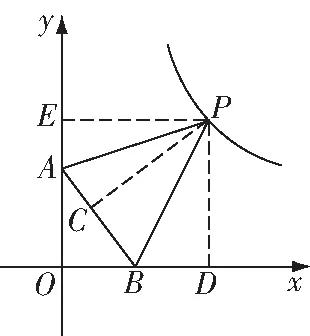
图7

A.36 B.48 C.49 D.64

解：过分别作,轴,轴的垂线，垂足分别为,,，如图7，

∵(0，4)，(3，0)，

∴=4，=3，

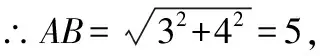
∵△的两个锐角对应的外角平分线相交于点，

∴=，=，

∴==，设(，)，则=

∵△+△+△+△=矩形，

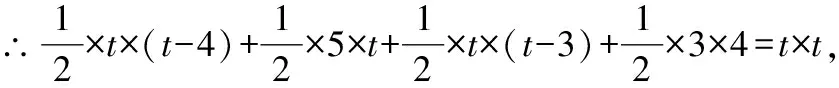
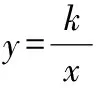
故选A

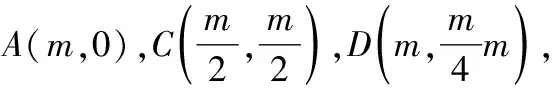
四、巧用三角形全等或等积规律求图形面积或反求k值

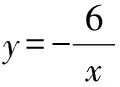
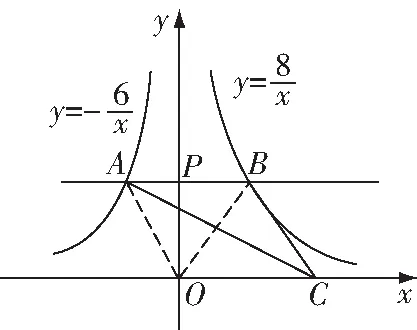
图8

A.6 B.7 C.8 D.14

解：∵∥轴，且△与△共底边，

∴△的面积等于△的面积，连接，，如图8所示

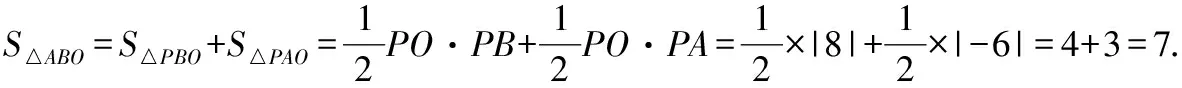
故选B

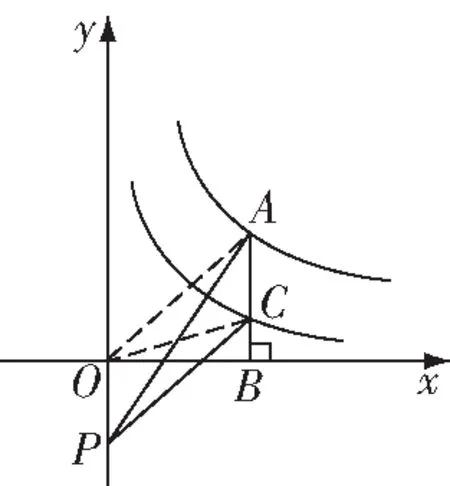
图9

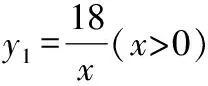
A.5 B.6 C.11 D.12

解：连接和，

∵点在轴上，则△和△面积相等，

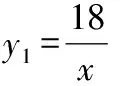
∴△=△-△=6，

∴△的面积为6

故选B

以上两题中均有一个“跑偏”的三角形，解决方法都是运用等积变换将“跑偏”的三角形替换成目标三角形如第9题连接和，利用等积法可得△的面积即△的面积，再结合反比例函数中系数的意义，利用△=△-△，问题迎刃而解

五、运用相似巧求目标三角形面积值反求k值

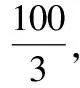
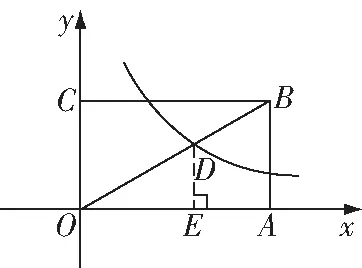
图10

解：∵为矩形,

∴⊥轴，作⊥轴，

∴∥,

∴△∽△,

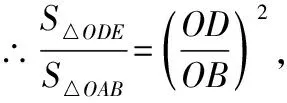
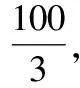
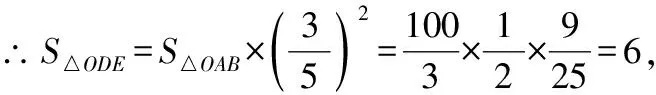
∴=6×2=12

故答案为12

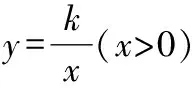
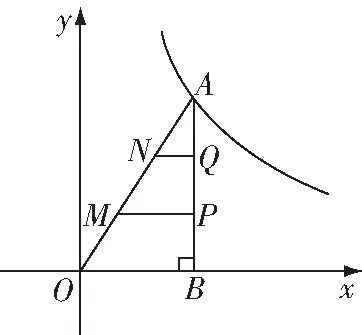
图11

A.9 B.12 C.15 D.18

解：∵∥∥，

∴△∽△∽△，

∵，是的三等分点，

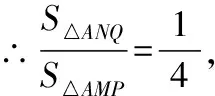
∵四边形的面积为3，

∴△=1

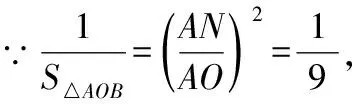
∴△=9，

∴=2△=18

故选D.

以上两题均运用相似三角形的性质——面积比等于相似比的平方，求得目标三角形面积，进而可求出的值