并联式踝关节康复机器人的运动学分析及其优化*

芦风林,张彦斌,王科明,魏雪敏,常振振

(河南科技大学 机电工程学院,河南 洛阳 471003)

0 引 言

人体能够完成正常活动与踝关节的作用密切相关,其状态的好坏直接决定着人的生活质量的高低。由于踝关节是人体距地面最近的关节,几乎承担着人体的全部重量,再加上随着人口老龄化的加剧和交通事故的增多,踝关节损伤现象变得愈发常见[1，2]。

为了加快患者的康复,除了进行早期药物治疗和手术治疗外,还有必要进行科学的康复训练[3，4]。传统的康复训练多是由康复理疗师辅助患者进行一对一的训练,其成本较高,康复效果也受到其自身经验、水平等因素的影响[5]。

为解决现阶段传统康复手段的不足之处,国内外已有诸多学者尝试了将机器人技术应用于人体踝关节的康复训练[6-8]。

ZHANG M M等人[9-10]提出了一种具有3个旋转自由度的踝关节康复机器人(CARR),其运动平台和基座由4个可伸缩的SPS链连接,通过4个柔性执行器的同时运动来实现其康复训练功能。ERDOGAN A等人[11]提出了一种用于踝关节康复的可重构外骨骼机构,以3-RPU和3-UPU为基础结构,可重新配置,有助于反复改变和重新安排机器人外骨骼的部件。RUSSO M等人[12]基于S-4SPS并联机构,设计出了一种用于踝关节康复训练的轻型可穿戴装置,并通过数值模拟验证了其可行性。李剑锋等人[13-14]研制出了一种三自由度转动2-UPS/RRR型踝关节康复机构,可保证人-机转动中心近似重合,并对机构的运动学和工作空间进行了分析。曾达幸等人[15]提出了一种具有解耦特性的并联式踝关节康复机构,其能够实现跖屈和背伸、内收和外展运动的单独转动康复,以及在牵引下转动的康复过程。陈子明等人[16]基于3-UPU并联机构,设计出了一种踝关节康复机构,其转动轴线可实现高度和角度方向的调节。

上述文献中提到的踝关节康复机器人机构都具有其自身的优点,但同时存在不足。如:有的机构转动中心与踝关节运动中心存在偏移,有的机构转动中心位置固定,有的存在穿戴不便的问题。

基于2-RURU/RR型并联机构,笔者设计一种新型踝关节康复机器人,利用螺旋理论对机构自由度进行分析和计算,建立其运动学求解模型,利用数值搜索法求得机构的工作空间,基于运动/力传递性能指标研究机构运动性能和参数优化设计,并进行运动学仿真分析和物理样机搭建。

1 踝关节康复机器人的设计

1.1 人体踝关节的生理运动分析

人体踝关节连接着足部与小腿,由颈骨、腓骨下端的关节面和距骨滑车连接而成,是人体重要的负重及运动关节,其周围韧带和肌肉保障了踝关节在运动过程中的高度稳定性。

踝关节的运动较为复杂,分析时可将脚踝的运动描述为近似于球铰沿3个方向的转动,如图1所示。

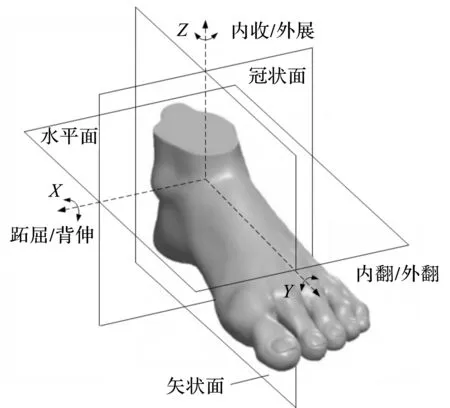
图1 人体踝关节的运动形式

由图1可知：根据矢状面、冠状面和水平面,可将踝关节分为左右部分、前后部分和上下部分的切面;3个方向的转动分别为矢状面中绕X轴的跖屈和背伸,冠状面中绕Y轴的外翻和内翻,水平面中绕Z轴的外展和内收。

从踝关节骨性结构方面考虑,踝关节的主要运动方式为跖屈/背伸和内翻/外翻运动,而外展/内收的运动主要由小腿来实现。

踝关节是重要的下肢稳定关节,康复训练应以恢复其稳定性为主。根据踝关节的生理功能及临床数据可知:在踝关节康复过程中,主要考虑的是背伸/跖屈和内翻/外翻的训练[17]。

研究数据表明,由于性别和年龄上的不同,个体之间的踝关节活动度存在显著差异。其中,踝关节在矢状面内的活动度在65°～75°之间,冠状面的总活动度约为35°。

但在日常步态活动中,矢状面所需的活动度大大减少,最大约为30°。踝关节具体的活动度范围如表1所示[18]。

表1 踝关节的活动度

1.2 并联式踝关节康复机器人结构设计

基于2-RURU/RR型并联机构,笔者设计出一种新型踝关节康复机器人的简化模型,如图2所示。

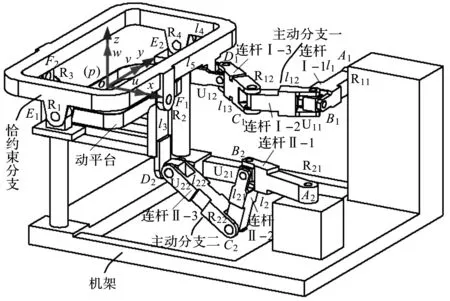
图2 踝关节康复机器人的简化模型

由图2可知:踝关节康复机器人机构主要由机架、动平台(脚踏板)、2条主动分支和2条恰约束分支组成。2条主动分支结构相同,分别由2个转动副(R)和2个万向铰(U)组成,运动副的布置顺序依次为RURU;2条恰约束分支均由2个轴线垂直的转动副构成,即为RR型分支。由于第一条恰约束分支两转动副R1、R2分别与第二条约束分支两转动副R4、R3共轴线,因此第二条约束分支可视作虚约束分支,但其存在可增强机构的刚度和承载能力。

同时,两约束分支中的4个转动副轴线共面,并均安装于矩形构件上。机构动平台(脚踏板)通过转动副R2(R3)与矩形构件相连。第一条主动分支R11U11R12U12中转动副R11直接与机架相连,万向铰U12安装于矩形构件上且其末端转动轴线与R1轴线平行。

根据图2还可知:第一条主动分支与恰约束分支构成了一条混合运动链;第二条主动分支R21U21R22U22中转动副R21直接安装在机架上,万向铰U22直接与动平台相连,且其末端轴线平行于R2轴线。笔者建立定坐标系o-xyz,其原点o位于2条恰约束分支中转动副轴线的交汇处,y轴与转动副R1轴线重合,z轴竖直向上,x轴可由右手准则确定。第一条主动分支中转动副R11轴线平行于x轴,第二条主动分支中转动副R21轴线平行于z轴。笔者选取与机架直接相连的运动副R11和R21作为机构的主动副。

笔者所提的2-RURU/RR型踝关节康复机器人的转动中心可调节,并且具有恰约束分支,相较于前述文献中的踝关节康复设备,其具有承载能力强、安全性高和适用范围广等优点,且机构具有无耦合运动特性,可实现1条主动分支控制动平台1个方向的转动自由度。

2 康复机器人机构的运动学分析

2.1 自由度分析

笔者建立动坐标系p-uvw(图2),其中,坐标原点p与o点重合,u轴与R2轴线重合,v轴与R1轴线重合,w轴可由右手准则确定。假定在初始位置时动坐标系与定坐标系的对应轴线重合。α和β分别为动平台绕x轴和y轴的旋转角度;q1和q2分别为2条主动分支的输入角位移。

在定坐标系o-xyz下,机构第一条主动分支的运动螺旋系可表示为:

$11=(1 0 0;0b11c11)
$12=(1 0 0;0b12c12)
$13=(0 0 1;a13b130)
$14=(0 0 1;a14b140)
$15=(0 0 1;a15b150)
$16=(0 1 0;-l4sβ0l4cβ)

(1)

式中:a1m，b1m，c1m(m=1,2,3,4,5,6)—对应运动螺旋位置相关的参数;l4—万向铰U12的中心到转动副R1轴线距离;s(·)—角度正弦;c(·)—角度余弦。

式(1)表明:第一条主动分支运动螺旋系为六系螺旋,故该分支对机构不提供任何约束。

由图2可知:第一条主动分支与第一条恰约束分支中转动副R1形成一个空间闭回路,所以在进行自由度分析时,可将这2条分支构成的混合运动链等效为第一条恰约束分支,则等效分支的运动螺旋系为:

(2)

根据互易积原理,可求出该等效分支的约束螺旋系,即:

(3)

同理,第二条主动分支的运动螺旋系为:

$21=(0 0 1;a21b210)
$22=(0 0 1;a22b220)
$23=(0 1 0;a230c23)
$24=(0 1 0;a240c24)
$25=(0 1 0;a250c25)
$26=(cα0 sα;a26b26c26)

(4)

式中:a2m,b2m,c2m—与对应运动螺旋位置相关的参数;l3—万向节U22的中心到转动副R2轴线距离,且有a26=l3sαsβ,b26=-l3cα,c26=l3sαcβ。

根据式(4)可知:第2条主动分支的运动螺旋系也为六系,因此机构动平台仅受到混合运动链的约束。

根据式(3)知：机构动平台受到3个约束力和1个约束力偶的作用,分别限制了动平台在空间中的3个移动自由度和绕z轴的转动自由度,使得动平台只具有绕x轴和y轴方向的转动自由度。

同时,分析结果表明,该机构不存在冗余约束,故其为非过约束并联机构。

利用修正G-K公式,可计算出机构自由度,即:

(5)

式中:M—机构的自由度;λ—机构的阶数;n—包括机架的构件数目;g—运动副的总数;fk—第k个运动副的自由度数;v—冗余约束数;ζ—局部自由度数。

对于图2所示机构,λ=6、n=11、g=12、∑fk=14、v=ζ=0,将各参数代入式(5),经计算可得M=6(11-12-1)+14=2。

该计算结果与前述理论分析一致,所以可知该机构为二自由度纯转动并联机构。

2.2 机构姿态角位移分析

由图2可知,动坐标系可视为将定坐标系先绕x轴转动α,再绕y轴转动β而得到,则相对于定坐标系的姿态变换矩阵,动坐标系可写为:

(6)

式中:Rx(α),Ry(β)—绕x轴和y轴的姿态变换矩阵。

根据第二条主动分支中,万向铰U22中心点D2在定坐标系o-xyz中的位置坐标,可得:

XD2=RXbD2+X0D2

(7)

式中:XbD2—点D2在动坐标系中的位置坐标,且有XbD2=[l40 -l3]T;X0D2—动坐标系原点在静坐标系中的位置矢量,因机构动、定坐标系的坐标原点重合,故其为零矢量。

通过式(7)可求得点D2位置坐标,即:

XD2=[l4cβ-l3sβcαl3sα-l4sβ-l3cαcβ]T

(8)

根据第二条主动分支运动链与坐标原点o形成的封闭回路(见图2),可建立矢量方程为:

OD2=OA2+A2B2+B2C2+C2D2

(9)

将式(9)向y轴方向进行投影,可得:

l3sα=l2[s(q0+q2)-sq0]

(10)

式中:l2—连杆A2B2的长度;q0—初始位置时连杆A2B2与o-xz平面之间的夹角;q2—主动副R21的输入角位移。

由式(10)可解出动平台姿态角α的值,即:

α=arcsin[l2(s(q0+q2)-sq0)/l3]

(11)

同理,假定机构在初始位置时,连杆A1B1在o-xy平面内,根据D1点的位置坐标可建立第一条主动分支封闭回路矢量方程,并向z轴方向投影,可得:

l4sβ=l1sq1

(12)

式中:l1—连杆A1B1的长度;q1—主动副R11的输入角位移。

因此,可求得姿态角β的值为:

β=arcsin(l1sq1/l4)

(13)

式(11,13)为机构的姿态正解方程,对其进行变形,可得到机构的运动逆解方程,即:

(14)

2.3 角速度分析

将式(10,12)对时间进行一阶求导,并整理成矩阵形式,可得:

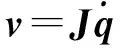
(15)

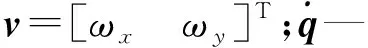
速度雅可比矩阵J为:

(16)

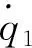
3 康复机器人姿态空间分析

工作空间是衡量机构工作性能的一项重要指标,也是机构设计分析中的重要一环。由于并联机构分支较多,约束影响因素也较多,导致工作空间求解难度增大。影响图2中踝关节康复机器人姿态空间的主要因素有3种:

(1)主动副转角范围

笔者考虑机构的实际结构和装配条件的限制,主动副的约束条件设定为:

qimin≤qi≤qimax

(17)

式中:qimin，qimax—第i条分支主动副的最小和最大极限转角,且有qimin=60°,qimax=50°。

(2)非主动运动副转角范围

万向铰与转动副的转角范围均与运动副具体结构形式有关,为保证机构正常工作,需满足:

|θj1|≤θjmax|δ1|≤δ1max|δ2j|≤δ2jmax

(18)

式中:θj1—转动副Rj2的转角(j=1,2),其转角范围的最大值均为θ1max=θ2max=75°;δ1—万向铰U11、U12和U13的转角,其2个转轴的转角范围相同,且有δ1max=45°;δ2j—万向节U21的转角,其2个转轴的转角不同,令δ21max=60°,θ22max=90°。

(3)分支运动奇异位形

为避免机构在工作空间中发生奇异,需对动平台的位姿加以限制。对于踝关节康复机器人而言,其动平台转动范围应满足-45°≤α≤25°,-25°≤β≤25°。为使其能够实现两脚同时康复训练,避免机构产生奇异,需要取动平台的可达姿态空间为实际所需工作空间的1.2倍,故笔者将机构的空间姿态参数设为:

-54°≤α≤30°
-30°≤β≤30°

(19)

参照国标GB 10000—1988《中国成年人人体尺寸》规划动平台尺寸,即点D1距轴线E1E2的距离l4=150 mm,点D2距轴线F1F2的距离l3=130 mm,笔者设定机构的初始结构尺寸参数,如表2所示。

表2 机构的初始结构尺寸参数

表2中:结构尺寸l11=B1C1,l12=C1D1,l21=B2C2,l22=C2D2。

根据给定的结构尺寸参数和约束条件,可通过MATLAB软件搜索出机构可达点的集合。笔者设定搜索步长为Δα=Δβ=1°,计算出该踝关节康复机器人动平台的姿态空间[19],如图3所示。

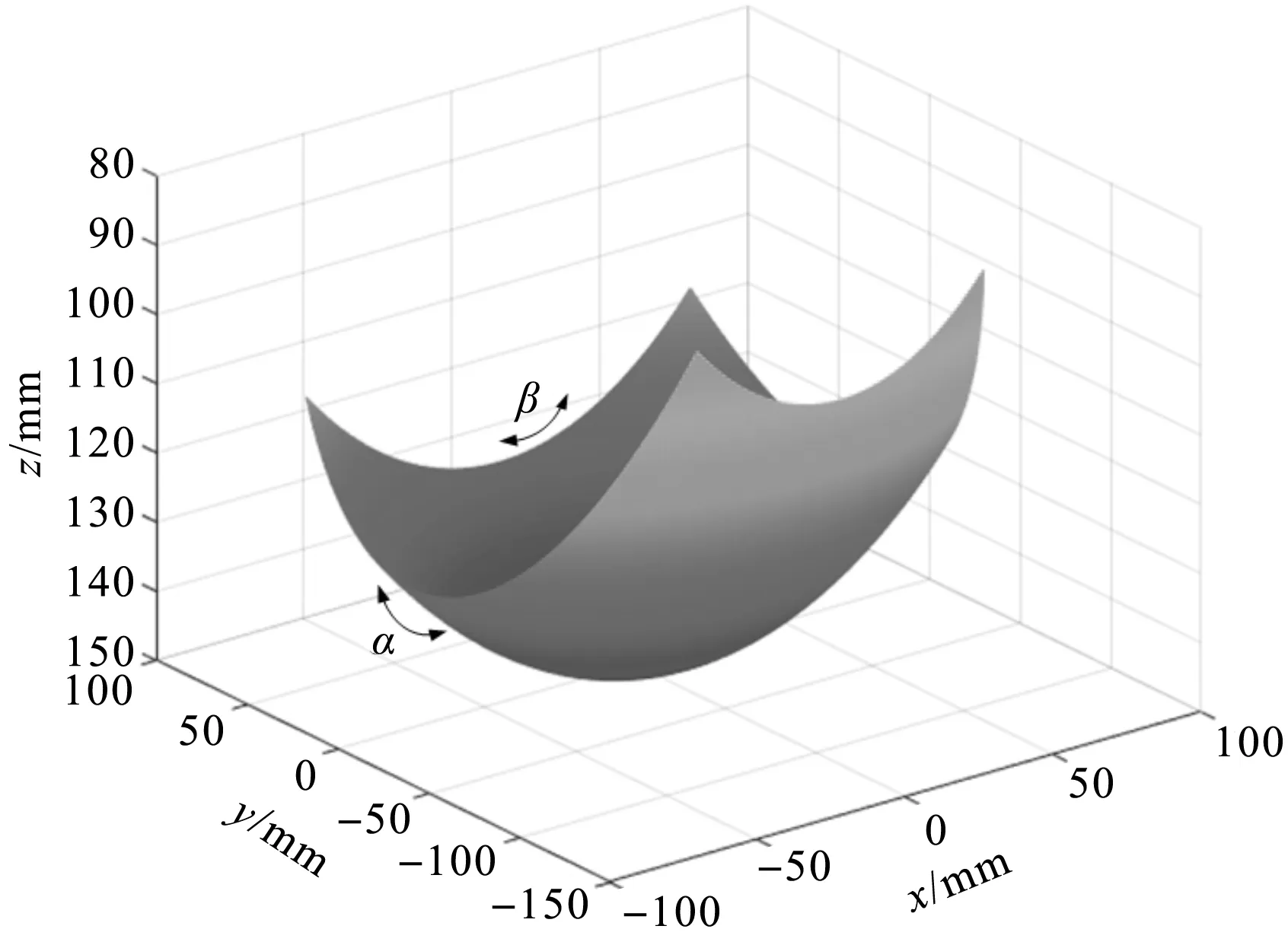
图3 康复机器人动平台姿态空间

由图3可知:康复机器人动平台姿态空间中没有出现突变及空洞的现象,并可以相应地计算出机构动平台的最大转角范围为α∈[-91.58°,70.06°],β∈[-72.24°,72.13°]。

4 运动/力传递性能分析及尺度优化

性能分析是并联机构能否应用于实际工作的直接判定条件,也是机构进行尺度优化的重要依据。运动/力传递性能直接反映了机构从输入端到输出端的传递效率,且无量纲,其数值大小可方便进行比较。

笔者将利用分支局部传递指标(LTI)和全域优质工作空间性能指标(GTW)[20，21]分析机构的运动性能。

4.1 局部传递性能指标

在并联机构中,各分支的传递力螺旋分别与其对应分支的输入运动螺旋和输出运动螺旋之间的传递效率,被称为该分支的输入传递性能指标和输出传递性能指标,即:

(20)

(21)

式中:$Ii—分支i的输入运动螺旋;$oi—分支i的输出运动螺旋;$Ti—分支i的传递力螺旋;λi—分支i的输入传递性能指标;ηi—分支i的输出传递性能指标。

由式(20,21)可知:当输入传递指标λi和输出传递指标ηi取值越接近于1时,则分支的运动/力传递性能越好;当其值较小或趋于0时,则表示该分支的运动/力传递性能较差,即机构位于奇异位形处或临近点。

并联机构分支运动链的数目不少于2条,当动平台处于不同位置时,各分支输入与输出传递性能也随之产生变化。因此,笔者需考虑并联机构所有分支的运动/力传递性能,并取其中的最小传递效率作为该机构的局部传递性指标(LTI),即:

γ=min{λi,ηi}

(22)

式中:γ值与坐标系的选取无关。

以第1条主动分支为例,其运动螺旋系为式(1),根据传递力螺旋$T1与该分支中非主动运动螺旋互易积为零的特性,得:

$T1°$1i=0(i=2,3,4,5,6)

(23)

根据式(1,23)求得:

$T1=[0 0 1;l5-l4cβ0]

(24)

式中:l5—万向节U12的中心到o-xy平面的距离。

同理,可求得第2条分支的传递力螺旋$T2为:

$T2=[0 1 0;k0 -l2c(q0+q2)]

(25)

其中,k=(l2c(q0+q2)sβ+l3cα)/cβ。

由于机构具有无耦合运动学特性,即当锁定一条主动分支的主动副后,动平台将仅有一个转动自由度,且其转动轴线分别为约束分支的两个转动轴,则机构的输出运动螺旋可分别表示为:

$O1=[0 1 0; 0 0 0]
$O2=[cβ0 sβ;0 0 0]

(26)

将式(24～26)代入式(20～23)中,可计算出机构在姿态空间的运动/力传递性能,其分布图谱如图4所示。

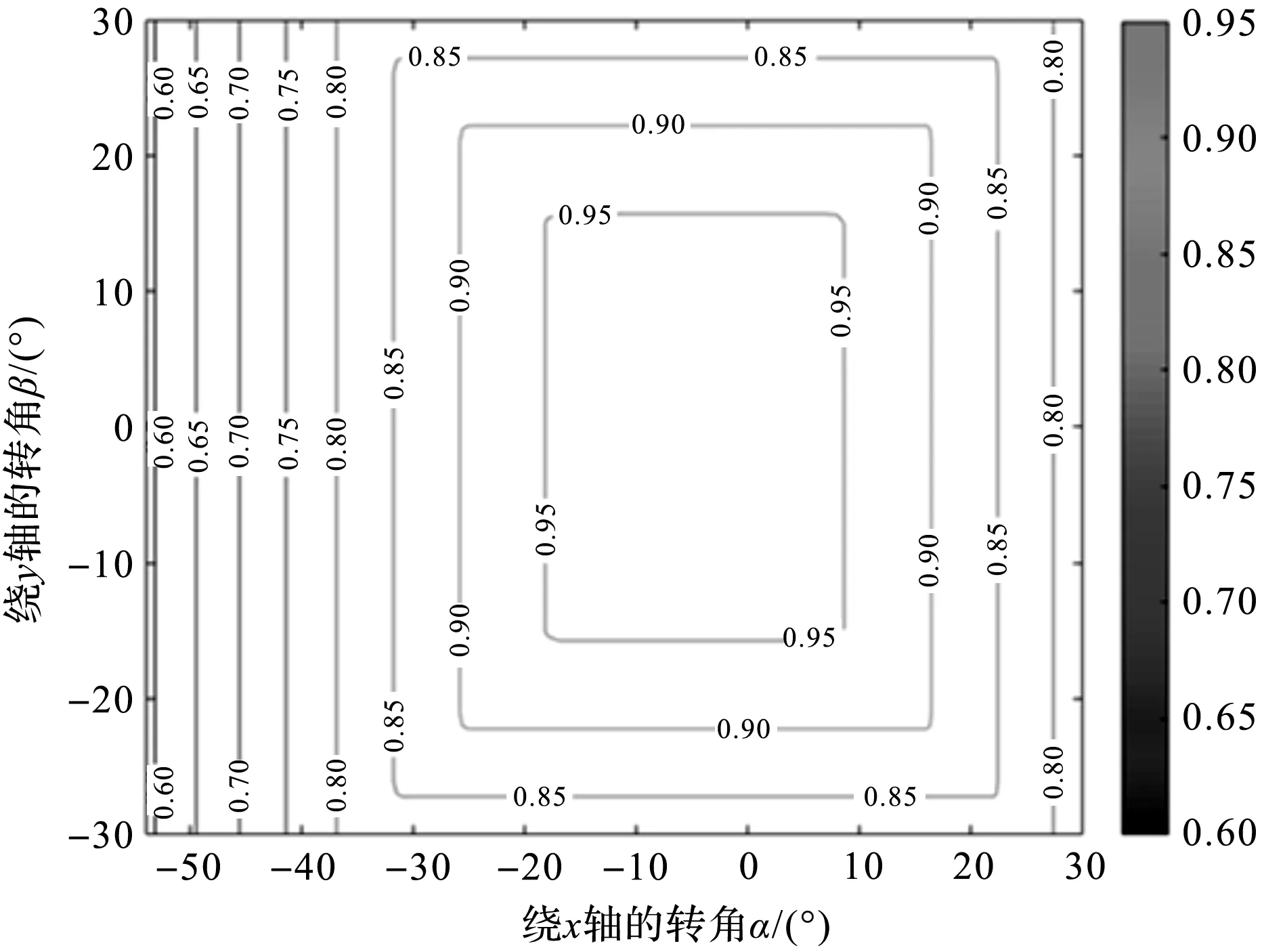
图4 机构局部传递性能分布图谱

由图4可知:机构局部传递性能(LTI)分布关于y轴对称,且中间区域的性能优于边界处的性能。初始位置时机构的传递性能最好,随着动平台角位移的增大,传递性能会随之减小;且当动平台运动到工作空间的边界时,机构的LTI的传递性能最差,其值约为0.58。

4.2 全域传递性能指标

LTI仅描述机构在某一位姿下的运动/力传递性能,而不能有效地评估机构的整体性能,为此,文献[20]提出了全域优质工作空间性能指标(GTW),以评价并联机构的整体性能,且将其定义为局部传递性能指标LTI不小于设定极限的所有位姿。

全域优质运动/力传递空间比指标为:

(27)

式中:W—机构的可达姿态空间;SG—优质工作空间的面积;S—可达姿态工作空间的面积,且Γ的取值范围为0到1(Γ值越大表示机构在姿态工作空间的优质运动/力传递空间占用比越多)。

根据表2中给出的结构参数,可计算出Γ=0.724。笔者将姿态空间内Γ≥0.8的区域定位优质传递空间。

4.3 尺度优化设计

根据运动学分析结果可知:2-RURU/RR并联机构每条分支的运动/力传递性能仅与对应分支的结构尺寸和转动关节转角参数有关,其中,影响较大的是主动杆杆长l1和l2,其次是输入角位移q1和q2。当机构位于给定空间位姿时,主动杆长与输入角位移存在唯一的关联。

根据LTI的计算公式可知:当动平台处于最大转动角位移时(α=-54°,β=30°),机构的传递性能相对较差。故在对机构的主动杆长进行优化时,分别选取动平台在两个最大边界位姿处进行分析。

选取两条分支主动杆长li的取值范围为100 mm～200 mm,可分别求得输入运动/力传递性能与主动杆长l1和l2之间的关系,如图5所示。

图5 输入力传递性能与主动杆长的关系

由图5可知:分支输入传递性能随主动杆长的增大而增强,且增长速率越来越缓慢,主动杆长li在最大位置200 mm处,机构具有更加优良的运动/力传递性能,但这也会导致机构的整机尺寸增加以及分支间干涉。

经综合考虑后,笔者取λi=0.8时所对应的主动杆长作为机构的最终尺寸,即图中虚线位置处的数值大小,得l1=140 mm,l2=150 mm。

机构主动杆长确定后,通过式(14,20),可求得初始夹角q0与机构输入传递性能指标的变化曲线,如图6所示。

图6 机构的输入传递性能与q0的关系

由图6可知:机构的输入传递性能随初始夹角q0的增大而先增大后减小,当q0=8°时。力的传递性能最好。故笔者取该机构的初始夹角q0=8°。

对于机构其他非主动杆长的尺寸设计,笔者需要先确定主动副的位置,主动副A1在o-xy平面上,主动副A2根据第2条分支的主动杆长度l2和初始夹角q0得其在y轴方向上的坐标值为20.88 mm;设定坐标系o-xyz中主动副A1在x和y轴上的坐标值分别为350 mm和300 mm,主动副A2在x和z轴的坐标值分别为410 mm和-100 mm。

机构在o-xy平面内的投影视图,如图7所示。

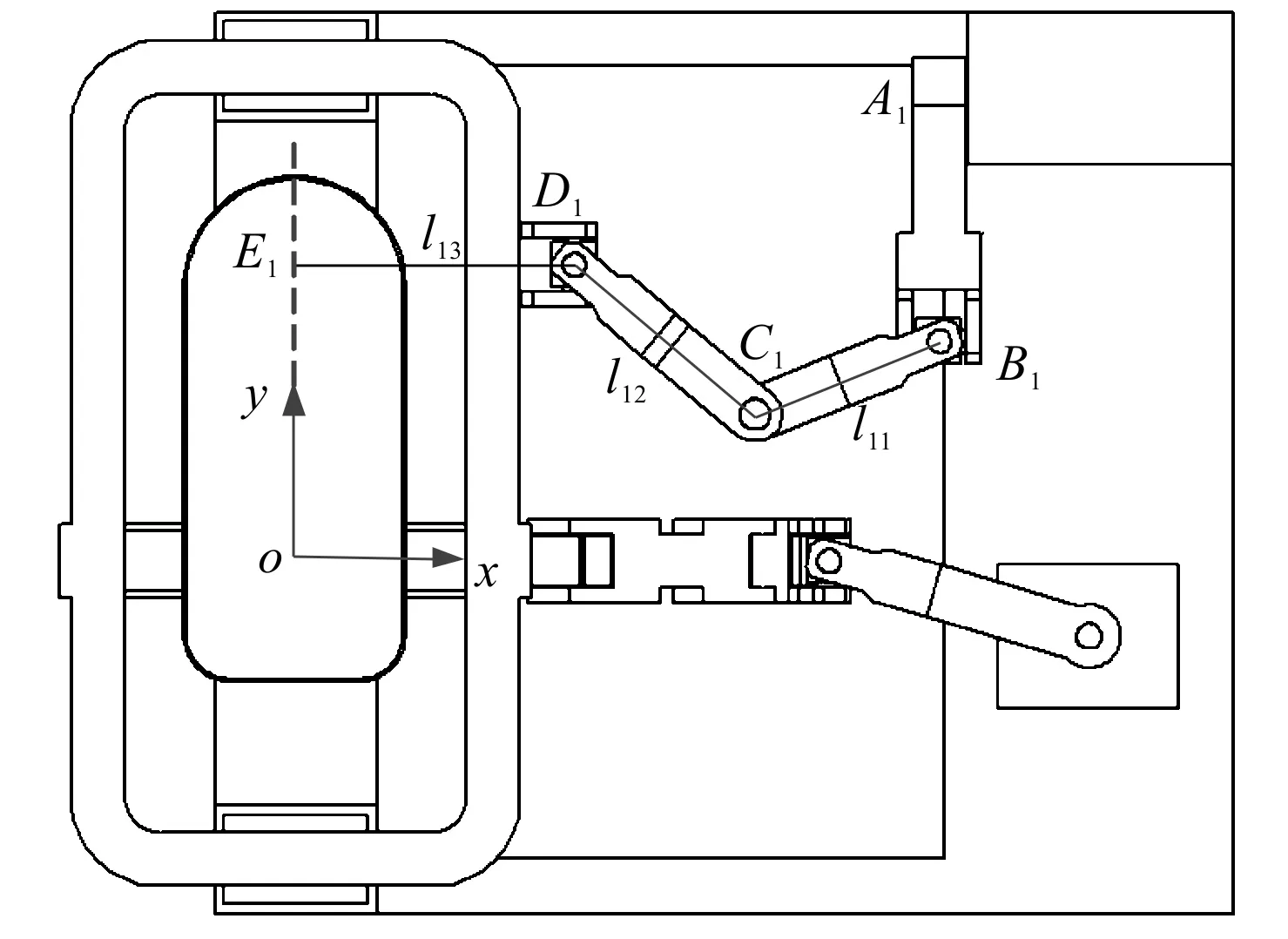
图7 机构在o-xy平面内的投影视图

由图7可知:机构的第1条分支在初始位置时,连杆l11、l12、l13与B1E1通过运动副U11、R12和U12构成特殊“平面四杆机构”,B1E1作为机架,其长度始终保持不变,杆长l13变化可视作移动副,且作为该平面机构的主动副。

同理,对于第2条分支也可通过此特征进行杆长的优化。为使得机构能够实现所需位姿,且在运动过程中不发生干涉,需使得连杆之间夹角满足对应运动副的转动范围,对于连杆l11与l12之间需满足条件:

(28)

式中:L1max—B1到y轴距离,且有L1max=350 mm。

同理,对于该平面四杆机构的其他连杆之间的夹角,即连杆l12与l13之间以及l11与机架之间,也需满足对应运动副的最大行程。

当连杆l11与l12共线时,该平面四杆机构处于死点位置,为避免该情况的出现,笔者考虑机构设计的合理性,取:

l11+l12≥1.15lB1D1

(29)

式中:lB1D1—B1、D1两点之间的最远距离,且有lB1D1=200 mm。

根据式(28,29),可求出机构第1条主动分支中非主动杆的最优尺寸。同理,也可求得机构中第2条主动分支中非主动杆长的最优解。

于是可得并联机构优化后的结构尺寸参数,如表3所示。

表3 机构优化后的结构尺寸参数

根据优化后的结构尺寸,笔者绘制出机构的全域运动/力传递性能分布图谱,如图8所示。

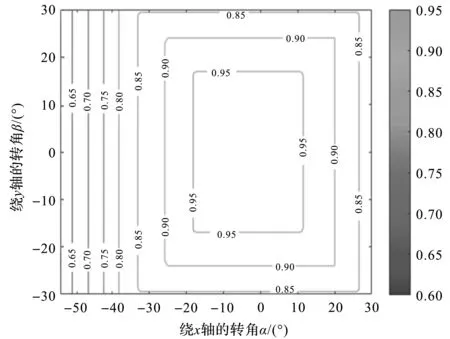
图8 优化后的全域传递性能分布图谱

由图8可知:与图4所示的优化前机构传递性能相比,优化后机构的优质传递工作空间明显增大,全域优质运动/力传递空间比指标Γ=0.832,优质传递工作空间占可达姿态空间的比例提高了10.8%。

由于机构在优质工作空间内具有良好的运动/力传递性能,这将提高踝关节康复机器人在运动康复过程中的可靠性和稳定性。

5 机器人运动学仿真及样机搭建

5.1 运动学仿真

笔者利用Solid works软件建立踝关节康复机器人的简化模型,并将其保存为Parasolid的格式,导入ADAMS中,重新定义机构各分支运动链中运动关节的约束关系,并分别在第1条和第2条主动分支运动链的主动副施加驱动。

为了保证较好的康复训练效果,机器人的运动范围应符合正常的生理结构且不能超过机构的限定范围。此时需要对主动副的输入角位移进行设定,使动平台的转动范围符合踝关节的活动度要求。

根据机构的姿态方程,即式(14),可求得主动副的运动范围,分别为q1=[-27°;27°],q2=[-36°;22°]。笔者设置仿真时间为24 s,仿真步数为200步,进行运动学仿真分析,并选取机构动平台转动中心o点作为研究对象,对该样机进行仿真分析。

仿真得到的机构动平台的角位移和角速度曲线,如图9所示。

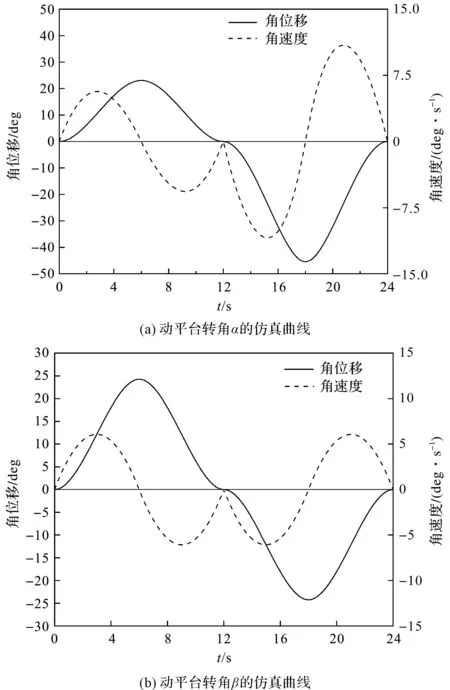
图9 运动仿真曲线

由图9可知:在运动过程中,机构各零部件间没有发生干涉和碰撞的现象;两条分支的角位移曲线反映出动平台转角β的转动范围约为-25°～25°;转角α的转动范围约为-45°～25°,能够满足踝关节的康复运动要求,并且机构的角速度曲线在运动过程中也较为平滑。

5.2 物理样机搭建

根据前述尺度优化设计,笔者得到的各条分支中连杆的尺寸,并对机构的各运动副和机架进行设计,绘制出踝关节康复机器人三维模型,如图10所示。

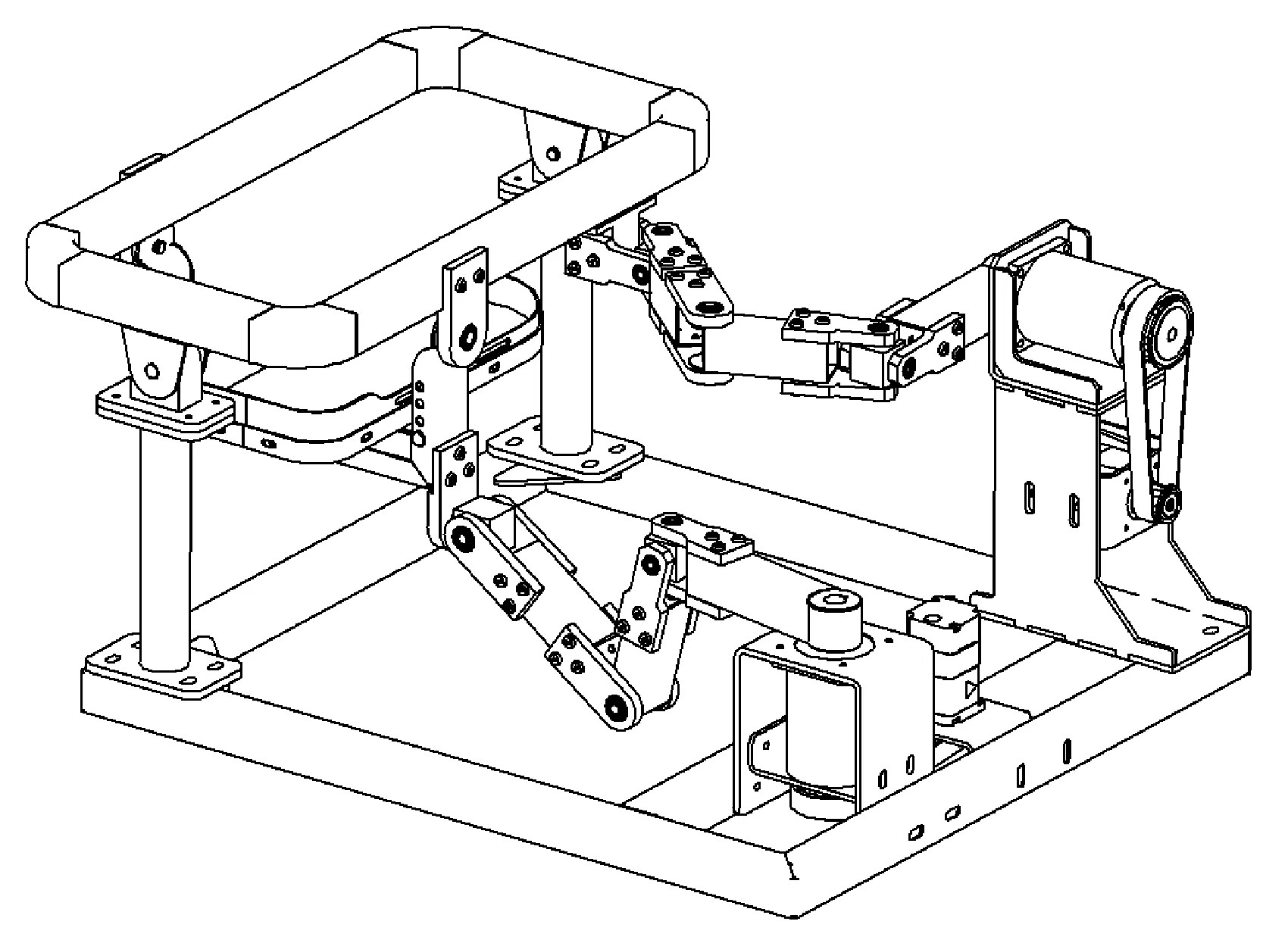
图10 踝关节康复机器人三维模型

针对不同身高、年龄的患者而言,其踝关节距离足底的高度不尽相同。为保证在康复训练过程中,人-机转动中心近似重合,笔者在动平台与脚踏板处增加了可调节装置,如图11所示。

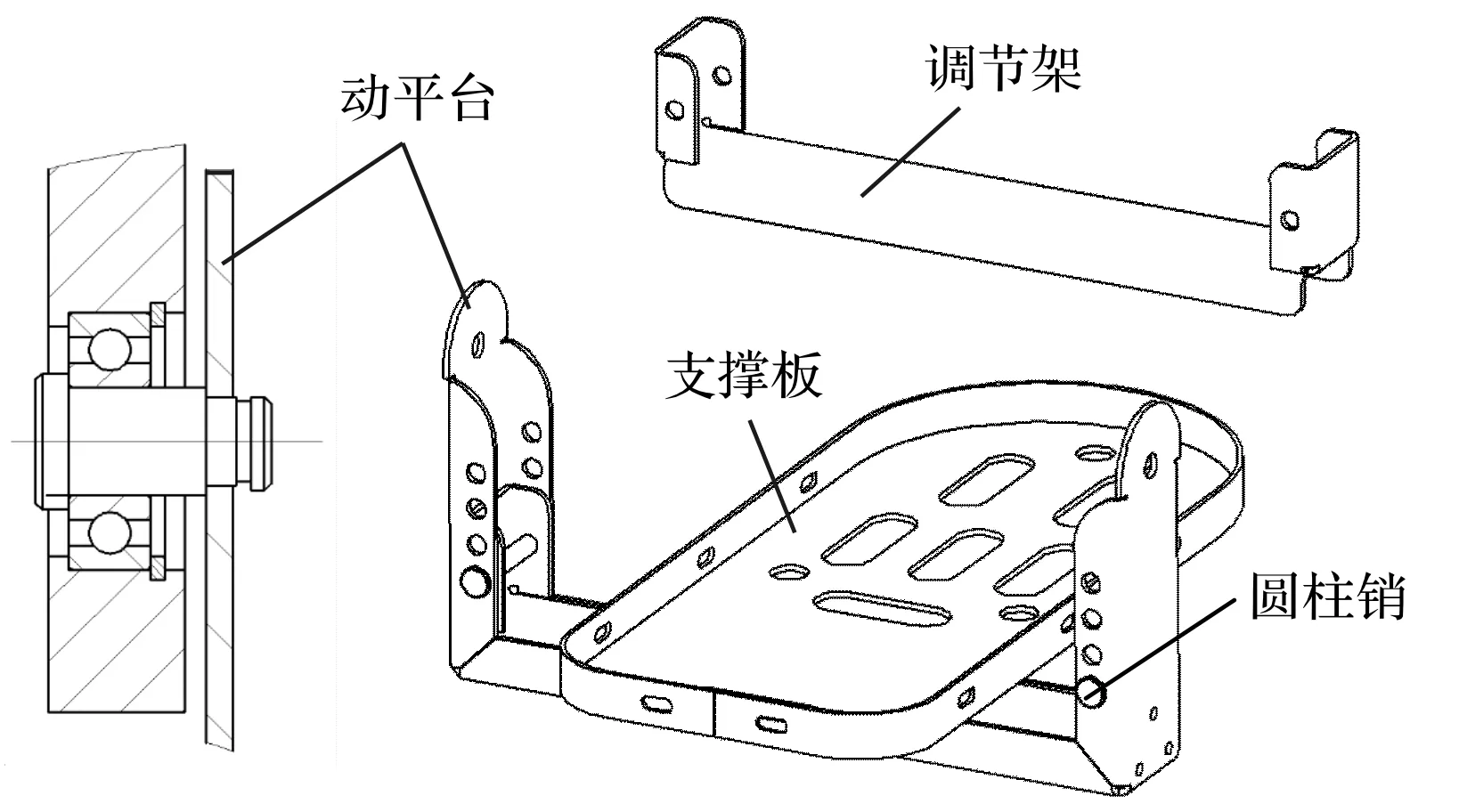
图11 踝关节康复机器人调节装置

动平台两端设有固定孔结构,通过调节架上的通孔与之配合,来调节脚踏板与机构中心的高度,从而满足不同患者的需求。

根据理论分析结果,笔者完成了机器人的物理样机搭建,如图12所示。

图12 物理样机康复运动

该处的机器人驱动模块分别采用安川公司的SGM7J-01A7A61伺服电机、SGD7S-R90A00A伺服驱动器,科峰传动KPLS070-2行星减速器;控制模块则选用固高公司嵌入式GUC-400-TPG-M23-L2型控制器。

实验结果表明:机器人在跖屈/背伸方向分别可达到53.61°和29.92°,在内翻/外翻方向分别可达到29.56°和29.19°,能够完全满足踝关节的康复训练要求。

6 结束语

针对踝关节损伤患者的康复训练需求,笔者提出了一种新型并联式踝关节康复机器人机构,建立了机构的运动学模型,基于全域传递性能传递指标对机构进行了优化设计,利用ADAMS进行了运动学仿真,搭建了康复机器人物理样机,并进行了初步的实验研究。

研究过程及结果表明:

(1)建立了踝关节康复机器人的运动学模型,推导了姿态角位移和角速度方程,机器人的速度雅可比矩阵为对角阵,故机器人具有无耦合运动学特性;

(2)基于运动/力传递性能指标对机构进行了性能分析,并通过全域传递性能传递指标对机构进行了尺度优化设计,优化后机构的优质传递工作空间占比提高了10.8%,增强了康复机器人在康复过程中的可靠性和稳定性;

(3)由运动学仿真结果可以看出,康复机器人机构动平台的角位移和角速度曲线均较为平滑,且不存在突变点,因此,该踝关节康复机器人机构具有良好的运动学性能;

(4)完成了并联式踝关节康复机器人的样机搭建,并进行了初步的实验测试,实验结果表明,机器人在跖屈/背伸方向分别可达到53.61°和29.92°,在内翻/外翻方向分别可达到29.56°和29.19°,完全能够满足人体踝关节的康复训练要求。

在后续的工作中,笔者将对踝关节康复机器人的控制策略进行研究,并根据患者踝关节的受损程度制定相应的控制策略。