基于实测挠度的PC梁桥长期预应力损失研究

卓为顶厉勇辉刘钊

（1.南京工程学院建筑工程学院，南京 211167；2.中交第二航务工程局有限公司，武汉 430040；3.中交公路长大桥建设国家工程研究中心有限公司，武汉 430040；4.交通运输行业交通基础设施智能制造技术研发中心，武汉 430040；5.东南大学土木工程学院，南京 211189）

0 引言

长期的运营实践表明，大跨径预应力混凝土变截面箱梁桥或连续刚构桥（以下简称大跨PC梁桥），普遍存在跨中下挠过大、梁体局部开裂等诸多病害［1-2］。PC梁桥产生长期下挠及开裂，可能有设计、施工、管养等多方面的原因，根本原因是局部混凝土应力的变化，如跨中底板混凝土局部可能会从受压状态逐渐转变为受拉状态。而预应力损失会导致混凝土应力的变化，与施工工艺、环境温度、荷载、混凝土收缩徐变、预应力筋松弛等有关。目前普遍认为，造成结构跨中长期下挠及混凝土开裂的主要因素是混凝土收缩徐变和成桥后长期预应力损失［3-5］。

然而，采用国内外相关规范，如《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）［6］、欧洲CEB-FIP规范［7］和美国PCI手册［8］等规范的混凝土收缩徐变模式的发展趋势是收敛的，据此计算得到PC梁桥长期挠度计算值也必然收敛，而大跨PC梁桥挠度实测值表明，长期挠度呈现不收敛的趋势［5］。预应力主要用于平衡恒载和部分活载，预应力筋的截面配筋率一般不会超过2%，且处于高应力状态；相对于混凝土收缩徐变，预应力筋的有效应力减少对结构长期下挠更加敏感。因此，可以认为长期预应力损失过大是PC梁桥过度下挠的主要因素，如1977年建成的帕劳共和国的科罗尔大桥（Koror-Babelthuap Bridge），运营18年后跨中下挠1.61 m，加固之前测得顶板预应力筋预应力损失达到50%，而设计时预测值为22%，远远超过计算预期值［9］。

目前，PC梁桥成桥后预应力损失的测量较为不便，而跨中挠度是桥梁状态的外部表征，容易进行连续的测量记录，研究跨中挠度与预应力损失的关系，可为PC梁桥的预应力设计、施工及加固评估提供依据，具有十分重要的理论和实际应用意义。

1 基于实测挠度的预应力损失计算方法

有关大跨PC梁桥长期挠度预测分析，一般采用三维实体元模型结合实测挠度数据，通过修正混凝土收缩徐变模型，预测结构长期挠度的发展趋势。美国Bažant教授采用ABAQUS三维有限元模型，将B3模型中徐变参数q2放大1.3倍、q3放大24倍、q4放大1.8倍，可得到与KB桥实测挠度数据相符的发展趋势［10］，见图1。上述计算方法未考虑裂缝造成结构刚度降低对跨中挠度的影响，且在分析过程中需要多次修正相关收缩和徐变系数，计算工作量大，计算过程较为繁琐。

图1 帕劳KB桥跨中挠度预测分析Fig.1 Deflection analysis in midspan of KB Bridge in Palau

预应力筋用以平衡恒载和部分活载，预应力损失会导致截面开裂，造成结构刚度减少。一座PC桥梁不同位置处，预应力筋张拉后有效应力相差不大，可认为预应力损失发展规律基本相同，参考CEB-FIP规范中预应力损失发展规律公式，基于观测到的挠度数据，同时考虑裂缝对结构刚度的影响，修正公式中的相关参数可以得到符合结构挠度趋势的预应力损失。

1.1 长期预应力损失计算流程

根据实测挠度数据计算桥梁长期预应力损失，需要解决两个关键问题：①建立预应力损失与截面应力关系，识别桥梁结构有效刚度；②建立预应力损失与结构长期挠度的关系，识别实测挠度点对应时刻预应力损失。本文提出基于裂缝特征参数识别结构长期预应力损失过程，见图2。

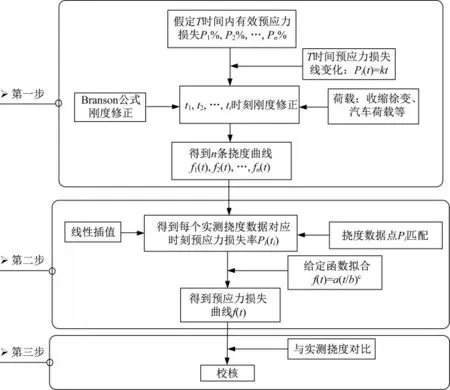
图2 基于实测挠度的长期预应力损失识别流程Fig.2 Long-term prestress loss identification process based on measured deflection

1.2 长期预应力损失计算步骤

所提出的基于实测挠度数据识别结构长期预应力损失发展规律的方法有如下特点：①该方法旨在描述预应力损失发展规律，综合考虑了施工工艺、环境温度、荷载、混凝土收缩徐变、预应力筋松弛等因素对预应力损失的影响；②该方法考虑了由于弯曲裂缝导致结构弯曲刚度下降对跨中挠度的影响，由于剪切刚度对结构挠度影响较小，可不考虑斜裂缝对剪切刚度修正；③该方法分析简单，无须建立三维实体模型和编辑子程序，采用梁单元分析即可，便于工程实践应用。

第一步：确定成桥T时间段内ti时刻的预应力损失率Pi%下的挠度曲线，具体步骤如下。

（1）假定成桥T时间段内发生Pi%预应力损失，按照线性变化：Pi(t)=kt，其中k为常数，t为计算时间，Pi(t)为预应力损失率。

（2）在T时间段内设定t1，t2，…，ti时刻，综合考虑汽车荷载、收缩徐变作用等，计算PC梁桥的中跨跨中和中墩处在t1，t2，…，ti时刻箱梁顶底板的应力。

（3）采用Branson公式对t1，t2，…，ti时刻抗弯刚度进行折减［11］，该公式实际上反映的是截面应力与截面刚度的关系，见下式：

式中：Ie为开裂截面有效惯性矩；Itr为未开裂截面惯性矩；Icr为裂缝充分开展时截面惯性矩；Ma为计算截面弯矩；Mcr为截面开裂弯矩。

Mcr/Ma也可以写成fr/fmax，公式（1）可改写为

式中：fr为开裂时截面应力，可取混凝土抗拉强度；fmax为截面外缘最大拉应力。

裂缝充分开展时截面惯性矩Icr，参照PCI设计手册［12］，可采用下式计算：

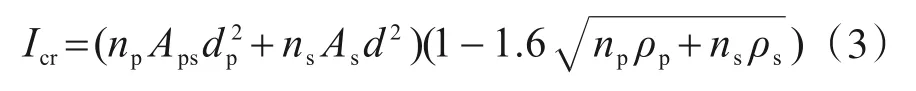
（4）计算得到考虑结构刚度修正和不同预应力损失下的挠度变化曲线，见图3。

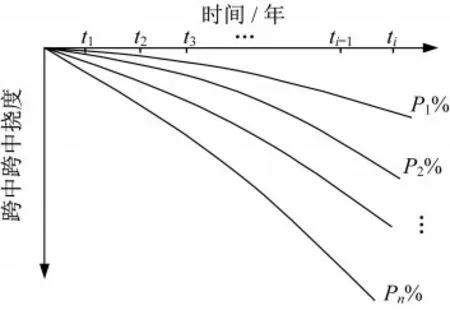
图3 不同预应力损失率下挠度曲线Fig.3 Deflection curves under different prestress loss rate

第二步：得到预应力损失变化曲线f(t)。

1）假设在时刻实测挠度数据点Pi落在fn(t)和fn-1(t)两条挠度曲线之间，实测挠度点Pi与Pn-1%挠度曲线位移差为Δi1，与Pn%挠度曲线位移差为Δi2，此时Pn-1%挠度曲线和Pn%挠度曲线时刻对应预应力损失率分别为fn-1()和fn()，如图4所示，挠度数据点Pi在时刻对应实际预应力损失率Pn()可根据与fn()和fn-1()位移线性插值取值，采用下式进行计算。

图4 实测挠度点预应力损失率计算Fig.4 Calculation of prestress loss rate at deflection point measured

2）依次得到时刻下对应的预应力损失率P1()，P2()，…，Pi()，参考CEB-FIP中预应力损失规律，修正对应参数a、b、c进行拟合，如下式所示：

式中，a、b、c均为常数。

第三步：通过实测挠度拟合得到预应力损失随时间发展的相关曲线。参考第一步，得到拟合预应力损失曲线f(t)挠度曲线，并与实测挠度曲线对比。

2 实桥验证

以广东省虎门大桥辅航道连续刚构桥为例［13］，通过该桥多年连续观测挠度数据推算预应力损失发展规律，并与实测挠度趋势对比，验证上述方法的可行性。

2.1 虎门大桥辅航道桥基本信息

虎门大桥辅航道桥为预应力混凝土箱梁连续刚构桥，跨径布置为（150+270+150）m，桥型布置见图5，中墩处截面梁高为14.8 m，腹板厚度为0.6 m，中跨跨中截面梁高为5 m，腹板厚度为0.4 m，关键截面尺寸见图6。该桥于1997年6月建成通车，通过多年的连续挠度观测，发现中跨跨中挠度呈现持续增长的趋势，远远超过设计值，见图7。

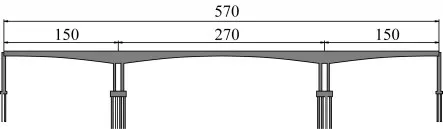
图5 虎门大桥桥跨布置（单位：m）Fig.5 Span layout of Humen Bridge（Unit：m）

图6 箱梁的I-I/II-II断面（单位：cm）Fig.6 Section I-I/II-II of the box-girder（Unit：cm）

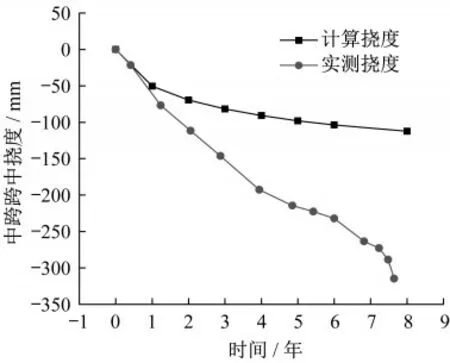
图7 实测挠度与计算挠度对比Fig.7 Comparison between the measured deflection and calculated deflection

2.2 虎门大桥辅航道桥预应力发展规律识别

采用Midas Civil有限元软件建立三维有限元模型，对虎门大桥辅航道桥成桥后挠度进行数值分析，见图8。施工过程中共考虑35个施工节段，施工持续417天。

图8 虎门大桥辅航道桥三维有限元模型Fig.8 3D finite element model of the auxiliary channel bridge of Humen Bridge

以虎门大桥辅航道桥为例，对该桥成桥8年内的挠度值进行分析。对该桥成桥后预应力损失计算的具体步骤如下。

第一步：确定成桥8年内不同预应力损失率Pi%下的挠度曲线。

假设从桥开始到成桥8年期间内分别完成5%、10%、15%、20%、25%、30%、35%的预应力损失，通过式（2）和式（3）修正刚度后，计算可得不同预应力损失下的挠度发展曲线，见图9。

图9 虎门大桥辅航道桥不同预应力损失下挠度曲线Fig.9 Deflection curves of the auxiliary channel bridge of Humen Bridge under different prestress losses

第二步：确定预应力损失变化曲线f(t)。

对虎门大桥辅航道桥左幅成桥8年内12次挠度测量数据进行分析，受季节温度和温度梯度的影响，实测挠度数据略有波动。根据整体挠度数据呈直线下降的趋势，采用线性函数对这12次数据进行修正，见图10。

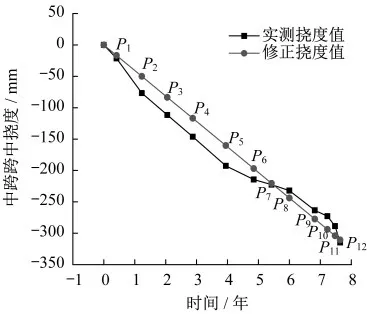
图10 虎门大桥辅航道桥实测挠度数据修正Fig.10 Correction of deflection data measured of the auxiliary channel bridge of Humen Bridge under different prestress losses

（1）根据挠度测点时间，将挠度测点分别匹配到图9中，见图11。

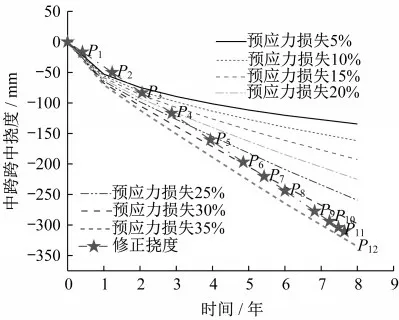
图11 虎门大桥辅航道桥挠度测点区间匹配Fig.11 Matching among the measured deflection points of the auxiliary channel bridge of Humen Bridge

（2）根据每个测点与其相临两个挠度曲线位移差，采用式（4）计算得到每个测点对应时间的预应力损失率Pi(t~i)，各挠度测点对应时间下预应力损失率见表1。

表1 挠度测点对应时间下预应力损失率Table 1 Prestress loss rate of steel strands at the measured deflection point at corresponding time

（3）以式（5）对12个挠度数据点相应时间下的预应力损失率进行拟合，得a=5.61×10-3，b=15.56，c=1.62，见图12。

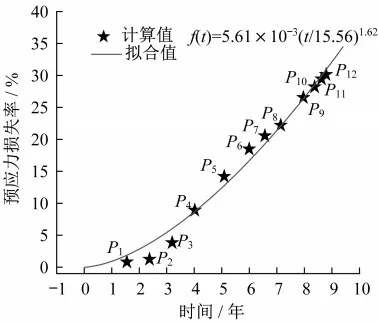
图12 预应力损失率曲线拟合Fig.12 Fitting the curve of the prestress loss rate

第三步：将拟合曲线的数值代入第一步，修正刚度后计算得到在预应力损失曲线f(t)下的挠度曲线，并与实际挠度曲线对比，校核所拟合曲线的正确性，见图13。

由图13可看出，采用拟合得到的预应力损失发展曲线f(t)通过计算得到结构挠度，能较好反映结构实际挠度发展趋势。

图13 计算挠度和实测挠度对比分析Fig.13 Comparison analysis on calculated deflection and measured deflection

3 结论

PC梁桥在长期运营后，常会造成中跨跨中下挠过大且不收敛，主要原因是预应力损失持续发展且远大于预期值。本文通过开展预应力长期损失发展规律的研究，得到如下结论：

（1）提出了一种基于实测挠度数据计算成桥后预应力损失的方法，给出了计算步骤和流程，考虑了开裂后梁体刚度折减。

（2）给出了混凝土开裂后的梁体刚度折减公式，建立了时间-预应力损失率-实测挠度的关系，计算过程简单，便于工程实践应用。

（3）以虎门大桥辅航道桥为例，基于该桥成桥后8年的实测挠度数据，计算其预应力损失的发展过程，验证了所提出计算方法的可行性。