加载角度对弧形加载巴西劈裂试验影响的数值研究

孙志伟包春燕，2，*蔡悦翔

（1.绍兴文理学院土木工程学院，绍兴 312000；2.绍兴文理学院岩石力学与地质灾害实验中心，绍兴 312000）

0 引言

目前，测量岩石抗拉强度的方法主要有两种［1-6］：直接拉伸试验和巴西劈裂试验。研究者们普遍认为，直接拉伸试验的结果更接近岩石的真实抗拉强度。然而，由于直接拉伸试验试件加工难度大，而且不可避免会出现偏心加载，导致力的作用线与试样中心轴不重合。因此，相较于直接拉伸试验，测试岩石抗拉强度时巴西劈裂试验更为常用。

传统巴西劈裂试验（图1）对圆盘施加径向相对的集中载荷，由于端部应力集中，会在端部加载处附近先发生压破坏，而不是在中心处产生拉破坏，得到的名义抗拉强度与真实值误差较大［7］。为满足巴西劈裂试验中心起裂的要求，减少应力集中，研究者们提出将集中加载改为弧形加载或平台加载。平台加载法于2002年首次由王启智等［8-12］提出用于测定岩石抗拉强度，但是其削去圆盘的一部分，改变了圆盘的形状，破坏了圆盘的整体性，圆盘受压是否均匀，是否依旧符合弹性理论，结果是否可靠，还有待进一步验证。如图2所示，相较于集中加载巴西劈裂试验，弧形加载试验通过改变压头垫块形状等方式，将对试件端部施加的一对集中载荷均匀地分布在具有一定长度的弧线上形成弧形荷载，该弧线所对应的圆心角2α即为加载角度。弧形加载法能改善加载处的应力状态，使试件端部均匀受压，避免应力集中，满足了中心起裂的要求，结果可靠度高，被众多学者认可［2，13-15］。

图1 集中加载巴西圆盘力学模型Fig.1 Mechanical model of Brazilian disk under concentrated loading

图2 弧形加载巴西圆盘力学模型Fig.2 Mechanical model of Brazilian disk under arc loading

目前，试验相关的标准规程如《水利水电工程岩石试验规程》（SL 264—2001）［16］、《工程岩体试验方法标准》（GB/T 50266—99）［17］等都只对巴西劈裂法的试件直径、厚径比和荷载施加速率给出了一定范围的规定，但是没有给出规定的加载角度，导致巴西劈裂试验测得的抗拉强度值表现出极大的离散。本文对不同加载角度下的弧形加载巴西试验进行研究，将会是对相应研究的有益补充，为加载角度的选取提供理论依据，对于推动岩石力学基础研究的发展将产生深远的意义。

考虑到由于多个不同角度的弧形加载巴西劈裂试验不存在理论解，多组不同角度的弧形压头实际操作困难，并且实际试验时垫块与试件之间存在摩擦会对结果产生较大影响，因此本文采用数值模拟的研究方法，既能排除摩擦的影响，又能够直观地反映巴西圆盘内部的应力场和位移场。

1 巴西劈裂试验理论解

巴西劈裂试验的标准规程中规定的圆盘试件厚径比为0.5～1.0，因此当圆盘试件属于弹性变形时，可将三维问题简化为二维平面问题，根据弹性理论可以得到圆盘内任意一点的应力理论解。1958年Н.И.Мусхелишвили［18］采用复变函数的方法给出了精确描述集中力加载下的传统巴西圆盘内任意一点的应力解析解。直径为D、厚度为t的传统巴西劈裂圆盘试件在一对集中力P加载下的力学模型（图1）和圆盘内任意一点A（x，y）的正应力σx、σy及剪应力τxy的表达式如下所示：

将x=0，y=0代入式（1）中，可得圆盘中心点O处的应力解析解如下：

通常岩石类材料的抗拉强度是抗压强度的0.1倍以下［1］，由式（2）可知，σx0＞0.1σy0，说明圆盘中心处的拉应力先达到抗拉强度发生拉伸破坏，即中心先起裂。当施加的荷载P达到试件材料破坏时的临界荷载Pt，此时的σx0即为所测的抗拉强度σt。

2 数值模型及结果验证

2.1 数值模型及相关参数

为证明数值模拟的可靠性，本文采用有限元软件ANSYS首先建立加载角度2α为0°的集中加载模型，根据试验相关的标准规程取圆盘试件直径D=50 mm，厚度t=25 mm，弹性模量E=40 GPa，泊松比μ=0.25；由于上、下垫块与圆盘试件相切，因此垫块宽度不影响试验结果，取与试件直径相同值为50 mm，取弹性模量E=4 000 GPa，泊松比μ=0.25，可认为是刚体；上、下垫块与圆盘试件之间光滑无相对滑动，摩擦系数为0。ANSYS建模采用具有拉裂和压碎性能的Solid65单元类型，网格单元采用误差较小的六面体单元进行划分，在上垫块上表面中心施加竖直相下的集中力P=1 kN，下垫块下表面节点约束。

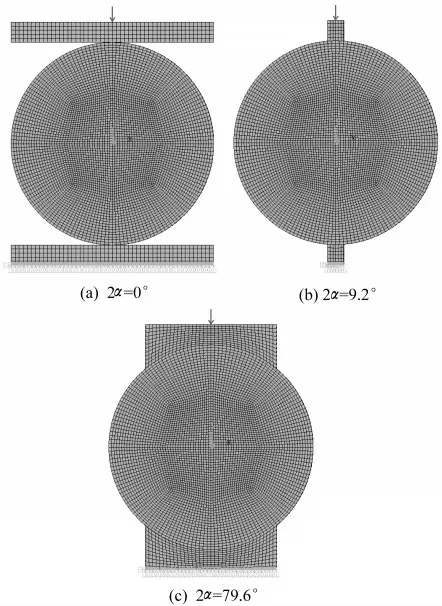
图3 部分不同加载角度的巴西劈裂模型Fig.3 Parts of the Brazilian splitting numerical model with different loading angles

之后再以集中加载模型为原型分别建立不同加载角度的弧形加载模型，研究加载角度对弧形加载巴西劈裂试验的影响。通过改变垫块的宽度控制加载角度，为更明显地观察加载角度导致的试件由受拉破坏向受压破坏过渡的过程，垫块宽度取较大的范围为2～32 mm，其所对应的加载角度2α分别为9.2°，13.8°，18.4°，23.1°，27.8°，32.5°，37.3°，42.2°，52.2°，62.7°，79.6°。

2.2 集中加载模型数值解与理论解对比

由于模型结构和荷载均对称，因此取圆盘上半部分进行分析，分别计算出集中加载（即加载角度2α=0°）下圆盘加载直径上半段（即图1中OB段）上点的应力数值解与理论解，对比以证明数值模拟结果的可靠性。

观察图4可知，圆盘加载直径上点的水平应力σx和垂直应力σy数值解和理论解的变化曲线仅在靠近加载点附近出现较大分离，而在远离加载点处基本重合。圆盘加载直径上点的水平应力σx和垂直应力σy的数值解普遍小于理论解，水平应力σx的理论解与距圆心的距离y无关，为一固定值，而数值解随着距圆心的距离y增加而减小，逐渐由正变负。

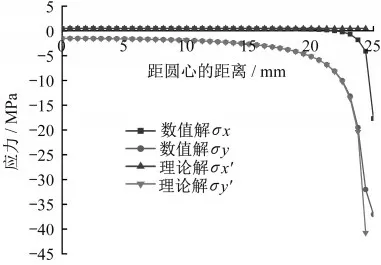
图4 集中加载模型中轴线应力数值解与理论解Fig.4 Numerical and theoretical solutions of axial stress in concentrated loading model

通过表1可知，水平应力σx和垂直应力σy的数值解与理论解的误差随着距圆心的距离y增加而增大，在靠近圆盘中心处较小，在靠近加载点附近误差较大。由于应力集中的原因，普遍认为靠近加载处的部分结果不可靠，因此主要分析靠近圆心部分的结果。当y≤20 mm时，垂直应力σy数值解与理论解的最大误差为1.3%、最小误差为0.14%，水平应力σx数值解与理论解的最大误差为36.02%、最小误差为1.79%，考虑到靠近加载点附近应力集中的原因，可认为均属于合理误差，因此证明该模型能够较好地模拟出巴西圆盘劈裂试验。

表1 集中加载模型中轴线应力数值解与理论解误差Table 1 Error between numerical solution and theoretical solution of axial stress in concentrated loading model

3 加载角度的影响分析

3.1 加载角度对中轴线上应力分布的影响

在不同加载角度的弧形加载模型中，圆盘试件中轴线上半段上点的水平应力结果如图5所示。从图5中可以看出，所有模型中的水平应力σx的最大值皆出现在圆盘中心处，圆盘中心附近水平应力为正值，表现为拉应力，随着位置从中心向加载处推移，水平应力逐渐减小变为负值，拉应力过渡为压应力，由于加载造成的局部应力集中，在靠近加载处表现为极大的压应力。同时发现，随着加载角度2α的增大，巴西圆盘中轴线上的水平拉应力σx缓慢减小，最大水平拉应力从加载角度2α为0°时 的0.50 MPa降 低 到80°时 的0.32 MPa，而最大水平压应力却从4.10 MPa急降到1.95 MPa。

图5 不同加载角度模型中轴线水平应力结果Fig.5 Horizontal stress results of axis in model with different loading angles

把水平应力变化曲线与坐标轴交点之间的区域称之为拉应力区［8］，其余区域称为压应力区。图6给出了中轴线上半段压拉应力临界位置随加载角度的变化曲线，能直观地看出拉应力区的变化情况。随着加载角度的增大，圆盘中轴线上的拉应力区逐渐减小，压应力区增大。由图6可见，随着加载角度的增大，圆盘中心点压拉应力比增大，当加载角度2α从0°增加到80°时，圆盘中心点压应力与拉应力之比从3.02增加至4.37。

图6 中轴线上压拉应力临界位置随加载角度变化曲线Fig.6 The curve of the critical position of compressive and tensile stress along the central axis with the loading angle

加载角度2α的增大导致压应力作用加强，圆盘试件的破坏不再单纯是由于圆盘中心处的拉应力先达到抗拉強度而发生拉伸破坏，而是向压、拉应力共同作用下发生的复杂破坏模式过渡。当加载角度2α＜27.8°时，压拉比随加载角度2α变化较缓，此时仍是拉破坏为主；但当加载角度2α＞27.8°时，曲线变得陡峭，压拉比的增大趋势随加载角度2α增加而加剧，拉应力的作用相对减小，压应力作用加强，表现出明显的复杂破坏模式，此时圆盘达到破裂状态所需的临界载荷值增大，计算得到的名义抗拉强度随之增大。因此，采用弧形加载巴西劈裂试验测定岩石抗拉强度时，加载角度2α不宜超过27.8°。

图7 圆心点压拉比随加载角度变化曲线Fig.7 Variation curve of compression ratio at center point with loading angle

3.2 加载角度对圆盘破坏模式的影响

表2给出了不同加载角度模型圆盘内的最大压拉应力，表中最大拉应力点均位于圆盘中心处。当加载角度2α＜37.3°时，最大压应力点位于加载圆弧端点附近；当加载角度2α＞37.3°时，最大压应力点位于加载圆弧中点附近。

一般来说，岩石类材料的抗压强度与抗拉强度的比值普遍为8～10，表2中集中加载巴西劈裂试验圆盘内的最大压拉应力比为63.99，远大于此范围，表明圆盘此时是由于加载点附近压应力先达到其抗压强度发生压破坏，而并非是圆盘中心处的拉应力先达到抗拉强度度发生拉破坏，因此集中加载巴西劈裂试验不适合用来测试岩石抗拉强度。而弧形加载巴西劈裂试验随着加载角度增大，最大压应力显著减小，其值从加载角度2α为0°时的32.00 MPa降低到79.6°时的1.57 MPa，同时圆盘内的最大压拉应力比会随着加载角度增大而减小，当加载角度2α为18.4°时，其最大压拉应力比已经降低到9.74，此时可认为巴西圆盘试样不会发生加载处的压破坏而是发生中心拉破坏，满足巴西劈裂试验中心起裂条件。

表2 不同加载角度模型圆盘内最大压拉应力Table 2 Maximum compressive tensile stress in model disk with different loading angles

综上可知，加载角度是影响巴西劈裂试验结果的关键因素，加载角度选取不当会极大地影响试验所测的验抗拉强度值，加载角度过小，不能保证试件中心起裂；加载角度过大，试验向单向压缩过渡，测的可能是抗压强度，而不是抗拉强度。结合前文综合考虑能够同时满足中心起裂、降低应力集中程度和圆心点压拉比增长缓慢的要求，弧形加载巴西劈裂试验的最优加载角度2α的范围为18.4°～27.8°。

4 巴西劈裂试验抗拉强度修正公式

目前巴西劈裂试验相关的标准规程［16-17］给出的抗拉强度计算公式为式（3），喻勇［19］曾指出该抗拉强度公式是由二维弹性力学公式推导而出，与三维实际情况存在一定误差，因此本文在该公式的基础上提出抗拉强度修正系数k得到式（4），修正系数k为施加荷载总值相等的条件下不同加载角度巴西圆盘中心点水平应力数值解与集中加载巴西圆盘中心点水平应力理论解的比值，即式（5）。

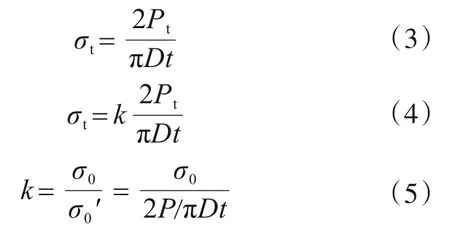
式中：σt为巴西劈裂试验所测抗拉强度；Pt为巴西劈裂试验中圆盘破裂时所施加的荷载；D为圆盘试件直径；t为圆盘试件厚度；σ0为巴西圆盘中心点水平应力数值解；σ0′为集中加载巴西圆盘中心点水平应力理论解；P为巴西劈裂试验数值模拟和理论计算时所设的荷载。

图8为巴西劈裂试验抗拉强度修正系数k随加载角度2α变化的曲线，曲线的变化率随加载角度2α的增大而减小，显然加载角度2α越大，修正系数k越小，且减小的幅度也越明显。当加载角度2α=18.4°时，修正系数k=0.974；当加载角度2α=27.8°时，修正系数k=0.951。因此当采用推荐的加载角度2α为18.4°～27.8°的弧形加载巴西劈裂试验测试岩石抗拉强度σt时，抗拉强度修正系数k为0.951～0.974。

5 结论

（1）集中加载巴西劈裂试验靠近圆心部分的应力数值解与理论解误差较小，表明数值模拟能够较好地模拟出巴西圆盘劈裂试验。

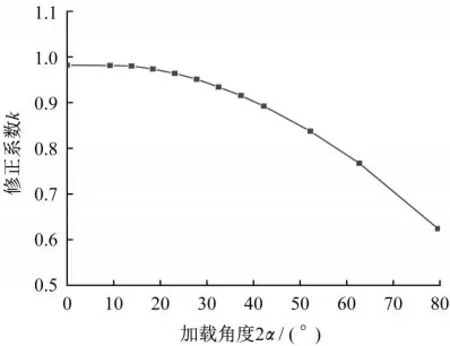
图7 抗拉强度修正系数随加载角度变化曲线Fig.7 Curve of tensile strength correction coefficient with loading angle

（2）随着加载角度2α的增大，巴西圆盘中轴线上的水平拉应力σx减小，圆盘轴线上拉应力区减小，压应力区增大，圆盘中心点压拉应力比增大。当加载角度2α＜27.8°时，圆盘中心点压拉比变化较小，以拉破坏为主；当加载角度2α＞27.8°时，圆盘中心点压拉比变化较大，拉应力作用减小，压应力作用加强。

（3）圆盘内的最大压拉应力比随加载角度增大而减小。当加载角度2α＜18.4°时，最大压拉应力比大于10，加载点附近压应力过大，发生压破坏，不满足中心起裂的要求；当加载角度2α＞18.4°时，最大压拉应力比小于10，圆盘试样满足巴西劈裂试验中心起裂条件。

（4）综合考虑弧形加载巴西劈裂试验的最优加载角度2α范围为18.4°～27.8°。提出抗拉强度修正系数k，其值随加载角度2α的增大而减小，最优加载角度对应的抗拉强度修正系数k范围为0.951～0.974。