大跨人行景观桥的人致振动控制研究

王言泽 施卫星

（同济大学结构防灾减灾工程系，上海 200092）

0 引言

随着城市的快速发展，人行桥结构趋向于大跨度化。与此同时，高强轻质材料的涌现使人行桥结构变得轻柔化、低阻尼化，行人行走在人行桥结构时，人行桥结构在步行荷载作用下产生振动响应。当行人行走步频接近于人行桥结构固有频率时，容易引起人行桥大幅振动，将行人步行荷载导致人行桥结构发生的振动称为人致振动［1］。近年来，国内外出现人行桥发生较大的人致振动，不仅严重影响桥上行人行走舒适度，甚至还影响到人行桥结构安全和正常使用。已有研究成果表明：竖向振动基频低于5 Hz，侧向振动基频低于1.4 Hz的人行桥均有可能发生人桥共振［2］。

调谐质量阻尼器（Tuned Mass Damper，TMD）是很好解决大跨结构振动的方法。近年来，随着TMD研究越来越成熟，大量工程开始采用TMD作为减振措施［3］。TMD减振系统构造简单，由质量块、弹簧和阻尼三部分组成。TMD附加在主体结构外的动力系统，其质量和弹簧一起构成振动吸收装置，而增加的幅值通过减振系统中的阻尼将能量耗散。吕西林等［4］通过有限元模拟和现场实测的方法研究了上海世博文化中心（长悬臂空间结构）采用TMD的人致振动控制问题。严俊等［5］研究了楼盖结构在不同工况人行荷载作用下安装TMD系统前后的振动响应。操礼林等［6］提出了基于人行天桥自身动力参数时变的TMD减振设计方法。王梁坤等［7］提出自适应多重TMD减振系统，并研究其频率自适应调节的鲁棒性。

本文以国内某在建的大跨景观人行桥为背景，并利用MIDAS有限元软件进行建模，分析了该桥的自振特性和人致激励下结构的动力时程响应，并对比分析了该人行天桥增加TMD减振系统后，在相同人致振动下的动力时程响应，验证了TMD减振系统对该大跨景观人行桥结构振动控制的有效性，并为类似天桥减振设计提供借鉴。

1 大跨景观人行桥的模态分析

1.1 大跨景观人行桥的动力特性分析

该大跨景观人行桥是一个环状结构，结构形式为空间钢桁架，并由32根支承柱支承，该大跨人行景观桥高为6.2 m，环内有两处连接地面。人行景观桥概念图如图1所示。

图1 人行景观桥概念图Fig.1 Conceptual diagram of pedestrian landscape bridge

本文采用目前结构设计常用的有限元分析软件MIDAS建立三维模型进行分析，建立的人行桥模型如图2所示。

图2 人行景观桥结构模型图Fig.2 Structural model of pedestrian landscape bridge

人行桥的自振特性反映了其振动的固有属性。本文在结构的模态分析中，振型数目取为50，使用利兹向量法进行整体的模态分析。取该人行桥的前10阶自振频率和其振型质量参与系数，如表1所示，利用MIDAS进行有限元模态分析，结果表明，该人行景观桥的竖向振动主要集中在第一阶振型即整体振动第一振型。结构频率为1.17 Hz，竖向振型质量参与系数为18.75%。行人竖向一阶步频1.2～2.8 Hz，当人行景观桥接近接近行人正常步行频率，还是有可能引起较大的共振，所以需要进行动力时程分析和舒适度分析。该结构第1阶竖向振型图如图3所示。

图3 人行景观桥的第一阶竖向振型图Fig.3 The first vertical mode of pedestrian landscape bridge

表1 人行景观桥结构动力特性Table 1 Dynamic characteristics of pedestrian landscape bridge structure

由图2可见，在竖向第一阶振型中，椭圆环最长跨的跨中处竖向振动最明显。

1.2 人行荷载模型及工况设置

行人的行走可能产生垂直荷载、横向荷载以及纵向荷载。而人致振动产生的横向和纵向荷载幅值相对竖向很小，一般不会引起人行桥的共振，所以在舒适度分析时不予考虑。本文人行荷载可以按照行走频率和人群密度进行分类。行人较少时，可以自由行走，故步频较大，跑动时可以达到3.5 Hz。而当人数较多时由于比较拥挤，行人的步伐可能趋于一致，此时步频比较低，且行人之间的协同作用增强［8］。为综合判断各种行走工况下的景观桥振动情况，设计时共计考虑了6种工况，包括《建筑楼盖舒适度设计规范》［9］推荐的5种工况以及1个共振工况。在对行人人数进行等效时，需要考虑人群密度的影响，根据人行面积计算并根据德国人行桥设计规范EN03［10］中人数折减公式（1）得到各种行走工况下的等效人数，本节选取的时程分析工况如表2所示。

表2 时程分析工况定义Table 2 Definition of time history analysis conditions

式中：ξ为舒适度分析时的结构阻尼比，本结构中取值为0.02；N为行人总人数；m为等效行人人数。

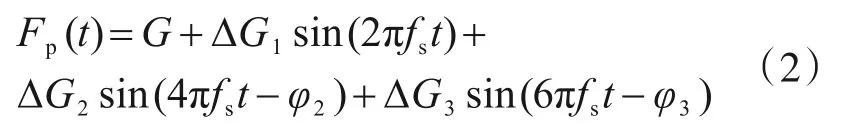
对人行景观桥进行非线性时程分析时，单人连续行走的荷载时程函数由Bachmann等［11］在1987年提出的式（2）表示，该人行景观桥振动最明显的一跨，宽度6.6～10 m，长约80 m，面积约为650 m2，荷载以集中荷载形式，施加到人行桥面板节点上，从而激励人行景观桥的振动。式中：G为人的自重（一般为800N）；ΔG1为波激励的一阶分量，当fs=2 Hz时取值0.4G，fs=2.4 Hz时取值0.5G，之间采用线性插值；ΔG2为谐波激励的二阶分量，取值为0.1G；ΔG3为谐波激励的三阶分量，取值为0.1G；fs为行人的步频；φ2为二阶谐波相对于一阶谐波的相位角，一般可取值为π/2；φ3为三阶谐波相对于二阶谐波的相位角，一般可取值为π/2。

1.3 舒适度评估指标

人体对于结构振动而感受到的舒适度存在较大的主观性，所以舒适程度并不能定量评价。各国人行桥设计规范从加速度限值方面对振动舒适度问题作出了相应的规定。欧洲规范EN1990［12］规定竖向振动加速度限值为70 cm/s2，德国规范EN03［10］规定竖向振动加速度限值为50 cm/s2，而我国2019年发布的《建筑楼盖舒适度设计规范》［9］中，不封闭连廊的竖向振动加速度限值为50 cm/s2，本文的人行景观桥对舒适度的要求参考不封闭连廊，取竖向振动加速度限值为50 cm/s2。

1.4 人行景观桥动力时程响应分析

我国在《城市人行天桥与人行地道技术规范》（CJJ 69—95）［13］中为避免人行桥共振问题，规定一阶竖向频率必须要大于3 Hz。本文中的人行景观桥一阶竖向频率为1.17 Hz，不符合规范要求。对6种工况进行动力时程分析，在不加设TMD减振系统的情况下，检验该人行景观桥是否满足舒适度规范要求，得到6种工况分析的结果如表3所示。在TC6工况下，竖向最大加速度51.64 m/s2，超过了规范对舒适度限值50 cm/s2，需要设置TMD减振系统进行减振控制。

表3 加设TMD前各工况结构时程响应Table 3 Time history response without TMD

2 TMD减振系统的设计与分析

2.1 TMD的参数设计

该人行景观桥整体连廊的质量为1 529 t，竖向一阶振型参与质量约为286 t，质量比取值为2.1%，对于该结构而言，最长跨跨中竖向振动最为明显，在该区域布置TMD对竖向振动控制效果最好，该区域共计布置5个TMD，每个质量为1.2 t，频率均为1.17 Hz，其详细布置位置见图4，TMD参数表如表4所示。

图4 TMD布置位置图Fig.4 TMD layout drawing

表4 TMD参数表Table 4 Parameter of TMD

该人行桥加设的TMD-I减振系统如图5所示。

图5 TMD的渲染图Fig.5 Rendering of TMD

2.2 TMD减振效果分析

利用MIDAS有限元分析软件再次对加设TMD减振系统的人行景观桥进行动力时程分析，取该人行桥的前10阶自振频率和其竖向振型质量参与系数如表5所示。

表5 减振结构自振频率与竖向振型质量参与系数Table 5 Frequencies and vertical modal participating mass ratios with TMD

2.3 加设TMD后的振动舒适度评价

本文采取评价振动舒适度的指标为竖向加速度峰值，表6结果显示了人行景观桥振动最剧烈的节点上的竖向加速度，通过比较未加设TMD结构和加设TMD结构的竖向加速度的变化，并以此评价TMD的减振效果。动力时程分析的结果对比如表6所示。

表6 减振前后动力时程分析结果Table 6 Dynamic time history analysis results without/with TMD

通过表6可以发现，行人以1.17 Hz运动时，且人行景观桥非常拥挤的情况下，加设TMD减振系统后，结构减振效果达到27.8%。人行景观桥的竖向最大加速度为37.30 cm/s2，小于规范对舒适度限值50 cm/s2，满足振动舒适度标准。图6和图7分别表示6种工况的跨中节点减振前后的加速度时程曲线对比。对比发现，加设TMD减振系统后，结构减振效果明显。

图6 减振前各工况跨中节点竖向加速度时程曲线Fig.6 Vertical acceleration time history of mid-span node in each working condition before vibration reduction

图7 减振后各工况跨中节点竖向加速度时程曲线Fig.7 Vertical acceleration time history of mid-span node in each working condition after vibration reduction

3 结论

本文以国内某在建人行景观桥为背景，依据《建筑楼盖舒适度设计规范》［9］推荐的5种工况以及1个共振工况及人行荷载模型，进行了原结构和加设TMD减振系统后结构的动力时程分析和舒适度评价，主要得出如下结论：

（1）通常人行荷载的频率范围为1.2～2.8 Hz，而人行景观桥结构的竖向第一阶振型频率为1.17 Hz，两者接近时会发生共振现象，会造成使用安全问题和相应的舒适度问题，所以需要对该人行景观桥进行合适振动舒适度分析和相应减振控制分析。

（2）通过MIDAS有限元软件对人行景观桥结构进行动力时程分析，结果表明：作用频率为1.17 Hz的人群荷载激励后，该人行景观桥发生共振现象，其跨中竖向加速度峰值达到了51.64 cm/s2，超出了振动舒适度规范限值50 cm/s2，所以该结构需要进行相应的减振控制。

（3）该人行景观桥需在最长跨跨中区域共布置5个TMD-I，其频率为1.17 Hz，单个TMD质量1.2 t，减振系统总质量6.0 t。在作用人群荷载激励后，人行景观桥跨中竖向加速度得到了很好的控制，竖向加速度峰值均小于舒适度标准限值50 cm/s2，减振控制的结果满足振动舒适度评价标准。

以该人行景观桥为案例，针对类似工程振动问题，通过人致振动舒适度的分析后，合理布置TMD进行减振，被证明是一种有效的工程减振方法。

同时，实际结构的自振频率可能和设计时自振频率有一些出入，在安装TMD之前还需要进行楼板的振动实测，获得实际的自振频率。TMD产品参数需要具有一定的可调节余量，并能现场可调。