基于Hoek-Brown强度准则的浅埋隧道掌子面稳定性分析

张世民付开黄睿杨桦郭帅

（1.绍兴文理学院土木工程学院，绍兴 312000；2.浙大城市学院土木工程系，杭州 310015；3.浙江省岩石力学与地质灾害重点实验室，绍兴 312000；4.浙江省建设工程质量检验站有限公司，杭州 310012；5.浙江华蕴基础工程有限公司，湖州 313200）

0 引言

浅埋盾构隧道中，施加合理的支护力能够保证掌子面的稳定性，当掌子面前方施加的支护力不足或者过大时将引起掌子面发生破坏，支护力不足时将导致浅埋盾构隧道的主动破坏，支护力过大时将导致被动破坏。为此，浅埋隧道掌子面的稳定性已受到广泛的关注［1］。目前研究浅埋隧道掌子面稳定性的常用方法主要为室内模型试验、理论推导、数值模拟等。Leca等［2］构建了浅埋隧道掌子面的主动和被动破坏两种模式，基于极限分析理论研究了浅埋隧道掌子面的稳定性。Soubra［3］在Leca等［2］提出的破坏模式的基础上进行了改进，得到了浅埋隧道掌子面的三维破坏模式，获得掌子面稳定性的最优的上限解。李得建等［1］构建了倾斜地表条件下浅埋隧道掌子面的三维被动破坏模式，引入非线性强度准则研究了掌子面的稳定性。阳军生等［4］提出了自适应性有限元网格技术，构建浅埋隧道掌子面的破坏模式，进行了各种参数下有限元的计算，揭示了掌子面稳定性的精细化的破坏模式。

当岩土材料处于饱和状态时，岩土工程的稳定性受材料之间的孔隙水压力的影响显著［5］。Skempton［6］首次将孔隙水压力引入到极限分析中，基于有限元技术研究边坡的稳定性，研究表明孔隙水压力对边坡的稳定性影响显著。Huang等［7］基于极限分析理论，利用岩土材料的非线性Mohr-Coulomb强度准则，并考虑孔隙水压力的作用分析其对隧道塌落的影响。Yu等［8］在极限分析定理的框架内研究了考虑孔隙水压力作用下的深埋隧道拱顶塌落，结果发现孔隙水压力对隧道拱顶塌落有着显著的不利影响。

本文基于极限分析定理，考虑孔隙水压力的作用，构建出二维有限多块体的浅埋隧道掌子面的被动破坏模式，为研究其稳定性本文引入了经典的Hoek-Brown破坏准则。结合极限分析定理和虚功率原理得到了浅埋隧道掌子面被动破坏模式下的极限支护力的表达式，利用非线性规划函数解出其上限解。通过参数分析，研究了工作面稳定性的影响因素。

1 浅埋隧道被动破坏机制

1.1 基本假设条件

在浅埋隧道掌子面稳定性的分析中合理应用极限分析理论的前提是假设隧道周围岩土体应视作为服从相关联动法则的理想的刚性塑性体，可忽略其变形［9-11］。因此，本文方法的解析解是基于上述基本假设，主要针对软弱围岩提出，以完善目前对浅埋隧道掌子面的稳定性评价。

1.2 被动破坏模式构建

构建浅埋隧道掌子面的被动破坏模式见图1，该破坏模式由有限个平动的刚性多块体组成，P表示为隧道掌子面上作用的极限支护力，本文构建的浅埋盾构隧道掌子面的二维刚性有限多块体破坏机制见图1，h为隧道的开挖高度，H为浅埋隧道的埋深。

图1 浅埋隧道掌子面的被动破坏模式Fig.1 The passive failure mode of shallow tunnel face

1.3 破坏准则

本文采用Hoek-Brown破坏准则，该准则经过多年的不断发展，该准则已经经过多次的修正，最新的表达形式为［12-13］

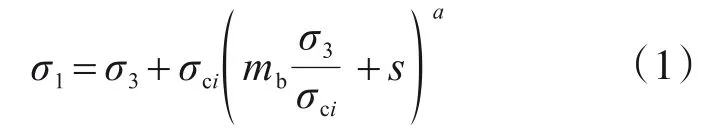
式中：σ1和σ3分别为岩土材料破坏时的最小和最大主应力；a、s和mb通过试验可获得［14-15］，具体计算见式（2）—式（4）。

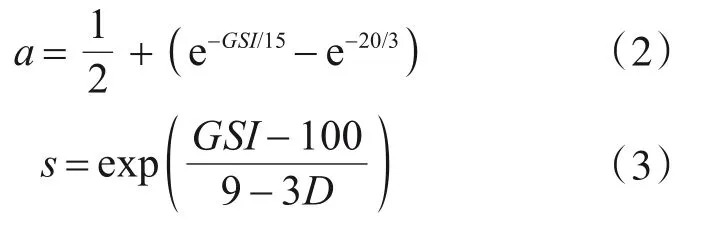
式中：D表示扰动因子；mi为试验中可获得的无量纲常数；GSI表示为地质强度指标。

经过等效Mohr-Coulomb强度准则中的内摩擦角和黏聚力可以用Hoek-Brown破坏准则的参数来表示：

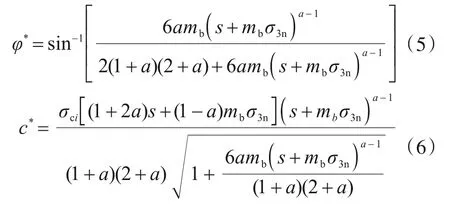
式中，σ3n表示室内三轴试验中的最大围压。

1.4 计算过程

浅埋隧道掌子面的被动破坏模式中的几何和速度关系见图2，在机动许可速度场中三角刚性体OC1C2的速度假定为v1，速度v1的数值不为0。根据破坏机制中各块体之间的几何关系和速度关系［14］如下。

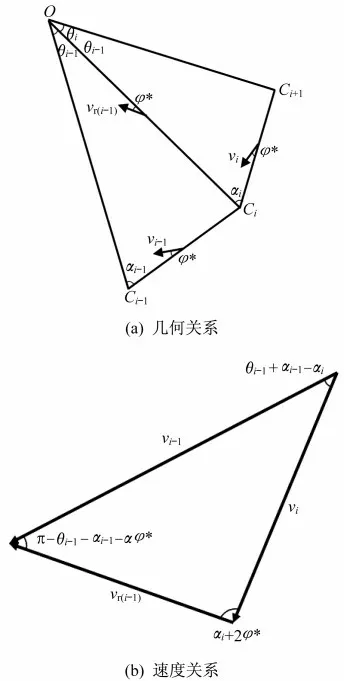
图2 几何、速度关系Fig.2 The geometric relationship and velocity relationship

1.4.1 速度关系

根据各个三角块体的速度组成的三角关系得到如下速度的关系：

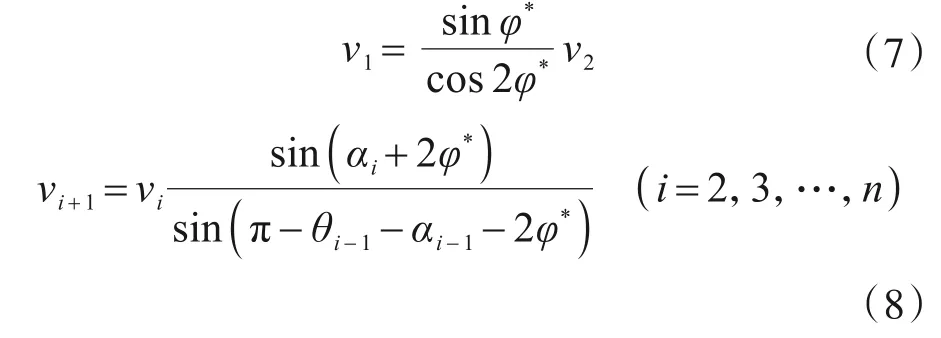
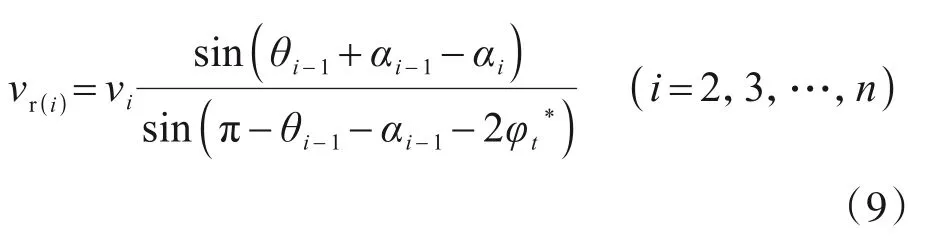
破坏模式中，刚性三角块体的速度的方向和垂直方向的夹角为βi：

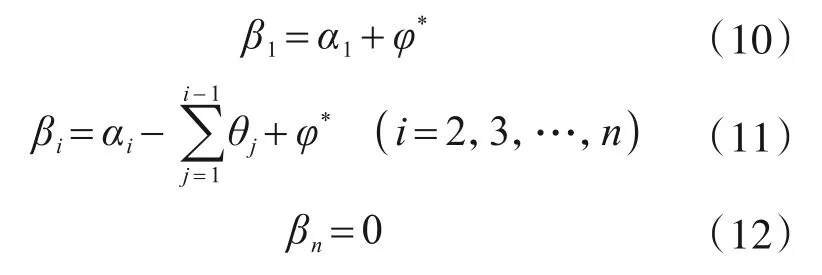
1.4.2 几何关系

图1所示的刚性块体的边长可根据三角形的正弦和余弦定理得到，表达式分别如下：

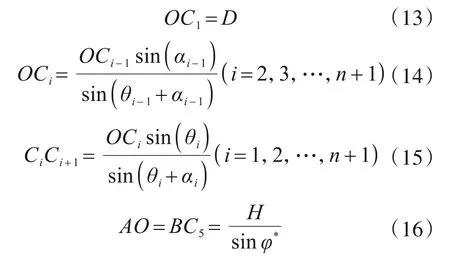
图1破坏机制中各个刚性块体的面积表达式分别为

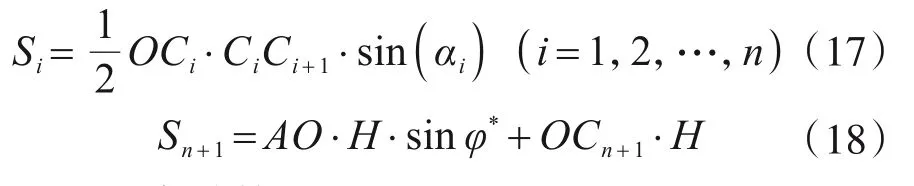
1.4.3 功率计算

利用极限分析定理，图1所示的浅埋隧道掌子面的被动破坏机制中的重力所做的功率可表达为

浅埋隧道掌子面的被动破坏机制中各速度间断线上产生的耗散能为

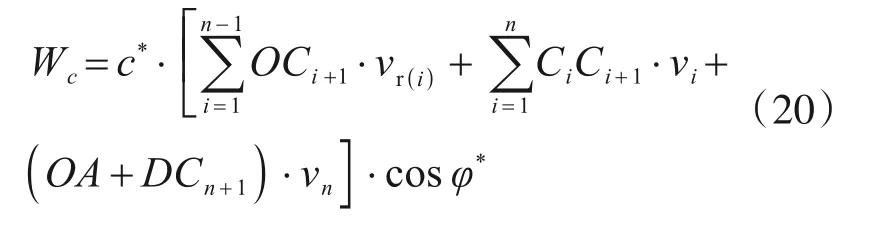
浅埋隧道掌子面上需要施加支护力，支护力在机动许可速度场中所做的功为

孔隙水压力为土壤或岩石中地下水的压力，可作为一种外力引入到极限分析定理中，在图1的破坏机制中，孔隙水压力在不同边界上做的功如下：

（1）首先在边界CiCi+1上所做的功可以表示为

（2）在破坏机制的上部边界OA上所做的功可以表示为

（3）同样地，在边界CBn+1上孔隙水压力所做的功可以表示为

根据上述讨论，孔隙水压力在机动许可速度场中做的总功是各边界上做的功之和，可以表示为

在虚功原理中，机动许可速度场中破坏机制内的内部耗散能总是和外力所做的功是相等的，即

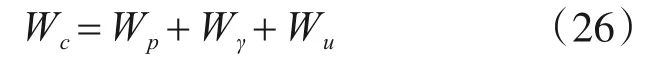
联合式（19）—式（26），可以推导得到浅埋隧道掌子面被动破坏模式下的极限支护力的表达式为

1.5 极限支护力优化求解

在极限分析定理的框架内，通过理论推导得到了浅埋隧道掌子面破坏机制下极限支护力的目标函数的表达式，利用多目标规划函数进行求解，求解之前需要确定目标函数的约束条件。

然后给出本文方法的计算流程图，如图3所示。

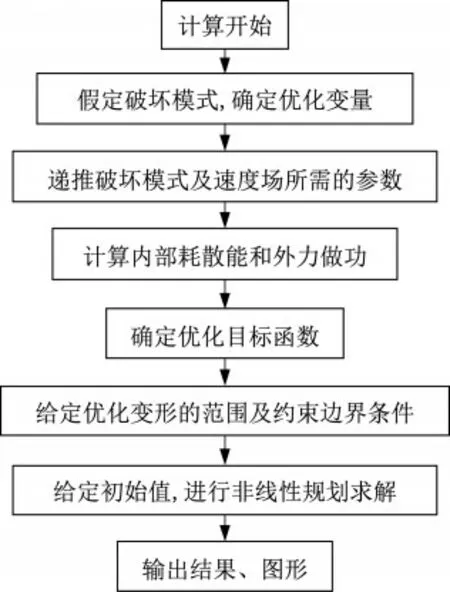
图3 计算流程图Fig.3 Flow chart of calculation

2 合理性验证

利用MATLAB软件进行多目标优化时，本文提出的机制中三角块体的数目取1～30，孔隙水压力系数取ru=0，隧道开挖高度h=10 m，重度γ=18 kN/m3，地质强度指标GSI=11.53，岩体单轴抗压强度σci=2.92 MPa，mi=25，扰动因子D=0。从图4可知，H/h=1，当块体数目不断增大到3时极限支护力达到了1 213 kPa，并且此后极限支护力基本保持不变，说明本文机制中块体数目为3时得到的极限支护力的数值精度已经满足需要［15］。

图4 极限支护力随三角块体数目变化图Fig.4 Change of ultimate support force with the number of triangular blocks

然后给定计算出不同的H/h下浅埋隧道掌子面的被动破坏机制下的极限支护力，参数如前所述，然后取不同的H/h（1、1.5、2及2.5）进行数值计算，将本文的解同参考文献［1］中的方法和数值模拟的解进行对比，如图5、图6所示，三种方法得到的极限支护力的解与H/h的变化趋势是一致的，即随着H/h的增大而增大，且最大误差为4.03%，说明本文求解浅埋隧道掌子面的被动机制下的极限支护力的方法是合理的。当然埋深对浅埋隧道掌子面的稳定性的影响还需要结合大量现场工程情况和试验进行深入的研究。

图5 结果比较Fig.5 Comparison of the results

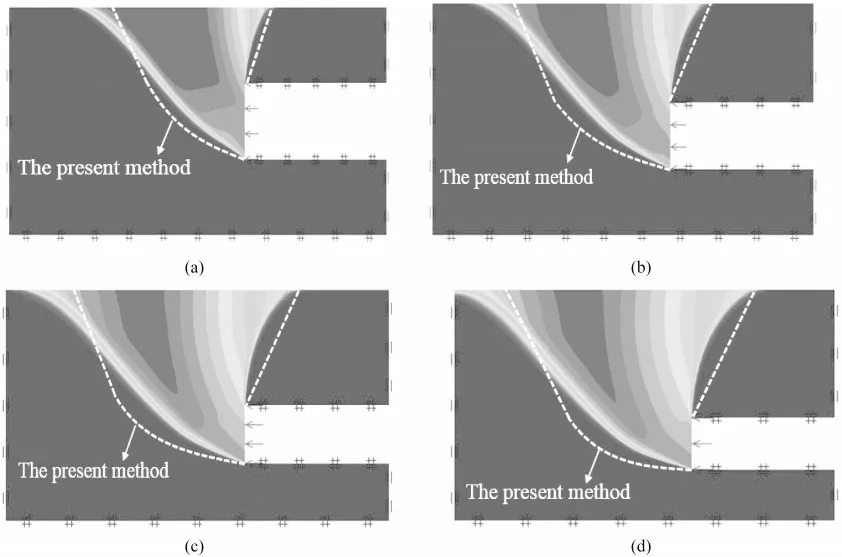
图6 本文方法和数值模拟得到的破坏范围对比Fig.6 Comparison of failure range obtained by this method and numerical simulation

3 参数影响分析

3.1 孔隙水压力系数

浅埋隧道埋深H和开挖高度h均取8 m，孔隙水压力系数ru=0～0.9，重度γ=18 kN/m-3，地质强度指标GSI=10，岩体单轴抗压强度σci=2.92 MPa，mi=25，扰动因子D=0，计算的块体数目取30。通过求解得到如图7（a）所示的不同孔隙水压力系数下的浅埋隧道掌子面的极限支护力，由图7（a）可知，随着孔隙水压力系数的增大，浅埋隧道掌子面的被动破坏机制下的极限支护力也不断增大。图8（a）表示的是不同孔隙水压力系数下浅埋隧道被动破坏的范围，孔隙水压力系数的增大将导致掌子面的被动破坏范围也增大，说明浅埋隧道被动破坏机制下掌子面的稳定性受孔隙水压力的影响明显。

3.2 地质强度指标

孔隙水压力系数ru取0～0.8，地质强度指标GSI取10、20及30，剩余参数同3.1节。根据图7（b）所示的计算结果，孔隙水压力系数取不同的数值时，浅埋隧道掌子面的被动破坏机制下的极限支护力随地质强度指标GSI的变化趋势相同，均随着地质强度指标GSI的增大而降低，这是由于被动破坏机制内的内部耗散能随地质强度指标GSI降低从而需要降低极限支护力，以减小外部力所做的功，虚功率原理得到满足［15］；不同地质强度指标GSI的浅埋隧道掌子面的被动破坏范围如图8（b）所示，当地质强度指标GSI不断增大时，浅埋隧道掌子面的被动破坏范围不断减小。

图7 掌子面的极限支护力参数影响分析Fig.7 Analysis of the influence of the parameters of the ultimate support force of the face

3.3 参数

孔隙水压力系数ru=0～0.8，无量纲参数mi=5～25，地质强度指标GSI=20，扰动因子D=0，其他参数同3.1节中内容。计算得到的极限支护力随着参数mi的变化趋势见图7（c），被动破坏机制的内部耗散能随着参数mi的增大而降低，从而导致极限支护力减小［15］；不同参数mi的浅埋隧道掌子面的被动破坏范围见图8（c），当参数mi增大时，浅埋掌子面的被动破坏范围不断减小。

3.4 扰动因子

孔隙水压力系数ru=0～0.8，地质强度指标GSI=15，扰动因子D=0～0.2，其他参数同3.1节中内容。在不同孔隙水下的极限支护力随着扰动因子D的变化趋势见图7（d）。当扰动因子D的增大时极限支护力也不断地增大；不同扰动因子D的浅埋隧道掌子面的被动破坏范围见图8（d），当扰动因子D增大时，浅埋隧道掌子面的被动破坏范围减小。

图8 掌子面的破坏范围参数影响分析Fig.8 Analysis of the influence of failure range parameters of the face

4 结论

（1）本文构建了浅埋隧道掌子面的二维平动有限多块体的被动破坏机制，基于极限分析定理并考虑孔隙水压力的作用，利用Hoek-Brown强度准则得到了浅埋隧道掌子面的被动破坏机制下的极限支护力的表达式，通过多目标规划求解可得到极限支护力的上限解。

（2）本文方法得到的浅埋隧道掌子面的被动破坏机制下的极限支护力的上限解和既有文献的解随着H/h的变化趋势一致，最大误差为4.03%，并且破坏范围基本一致，证明本文方法是合理的。

（3）通过对浅埋隧道掌子面的被动破坏机制下的极限支护力和破坏范围的参数影响进行分析，研究表明：随着孔隙水压力系数ru和扰动因子D的增大，浅埋隧道掌子面的被动破坏机制下的极限支护力和破坏范围均呈现出不断增大的趋势，而随着地质强度指标GSI和参数mi的增大呈现出不断减小的趋势；孔隙水压力对浅埋隧道掌子面的被动破坏机制下的极限支护力和破坏范围影响显著。

本文方法适用于处于软弱围岩的浅埋盾构隧道掌子面的稳定性分析，对于深埋隧道和传统矿山法施工隧道适用性还需要进一步研究。