复数在交流电路中的应用

王丹琦，任婷薇，李瑶，闫好奎

(1.新疆师范大学物理与电子工程学院电子系，新疆乌鲁木齐 830000；2.乌鲁木齐市第113中学，新疆乌鲁木齐 830000；3.新疆计量设计院，新疆乌鲁木齐830000)

目前，世界上电力系统所采用的交流电压，电流几乎都采用正弦函数形式，另一方面，其他各种复杂波形的电压电流，可以通过傅里叶级数也可分解为众多不同频率的正弦函数，所以，交流电路中大多数问题可以按照正弦电流电路来分析[1]。但是，在正弦交流电路中，常常遇到正弦量的加，减运算及微分，积分运算，如果直接采用三角函数公式来分析，将会非常复杂。如果用与正弦函数相对应的复数分析法进计算，可以将微积分方程简化为简单的代数方程，达到简化运算的目的[2]。

1 正弦交流电的表示方法

正弦交流电压，电流的大小和方向都是随时间发生变化的，其在任意时刻的值，称为瞬时值，表示为：

式中，Um(Im)、ω、φu（φi）是正弦量的三个要素。Um(Im)称为正弦电压u(电流i)的幅值，它是正弦量在整个振荡过程中所能达到的最大值，也是正弦量的极大值[3]。此处ω是称为角频率，它表示正弦量一秒中所转过的角度，单位是rad每s,它反映了相位随时间变化的角速度。我国电力系统的正弦电，其频率为50Hz，角频率ω为100π（rad/s）。φu（φi）是初相位，通常在主值范围内-π≤φu(φi)≤π取值。

在电路系统中，当电源频率是定值时，所有响应的频率都会和电源频率相同，只有响应的幅值和初相位会发生变化，所以在已知电源频率的条件下，确定一个正弦量只需求出幅值和初相位两个要素即可。

2 复数与正弦量的关系

2.1 复数的表示

我们把虚数单位-1记为j。一个复数A可用代数形式表示为：

式中，a1称为该复数的实部，记作a1=Re[A];a2称为该复数的虚部，记作a2=Im[A];Re和Im的含义为取复数的实部、取复数的虚部。

复数也可以表示为指数形式

式中，|A|为复数的模，恒为正，θ称为辐角，在-π≤θ≤π区间内取值[4]。

2.2 复数代数型和指数型的互换

（1）复数的指数型转换为代数型

可得：实部a1=|A |cosθ；虚部a2=|A |sinθ

（2）复数的代数型转换为复数型

已知A=a1+ja2，求| A|和θ？

根据复数三角形,可得：

（3）复数加减运算和乘除运算

复数的指数型转换为代数型只需用欧拉公式展开就可以，但是从代数型转换为指数型，位于不同象限的复数转换公式不同。两种表示方式的转换在求正弦交流电路分析时应用十分广泛,作乘除运算时，用指数型比较容易；做加减运算时，用代数型比较简单[5]。

2.3 用复数表示正弦量—相量法

可以发现，复数的指数表示形式也有两个要素，分别是模和辐角，与正弦量的瞬时值的幅值及初相位两个要素对应，且定义域也相同。如果用一个复数表示一个正弦量的两个要素，相当于给复数一个物理含义，此时的复数就被称为相量。

可见，相量也是复数，当一个复数的模表示一个电压的最大值，复数的辐角表示一个电压的初相位时，这个复数称为电压最大值相量；当一个复数的模表示一个电压的有效值，复数的辐角表示一个电压的初相位时，这个复数称为电压有效值相量；同理，相量也可以表示一个正弦电流瞬时值。

所有的相量都是复数，但不是所有的复数都是相量。只有复数的模和复数的辐角有一个确切的物理含义时，复数才被称为相量。当复数的模表示一个电压或者电流值的大小，复数的辐角表示一个电压或者电流的初相位时，这个复数才能被称为相量。即把代表正弦量的复数称为相量。为了区别相量和一般的复数，相量的写作方式就是在大写字母U或者I上面加“·”，既表示这一复数与正弦量关联的特殊关系，同时也区别于正弦量的有效值[6]。

相量是一个复常数，而正弦量是一个关于t的函数，所以二者并不相等；只能互相表示，且相量只能表示正弦量的幅值和初相位两个要素，而不能表示正弦量的角频率。正弦量和最大值相量的关系为：正弦量最大值相量与旋转相量e-jωt的乘积在X轴上的投影就是正弦量的瞬时值[7]。

3 电路三大定律的时域法和相量法分析

正弦稳态电路方程是一组同频正弦函数描述的代数方程，电路的基本定律所涉及的正弦电流，电压的运算，不会改变电压，电流同频正弦量的性质，即正弦量三大定律运算的结果，仍然是同频的正弦量[8]。

3.1 三大定律的时域形式

电路定律中的基尔霍夫电流定律和电压定律在交流电路中涉及三角函数的加减法，为使结果为同频率的正弦函数，还需应用到积化和差公式和余弦合角公式；欧姆定律除了有代数运算，还有微积分运算；三大定律的时域法给分析电路和计算都带来了困难。

3.2 三大定律的相量形式

相量法巧妙地将三角函数的运算和微积分运算都转换为代数运算。应用相量法分析正弦稳态电路时，其电路方程仍然为线性代数方程，只是电路变量的形式为三角函数形式，所以，电路的三大定律和电阻电路的各种分析方法都可以推广用于线性电路的正弦稳态分析[9]，差别仅在于所得电路方程为以相量形式表示的代数方程以及用相量形式表示的电路定理，而计算为复数计算。

4 复数分析交流电路

4.1 在加减运算中的应用

计算复杂，容易出错。相量法将三角函数复杂的运算过程转换为复数的代数运算，避免了烦琐的运算，提高了解题的速度[10]。

4.2 在微积分方程中的应用

例:如图所示电路，已知i=2 2cos5t(A),求电压u。

（1）时域法：

解：其中，如图1所示，各元件的电压分别为

图1 电路图

时域法过程为：

（2）相量法：

令未知电压相量为U˙。由于ω=5rad/s,根据各元件值可得：

于是可以画出电路的相量模型，如图2所示。由图2可计算各元件电压分别为：

图2 相量图

图3 时域法和相量法对比

如果用时域法进行电路分析，除了涉及微积分的运算外，对于电路中的加减运算，还需应用到积化和差公式和余弦合角公式，给分析电路和计算都带来了困难。相量法将微积分运算巧妙地转换为代数运算，并且对于正弦交流电路中的加，减运算也起到了简化作用[12][13]。相量法既简便又快捷直观准确。

4.3 用复数判断电路的性质

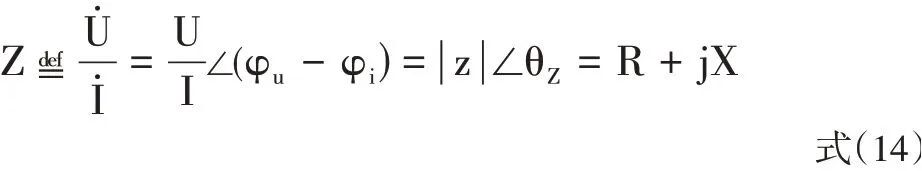
z表示电路中电压和电流的

有效值之比，辐角θZ表示同频电路电压和电流的相位差；Z的实部R表示电路中的电阻大小，Z的虚部X表示电路中电抗的大小。

通过Z可以判断电路的性质，分为两种情况：

当电路中电压和电流的初相位为已知时，可以通过求解Z的辐角θZ来判断[15]。当θZ=0°时，电压和电流同相，电路呈现阻性；当θZ＞0°时，电压超前电流，电路呈现感性；当θZ＜0°时，电压滞后电流，电路呈现容性。

表1 通过辐角θZ判断电路性质

通过Z的辐角θZ判断电路的性质时，主要取决于电路中的元件和元件的参数，与电路中元件之间相互连接方式没有直接关系。

当电路中电阻、容抗、感抗等参数为已知时，通过电路的连接方式，求出Z=R+jX，若X=0,则电路呈现阻性；若X＞0,则电路呈现感性；若X＜0，则电路呈现容性。

5 总结

用相量法表示正弦量只是数学形式变换，但是这种变换使得电路变量的求解步骤更加清晰，求解过程更加简单明了。对于方程的形式而言，从时域微积分方程转换成为简单的复数形式的代数方程，元器件的伏安关系也变为了简单的代数关系，更加容易理解和记忆。对于方程的求解过程而言，这些复数虽然只表示了正弦量的有效值和初相位这两个要素，但是因为响应和激励同频的性质，所以频率参数可以不参与电路方程运算，使得方程的计算得到了简化。