向斜作用下回采巷道冲击地压力学分析及冲击特性研究

张科学，朱俊傲，何满潮，亢 磊，姜耀东，李 东，孙健东，程志恒，王晓玲，杨海江，吴永伟，闫星辰，李举然，尹宇航

(1.华北科技学院 河北省矿山智能化开采技术重点实验室，北京 101601；2.中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，北京 100083；3.华北科技学院 智能化无人开采研究所，北京 101601； 4.中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室，北京 100083；5.煤炭科学研究总院，北京 100013；6.华北科技学院 矿山安全学院，北京 101601)

0 引 言

向斜构造在地壳中分布十分广泛，在煤系地层中比较常见，是岩层在构造作用下形成的一系列连续弯曲。相关研究[1-4]及实践证明[3，5-9]向斜构造是影响冲击地压发生的重要因素之一，义马矿区、大同矿区、京西矿区等冲击地压案例表明，在次一级的向斜构造轴部，倾角大于45°的翼部及其转折部位是冲击地压的多发区域。国内外相关学者从构造应力场的角度对向斜作用下冲击地压的发生规律和特征进行了研究。康红普等[10]通过地应力实际测量，建立了相应的向斜数值模型，研究了甘肃华亭矿区的大型向斜构造，得到了向斜轴部水平应力明显大于垂直应力，且向斜轴部水平应力也明显比向斜翼部水平应力大。宋佩德等[11]建立了不同构造应力条件下工作面冲击地压计算模型，研究了构造应力对煤层及其顶底板围岩应力场和能量场的影响，得到了高水平构造应力场是试验矿井冲击地压发生的主要影响因素。陈国祥等[12]建立了褶皱区不同介质接触型冲击地压突变模型，研究认为向斜附近区域煤岩体更容易积聚能量，而其积聚的能量在开采扰动下易引发冲击地压，使该区域冲击地压危险程度更高。陈国祥等[13]还开展了褶皱区应力场对冲击地压影响的相关研究，认为工作面自背斜轴部开采时，支承应力集中系数比自向斜轴部开采大，工作面从褶皱翼部开始回采冲击危险程度更小；当褶皱背向斜同时存在时，工作面从褶皱背斜轴部开始俯采时，冲击危险性远高于从褶皱向斜轴部开始仰采的危险性。王存文等[14]根据褶皱的纵弯形成机制，将褶皱分为5个区，不同部位具有不同的应力状态，研究认为向斜轴部区域水平应力集中较大。王宏伟等[15]通过相似模拟试验分析了开采扰动条件下断层滑动面切应力的动态演化特征，得到了工作面回采过程中断层面上声发射事件数的分布规律，构建了断层赋存条件下的工作面回采模型，得到了断层滑移失稳时切应力分布和能量释放的动态演化特征，总结了断层滑移失稳的前兆信息。王桂峰等[16]把巷道围岩作为一个整体进行冲击地压空间孕育机制的研究，提出“一大两小”的孕育模型，研究表明向斜构造引起的应力场是冲击矿压发生的内在应力根源，并通过采用顶板岩层深孔爆破的措施进行防治。然而，相关学者多是从向斜构造应力场[17-20]及周围大采场环境下进行研究与评价[21-24]，且多是从宏观进行探讨其发生规律及孕育机理，虽然回采巷道冲击地压在冲击事故中占多数[25]，但并没有引起学者们的足够重视，尤其对向斜作用下回采巷道冲击地压的深入研究更是少见。因此通过力学分析、数值计算及现场实践相结合的方法，深入研究向斜作用下回采巷道围岩冲击特性，以希望取得一些有益结论，对同类型地质条件下回采巷道冲击地压预防与治理具有借鉴意义。

1 工程概况

试验巷道为某矿区21221工作面运输巷(以下简称“下巷”)，该矿井设计生产能力为60万t/a，2007年核定生产能力为210万t/a；主采2号煤层，煤层倾角为3°～13°，平均倾角为10°；煤层平均厚度为10 m；煤层普氏系数为1.5～3.0，煤层节理、层理发育；煤层直接顶为0～24 m的脆性泥岩，基本顶为侏罗系巨厚砾岩，且厚度为179～429 m，平均410 m。21采区采掘工程平面如图1所示。

2 向斜作用下回采巷道力学分析

2.1 回采巷道应力集中分析

将煤矿巷道围岩的应力求解简化为弹性力学中的求解矩形孔口区域的应力问题[26]，如图2a所示，带小圆孔的矩形板，受x向均布拉力q1，y向均布拉力q2，可以将荷载分解为2部分：第1部分是四边的均布拉力，如图2b所示，得到应力解答：

(1)

式中：σρ为圆形巷道沿ρ方向的径向正应力；σφ为圆形巷道沿φ方向的切向正应力；τρφ、τφρ均为圆形巷道切应力；r为圆形巷道半径；ρ为极坐标系中的极径；φ为极坐标系中的极角；q1为x向均布拉力；q2为y向均布拉力。

第2部分是左右两边的均布拉力和上下两边的均布压力，如图2c所示，得到应力解答：

(2)

将式(1)和式(2)解答叠加，即得原荷载作用下的应力分量：

(3)

由于原岩应力场是分析开采空间周围应力重新分布的基础，研究岩体的初始应力状态，为分析开挖煤岩体过程中煤岩体内部应力变化[27]、合理设计巷道支护提供依据。原岩应力场主要由自重应力场和构造应力场组成。

2.2 向斜作用下回采巷道力学分析

2.2.1 向斜作用下回采巷道力学模型

地壳自然运动过程中，大规模或者区域岩石受力弯曲变形形成向斜构造，因此在向斜构造的受力分析时，可以通过岩石的弯曲变形进行简化处理，而弯曲弹性梁的应力应变关系可以很好地描述岩石弯曲变形的过程。岩层在弯矩M的作用下弯曲，以中性层为界，下部受拉应力作用，上部受压应力作用，并且拉(或压)应力离中性层越远越大，其最大值在远离中性层最远的上下边缘处，如图3所示。

在岩层本身弯曲(纯弯曲)所决定的应力状态中，最大和最小压应力(σ1和σ2)垂直或者平行于岩层表面(与位于中性层上、下有关)，并垂直于向斜轴，而中间应力平行于岩层面和向斜轴[28]。

因此，岩层的最大拉应力为：

(4)

式中：σ1为最大拉应力；y为应力点距中性层的距离；E为巷道围岩弹性模量；ρ′为向斜构造曲率半径。

若令q1=σ1，q2=-γH(γ为覆岩容重，H为埋深)，代入式(3)，解出向斜作用下回采巷道围岩应力分布：

(5)

2.2.2 向斜作用下回采巷道力学分析

该矿区向斜构造走向一般为东西方向，向斜翼间角约为160°；煤层平均埋深为758.5 m；21221工作面长度约为176 m，下巷巷道半径近似为3.0 m。

(6)

综上所述可知：向斜作用下回采巷道底板围岩应力集中较大，应力集中系数为5.8，且为拉应力，易发底板冲击；帮部围岩应力集中相对较高，应力集中系数为3.6，为压应力，可发生帮部冲击；顶板围岩应力较小，不易发生顶板冲击。

3 向斜作用下回采巷道冲击特性

3.1 CDEM数值软件介绍及模型建立

3.1.1 CDEM数值软件介绍

连续-非连续单元方法(CDEM)是中国科学院力学研究所非连续介质力学及工程灾害联合实验室提出的适用于模拟材料在静、动载荷作用下非连续变形及渐进破坏的一种数值算法。CDEM具有将有限元与离散元耦合计算、单元体破裂、大变形位移、GPU加速等优点[3]。因此，基于CDEM数值软件的优点，对采矿工程中的大变形、垮落、断层位移场等问题，更具有真实直观性和实际参考价值。

3.1.2 数值模型建立

数值模拟工程背景以该矿21221工作面下巷为数据支撑，并结合矿区向斜、力学分析及相关文献进行统筹，将向斜作用下回采巷道围岩冲击特性数值模拟方案分为2个，分别为向斜轴部回采巷道冲击地压模型和向斜翼部回采巷道冲击地压模型。数值模型建立采用CDEM数值软件，依据现场数据确定数值模拟中向斜翼间角(正交剖面上两翼间的内夹角，圆弧形向斜的翼间角是指通过两翼上2个拐点的切线之间的夹角)为160°，为平缓向斜。

CDEM数值模型建模思路及过程具体如下[3]：①在AutoCAD中建立向斜作用下回采巷道冲击地压模型；②AutoCAD模型文件以DXF格式输出保存；③把 .dxf文件导入GID软件，并在GID软件中进行分组及复杂网格划分操作；④把GID模型以ASCII文件格式(美国信息交换标准代码)输出，最后以 .msh文件保存；⑤把 .msh文件导入CDEM数值软件，模型建立完成。

模型边界条件主要是根据工作面的现场地质条件和向斜地质特征，并综合考虑各方面的因素确定的。模型的边界条件为左右边界水平方向固定，底边界垂直方向固定，顶部自由边界。依据现场地应力测试结果对模型开挖前应力场进行设置，最大水平主应力约为22.87 MPa，最小水平主应力约为11.67 MPa，垂直主应力约为19.54 MPa。

向斜作用下回采巷道冲击地压数值模型，如图6所示。整个模型尺寸(长×高)确定为：266 m×247 m，+X方向为工作面的推进方向，+Y方向为垂直向上。模型巷道尺寸(长×高)确定为：6 m×5 m。

图6 向斜作用下回采巷道冲击地压数值模型Fig.6 Numerical model of mining roadway under influence of syncline

3.1.3 岩体力学参数

数值模型中材料本构模型为摩尔-库仑模型，模拟中各煤岩层的岩体力学参数参考了煤岩块力学性能测试结果以及当地地质资料等，最终得到各岩层的岩体力学参数，见表1。

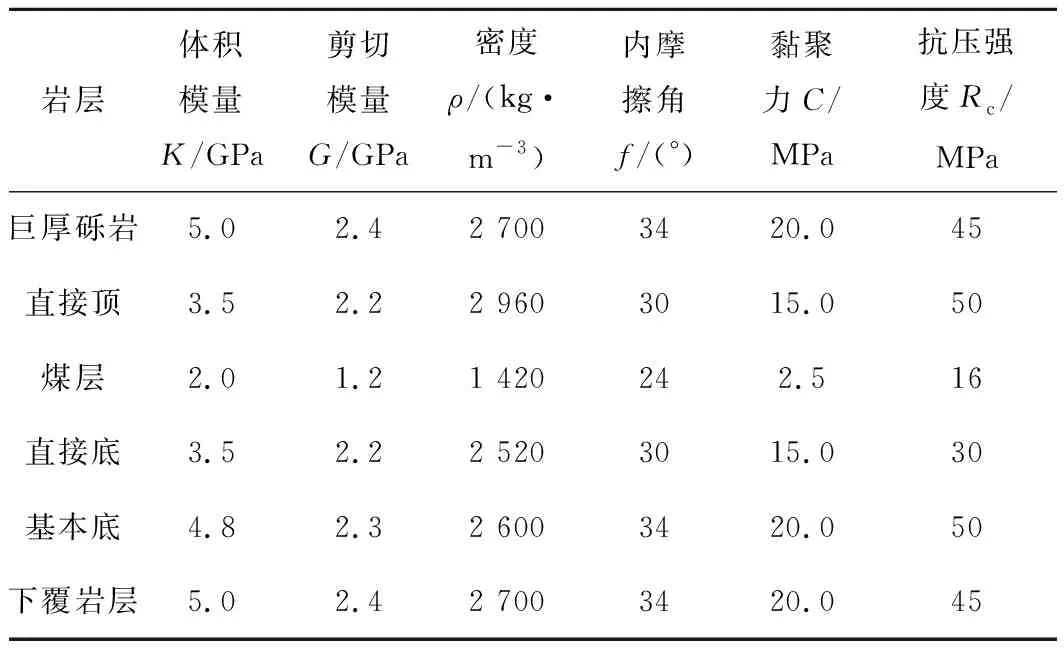
表1 数值计算模型的岩体力学参数

3.2 向斜轴部回采巷道围岩冲击特性分析

巷道冲击地压的本质原因是巷道围岩在高应力作用下的突然失稳、变形和破坏。巷道围岩冲击特性主要是指巷道冲击地压在孕育、发生过程中伴随着周围煤岩体应力场转移、能量场积聚、塑性区扩展和位移场演化(三场一区)，巷道围岩的应力场、能量场、塑性区和位移场是巷道围岩冲击特性的表现形式。

重点关注巷道顶板围岩、底板围岩和两帮围岩，

并分别在巷道的四周布置监测点，分别监测巷道顶板、底板、左帮、右帮和底板深部围岩的应力、能量和位移变化情况[29-30]，巷道顶板、底板、左帮和右帮表面围岩监测点序号分别为1、2、3和4，巷道底板深部围岩监测点序号分别为21、22、23、25和28(以28监测点序号为例，代表意义：前面数字2为底板，后面数字8为底板表面距监测点深度为8 m)，巷道围岩监测点布置序号及深度如图7所示。

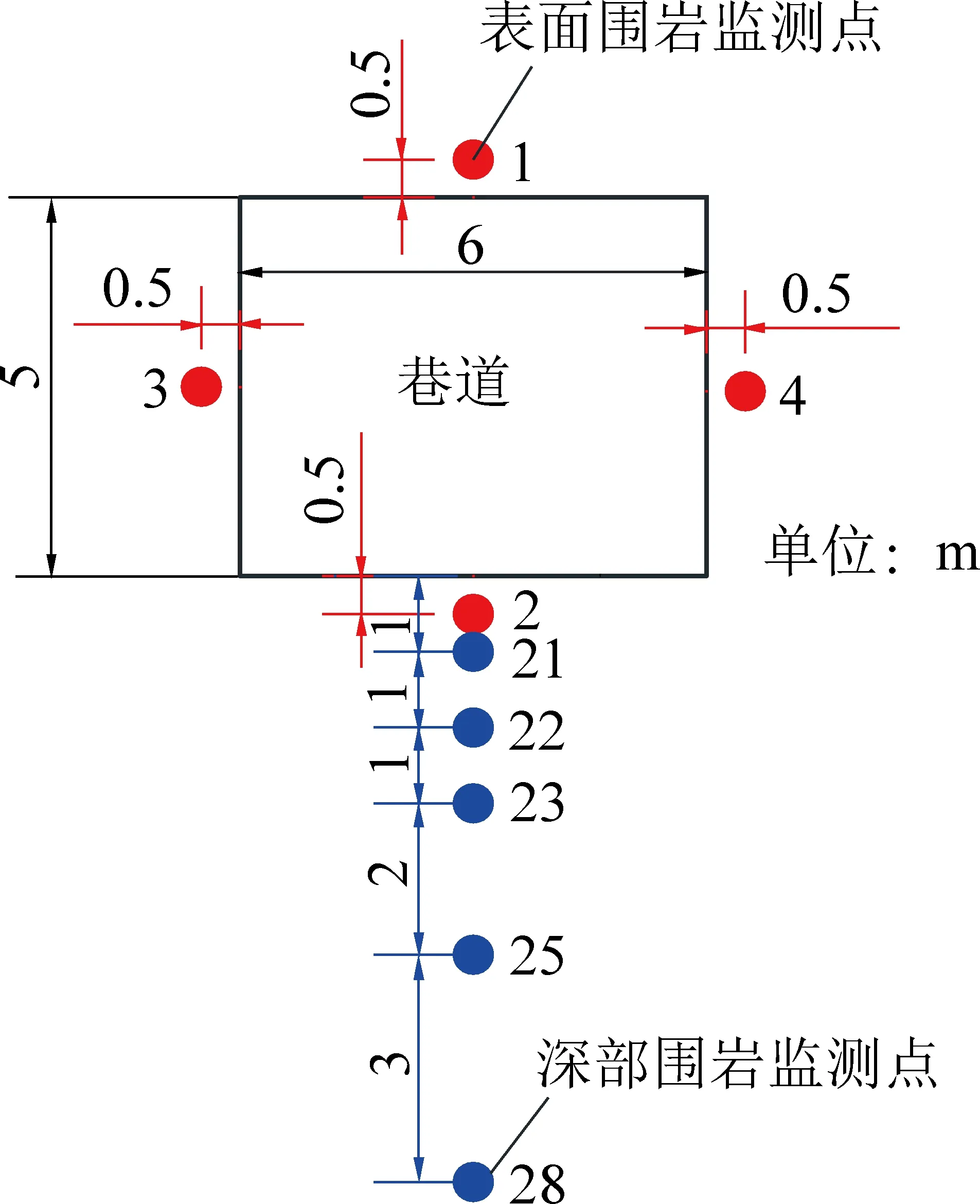
图7 巷道围岩监测点布置序号及深度Fig.7 Arrangement of surrounding rock monitoring points

3.2.1 应力场演化规律

统计和分析CDEM数值软件计算结果，发现向斜轴部采场及巷道围岩水平应力场演化规律，如图8所示。向斜轴部巷道围岩应力演化特征，如图9所示。

图8 向斜轴部采场及巷道围岩水平应力场Fig.8 Working face and roadway surrounding rock near synclinal axis

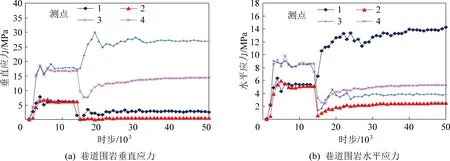
图9 向斜轴部巷道围岩应力演化特征Fig.9 Stress evolution of roadway surrounding rock near synclinal axis

由图8和图9分析可知，采动影响下向斜轴部回采巷道围岩应力场演化特征及规律如下：

1)向斜轴部回采巷道围岩应力随采动影响总体上呈现先急剧增大，后持续稳定，然后突变降低，最后持续稳定在高应力状态或低应力状态；巷道围岩垂直应力最后稳定值高于水平应力。

2)巷道表面围岩应力中底板应力最小，两帮的垂直应力和水平应力明显高于顶底板，且帮部的垂直应力可以保持相对的高应力状态；左帮的垂直应力和顶板的水平应力发生复杂变化后稳定在一种相对高应力状态，其最后的稳定应力分别为26.9 MPa和17.2 MPa；巷道表面围岩垂直应力平均值为11.5 MPa，水平应力平均值为6.2 MPa。

3)采动影响下向斜轴部回采巷道底板深部围岩应力总体上呈现先急剧增大，后小范围下降，再持续稳定波动，然后突变降低，最后缓慢稳定；底板深部围岩应力呈现相同的规律性变化，底板1～3 m围岩最后的稳定应力约为其峰值应力的1/4，甚至更低；底板5～8 m围岩最后的稳定应力约为其峰值应力的1/3～1/2。

3.2.2 能量场演化规律

计算结果发现，向斜轴部回采巷道围岩能量场变化具有一定的规律性，其围岩能量演化特征，如图10所示。

图10 向斜轴部巷道围岩能量演化特征Fig.10 Energy evolution of roadway surrounding rock near synclinal axis

由图10分析可知，采动影响下向斜轴部回采巷道围岩能量演化特征如下：

1)采动影响下向斜轴部回采巷道围岩能量总体上呈现先急剧增大，后持续稳定，然后突变降低，最后持续稳增加到一定应力状态，或者稳定不变；对比分析向斜轴部巷道围岩应力可知，巷道围岩应力和巷道围岩积聚的能量存在着某种的对应关系。

2)巷道表面围岩积聚的能量中底板最小，最后其能量值为0；两帮围岩积聚的能量整体上高于顶底板围岩，顶板和两帮围岩最后积聚的能量值稳定在一定水平，其中顶板围岩积聚的能量最后稳定在76.3 kJ/m3。

3)采动影响下向斜轴部回采巷道底板深部围岩能量总体上呈现先急剧增大，后小范围下降，再持续稳定波动，然后突变降低，最后缓慢稳定在一定水平上；底板深部围岩能量整体上释放的较多，其中底板0～3 m围岩释放能量的程度大于底板深部5～8 m。

3.2.3 位移场演化规律

向斜轴部采场及巷道围岩位移场演化规律，如图11所示。向斜轴部巷道围岩位移和移近速度演化特征，如图12所示。

图11 向斜轴部采场及巷道围岩位移Fig.11 Displacement of working face and roadway near synclinal axis

d—位移； v—速度；下角1，2，3，…，28—测点；下角x,y—方向

由图11和图12分析可知，采动影响下向斜轴部回采巷道围岩应力场演化特征及规律如下：

1)采动影响下向斜轴部回采巷道围岩变形以顶底板变形为主，两帮变形为辅，底鼓尤为突出。

2)在第13 000时步巷道围岩开始出现急剧变形，其中底板的移近速率最高，最大值达到2.8 mm/step，在20 000时步巷道围岩变形基本处于稳定状态，但其巷道底鼓量已达1.0 m。

3)采动影响下向斜轴部回采巷道底板深部围岩变形呈现出先急剧升高，后持续稳定的状态；底板深1、2、3、5、8 m围岩的最大变形量分别为0.98、0.78、0.62、0.36和0.08 m，最大变形速率分别为2.79、2.76、2.71、2.22、1.74 mm/step，由此分析可知，底板1～3 m深度围岩变形较大，且变形剧烈；底板5～8 m深度围岩变形较小，较为稳定。

3.3 向斜翼部回采巷道围岩冲击特性分析

3.3.1应力场演化规律

向斜翼部采场及巷道围岩应力场演化规律和演化特征分别如图13和图14所示。

由图13和图14分析可知，采动影响下向斜翼部回采巷道围岩应力场演化特征及规律如下：

图13 向斜翼部采场及巷道围岩应力场演化规律Fig.13 Stress field evolution of working face and roadway near synclinal limb

图14 向斜翼部巷道围岩应力演化特征Fig.14 Stress field evolution of roadway near synclinal limb

1)采动影响下向斜翼部回采巷道围岩应力总体上呈现先急剧增大，后持续稳定，然后突变降低，最后持续稳定在高应力状态或低应力状态；巷道围岩垂直应力最后稳定值高于水平应力；向斜翼部巷道围岩在高应力状态下会发生应力转移、能量积聚，当其巷道围岩应力达到煤岩体强度极限时，煤岩体产生破坏，除煤岩体中保存的部分残余变形能外，其储存的应力(能量)将大部分或者全部释放，巷道围岩一部分应力向煤岩体深部转移，另一部分应力必定全部释放出来，因此会出现应力的突变降低。

2)巷道表面围岩应力中底板应力最小，两帮的垂直应力和水平应力明显高于顶底板，且帮部的垂直应力可以保持相对的高应力状态；左帮的垂直应力和顶板的水平应力发生复杂变化后稳定在一种相对高应力状态，其最后的稳定应力分别为31.2 MPa和8.5 MPa，其中顶板围岩水平应力明显低于向斜轴部巷道顶板围岩水平应力；巷道表面围岩垂直应力平均值为11.1 MPa，水平应力平均值为5.5 MPa。

3)采动影响下向斜翼部回采巷道底板深部围岩应力总体上呈现先急剧增大，后小范围下降，再持续稳定波动，然后突变降低，最后缓慢稳定；底板深部围岩应力呈现相同的规律性变化，且随底板深度的增加垂直应力稳定值更具有线性关系；底板深1 m围岩水平应力明显低于底板深度2～8 m处，其应力约为底板深5～8 m围岩应力的2/3。

3.3.2 能量场演化规律

向斜翼部回采巷道围岩能量场变化具有一定的规律性，其能量演化特征，如图15所示。

图15 向斜翼部巷道围岩能量演化特征Fig.15 Energy field evolution of roadway near synclinal limb

由图15分析可知，采动影响下向斜翼部回采巷道围岩能量演化特征如下：

1)采动影响下向斜翼部回采巷道围岩能量总体上呈现先急剧增大，后持续稳定，然后突变降低，最后持续稳增加到一定应力状态，或者稳定不变；对比分析向斜翼部巷道围岩应力可知，巷道围岩应力和巷道围岩积聚的能量存在着某种的对应关系。

2)巷道表面围岩积聚的能量中底板最小，最后其能量值为0；两帮围岩积聚的能量整体上高于顶底板围岩，顶板和两帮围岩最后积聚的能量值稳定在一定水平，其中左帮围岩积聚的能量最后稳定在103.4 kJ/m3。

3)采动影响下向斜翼部回采巷道底板深部围岩能量总体上呈现先急剧增大，后小范围下降，再持续稳定波动，然后突变降低，最后缓慢稳定在一定水平上；底板深部围岩能量整体上释放的较多，其中底板1 m深度围岩能量值仅为0.9 kJ/m3明显低于底板深度2～8 m围岩能量值，说明底板1 m深度围岩能量释放较多，巷道围岩变形破坏严重。

3.3.3 位移场演化规律

向斜翼部采场及巷道围岩位移场演化规律，如图16所示。向斜翼部巷道围岩位移和移近速度演化特征，如图17所示。

由图16和图17分析可知，采动影响下向斜翼部回采巷道围岩应力场演化特征及规律如下：

图16 向斜翼部采场及巷道围岩位移场变化规律Fig.16 Displacement field evolution of working face and roadway near synclinal limb

1)采动影响下向斜翼部回采巷道围岩变形中底板和帮部变形都较为严重；向斜翼部巷道围岩受向斜轴部构造应力影响，但是其影响程度较轴部小，也因此表现出向斜翼部巷道帮部变形也较为严重；巷道围岩垂直应力和水平应力的共同释放是底板和帮部变形破坏的根本原因，但水平应力的整体释放程度高于垂直应力，因此巷道围岩稳定后整体水平应力低于垂直应力。

2)在第15 000时步巷道围岩开始出现急剧变形，其中底板和右帮的移近速率较高，分别为1.7、1.68 mm/step，在23 000时步巷道围岩变形基本处于稳定状态，底板和右帮的围岩变形量分别为0.47、0.43 m。

3)采动影响下向斜轴部回采巷道底板深部围岩变形整体上呈现出先急剧升高，后持续稳定的状态；底板深度1、2、3、5、8 m围岩的最大变形量分别为0.39、0.29、0.24、0.16、0.06 m，最大变形速率分别为1.72、1.64、1.48、1.01、0.79 mm/step，由此分析可知，底板1 m深度围岩变形明显大于底板2～8 m深度围岩，且底板2～8 m深度围岩变形具有线性变化规律。

3.4 向斜轴部和翼部回采巷道围岩冲击特性对比分析

综上分析可知，向斜轴部与翼部巷道围岩冲击特性中表现出不同的规律，对比分析向斜轴部和翼部回采巷道(X轴为推进时步；Y轴为至向斜轴部距离，向斜轴部巷道为0 m，向斜翼部巷道为30 m；Z轴为应力、能量或位移)围岩应力场、能量场和位移场的数据呈现出一定的规律性，如图18所示。

d—位移； v—速度；下角1，2，3，…，28—测点；下角x,y—方向

由3.2节、3.3节和图18分析可知，采动影响向斜作用下回采巷道围岩冲击特性具有如下规律：

1)采动影响向斜作用下回采巷道围岩应力总体上呈现先急剧增大，后持续稳定，然后突变降低，最后持续稳定在高应力状态或低应力状态；巷道围岩垂直应力最后稳定值高于水平应力。

2)巷道围岩能量总体上呈现先急剧增大，后持续稳定，然后突变降低，最后持续稳增加到一定应力状态，或者稳定不变；巷道围岩应力和巷道围岩积聚的能量存在着正相关的对应关系。

3)向斜轴部巷道围岩变形以底鼓为主，向斜翼部巷道围岩变形是底板和帮部同时变形；向斜轴部巷道围岩变形整体上大于向斜翼部，其中向斜轴部巷道底鼓量约为向斜翼部的2倍；向斜轴部巷道底板深度1～3 m围岩变形剧烈，底板深度5～8 m围岩较为稳定，而向斜翼部巷道底板深度1 m围岩变形明显大于底板深度2～8 m围岩，且底板深度2～8 m围岩变形具有线性变化规律。

4 现场应用情况

21221工作面掘进期间共发生了3次巷道冲击地压事故。“8.16”矿震事件发生在距巷口约477 m，底鼓变形量约260 mm，造成单体柱向上帮歪斜，输送带架偏移。“8.31”矿震事件发生在距巷口约570 m，底鼓变形量约300 mm，造成下帮梁腿轻微滑移。“11·3”矿震事件发生在距巷口约550 m，底鼓变形量约350 mm，造成上帮移出210 mm，煤尘大，持续时间较长，冲击波大。冲击引起的回采巷道变形破坏以底鼓为主，并伴随上帮移出，下帮肩角鼓出等破坏。

根据21221工作面运输巷作业规程相关资料及现场实际，得知21221工作面现有支护体系主要有一级支护和二级支护，即锚杆支护体系和联合支护体系(36U型钢+锚杆支护体系)。现有支护体系在发生冲击时不能有效地控制巷道变形，使巷道围岩变形严重，尤其是巷道底鼓没有得到很好控制，严重威胁矿井安全生产。根据21221工作面运输巷冲击地压发生影响因素及围岩变形特点，提出了采用锚杆支护体系+“O”型棚+门式液压支架(或垛式液压支架)的强力柔性支护体系，为回采巷道冲击地压综合支护体系中的三级支护，此强力柔性支护体系在该矿的回采巷道防冲支护中得到了良好的应用。21221工作面巷道强力柔性支护断面参数设计如图19所示。

图19 21221工作面巷道强力柔性支护断面参数设计Fig.19 Parameter design drawing of strong flexible support section of No.21221 working face roadway

综合21221工作面下巷微震、电磁辐射、钻孔应力和巷道围岩变形监测规律可以得出回采巷道冲击地压前兆规律如下：

冲击事件发生前3～5 d微震能量和频次信号均出现上升趋势，之后1～4 d达到峰值后下降，在下降后2～3 d发生冲击事件；电磁辐射强度在冲击事件发生之前1～2 d出现高值，且整体上在冲击前后呈现“∧”型和“N”型变化趋势；钻孔应力在冲击发生前7～28 d出现连续上升趋势，冲击发生前1～2 d达到峰值，之后开始下降，在下降过程中发生冲击；冲击事件发生前15～20 d顶底板移近量出现连续增大的趋势，冲击发生前1～2 d达到峰值后突然下降，在下降过程中发生冲击。

强力柔性防冲支护体系在回采巷道冲击地压现场应用效果较好，防冲支护体系在控制巷道围岩变形中起到了关键控制作用，且冲击地压发生后，巷道仍可以满足矿井安全生产。

5 结 论

1)向斜作用下回采巷道底板围岩应力集中较大，易发底板冲击；帮部围岩应力集中相对较高，可发生帮部冲击；顶板围岩应力较小，不易发生顶板冲击。

2)向斜作用下回采巷道围岩能量随采动影响总体上呈现先急剧增大，后持续稳定，然后突变降低，最后持续稳增加到一定应力状态，或者稳定不变；巷道围岩应力和巷道围岩积聚的能量存在着正相关的对应关系。

3)向斜轴部巷道围岩变形以底鼓为主，向斜翼部巷道围岩变形是底板和帮部同时变形；向斜轴部巷道围岩变形整体上大于向斜翼部，其中向斜轴部巷道底鼓量约为向斜翼部的2倍。

4)向斜轴部巷道底板深度1～3 m围岩变形剧烈，底板深度5～8 m围岩较为稳定，而向斜翼部巷道底板深度1 m围岩变形明显大于底板深度2～8 m围岩，且底板深度2～8 m围岩变形具有线性变化规律。