基于改进K-means和CNN的储罐罐底点蚀诊断模型*

王新颖，胡磊磊，刘 岚，徐 拓，林振源，黄旭安

(常州大学 环境与安全工程学院，江苏 常州 213164 )

0 引言

在储罐罐底腐蚀中，点蚀破坏性最大，是科研人员监测和研究的重点[1]。声发射由于其非破坏性技术(NDT)，被广泛用于管道泄漏[2]、疲劳断裂[3]、损伤检测[4]、腐蚀破坏和表面摩擦等检测。运用声发射技术分析因点蚀产生的缺陷及损伤信息，构建声发射源诊断模型，是目前相关领域研究的关键[5]。

随罐底腐蚀声发射研究的不断深入，卷积神经网络(CNN)能够解决传统BP神经网络收敛速度慢且易陷入局部极值的问题[6]。通过采用误差梯度进行训练，在一定程度上提高模型训练效率，减小“过拟合”风险[7-8]。实际应用中点蚀声发射源类别标签难以获取，而K均值聚类算法(K-means)无需标签数据，但无法事先确定合适的聚类数目，聚类质量不高[9-10]。

良好聚类效果获取的关键在于确定最佳的聚类数目，因此，本文在基于K-means引入肘部法则的思想，以确定最佳k值，并结合基于TensorFlow的CNN，建立储罐底板点蚀过程诊断模型。

1 储罐底板点蚀实验

1.1 实验材料

准备100 mm×250 mm×10 mm的Q235钢试样，实验开始前，用砂纸将钢试样表面打磨光滑，用酒精棉擦拭表面并放入干燥箱内备用，腐蚀溶液选用质量分数3.0%NaCl、pH=2.0的酸性溶液，检测仪器采用美国进口的micro-Ⅱ 2代声发射仪。

1.2 实验过程

储罐底板模拟点蚀试样如图1所示，选取试样中间部位，用打孔机打孔，表面形成凹槽，向孔中滴入配置好的腐蚀溶液，在孔周围涂满凡士林，防止边缘处产生缝隙。

图1 储罐底板模拟点蚀试样Fig.1 Simulated pitting corrosion specimen of tank bottom plate

实验装置如图2所示。整个实验在室内常温中进行，传感器涂满凡士林与试样表面紧密贴合，同轴电缆与通道连接，实时传送腐蚀信号，为减少外界振动干扰，试样底部与实验台之间衬有橡胶垫。

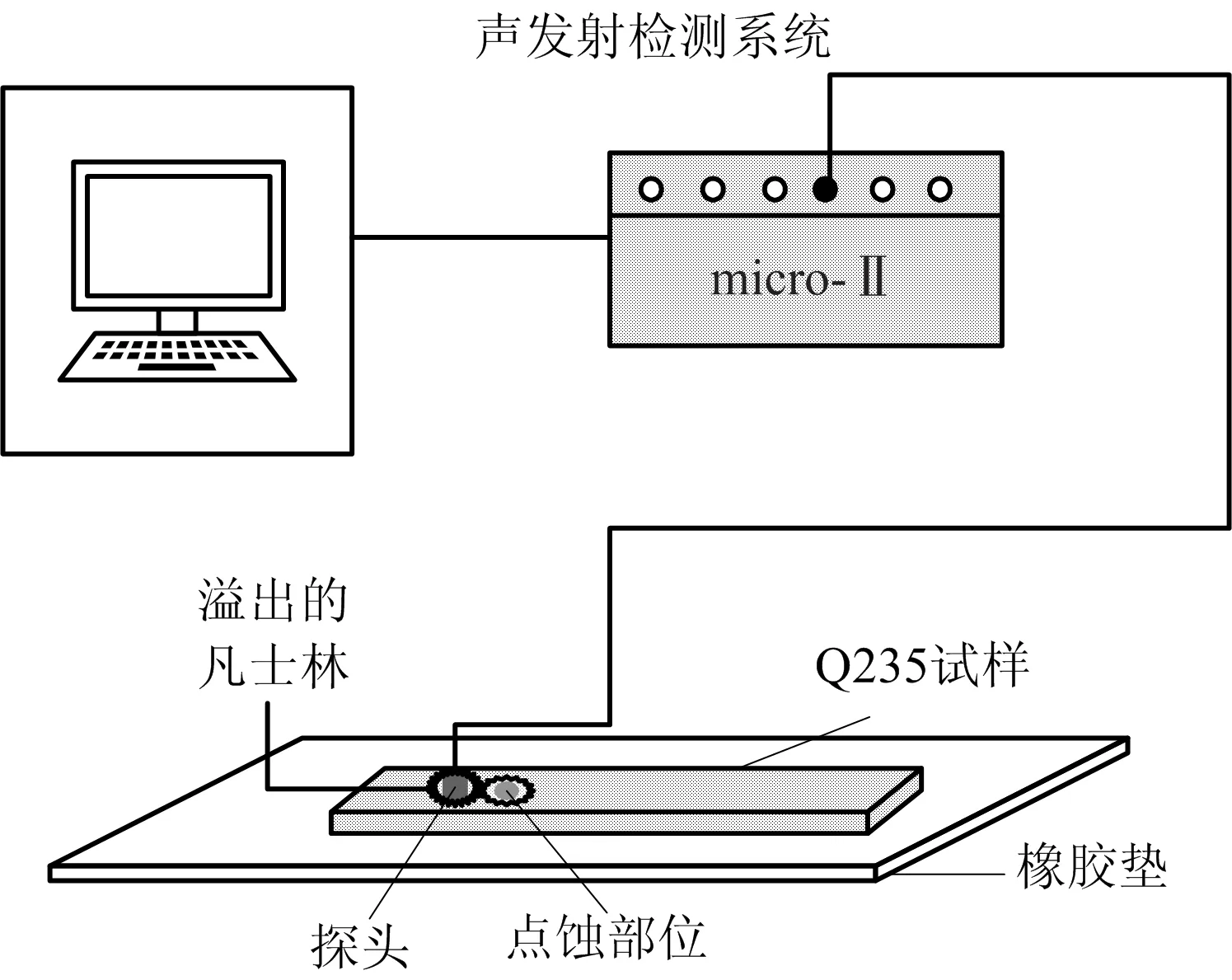
图2 声发射检测工作示意Fig.2 Schematic diagram of acoustic emission detection

1.3 实验结果

整个实验进行6 h，将采集到的信号数据按时间先后顺序每间隔2 h进行分组，标位前中后3种状态，采用Matplotlib在Jupyter notebook中进行可视化处理，如图3所示，整个过程产生丰富的声发射信号。从频域角度进行分析可知，前期频带较宽，主要分布在250～2 000 Hz，最大幅值为0.025 mV，能量较分散；中、后期声发射信号频带分别分布于250～700 Hz和250～900 Hz，频带较窄并均集中在低频区域，最高幅值分别为0.005，0.01 mV，能量较集中。

图3 点蚀前中后期频谱Fig.3 Spectrum of early,middle and later period of pitting corrosion

2 数据采集及预处理

本文选取6个典型声发射特征参数和2个衍生声发射参数RA和RD。其中,RA值为上升时间与幅度的比值，表征信号的斜率，RD为上升时间与持续时间的比值，表征信号波形的陡峭程度。

由于声发射信号特征参数类型和个数的选择直接影响聚类结果，所以本文对提取的所有特征进行相关系数法，剔除相关性大的特征。

相关公式如式(1)～(2)所示：

(1)

(2)

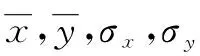
8个特征参数的相关系数矩阵见表1，绝对能量与能量强相关，绝对能量包含的声发射信息小于能量包含的声发射信息，删除绝对能量；RA与上升时间强相关，但上升时间受采集阈值影响较大，删除上升时间。因此，本文选取计数、能量、持续时间、幅值、RA、RD这6个特征参数输入聚类分析。

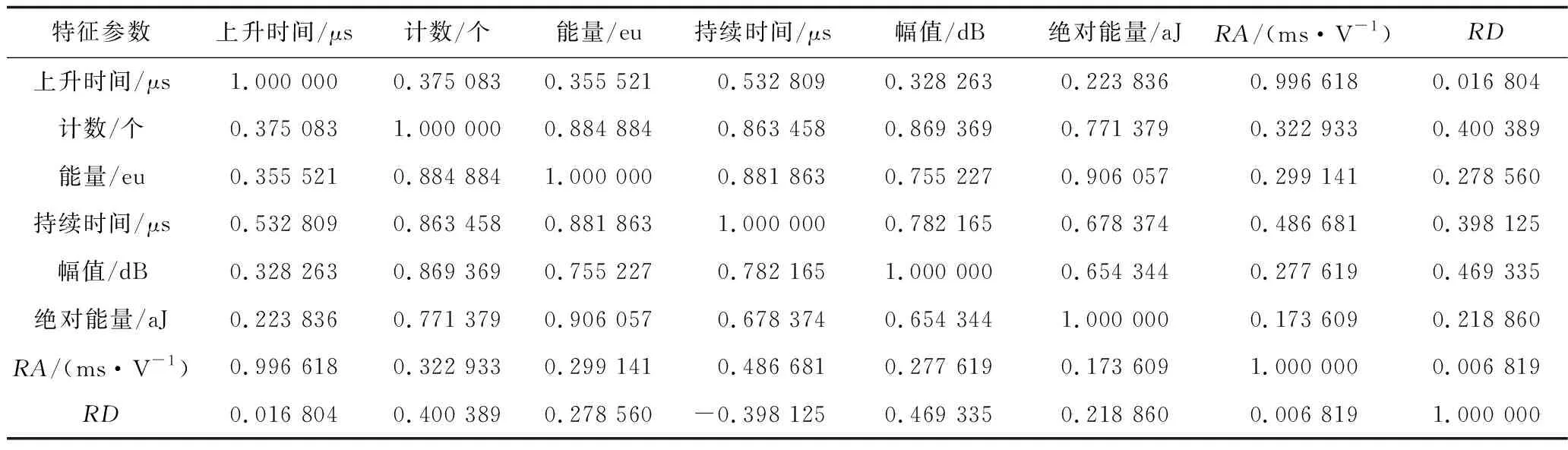
表1 特征参数相关系数矩阵Table 1 Correlation coefficient matrix of characteristic parameters

3 基于改进K-means的CNN故障诊断流程

基于改进K-means的CNN故障诊断流程如图4所示，首先采集点蚀声发射信号，并预处理选取特征参数，再通过肘部法则确定该数据集的最佳k值，结合聚类确定声发射源类别个数，建立CNN模型，输出类别诊断结果及准确率。

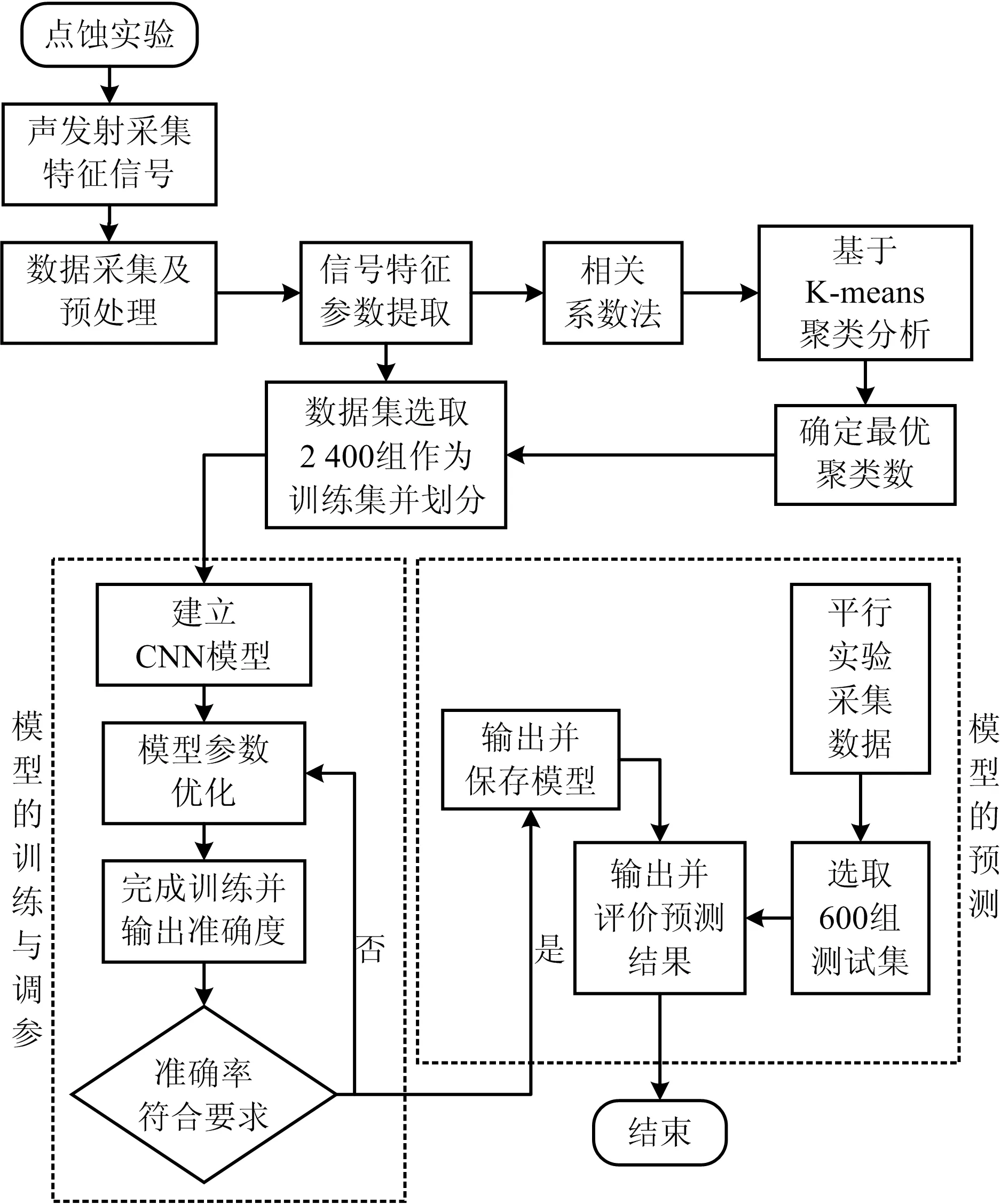
图4 基于改进K-means的CNN故障诊断流程Fig.4 CNN fault diagnosis process based on improved K-means

3.1 基于肘部法则的K-means聚类分析

K-means算法是以最小化样本与质点平方误差作为目标函数，当目标函数达到最优化，表示达到聚类目的。但目标函数中需要确定类簇个数，传统个数通过经验得到，缺乏客观性，因此，本文加入肘部法则，保证k值选取的准确性。

1)肘部法则

将每个类别与其类中心点的距离称为畸变程度，畸变程度随类别数增加而降低，在某个临界点，畸变程度改善效果突然大幅度变化，表明此处聚类效果较好。肘部法则运用该思想确定最佳聚类数，体现在曲线最显著的拐点，即表示正确的类别数。

2)最佳聚类个数确定

本文运用CH指标、轮廓系数指标和SSE指标作为表征畸变程度的损失函数，结合肘部法则选取k值。3种聚类评估指标计算如式(3)～(5)所示。

①CH指标

CH越大表示类自身越紧密，类与类之间越分散，即聚类结果更优，如式(3)所示：

(3)

式中：N为数据集样本点的个数；k是类别个数；Bk是类别之间协方差矩阵；Wk是类别内部数据协方差矩阵；Tr为矩阵的迹。

②轮廓系数(S)指标

轮廓系数是对类中所有数据点紧密分组程度的度量，轮廓系数分值越高，分类效果越好，如式(4)所示：

(4)

式中：a代表同类中2点的均值；b代表1个点至除自身所在类外最近类的样本间均值。

最后所有样本的S(i)的均值称为S，也就是轮廓系数[11]。

③误差平方和(SSE)指标

SSE代表聚类效果的优劣，SSE值越小，说明各类之间分隔越明显，聚类结果越好[12]，如式(5)所示：

(5)

式中：Ci是数据点完成聚类后的第i类；p是Ci中的样本点；mi是Ci中所有样本数据点距离的均值；k为聚类数。

不同损失函数对应误差平方和随k值变化曲线如图5所示，当聚类个数k增大，误差平方和均逐渐减小，且在k=3时，有明显转折点，转折点3就是最佳聚类个数。

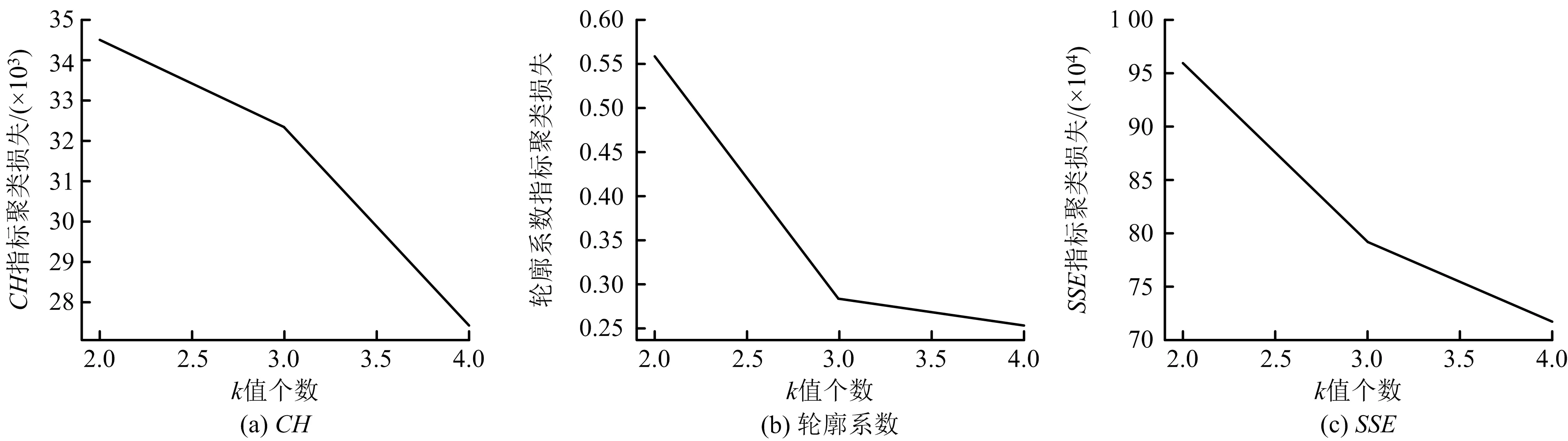
图5 误差平方和随k值变化的曲线Fig.5 Curves of sum of squares of errors varying with k value

3)聚类分析结果

k=3时，衍生特征值RA，RD随时间分布3D如图6～7所示，4个典型特征值随时间分布如图8所示。

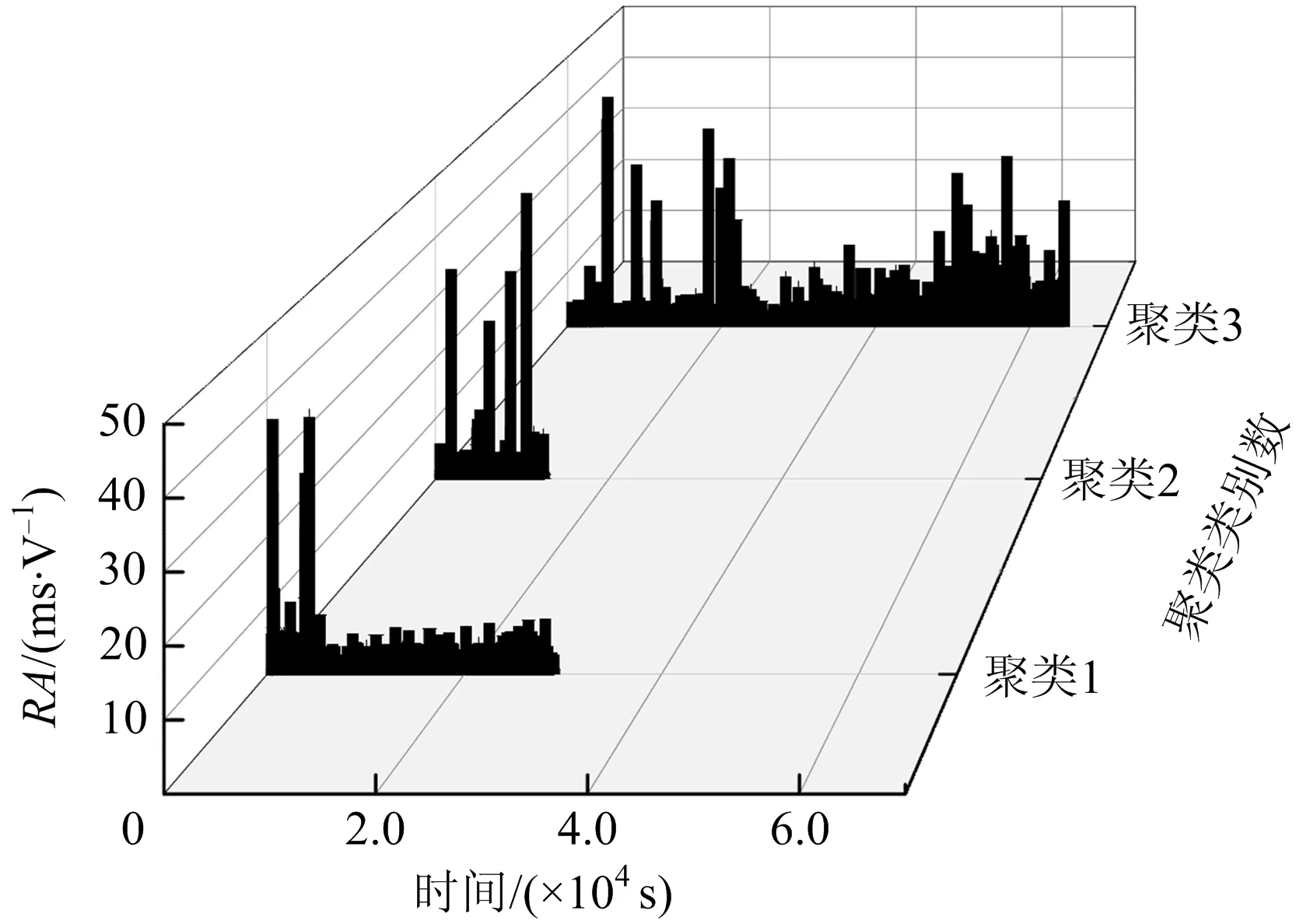
图6 RA随时间的聚类分布Fig.6 Clustering distribution of RA over time

图7 RD随时间的聚类分布Fig.7 Clustering distribution of RD over time

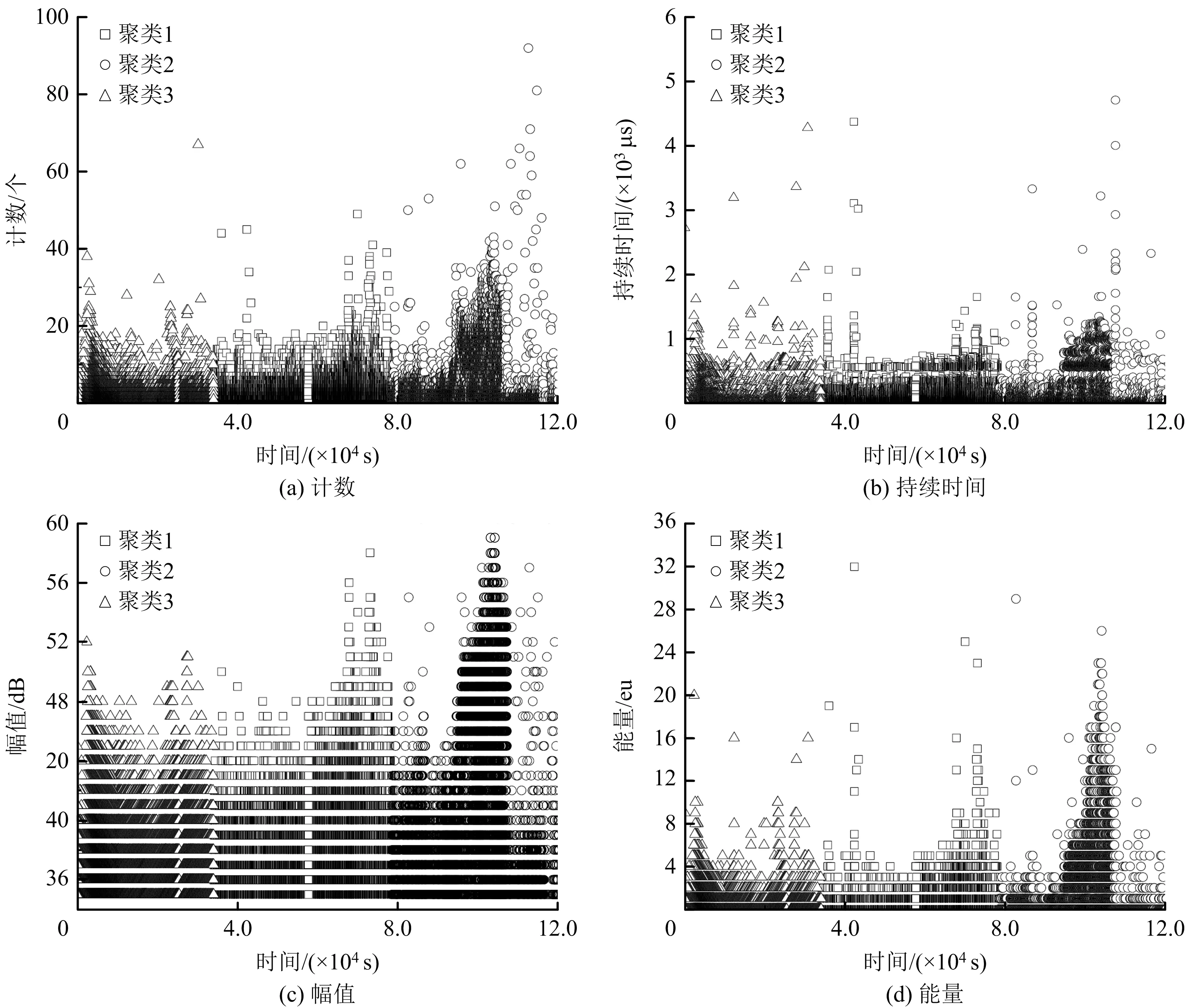
图8 4个典型特征值随时间的聚类分布Fig.8 Clustering distribution of 4 typical characteristics values over time

由图8可知，前期聚类1能量最小，计数最少，幅值相对较小，持续时间相对最短，是典型的脉冲型突发信号，理论上气泡破裂会产生脉冲型信号，通过该特征确定这类信号为点蚀前气泡破裂产生的声发射信号；中期聚类2能量较高，幅值相对最高，持续时间较长，计数相对最大，理论上开裂或蚀坑扩展时信号最活跃，即计数和能量相对最高，可以判定聚类2是腐蚀开裂、相邻点蚀坑贯穿生长和扩展产生的声发射信号；后期聚类3持续时间较长,但幅值较低，能量值较大，体现为较明显的连续型声发射信号特征，理论上腐蚀产物层间摩擦和自身开裂均会产生连续型声发射信号，因此，聚类3为腐蚀产物层间摩擦和开裂产生的信号[13]。

3.2 一维卷积神经网络识别模型

1)一维卷积神经网络模型结构

本文提出的罐底点蚀卷积神经网络模型结构参数如表2所示。为加快收敛速度，激活函数设置为Relu，第1层卷积层由大小为3的卷积核以及64个过滤器组成，为减少输出的复杂性并防止数据过拟合，加入大小为3的最大值池化层；输出矩阵大小为输入矩阵的1/3；再者为均值池化层和Dropout层，为随机去除50%神经元，避免过拟合发生，设置Dropout为0.5[14]；平坦层中Softmax作为激活函数，强制模型最后3个输出值总和为1。

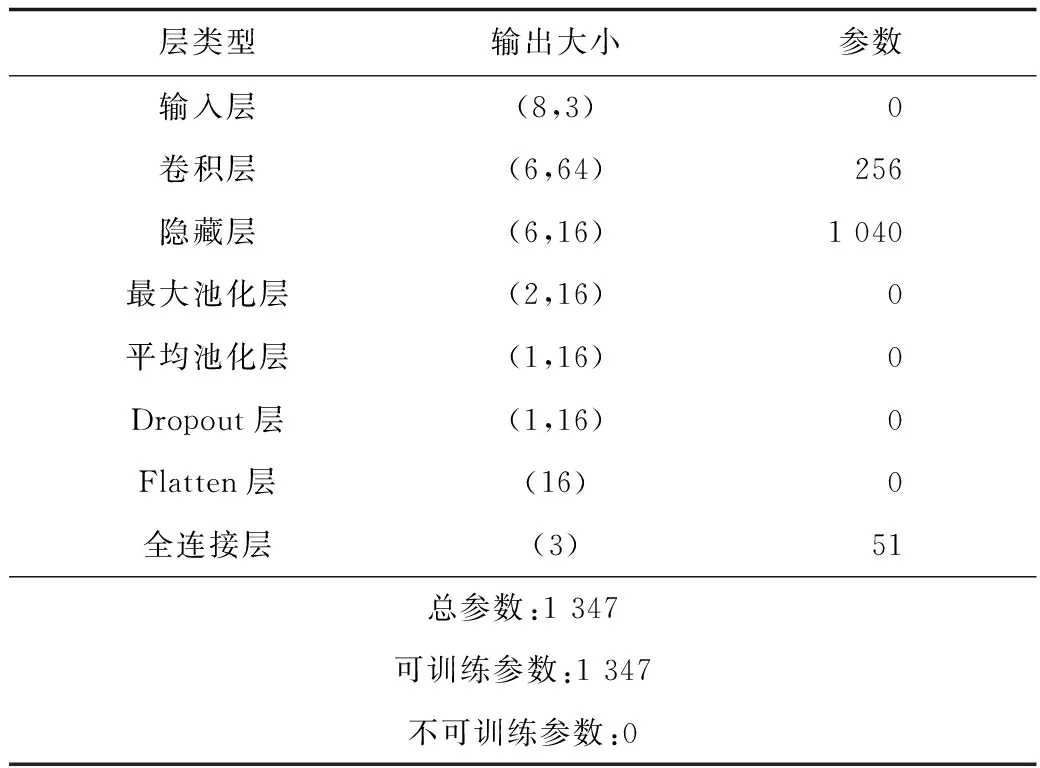
表2 模型结构参数Table 2 Structural parameters of model

2)实验结果分析

随机从聚类结果中抽取2 400组数据，每个类别的数据组个数不相等，将所有数据输入基于Tensorflow的CNN模型，设置该模型批处理量为20，共执行100个训练周期。训练完成后，用Matplotlib对训练集和验证集准确率和损失函数进行可视化分析，如图9所示。

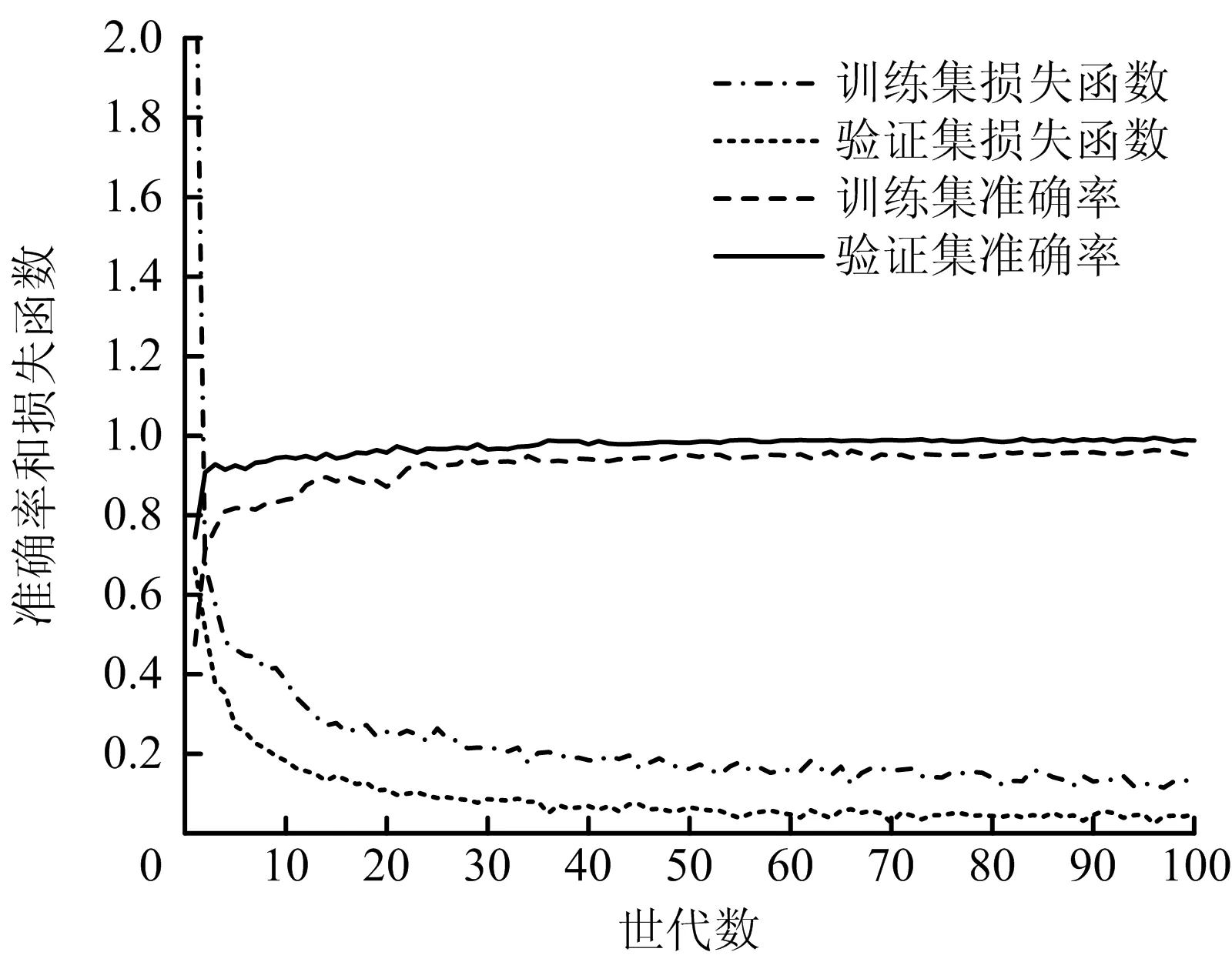
图9 模型准确率和损失函数变化曲线Fig.9 Variation curves of model accuracy and loss function

由图9可知，曲线在整个训练过程中没有太大波动。25世代后，训练集与验证集的准确率曲线基本保持一致并慢慢趋于稳定，准确率保持在98%左右；损失函数在0～0.2之间存在小范围波动，鲁棒性较高。综上，说明模型准确率较高，误差较小。

为进一步验证模型准确性，进行多组平行实验。随机抽取3类声发射源信号，共600组，每组抽取的声发射源样本个数不相等。利用已训练好的CNN模型，识别平行实验采集到的声发射信号，得到混淆矩阵如图10所示，聚类1识别准确率达100%，其余2个类型的识别准确率达99%，说明该CNN模型能够有效对储罐底板点蚀声发射源进行识别，准确率较高。

图10 600组测试集的混淆矩阵Fig.10 Confusion matrix of a 600-group test set

4 结论

1)肘部法则结合CH、轮廓系数和SSE3种聚类评估指标选取k值，提高聚类算法的可信度；通过分析各特征参数随时间变化的聚类分布，将点蚀数据分为3种信号类别，解决点蚀数据难以准确获得类别标签的难题。

2)一维卷积神经网络模型可将点蚀原始声发射信号直接输入，对点蚀过程中3类声发射源进行准确区分，准确率平均高达99%。

3)本文模型对现场常压储罐底板腐蚀声发射检测定量分析具有指导作用，可以将此模型与现场检测相结合，应用于日常检测。当现场检测无法确定点蚀程度时，将出现持续时间长、幅值较低、能量值相对较大的声信号特征，且模型输出结果聚类标签大部分为点蚀后期，此时需要重点关注运行过程和未来开罐检测，进而确定最佳开罐周期，降低储罐检测成本和运行风险。