火灾下钢筋混凝土梁热力学性能数值模拟分析*

刘朝峰，孙一鑫，王 玲，周 宝，刘才玮，刘倩倩

(1.河北工业大学 土木与交通学院,天津 300401； 2.青岛理工大学 土木工程学院,山东 青岛 266033)

0 引言

钢筋混凝土(Reinforced Concrete,RC)结构构件在火灾高温作用下，其内部钢筋、混凝土等材料的力学性能退化与钢混界面黏结退化导致结构承载能力衰减或丧失[1-2]。外部混凝土高温爆裂导致结构构件质量损失，也会降低结构的承载力和耐火性能[3]。因此，有必要开展火灾高温下RC结构构件热力学性能研究。

钢筋、混凝土等材料及组成的构件常温与高温后力学性能得到了较为充分的研究[4-5]。然而，火灾高温下RC梁的热力学性能及影响因素研究却不够系统。火灾高温下/后结构或构件的力学性能退化程度研究还需要考虑混凝土爆裂导致结构温度场变化引起的抗火性能退化。张岗等[6]利用数值模型分析了爆裂对预应力混凝土箱梁截面温度场的影响，指出高温极限抗弯承载能力在混凝土不同爆裂深度下的衰变表现为多阶段特征。许文龙[3]通过数值分析模型研究混凝土高温爆裂参数对截面温度场、抗弯承载力的影响规律，指出爆裂深度、爆裂面积比和爆裂位置均对截面温度场和承载力有一定的影响。王富强[7]采用有限元建模分析不同火灾场景后RC柱式桥墩的剩余极限承载力，提出考虑混凝土爆裂的RC柱式桥墩剩余承载力衰变计算公式。Ren等[8]提出了1种活性粉末混凝土梁的改进高温爆裂判据，建立了有限元模型研究了构件的火灾行为，发现改进的爆裂判据能够准确地预测高温爆裂发生和防火性能。Mróz等[9]提出1种利用混凝土发出的声信号来识别剥落形式和强度的新方法。

高温下钢筋与混凝土界面黏结退化对结构的耐火性能有很大影响，而在数值模拟分析中多将钢筋与混凝土之间假定为完全黏结，与实际情况存在较大差异[10]。Song等[11]通过钢筋拔出试验指出滑移量与峰值应力呈正比关系。Kodur等[12]通过数值模型和火灾试验证明了高温下黏结滑移对RC梁的强度退化程度和挠度有很大影响，会降低梁的抗火性能。Huang[2]结合火灾试验和模型验证指出钢筋温度达到500 ℃时，黏结状态严重退化，对结构的耐火性能有很大影响。鉴于此，本文采用经试验验证的数值分析模型分析不同受火时间、混凝土爆裂、钢筋与混凝土黏结退化等因素对RC梁截面温度场分布、钢筋应力与滑移量分布、残余抗弯承载力的影响规律，拟为钢筋混凝土梁火灾高温损伤评估提供参考。

1 RC梁数值分析模型

1.1 几何参数与物理属性

设计制作4根全尺寸的钢筋混凝土试验梁[3]，试验梁总长为3 000 mm，支座中心距梁体端部为100 mm，试验梁截面为250 mm×400 mm，混凝土保护层厚度为30 mm，受力纵筋、架立筋为HRB400级带肋钢筋，箍筋采用HPB300级钢筋，纵筋长度2 940 mm。试验梁左端为固定铰支座，右端为可动铰支座。混凝土采用C35的硅质混凝土。截面尺寸如图1(a)所示，配筋构造情况如图1(b)所示。

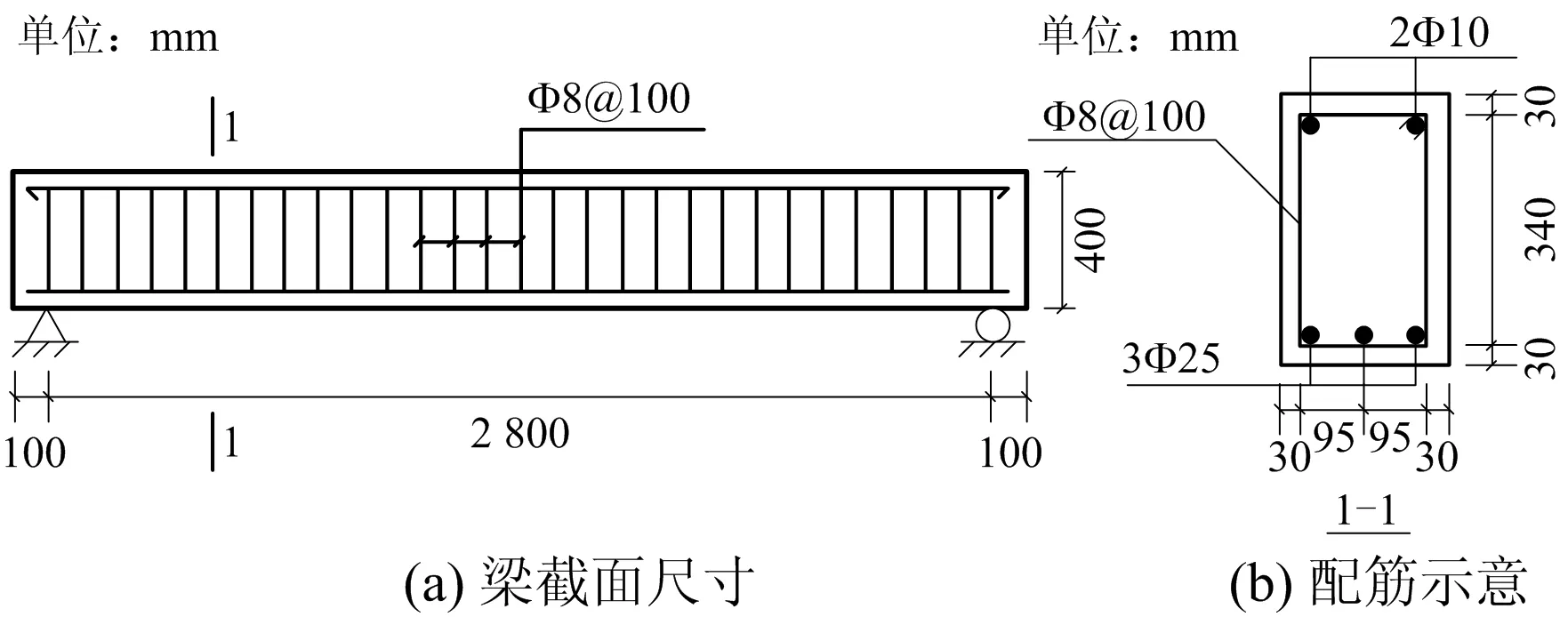
图1 构件尺寸与配筋Fig.1 Member sizes and reinforcement

根据《建筑钢结构防火技术规范》(GB 51249—2017)[13]中的标准ISO834升温曲线对4根试验梁，编号：L1，L2，L3，L4，分别进行不同受火时间，即60，90，120，150 min的火灾试验。火灾试验中梁截面温度场分别利用跨中截面和靠近固定铰支座1/3跨截面处布置的6个K型热电偶测得，编号及位置如图2所示。每隔1 min用数据采集仪记录1次测点温度数据。

图2 试件尺寸与热电偶布置示意Fig.2 Measuring points arrangement of section temperature

模型中钢筋、混凝土的物理属性采用实测值，纵筋、架立筋屈服强度为468 MPa，箍筋屈服强度为360 MPa，钢筋弹性模量为200 MPa；混凝土轴心抗压强度实测值取40.7 MPa，混凝土弹性模量为31.5 GPa。

1.2 数值分析模型构建

本文采用顺序耦合分析法对高温下RC梁热力学特性进行研究，数值分析模型构建如下：

1)温度场分析：对RC钢筋混凝土梁进行标准火灾升温传热分析，获得RC梁不同截面温度场。混凝土采用DC3D8三维八节点六面体线性传热单元，钢筋采用DC1D2一维二节点线性传热单元。钢筋和混凝土之间选用tie约束。钢筋和混凝土的初始温度设置为20 ℃，斯蒂芬玻尔兹曼常量和时间相关，以min为单位时的取值为3.402×10-6J/(m2·min·K4)，绝对零度取-273.15 ℃；RC梁三面受火(底面和2个侧面)，梁体顶面和梁端至支座100 mm范围不受火，设置受火面处对流换热系数取2 100 J/(m2·min·℃)，辐射换热系数取0.8，而非受火面处的对流换热系数取600 J/(m2·min·℃)。升温制度采用《建筑钢结构防火技术规范》(GB 51249—2017)[13]中的ISO834标准升温曲线。

2)力学性能分析：基于已有温度场，确定不同材料高温下/后的力学性能，模拟考虑混凝土爆裂的RC梁的力学行为。数值分析时，混凝土采用C3D8R八节点六面体减缩积分单元，钢筋采用T3D2桁架单元，钢筋与混凝土黏结滑移行为采用非线性弹簧单元模拟，参考文献[2]；设置纵向钢筋与混凝土的黏结滑移之前，要解除纵向钢筋与混凝土间的嵌入式约束关系，在钢筋和混凝土节点处添加三向节点弹簧。假定箍筋与混凝土之间黏结良好。建立的数值分析模型的节点编号、网格尺寸与温度场分析时保持一致。

3)爆裂数值分析：混凝土高温爆裂可采用“生死单元”来模拟，但需在温度场分析模型做以下修改：①在part模块中切分出混凝土爆裂工况，创建混凝土爆裂单元集合；②在分析步模块中分别设置混凝土爆裂前升温时间和爆裂后剩余升温时间；③在相互作用模块使用Model Change杀死发生爆裂的混凝土单元，梁体新受火面重新设置边界条件，如图3所示。

图3 混凝土梁爆裂模型示意Fig.3 Schematic diagram of concrete beam bursting model

1.3 热本构关系与热工参数

火灾试验炉内RC梁在升温过程中属于瞬态传热过程，一般由热传导、热对流和热辐射方式任意组合传递热能。RC梁表面及内部温度场分析基于热传导的基本方程[14]，如式(1)～(2)所示：

(1)

(2)

式中：Q是试验梁从外部获得热量,W；k是导热系数[m/m·℃]；T是温度,℃；Γ是传热面；n是传热面的外法线；hc和ε分别是对流系数和辐射系数；Tf和Tc分别是环境温度和RC梁表面温度；σ=5.67×10-8W·m-8·K-1，是斯特藩-玻尔兹曼常量；ρ是密度，kg/m3；c是比热容，J/(kg·C)；t是时间，s；q是RC梁内部产生的热量，在传热分析中q=0 J。

高温导致混凝土密度变化较小，故混凝土密度ρc取2 500 kg/m3，比热容Cc取921.14 J/(kg·℃)，热传导系数λc、热膨胀系数αc随温度变化公式[15-16]，如式(3)～(4)所示：

(3)

αc=(6+0.008T)×10-6

(4)

高温对钢筋力学性能及热工性能影响显著，对钢筋密度ρs影响不明显，故取7 800 kg/m3，钢筋热传导系数λs,J/(m·min·℃)、比热容Cs、热膨胀系数αs,[m/(m·℃)]随温度变化公式[15-16]，如式(5)～(7)所示：

(5)

Cs=473+20.1×10-2T+38.1×10-5T2

(6)

(7)

由于试验设备及操作技术等影响因素，会导致火灾试验实际升温曲线与标准升温曲线存在差异，本文采用等效爆火时间[17]作为数值模拟升温时间输入参数，换算关系如式(8)所示：

(8)

式中：te是等效爆火时间,s；f是全盛期火灾持续时间,min；T0是试验炉内气体初始温度,℃；Tgm是试验炉内气体最高温度,℃。

1.4 本构模型与高温下参数

本文分别采用耦合材料高温退化效应的混凝土塑性损伤模型[18]、二折线弹性-强化模型[18]来描述RC梁高温下混凝土和钢筋的力学行为。数值分析模型中高温下的混凝土强度，如式(9)所示。高温下钢筋强度如式(10)所示、弹性模量等参数退化规律详见文献[18]，混凝土和钢筋的泊松比分别取0.2，0.3。

(9)

(10)

1.5 钢筋/混凝土黏结滑移本构

火灾下钢筋混凝土构件中钢筋与混凝土黏结性能会随温度升高而退化，但实际火灾试验难以获得其精确的黏结-滑移规律。一些学者通过小尺度试件高温拉拔试验总结多种黏结滑移本构关系，本文采用文献[2]带肋钢筋高温黏结滑移退化规律，如式(11)所示。局部黏结滑移本构关系采用欧洲规范(CEB-FIP1990)中模型。设置纵向钢筋与混凝土的黏结滑移之前，要解除纵向钢筋与混凝土间的嵌入式约束关系。

(11)

2 数值分析模型验证

为了验证RC梁数值分析模型的有效性，将试验梁L3，L4高温下数值模拟结果与火灾试验结果进行对比。RC梁L3，L4在不同升温时间下截面温度测点实测值与模拟值对比如图4所示，其中带“*”表示模拟值。

图4 温度测点的实测值与模拟值Fig.4 Measured and simulated values of temperature measuring points

各测点温度实测值与模拟值曲线升高趋势基本一致，表明本文数值分析模型的有效性和可靠性。但1#，2#，4#测点温度在受火前期升温速率较快；各测点的温度实测曲线均出现温度平台现象，主要是混凝土中水分蒸发迁移和“饱和蒸汽带”形成导致热量散失或阻碍热量传导；而模拟温度曲线均较为平滑，未出现温度平台现象，主要是数值模拟没有考虑水分蒸发迁移及所选取的热本构关系的影响；6#测点的实测值与模拟值曲线差别较大，可能是火灾试验时采用防火岩棉对炉盖进行封堵，可能岩棉部分覆盖6#测点位置或是炉盖密封不严导致热量散失，引起6#测点实测温度比模拟值较低。

3 结果分析与讨论

3.1 温度场分析

图5和图6分别为不同受火时间下试验梁跨中截面温度场云图和钢筋温度场云图。

图5 不同受火时间下试验梁跨中截面温度场云图Fig.5 Cloud map of temperature field at mid-span section of test beam under different fire durations

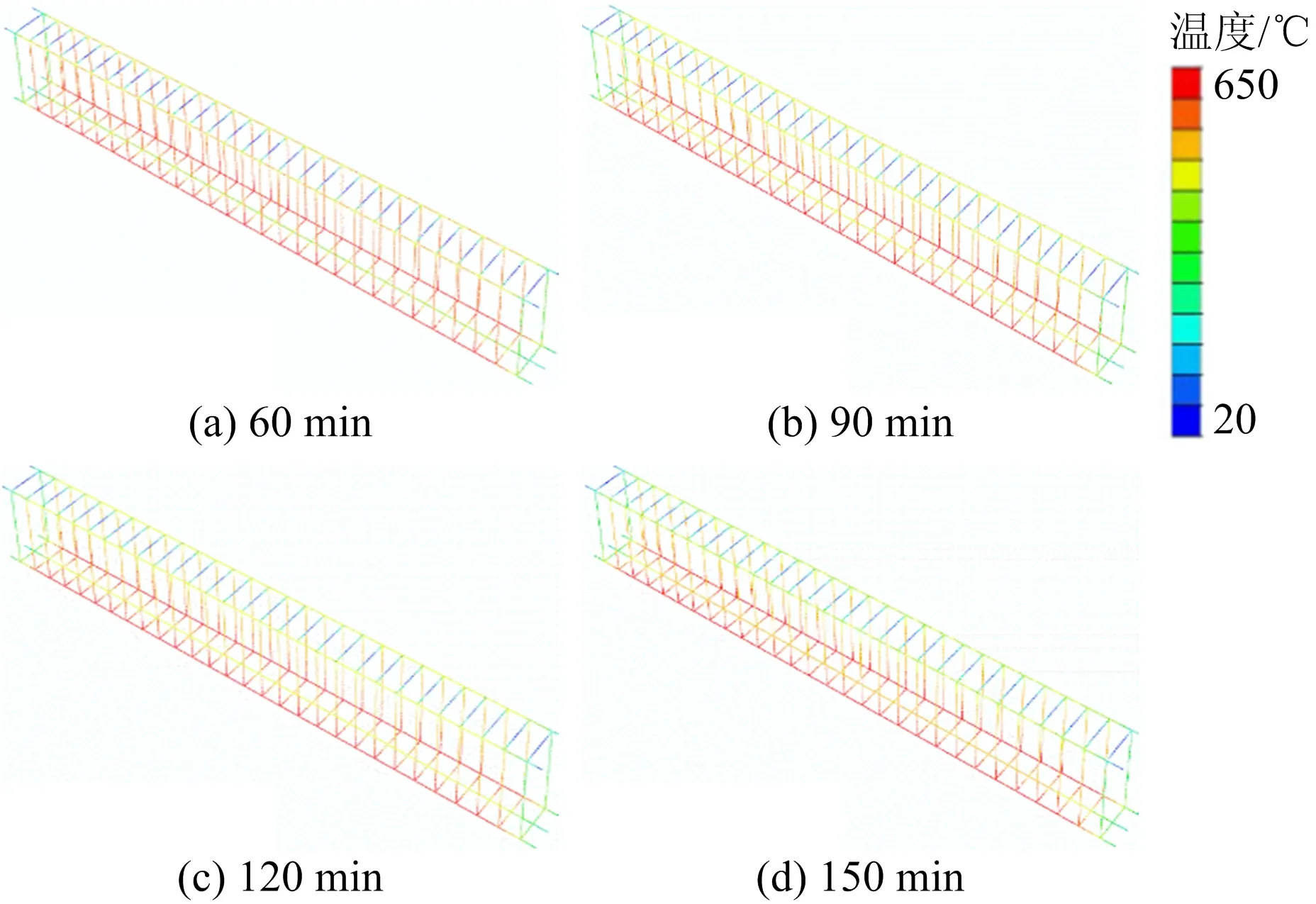
图6 不同受火时间下试验梁跨中截面钢筋温度场云图Fig.6 Cloud map of temperature field at mid-span section of test beam under different fire durations

由图5可知截面温度场呈现梯度分布，且随着受火时间的增大，截面温度梯度逐渐扩大，受高温的影响区域相对比例逐渐增大，主要是混凝土的热惰性特征延缓了截面核心区域升温过程。截面角部附近温度最高，钢筋骨架中底部角筋温度最高，主要是由于该位置处于2个受火面交界处，积累2个受火面传导的热量，温度相互叠加耦合，导致该位置的温度比其他位置均较高，最终等温线逐步发展成光滑的U型。

为细化分析爆裂参数对截面温度场的影响，结合试验情况设定数值模拟工况参数如表1，爆裂区域位置如图7所示。

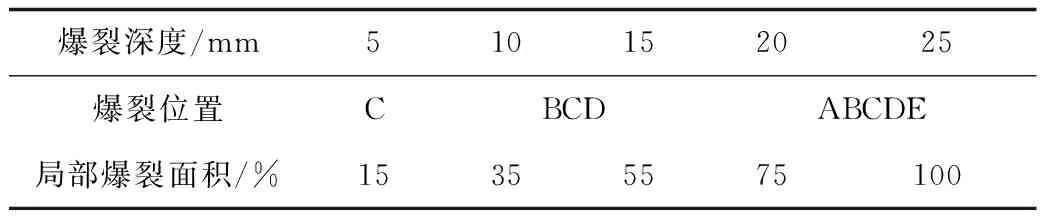
表1 爆裂特征参数设计Table 1 Design of bursting characteristics parameters

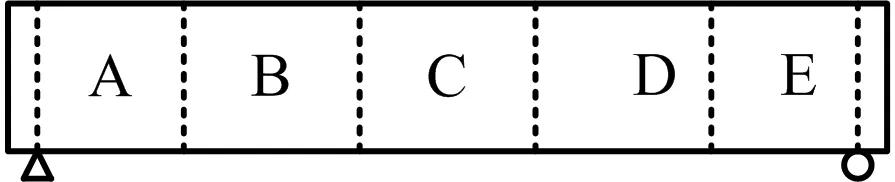
图7 爆裂位置分区示意Fig.7 Schematic diagram of bursting location zoning

根据相关文献研究及试验观测，将爆裂集中发生设定在受火15 min，受火时长为120 min，采用控制变量法分析爆裂参数对截面温度场的影响程度，详见文献[3]。数值模拟分析可知，混凝土爆裂对直接受火底面以内10 mm范围的温度影响较明显，随着到直接受火面距离的增大，截面测点的温度影响迅速减小。因此，截面钢筋处的温度存在较大温差现象。随着爆裂面积比的增大，其对截面温度场的影响逐渐变小，超过15%之后基本上可以忽略其影响。截面的侧面爆裂高度对截面测点温度的影响呈现“以某测点为中心，25%侧面高度范围内发生爆裂对其温度影响较为显著，占全截面爆裂下温度值的80%左右”特点。

如图8所示，图8为跨中截面底部角筋温度随爆裂深度变化曲线。随爆裂深度增大，相同受火时刻下角筋的升温速率越快。混凝土爆裂10 mm比爆裂5 mm时温度增加了7.4%，爆裂15 mm比爆裂10 mm时增加了7.8%，爆裂20 mm比爆裂15 mm时增加了8.2%，爆裂25 mm比爆裂20 mm时增加了8.7%。

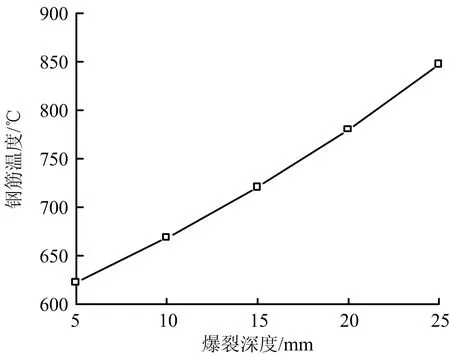
图8 跨中截面角筋温度随爆裂深度变化曲线Fig.8 Variation curve of temperature of corner tendons at mid-span section with bursting depth

3.2 钢筋应力与滑移分析

钢筋应力水平在一定程度上可以反映出钢筋混凝土梁抗弯承载力退化情况。在外部荷载和火灾高温共同作用下钢筋周围的混凝土可能出现裂纹和局部爆裂等损伤，底部纵筋承担主要拉应力。通过位移加载至极限承载力状态，得到试验梁不同升温时间下受拉纵筋的应力分布如图9所示。

由图9可知，1)试验梁跨中底部中筋的应力高于底部角筋，主要是因为角筋受到来自2个受火面传导的热量，温度会相互耦合，导致角筋力学性能和钢筋-混凝土黏结性能退化。2)2个加载点之间的钢筋应力分布呈“马鞍”状，靠近梁右端的加载点处对应的钢筋应力水平较高，主要是梁体右端部为可动铰支座，会发生水平位移，导致底部纵筋拉伸变形更大。3)随着受火时间的增长，钢筋/混凝土黏结性能退化越来越恶劣，考虑黏结滑移的钢筋应力分布曲线逐渐由包络线变为被包络线；底部角筋与中筋的应力水平随受火时间增长而呈现不同下降趋势；以梁跨中1.5 m位置处钢筋应力为例，角筋应力水平：受火90 min比受火60 min下降了6.3%，受火120 min比受火90 min下降20%，受火150 min比受火120 min下降27.1%；中筋应力水平：受火90 min比受火60 min下降了40%，受火120 min比受火90 min下降33.3%，受火150 min比受火120 min下降30%。

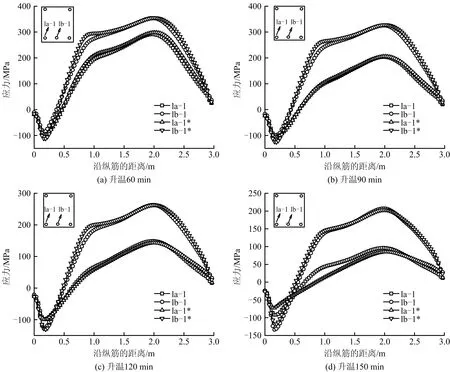
注：“*”表示考虑黏结滑移情况图9 不同升温时间下受拉纵筋的应力分布Fig.9 Stress distribution of longitudinal tendons in tension under different heating time

如图10所示，为不同受火时间下钢筋与混凝土之间滑移量分布图。由图10可知：1)RC梁受火时间越长，经历温度越高，钢筋与混凝土之间的黏结滑移量越大；2)钢筋与混凝土之间的最大滑移量出现在固定支座附近(左端)，最小滑移量出现在可动铰支座附近(右端)。主要原因是高温导致钢筋强度降低、热膨胀变形，固定支座处混凝土水平向自由度受限，引起钢筋与混凝土之间变形不协调，相对滑移量较大，而可动支座处钢筋与混凝土在水平方向可共同移动，故相对滑移量较小；3)截面底部中筋的滑移量小于角筋，主要是因为角筋受到2个受火面的热量，温度相互耦合叠加，导致其经历的温度最高，与混凝土黏结强度退化更加严重。

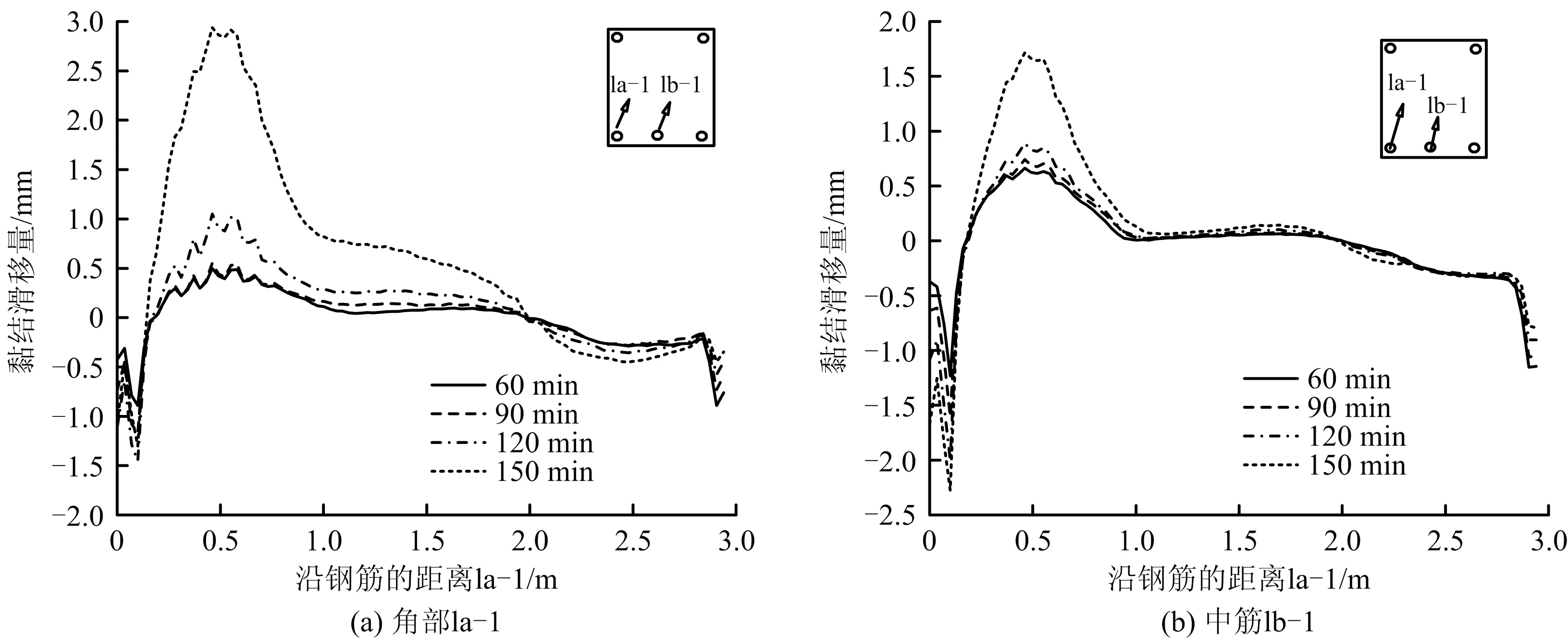
图10 底部纵筋滑移量分布Fig.10 Distribution of bottom longitudinal tendons slip amount

3.3 抗弯承载力分析

由于火灾下钢筋混凝土梁的残余抗弯承载力不便于测得，本文采用数值模拟与理论简化计算方法[17]进行对比分析。首先，数值建模仅考虑高温下钢筋/混凝土黏结滑移退化，不同受火时间下钢筋混凝土梁的抗弯承载力，如图11所示。随着升温时间的增加，钢筋混凝土梁的抗弯承载力下降速率明显，基本上呈现线性下降趋势，受火150 min时的抗弯承载力比60 min时下降了约46%。

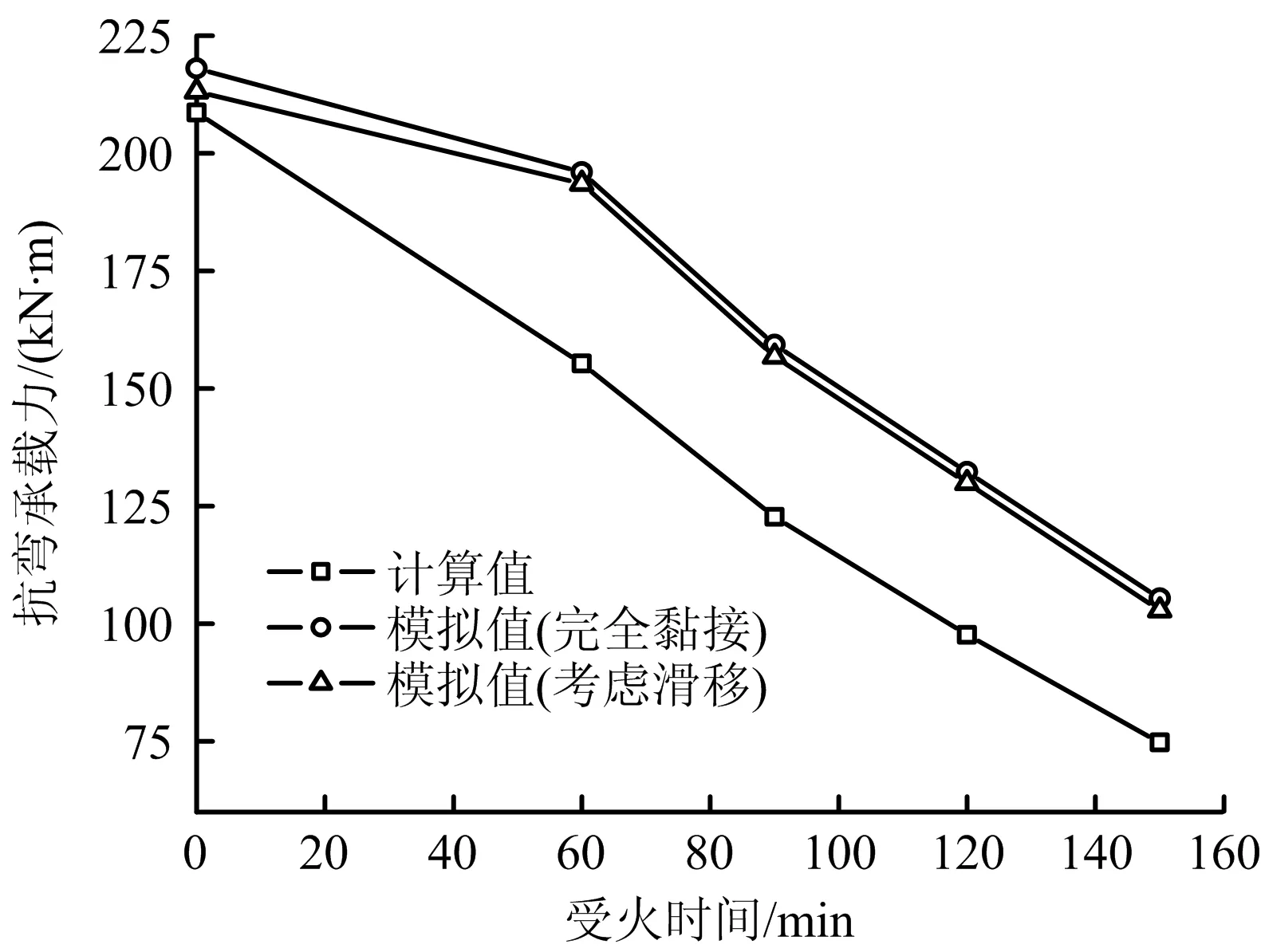
图11 梁的抗弯承载力计算结果Fig.11 Calculation results of flexural bearing capacity of beam

其次，为了进一步探究不同爆裂参数组合对高温下钢筋混凝土梁抗弯承载力的影响规律，本文采用控制变量法，设置升温总时间为120 min、爆裂时刻为升温第15 min、受火面三面全爆裂为不变量，爆裂的位置、爆裂深度和局部爆裂面积比为变量，爆裂位置对称分布取C，BCD，ABCDE 3种情况，如图7所示，每组进行50次模拟计算，得到高温下混凝土爆裂参数与混凝土梁残余抗弯承载力的关系，如图12所示。

在爆裂面积和爆裂深度组合时，爆裂面积和深度愈大，则残余抗弯承载力越低；爆裂位置为C时，试验梁的抗弯承载力下降幅度较大，当爆裂位置扩展到BCD时下降的程度逐渐减弱，扩展到AB，CDE全截面爆裂时其抗弯承载力与BCD位置时几乎一致，表明试验梁的跨中C区域爆裂对结构抗弯承载力影响最大。当爆裂位置确定时，随爆裂深度的增加，抗弯承载力衰减曲线的斜率呈不断增大趋势，而随爆裂面积比增加，抗弯承载力衰减曲线的斜率呈减小趋势；由图12可知，爆裂深度对高温下试验梁残余抗弯承载力的影响程度要高于爆裂面积。综上分析，混凝土高温爆裂会导致工程构件的承载能力衰变，在工程抗火设计中应考虑混凝土爆裂的影响，可从材料及构件2个尺度抑制混凝土爆裂对构件承载力的影响，将是以后持续研究的重点内容。

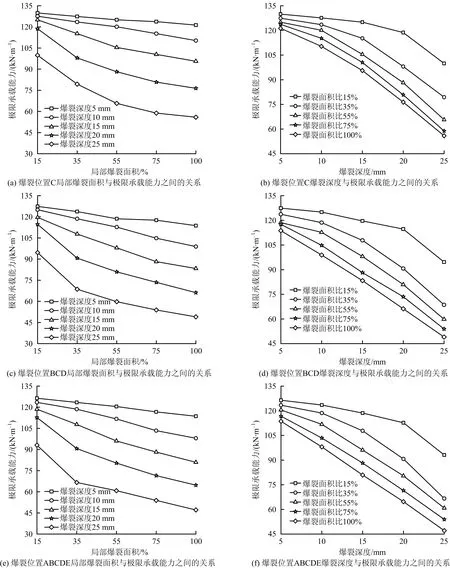
图12 抗弯承载力与爆裂参数关系曲线Fig.12 Relationship curve between flexural bearing capacity and bursting parameters

4 结论

1)火灾下RC梁截面温度场呈现梯度分布，且随着受火时间的增大，截面温度梯度逐渐扩大；底部角筋比其他纵筋升温均快；混凝土爆裂对直接受火底面以内10 mm范围的温度影响较明显，角筋升温速率随爆裂深度的增大而增大。

2)火灾下试验梁跨中底部中筋的应力高于角筋，底部纵筋应力水平随受火时间增长而呈现不同下降趋势；2个加载点之间的钢筋应力分布呈“马鞍”状，靠近梁右端的加载点处对应的钢筋应力水平较高；钢混界面滑移量随受火时间增长而增大，底部中筋的滑移量小于角筋；钢筋与混凝土之间的最大滑移量出现在固定支座附近，最小滑移量出现在可动铰支座附近。

3)高温下RC梁的抗弯承载力随升温时间增长而呈线性下降趋势，受火150 min时的抗弯承载力比60 min时下降了约46%；RC梁的跨中C区域发生爆裂对结构抗弯承载力影响较大；爆裂深度对高温下RC梁残余抗弯承载力的影响程度要高于爆裂面积。