ESSM和Tone方法在熔盐堆共振计算中的适用性分析
戴 明张 奥,2程懋松,2
1(中国科学院上海应用物理研究所 上海 201800)
2(中国科学院大学 北京 100049)
熔盐堆采用高温熔融盐作为燃料,流动的液态燃料分布于石墨构件通道或缝隙、导管外围、下降环腔和上下腔室等位置,复杂的燃料位置分布给共振计算带来了新挑战。随着计算机算力不断提高,采用二维全堆模型加工熔盐堆少群截面成为一种可行方案,这要求共振计算方法适合处理二维全堆级问题,同时能考虑堆芯径向复杂的燃料位置分布、温度分布[1]的影响,且具有良好计算效率[2]。
增强中子流方法[3]结合传统的等价理论或者全局-局部耦合方法[4]是处理压水堆全堆级共振计算的常用方法,上述方法使用Dancoff因子修正,存在几何模型局限性。考虑到熔盐堆中流动燃料的位置分布复杂,本文重点研究不依赖于Dancoff因子修正且适合于复杂几何的全堆级共振计算方法,包括子群法、嵌入式自屏法(Embedded Self-Shielding Method,ESSM)和Tone方法。子群法能有效处理空间共振自屏,也能用于非均匀温度分布问题[5]。Tone方法[6]是针对快堆于1975年提出的基于细群或超细群的共振计算方法,SARAX软件系统使用该方法用于快谱段共振计算[7]。ESSM方法[8]于2011年提出,Tone和ESSM都是基于等价理论的迭代式求解方法,在压水堆中的应用已有相关研究,包括使用均匀共振积分表[9‒10]或非均匀共振积分表[11‒13]。在特定堆型的数值堆中,使用非均匀共振积分表的ESSM和Tone方法能够同时兼顾计算效率和精度。考虑到方法的适用范围,本文重点研究基于均匀共振积分表的ESSM和Tone方法。
基于均匀共振积分表的ESSM或Tone方法需要 较 精 细 的 能 群 结 构 来 保 证 计 算 精 度[9‒10],如SHEM295和SHEM361能群结构。SHEM295能群结构下ESSM和Tone方法能得到相近的结果,且计算效率优于子群法,但计算精度明显差于子群法[9]。Mao和Zmijarevic提出一种新的Tone方法[10],在SHEM361能群结构下可获得与子群法接近的计算精度。精度改进可能来源于两方面的原因:一是SHEM361中4.6~22.5 eV内能群结构细化,因为SHEM295来 源于增大SHEM361的4.6~22.5 eV内能群勒宽;二是新Tone方法采用带子群参数的拟合公式计算有效截面。考虑到新Tone方法并没有计算各子群的通量分布,而使用拟合公式和直接插值没有本质区别,实际的精度改进来源于采用SHEM361能群结构。因此,本文将验证SHEM361能群结构下采用直接插值法的ESSM和Tone方法在熔盐堆栅元共振计算的精度。
考虑温度分布的共振计算是个复杂问题,高精度的求解需要采用基于连续通量的蒙特卡罗方法或基于温度扰动(Temperature Perturbation Technique,TPT)的超细群碰撞概率法[14]。由于上下腔室打混或导流板的存在,在正常工况下熔盐堆堆芯径向温度分布较均匀,但不排除极端堵塞情况下出现较大差异[15]。考虑到全堆级共振计算的规模,本文研究基于等价理论来近似考虑温度分布的影响。Tone方法的均匀截面假设[16‒17]在理论上不适合带温度分布共振计算,但文献[9]中对于带温度分布算例的Tone方法计算结果精度与ESSM方法及均匀温度下的基本相同。文献[10]中新Tone方法并不需要求解子群方程,计算时可同时使用不同温度下子群参数的拟合公式,然而该研究没有评估新Tone方法对存在温度分布的燃料棒计算精度。因此,本文也将评估SHEM361能群结构下基于等价理论的ESSM和Tone方法是否适合带温度分布下熔盐堆共振计算。本文提出了Tone-N方法,它通过额外引入两个固定源方程来考虑其它燃料区影响。
基于ThorLAT栅格计算程序[18],本研究设计和实现了使用均匀共振积分表的子群法、ESSM、Tone和Tone-N共振计算方法。采用SHEM361能群结构,首先通过VERA组件基准题验证共振计算方法实施的正确性,然后针对均匀温度或存在温度分布的通道式熔盐堆燃料栅元进行计算及分析,包括与能群数更少的XMAS172能群结构的结果对比,来初步验证SHEM361能群结构下基于均匀共振积分表插值的ESSM和Tone方法对于熔盐堆的适用性。
1 共振计算理论
1.1 子群法
在共振能区采用窄共振近似,中子通量可表示为:

式中:σp,r为共振核素的势散射截面;σb为背景截面;σ为共振核素的有效总截面。
由式(1)可知,中子通量随有效总截面的改变将远小于其随能量的改变,它是共振核素总截面的平滑函数。子群法即将中子通量对能量的积分转变为对有效截面的积分,该平滑函数可表式为离散形式:
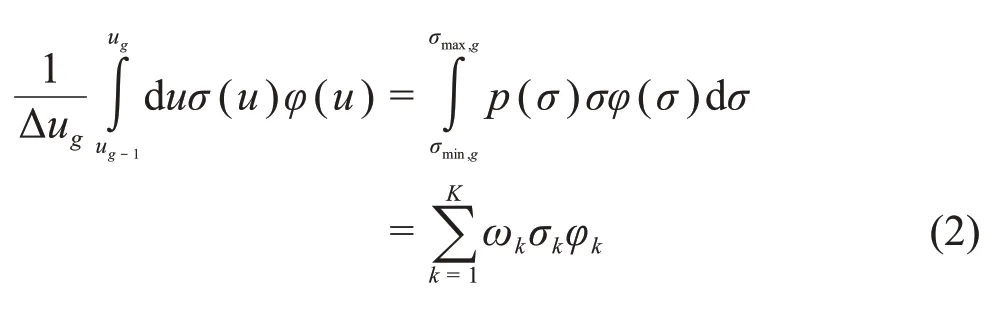
式中:p为能群g内有效截面的概率密度;ωk为子群k权重;σk为子群k截面;φk为子群k通量;K为能群g内的子群数。子群权重和子群截面又被称为子群参数。
单个共振核在共振能区的多区慢化方程为:
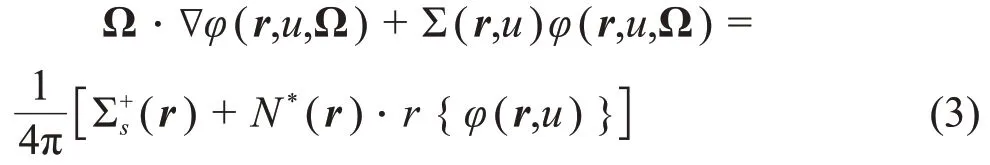
采用统计共振模型,结合子群定义式(2),共振核素的微观散射源可表示为:

将式(4)代入式(3),子群k的慢化方程可表示为:

式中:Σ+为非共振核素的宏观总截面;Σk为共振核素子群k的总截面为共振核素子群l的微观散射截面。
可通过迭代求解式(5)内子群通量,然后通过并群均匀化得到有效截面:
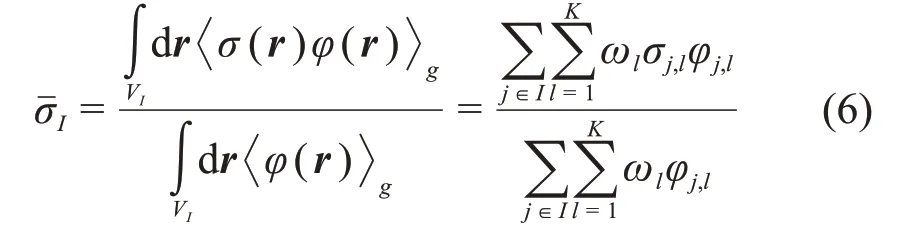
这套方法的前提条件是确定式(4)中子群参数,并期望它们与背景截面无关,从而能适用于不同的几何模型。考虑无限均匀介质,式(5)可直接给出通量的表达式,将其代入式(6),可得到有效截面与背景截面的关系:

由多群数据库可得到共振核素位于无限均匀介质内在给定离散背景截面点的有效截面,基于上述离散表点可采用帕德近似拟合得到与背景截面无关的子群参数。在实际非均匀系统求解时,共振核素背景截面不需要显式求解,直接使用式(6)得到有效截面。
1.2 ESSM方法
根据等价理论构建均匀共振积分表时,在背景截面σe,g下NJOY求解的无限均匀介质的慢化方程为:

将式(4)中的统计共振模型代入式(3),并对能群g、立体角和体积进行积分,可得:
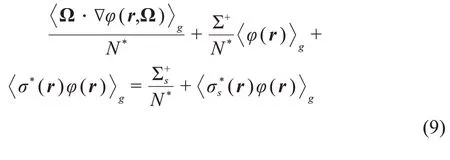
然后将式(8)右边共振核素的微观散射源同样采用统计共振模型。令式(8)和(9)等价,可得到背景截面σe,g的表达式:
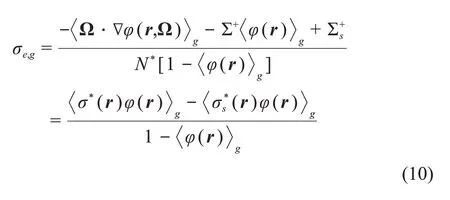
先假设通量、有效总截面及有效散射截面,通过式(3)得到该共振能群的通量φ(r)g,再通过式(10)得到背景截面,根据等价理论可插值得到新的有效总截面及散射截面,该过程迭代至通量收敛。
1.3 Tone方法
使用碰撞概率法表示式(3):

式中:Pij(u)为区域i产生的中子在区域j发生首次碰撞的概率。
共振核素的微观散射源采用式(4)中的统计共振模型,假设同一燃料区Gx内的任意平源区j和i的共振核素微观散射源相等[9]:
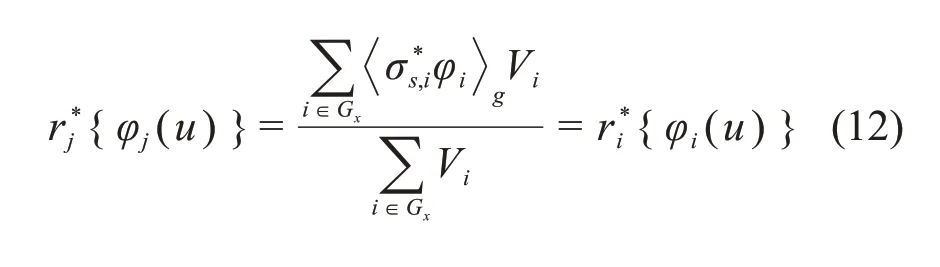
把式(12)代入式(11),并利用碰撞概率的互易关系,可得:
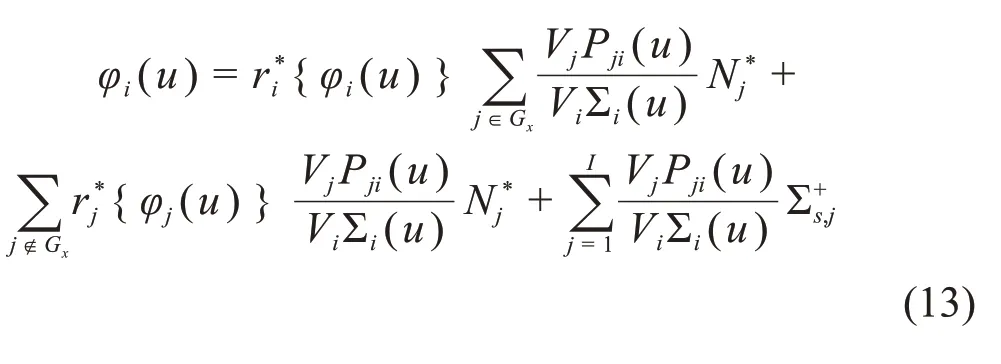
式(13)右边第二项表示位于其他燃料区的该共振核素对于燃料区Gx的贡献。
Tone方法引入一个关键近似,即碰撞概率的精细能群相关性只与碰撞发生的目标平源区i相关,可表示为:
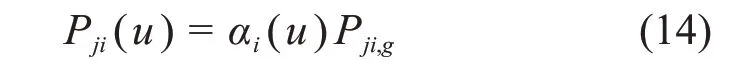
根据碰撞概率的互易性及守恒性,可推出该近似的精细能群相关系数的表达式,有:
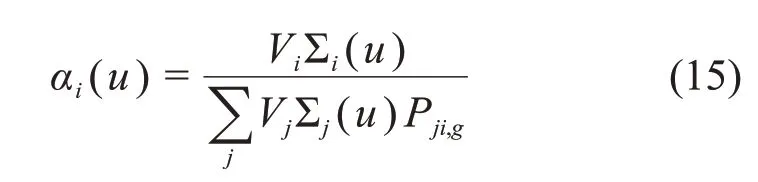
结合式(13)、(14)和(15),可得:

其中:

对比式(16)和(8),可知式(16)与构建均匀共振积分表时NJOY通量求解器求解得到的通量表达式相似。
Tone方法采用均匀截面假设,即对于所有燃料区该共振核素的微观散射源和总微观截面都取为待求燃料区Gx的值,αi(u)与βi(u)即反映该假设的影响,采用该假设后αi(u)与βi(u)等于0,式(16)与(8)等价,结合碰撞概率的互易性,式(16)中背景截面可表示为:
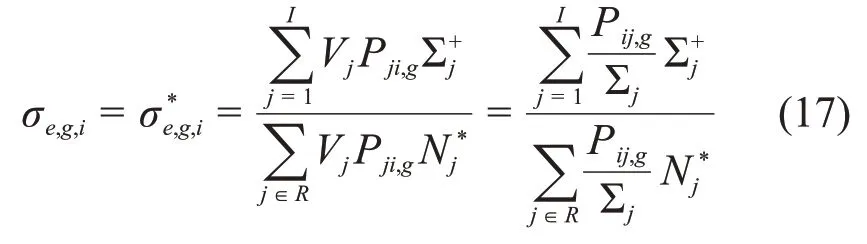
观察式(17),它的分子和分母与碰撞概率法的一般通量表达式相似(比如式(11)),因此可通过构造两个固定源输运方程将Tone方法推广到任意输运求解方法。这两个固定源输运方程可表示为:
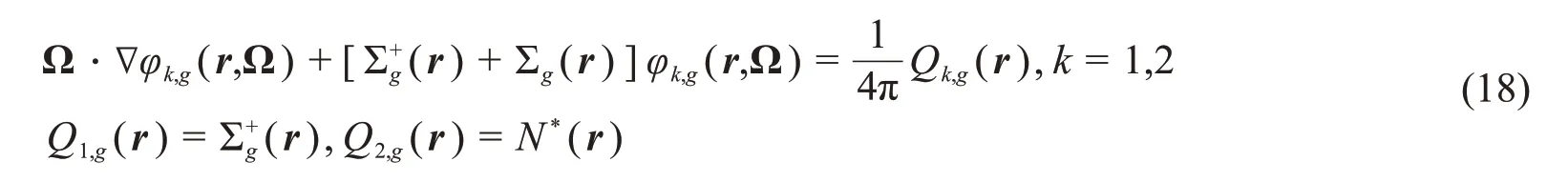
求解式(18)后,式(17)可表示为:

与ESSM类似,在式(19)得到背景截面后,通过均匀共振积分表插值得到有效总截面,然后再次求解式(18)更新背景截面,该过程迭代至通量收敛。
1.4 Tone-N方法
对于多燃料区,为评估不同燃料间的相互影响,避免Tone方法中均匀截面假设,本文提出了Tone-N方法。式(16)对能群g积分:

其中:
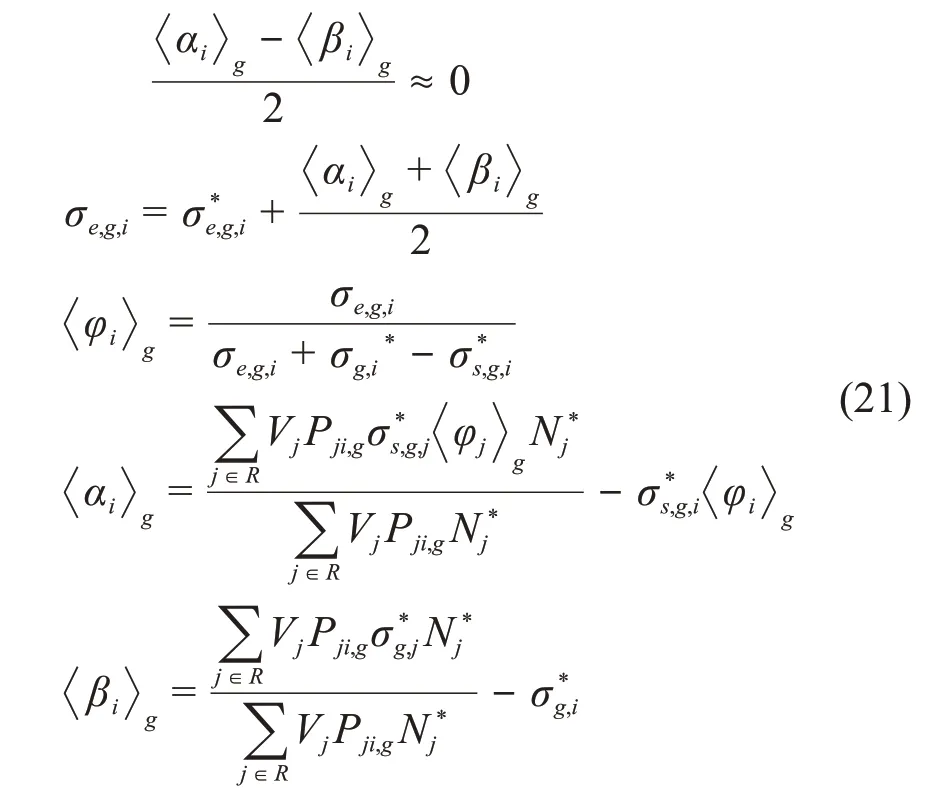
为求αi g和βi g,与(18)式类似,可额外引入两个固定源方程进行求解,这两个固定源方程的源项为:
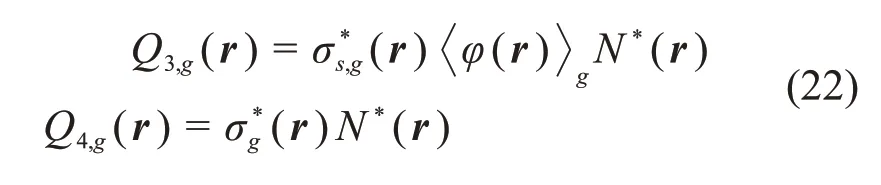
与式(19)类似,可用上述固定源方程求解的通量来表示αi g和βi g:
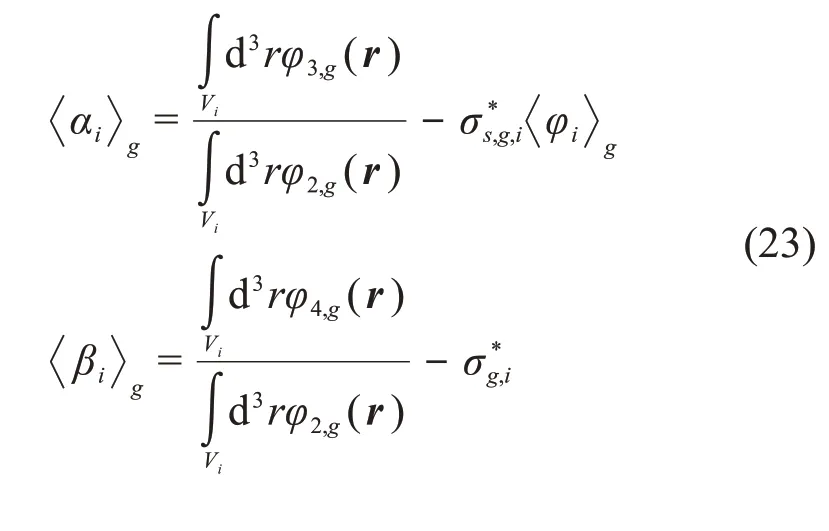
2 共振计算的实现
上述共振方法可归结到一套计算流程来实现。引入非共振核素的输运修正,上述共振方法可统一写成如下单共振核素慢化方程形式:


表1 子群法、ESSM、Tone和Tone-N在慢化方程上的差异Table 1 Difference in neutron slowing-down equations for different methods
式(24)的迭代求解流程如图1所示,并在ThorLAT[18]栅格程序中实现。首先从多群数据库中通过温度插值得到相应温度的各背景截面下的有效截面。子群法采用帕德近似拟合得到子群参数。然后,针对单共振核素假设进行所有共振核素的内迭代及外迭代循环。
式(24)求解时需要计算相关的系数矩阵,如果采用碰撞概率法,则计算碰撞概率矩阵;如果采用代数压缩加速方法(Algebraic Collapsing Acceleration,ACA)[18]的 源 项 孤 立 特 征 线 方 法(Method Of Characteristics,MOC),则计算ACA系数矩阵及自碰撞因子。由于子群截面是固定的,内迭代时子群法的系数矩阵只求解一次即可,而ESSM、Tone和Tone-N方法需要更新有效截面,系数矩阵需要不断更新,这增加了时间开销。由于Tone和Tone-N方法的多个固定源方程系数矩阵相同,只需要针对一个固定源方程求解。如果采用ACA加速的MOC方法,由于ACA加速是预处理的综合加速方法,可以不更新ACA系数矩阵,能节省时间且不影响计算精度。
求解慢化方程时,先假设初始通量,并取无限稀释截面为初始有效截面,通过表1中的源项表达式计算相应源项,然后求解式(24)来更新通量。ESSM或Tone方法分别采用式(10)或式(19)计算背景截面,Tone-N方法采用式(21)和式(23)计算背景截面,通过插值更新相应的有效总截面或散射截面。该内迭代过程直至式(24)求解的通量收敛。式(24)求解时所有共振能群统一求解,能有效减少MOC方法读取特征线的次数,提高求解效率。
本文中燃料区由不同的材料号区分,每个材料会指定相应温度。在ESSM、Tone和Tone-N方法中,温度分布直接对应到材料的温度,每个燃料区将使用温度相关的共振积分表来插值计算有效截面,从而近似考虑温度分布的影响。在子群法中,由于不同温度下共振核素的子群参数并不相同,所有温度点不能同时求解。一种方式是把不同温度点当成不同的共振核素,按式(24)的单共振核素假设来迭代计算处理,即所谓的不相关模型;另一种方式是采用全相关模型[5],即引入一个所有温度点的循环(如图1所示),在求解当前温度点核素时,其他温度点的核素都使用当前温度点的子群参数,但源项保留自身的散射源,该散射源可来自上次外迭代计算。全相关模型即求解如下慢化方程:
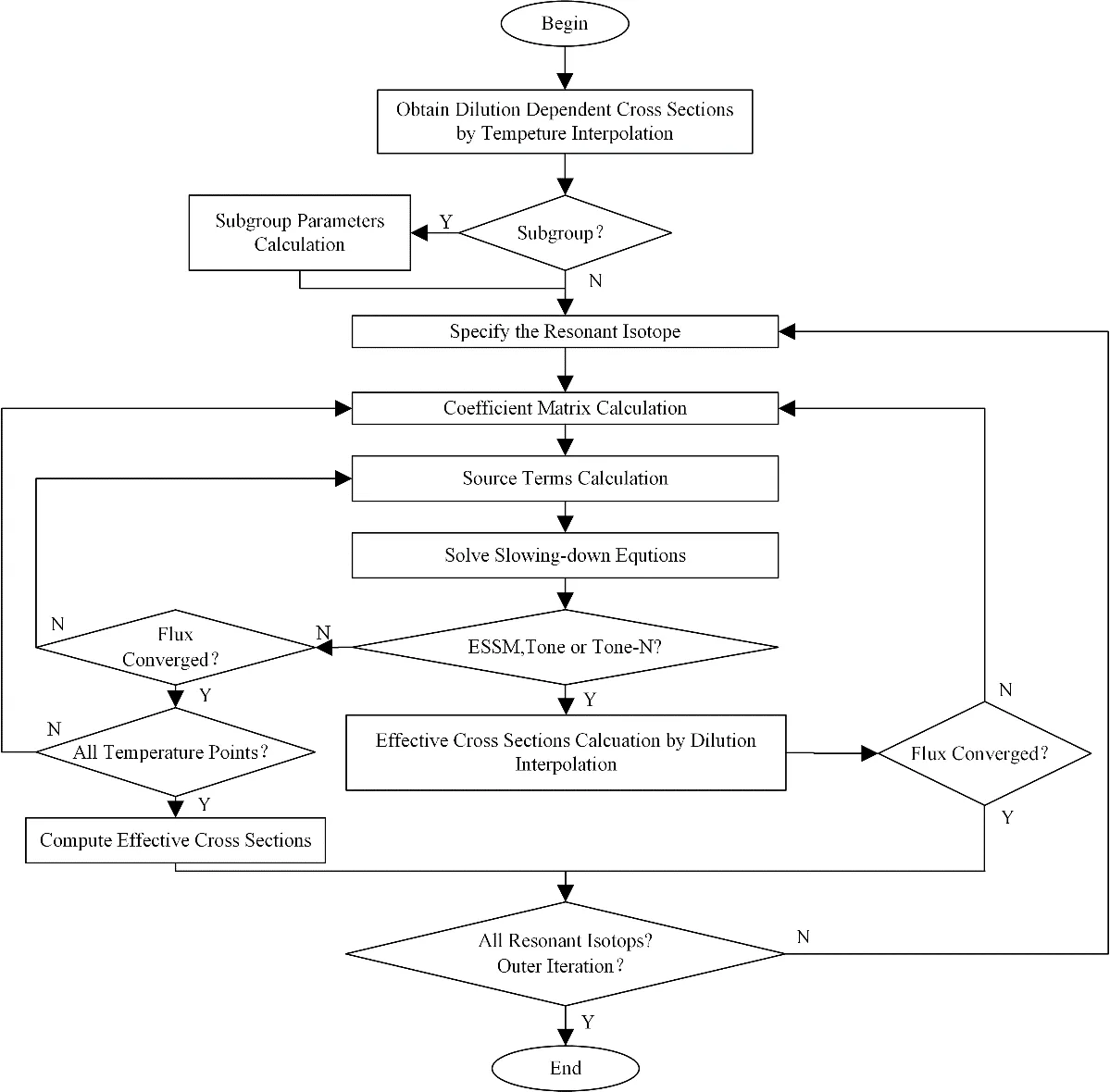
图1 实现Subgroup、ESSM、Tone和Tone-N方法的集成计算流程Fig.1 Integrated calculation process for implementation of subgroup,ESSM,Tone and Tone-N methods
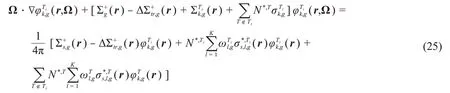
不相关模型和全相关模型的计算量是相同的,都增加了温度点迭代,会比ESSM或Tone方法更加耗时。
3 数值验证
3.1 VERA组件基准题
本文选取部分VERA组件基准题[19]对ThorLAT中不同共振计算方法进行验证,包括1/8 VERA-2A、VERA-2F、VERA-4A-2D、1/8 VERA-4B-2D以及1/8 VERA-4C-2D,其中VERA-2为17×17燃料棒组成的单组件模型,而VERA-4-2D为3×3组件组合模型。基准题参考结果数据来自文献[19]。所选基准题包括可燃毒物、AIC控制棒和B4C控制棒模型,能更全面验证共振计算方法的正确性,并覆盖不同求解规模来分析各共振计算方法效率。所有模型采用12线程并行计算,计算平台CPU为2.20 GHz的Intel至强银牌4214。微观截面库选用由ENDF/B-VII.1加工的SHEM361能群结构的Draglib数据库[20]。求解时设定极角数为4,方位角数为64,特征线间距为0.025 cm,采用材料网格代数归并加速方法(Material-Mesh Algebraic Collapsing Acceleration,MMACA)[18]加速MOC源迭代。Subgroup方法在子群并群均匀化时采用SPH因子修正。
表2列出了ThorLAT中不同共振计算方法对VERA基准题的计算结果。由表中数据可知,三种共振计算方法的keff及棒功率分布与基准题的SCALE参考解符合较好,最大keff偏差为223×10-5,出现在子群法计算AIG控制棒插入的VERA-4B-2D模型,最大功率偏差出现在B4C控制棒插入的VERA-4C-2D模型,约为2%,三种共振计算方法精度相当。在求解效率方面,Tone方法与ESSM方法耗时接近,且明显优于子群法,共振计算时间降低约55%。
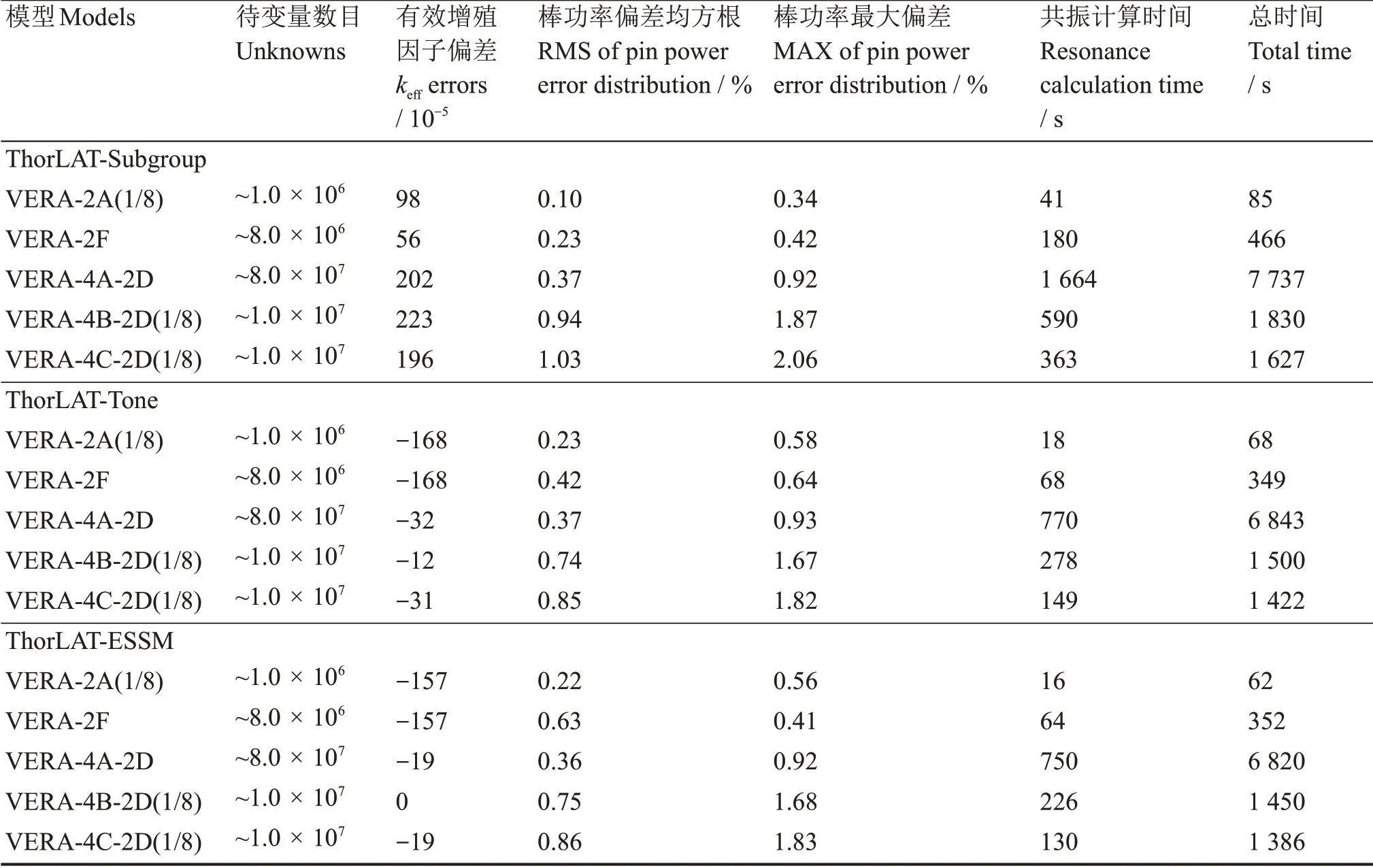
表2 ThorLAT中不同共振计算方法对VERA基准题计算结果Table 2 Results of VERA benchmark problems by using different resonance calculation methods in ThorLAT
3.2 通道式熔盐堆燃料栅元
以通道式熔盐堆的燃料栅元为对象,计算了三个算例:均匀温度的单燃料区、均匀温度的10燃料区和带温度分布的10燃料区,如图2所示。燃料栅元中熔盐通道半径为2 cm,对边距为10 cm。材料成分如表3所示。计算时忽略了温度对材料密度的影响。均匀温度算例的温度设定为900 K。如图2所示,三个算例具有相同等体积划分的平源区。参考解来自蒙特卡罗程序OpenMC[21]计算。ThorLAT和OpenMC使用的数据库都来源于ENDF/BVIII.0。
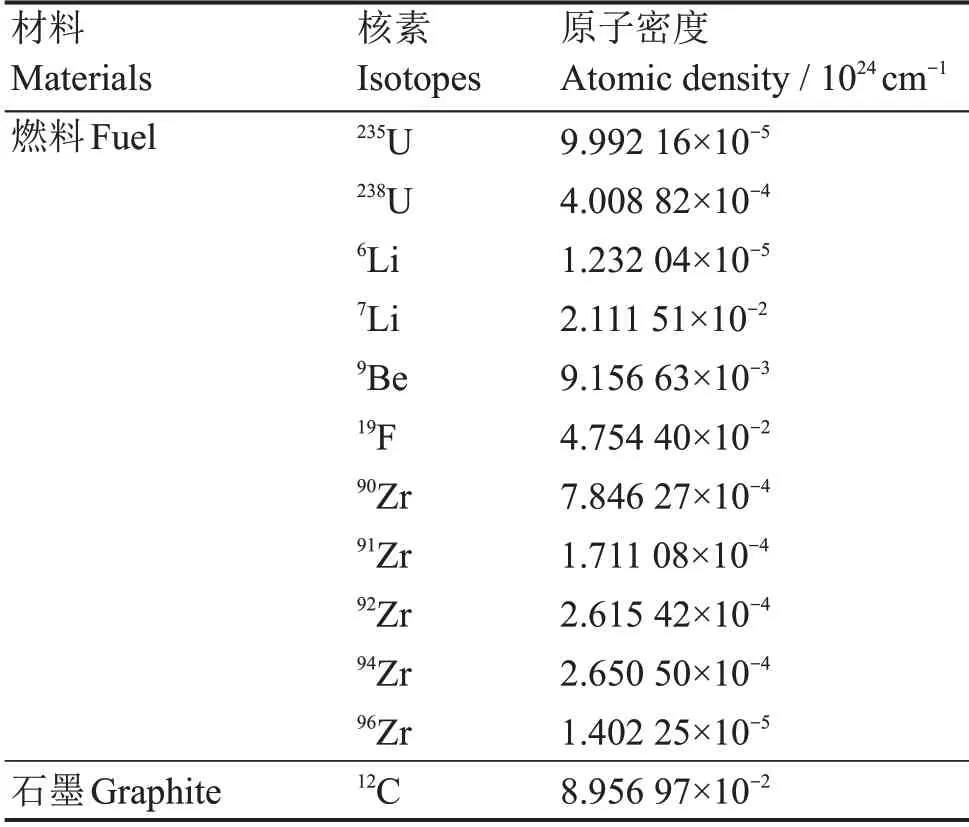
表3 通道式熔盐堆燃料栅元各材料的核素原子密度Table 3 Nuclide atomic densities of the materials in the fuel lattice of the channel-type MSR

图2 通道式熔盐堆燃料栅元计算模型Fig.2 Models for the fuel lattice of a channel-type MSR
3.2.1 Subgroup、ESSM和Tone共振计算法对比
不同共振方法计算得到的燃料区均匀化结果如表4所列,其中Subg1为不相关模型子群法,Subg2为全相关模型子群法。对于均匀温度算例,ThorLAT的计算结果与OpenMC参考解符合良好。最大keff偏差为1.80×10-3,U-238最大吸收截面偏差不超过3.35%,最大的U-238总吸收率偏差为1.84%。U-235最大吸收截面偏差较大,但U-235总吸收率偏差只有0.86%。与VERA基准题的结论相似,子群法、ESSM和Tone三个方法的计算精度相当。均匀温度的10燃料区算例的计算结果与均匀温度的单燃料区的非常接近,说明无温度分布下进一步增加燃料区对计算精度影响有限。图3具体给出了均匀温度的10燃料区算例中各燃料区及各共振能群的U-238吸收率偏差分布。ESSM和Tone方法的偏差分布相似,进一步体现两种方法精度相当。在30 eV的U-238共振峰处,两种方法会高估燃料区内部反应率,而子群法计算更准确,但从表4可知,该共振峰处偏差对总吸收率的影响较小。
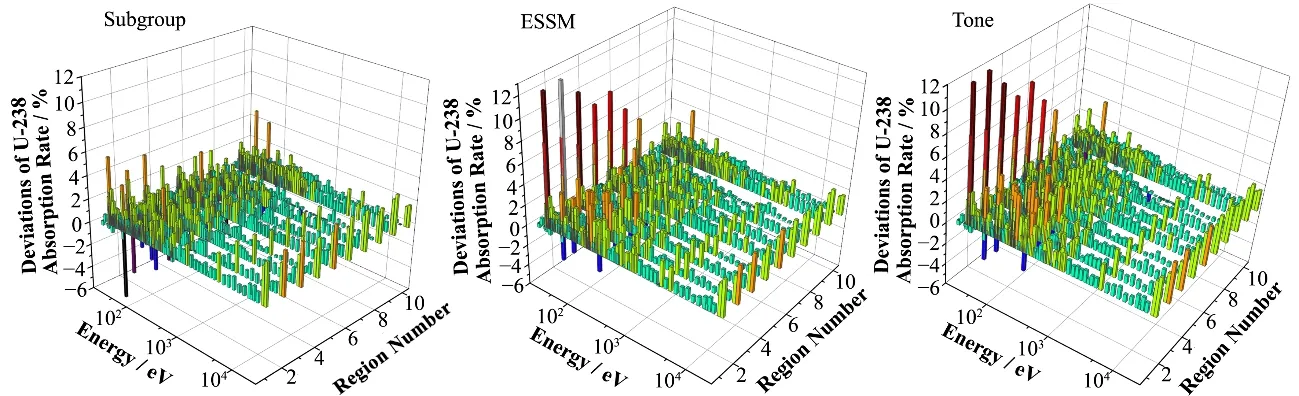
图3 均匀温度的10燃料区算例中U-238吸收率偏差分布Fig.3 Error distributions of U-238 absorption rates for case with 10 fuel zones and the uniform temperature distribution
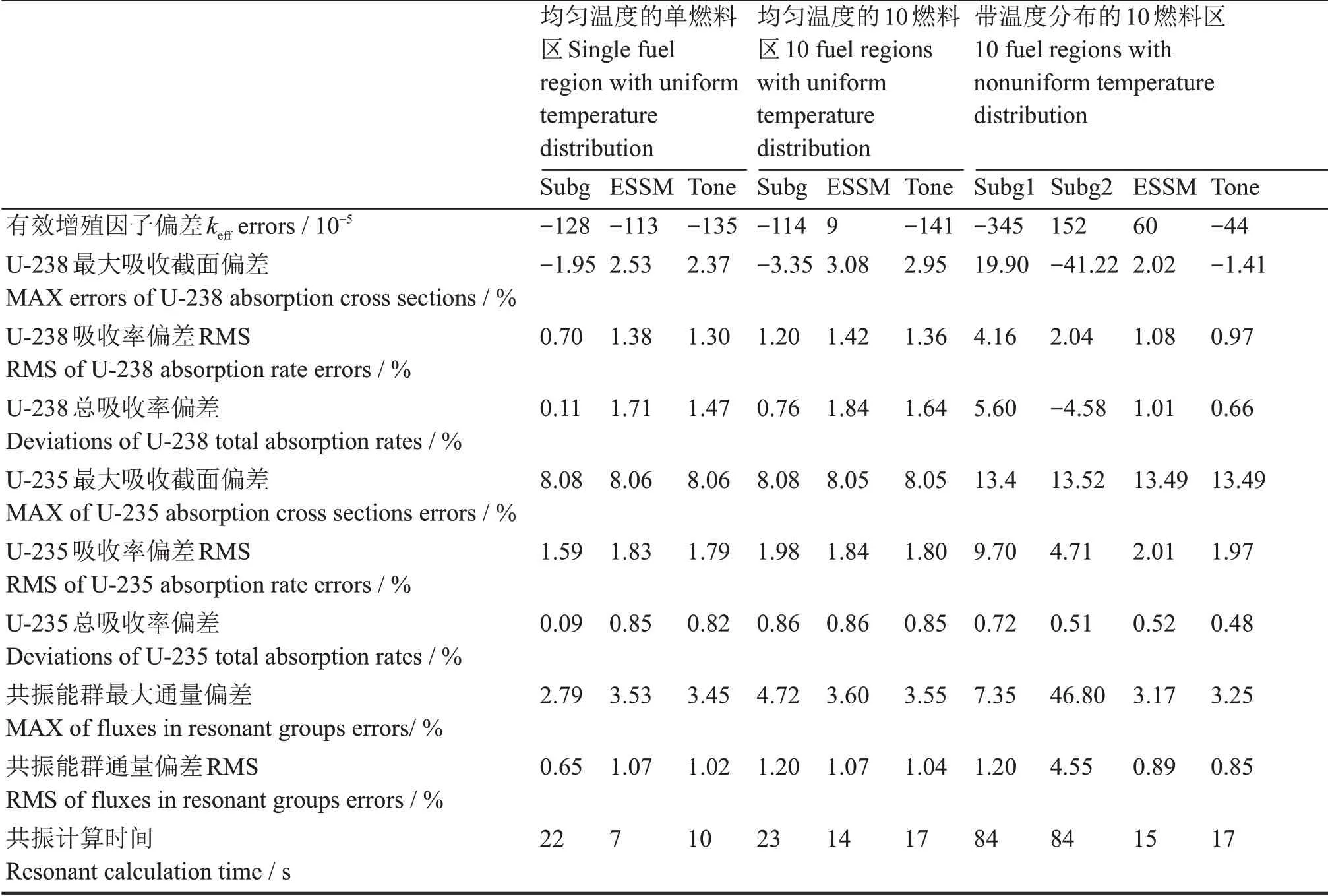
表4 不同共振方法计算得到的燃料区均匀化结果对比Table 4 Fuel zone homogenized results for different methods
当燃料区存在温度分布时,子群法的精度要低于ESSM和Tone方法。全相关模型子群法中U-238的最大吸收截面偏差及共振能群最大通量偏差较大,超过了40%。不相关模型的子群法中U-238总吸收率偏高5.60%,导致keff偏低了3.45×10-3。ESSM和Tone方法计算结果相似,U-238最大吸收截面偏差分别为2.02%和1.35%,U-238总吸收率偏差分别为1.01%和0.87%,U-235总吸收率偏差分别为0.52%和0.51%,这说明基于等价理论的ESSM和Tone方法能较好地处理温度分布下共振计算。图4给出了详细的带温度分布的10燃料区算例下U-238吸收率偏差分布。ESSM方法在低能段共振区稍优于Tone方法,但表4中结果表明总体上两种方法计算精度相似。采用不相关模型的子群法会明显高估低能段U-238的吸收率,而采用全相关模型的子群法会严重低估低能区相关共振峰处(36.8 eV、66.2 eV、103.0 eV和190.2 eV)的U-238吸收率,特别是燃料区内部区域,从而影响子群法处理温度分布问题的计算精度。
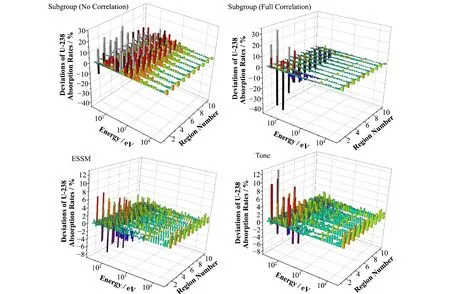
图4 带温度分布的10燃料区带算例中U-238吸收率偏差分布Fig.4 Error distributions of U-238 absorption rates for case with 10 fuel zones and the nonuniform temperature distribution
表4列出三种共振计算方法的计算时间。ESSM和Tone方法计算时间接近,且明显少于子群法的计算时间。图5给出了这三种方法每个共振能群的方程数及内迭代求解次数。子群法方程数最多且迭代次数最多,因此计算耗时最长。Tone方法方程数比ESSM的多一倍,但它迭代次数最小,所以它的计算时间与ESSM接近。由图5可知Tone方法具有最优的迭代稳定性。均匀温度的10燃料区算例中,需要进行插值的燃料区数增加了10倍,导致ESSM和Tone方法的计算时间增加。当存在温度分布时,子群法需要引入温度点循环,而ESSM和Tone方法计算时间基本不变,体现了ESSM和Tone方法在处理温度分布共振计算时显著的效率优势。
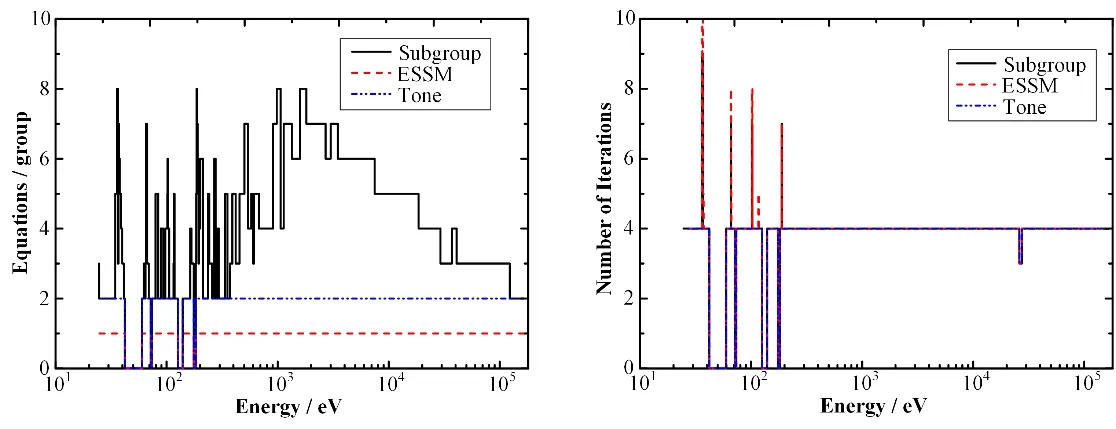
图5 不同共振方法的各共振能群方程数及内迭代求解次数Fig.5 Number of equations and iterations in each resonant group for different methods
3.2.2 Tone-N与Tone结果对比
表5列出了Tone-N方法对通道式熔盐堆的燃料栅元算例的计算结果。与表4中Tone方法计算结果对比,无论是否有多燃料区存在,Tone-N方法得到的结果与Tone方法的基本一致,Tone-N方法求解的方程数是Tone方法的两倍,因而计算更耗时。图6给出了带温度分布算例中Tone-N计算的U-238微观吸收截面与Tone方法的相对偏差,两者的结果只在低能段几个共振峰处有较小偏差。由于空间自屏效应,内部区域的截面低于外部区域,Tone-N方法避免了均匀截面假设,内部区域计算时会考虑外部区域更大截面的影响,将得到更大的背景截面,使得计算的吸收截面比Tone方法高。同理,Tone-N计算的外部区域截面比Tone方法偏低。以上结果说明Tone方法中均匀截面假设影响较小,验证了该假设的合理性。

图6 在带温度分布算例中Tone-N计算的U-238微观吸收截面与Tone方法的偏差Fig.6 Deviations of U-238 absorption cross sections calculated by using Tone-N and Tone’s method for the case with 10 fuel zones and the nonuniform temperature distribution

表5 Tone-N方法计算得到的燃料区均匀化结果Table 5 Fuel zone homogenized results obtained with the Tone-N methods
3.2.3 XMAS172和SHEM361计算结果比较
为评估较少能群下各类共振方法的计算精度,选取开源XMAS172能群结构的Draglib数据库,并对带温度分布的10燃料区算例进行了计算,结果如表6所示。全相关模型子群法相比于其它方法精度较高,特别是keff和U-238总吸收率偏差。ESSM、Tone或Tone-N在172群下偏差较大,keff偏差达到5.00×10-3以上,U-238最大吸收截面偏差达到9%左右。
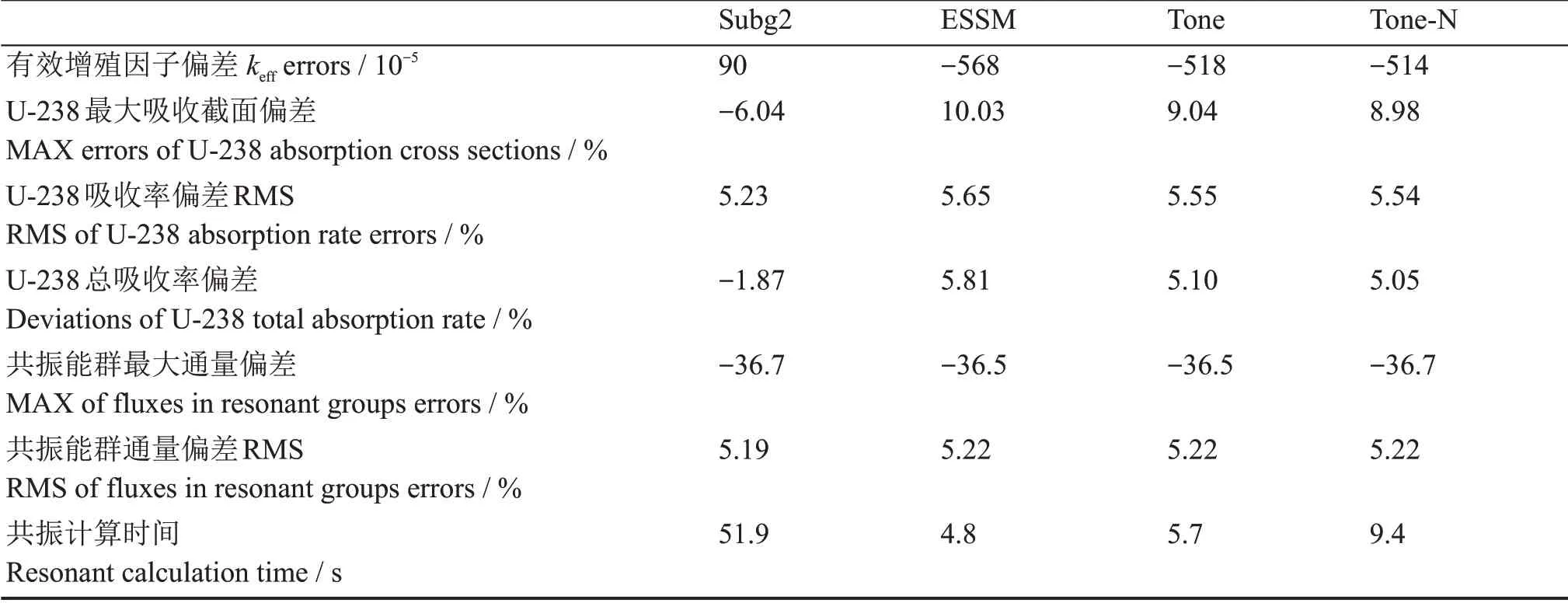
表6 XMAS172能群结构下带温度分布的10燃料区算例的燃料区均匀化计算结果对比Table 6 Fuel-zone homogenized Results in the XMAS172 energy group structure for the case with 10 fuel zones and nonuniform temperature distribution
为进一步说明增加能群数对计算精度的影响,以Tone方法为例,对比了两种能群结构下最内圈U-238吸收截面偏差分布,如图7所示。采用SHEM361能群结构的计算结果明显优于采用XMAS172能群结构的结果。下面分三个能段进行讨论:
1)22.5 eV以 下 能 区。6.2~7.5 eV和19.5~22.6 eV这两个共振能群的U-238吸收率占共振能区总吸收率60%左右,采用XMAS172能群结构时这两群的计算偏差较大,严重影响计算精度,但在SHEM361能群结构中这两个能群由于采用能群细分不再属于共振能区,这能有效处理该能段内空间自屏、不同共振核素或同一共振核素不同温度下共振峰间干涉效应。
2)22.5 ~400.0 eV的可分辨共振区。SHEM361能群结构下Tone方法对于能谱缓慢变化能区结果符合较好,但对于能谱畸变位置存在一定偏差。由于通量畸变处能群勒宽较小,这对总吸收率影响有限,进而对计算精度影响较小。Tone方法采用式(14)的近似来简化共振峰内精细谱的碰撞概率,进而得到与精细谱无关的背景截面表达式,导致求解背景截面时无法准确考虑精细谱的影响,造成XMAS172能群结构的结果偏差较大。为减少该近似带来的偏差,可通过增加能群数得到更逼近精细谱的能谱结构,比如采用SHEM361能群结构的计算结果。这也是采用XMAS172能群结构的子群法结果优于Tone方法的原因,因为子群法通过概率表方式能近似体现具有较大勒宽共振能群的能谱信息。
3)400.0 eV以上的共振能区。Tone方法在两种能群结构中都能给出较好结果。ESSM方法同样能得到图7类似结果。综上所述,在可分辨共振能区增加能群数可得到更逼近精细谱的能谱结构,从而有效改进ESSM和Tone方法的计算精度。

图7 带温度分布算例中最内圈计算结果(a)和(b)分别是采用XMAS172或SHEM361能群结构时Tone方法计算的U-238吸收截面偏差,(c)和(d)分别是OpenMC计算的针对XMAS172或SHEM361能群结构的共振能区归一化能谱Fig.7 The results of the inner-most region for the case with 10 fuel zones and nonuniform temperature distribution(a)and(b)are the deviations of the U-238 absorption cross sections obtained with the Tone's method under XMAS172 or SHEM361 energy group structures respectively,(c)and(d)are the normalized fluxes calculated by OpenMC under the two energy group structures respectively
4 结语
本文探讨适合于熔盐堆的共振计算方案。首先介绍了适用于复杂几何且不依赖Dancoff因子修正的子群法、ESSS、Tone和Tone-N共振计算方法理论,其中Tone-N方法是通过引入两个额外的固定源方程来考虑多燃料区间相互影响的一种新方法。然后对这些方法的通用单共振核素慢化方程形式进行了总结,设计了统一的计算流程,并在ThorLAT栅格计算程序中实现了该统一计算流程。采用SHEM361能群结构,先通过VERA组件基准题验证ThorLAT中共振计算方法实现的正确性,然后针对均匀温度或存在径向温度分布的通道式熔盐堆燃料栅元进行了计算及分析。
VERA组件基准题中keff及棒功率分布与参考解符合良好,说明了方法实现的正确性。子群法、ESSM和Tone方法对于VERA基准题的计算精度相当,但ESSM和Tone方法计算效率比子群法提升1倍以上。
对于均匀温度或存在径向温度分布的通道式熔盐堆燃料栅元计算表明:1)ESSM和Tone方法计算的keff偏差在1.50×10-3以内,最大燃料区均匀化U-238吸收截面偏差低于3.1%,在带温度分布算例中这两种方法计算结果比不相关模型或全相关模型的子群法精度高且具有显著的效率优势;2)与ESSM方法相比,Tone方法具有更稳定的迭代收敛;3)Tone-N方法的计算结果与Tone方法基本相同,说明了Tone方法中均匀截面假设的合理性;4)与XMAS172能群结构的结果对比表明,在可分辨共振能区增加能群数可得到更逼近精细谱的能谱结构,从而有效改进精度。
综上所述,通过熔盐堆燃料栅元模型的计算,本文初步验证了SHEM361能群结构下基于均匀共振积分表插值的ESSM和Tone方法对于熔盐堆共振计算的适用性。
作者贡献声明戴明:负责本论文方案设计,程序开发,数据整理分析,论文撰写和修改;张奥:负责基准题参考解计算及结果数据整理,论文修改及校订;程懋松:参与方案设计,对文章的知识性内容作批评性审阅,论文修改。

