基于障碍物可达区域预测的机器人实时避障算法

彭 帆， 谢永芳， 陈晓方， 殷泽阳

(中南大学 自动化学院， 湖南 长沙 410083)

自主移动机器人因具有价格便宜、操作灵活、运动范围广等优势，在电力领域和安防领域得到了成功应用，在铝电解和浮选等流程工业领域的巡检任务中有着巨大的应用潜力.未来移动机器人的研究趋势是智能化和自主化，安全实时避障是提高移动机器人自主规划能力的关键技术之一.巡检任务中机器人所处的工厂环境复杂，如存在操作工人、大型静态障碍物等，对工业巡检移动机器人的自主避障能力提出了更高要求.随着我国向工业4.0和制造强国2025的迈进，复杂多变的工业环境与巡检移动机器人自主规划能力不足之间的矛盾日渐凸显，制约我国工业巡检机器人向自主化、智能化发展的问题之一.

现有的移动机器人避障方法主要分为以下5类：基于图论的方法、基于群智能的启发式算法、随机规划法、基于预测的算法、基于实时状态势场函数法等混合方法.图论方法包括A*算法[1]、维诺图法[2]、PRM算法[3]等，该类方法融合贪心算法和启发函数的思想，通过遍历查询的方式寻找从起点到目标点的可行路径，但所得路径并非最优，且遇到动态障碍物时需要重新规划路径.基于群智能的启发式算法包括粒子群法[4]、遗传算法[5]、蚁群算法[6]等，这类算法具有实现容易、精度高、鲁棒性好的优点，但需要耗费大量计算资源，难以保证复杂环境下规划的实时性.随机规划法包括RRT[7]、RRT*[8]及Bi-RRT等，这类方法构造简单并能够较快搜索未知空间，但其得到的避障路径随机性太强，且在避障路径上存在曲率不连续的点，难以保证避障轨迹的平滑性.障碍预测算法[9]在预测障碍物未来的运动轨迹的集合基础上，通过优化指标函数寻求避障路径.障碍预测算法提高了机器人对障碍物的预测能力，但需要在每一个迭代步求解优化问题，对控制器的实时性提出了较高要求.基于实时状态的势场函数法数学运算快、易于实现且实时性较好，所得路径平滑、跟随性能较好.文献[10]考虑机器人的性能约束，构建离散化的可行集合，进而选取最低势场点作为机器人的下一位置，能够有效减轻计算负担.实时势场函数法一般将静态障碍和动态障碍统一处理，没有考虑动态障碍物的运动趋势.

受基于障碍预测算法和基于实时状态的势场函数法的启发，提出一种基于障碍物可达区域预测的移动机器人实时避障算法.相比于传统的人工势场法和动态窗口法，该方法的主要优势如下：①相比于人工势场法，通过快速给出动态障碍物预测时域内可达区域，考虑动态障碍物的运动趋势，可以提前确定机器人可行的避障区域并能够解决移动机器人路径绕远和躲闪不及问题，有效增强了机器人避障的安全性；②相比于动态窗口法，基于复合势场可以快速获得移动机器人的控制量，满足避障的实时性要求；③建立了基于可达区域预测的多步椭圆包络势场、基于新型Sigmoid函数的方形障碍势场和对数Lyapunov引力场等多种势场模型，使所提避障方法具有较好的地形适应特性与较高的避障能力.

1 机器人运动模型

移动机器人带有稳定的底盘控制系统，可实现偏航角及位置的跟踪控制.以大地坐标系x0y为基准进行机器人的运动描述，如图1所示.三自由度运动模型为

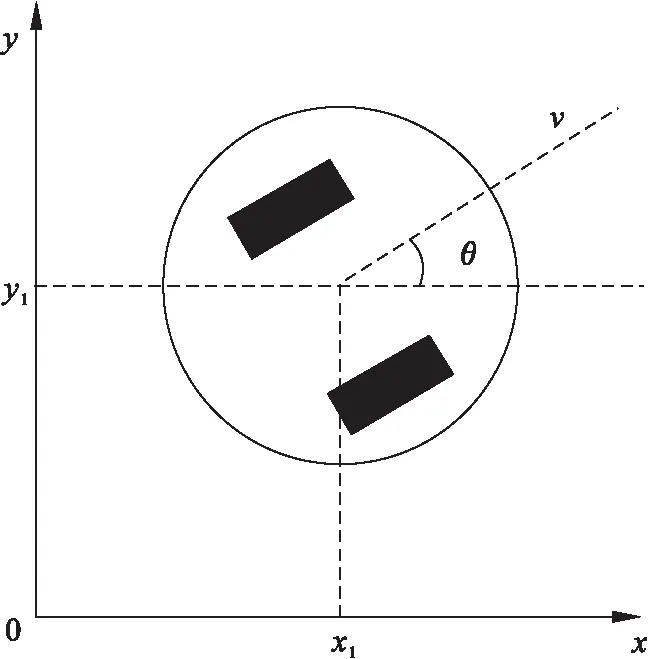
图1 移动机器人及大地坐标系x0y示意图Fig.1 Schematic diagram of mobile robots and earth coordinates

(1)

式中：q=[x1,y1]T为大地坐标系下移动机器人的位置；av,ωθ表示控制输入；v,θ为移动速度和行驶角；v=[vcosθ,vsinθ]T为移动机器人的速度矢量.

移动机器人状态和控制输入应满足以下约束条件以确保避障路径的平滑性和执行机构的可行性：

(2)

采用工程常用的比例积分反馈与前馈控制来确定各控制输入：

(3)

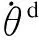
(4)

式(4)的行驶角误差和行驶速率误差都能以指数形式迅速收敛到零.重点研究如何设计实时避障算法得到期望速度矢量vd=[vdcosθ,vdsinθ]T和期望行驶角θd.

2 障碍物建模

2.1 静态障碍物建模

智能工厂中移动机器人的行驶区域中存在多种类型的障碍物，激光雷达等传感器感知到的信息还不够全面，如果过分关注工厂的环境信息，将降低算法的计算效率，对避障效果提升不大，因此综合考虑障碍物建模精确度及硬件的计算能力，将静态障碍物用圆形区域或方形区域包络.

1) 方形障碍物：将方形障碍物定义为中心位置(xr,yr)，边长为lr1,lr2的矩形，则可以定义关于坐标(x,y)的函数hr(x,y)为

(5)

当hr(x,y)>0,hr(x,y)=0,hr(x,y)<0时，分别表示方形障碍物外部区域、表面区域及内部区域.

2) 圆形障碍物：圆形障碍物定义为中心位置(xc,yc)，半径为rc的圆形，则可以定义关于坐标(x,y)的函数hc(x,y)为

(6)

当hc(x,y)>0,hc(x,y)=0,hc(x,y)<0时，分别表示圆形障碍物外部区域、表面区域及内部区域.

2.2 动态障碍物可达区域预测模型

智能工厂中存在多种动态障碍物，如操作工人、各类移动机器人等.为更有效地描述动态障碍物，以动态障碍的质心为圆心，在某一时刻用半径rc的圆形包络表示动态障碍物当前区域，并假设动态障碍物的运动速度在有限的预测时域内为恒定，其当前测量值带有不确定的高斯噪声.

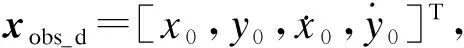
(7)

式中：

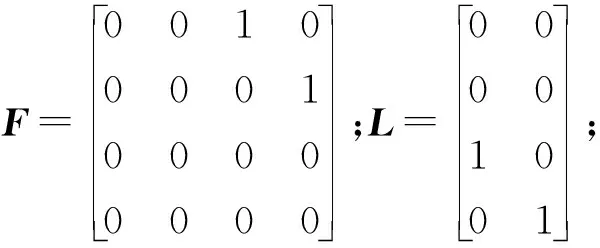
μ(t)～N1(0,q1)表示障碍物运动速度的不确定性，其均值为0；方差为q1=[m1,m2]T；τ(t)～N2(0,q2)为传感器量测噪声，其均值为0，方差为q2=[n1,n2]T.

对式(7)进行离散化，则其每个时间步长的状态更新方程为

xobs_d(k+1)=Axobs_d(k)+ωs(k) ,

(8)

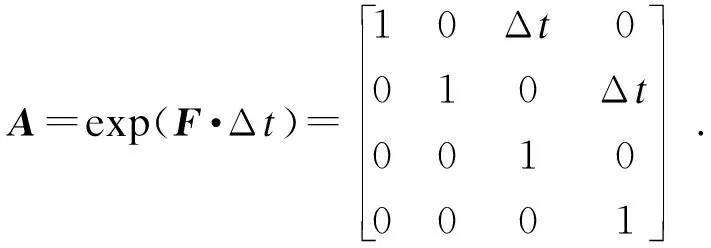
(9)

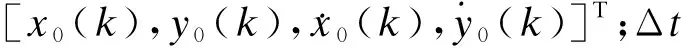
(10)

2) 动态障碍物可达区域预测：传统的人工势场法和动态窗口法可用于实时避障任务，但需要预先给定算法参数.由于移动机器人在智能工厂中的环境是动态变化的，仅依赖固定算法参数，而忽略当前或未来的运动趋势，常常会因为机器人动力学性能的限制而导致移动躲避动态障碍物不及时，或出现路径绕远的问题.因此需要对移动机器人的实时避障任务作出实时优化和调整.

为解决上述问题，提出动态障碍物可达区域预测算法，通过充分考虑动态障碍物未来运动趋势并留足裕量，提前确定动态障碍物的可达区域.基于式(8)建立动态障碍物的状态更新方程，并依据实时探测障碍物信息预测未来的运动状态.设定预测时域Th=pΔt，其中p为正整数，基于最优预测理论构造出关于预测时域Th=pΔt的p步预测方差公式，求得预测步数p的动态障碍物质心的可达区域.

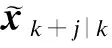
(11)

(12)

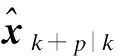
(13)

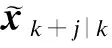
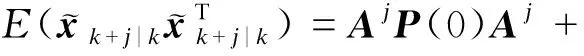
(14)

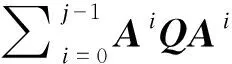
(15)

由式(14)可得动态障碍物质心在水平方向的方差σ1和垂直运动方向上的方差σ2，则其质心的可达区域可用(x0(k),y0(k))为中心，长轴为3σ2，短轴为3σ1的椭圆来表示.

基于上述分析，提出动态障碍物可达区域预测算法如表1中算法1所示.以预测时域Th=4Δt为例，基于动态障碍物可达区域预测算法求得的质心可达区域如图2所示.

表1 动态障碍物可达区域预测算法Table 1 Reachable area prediction algorithm of dynamic obstacle

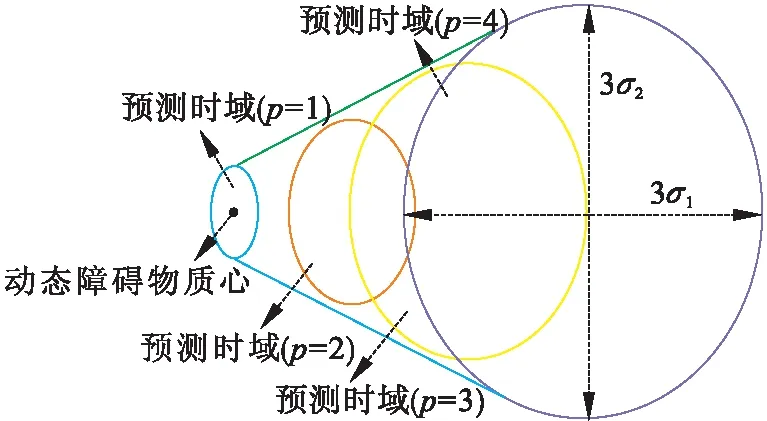
图2 预测时域Th=4Δt动态障碍物质心可达区域示意图Fig.2 Illustration of the predicted reachable area of dynamic obstacle in time horizon Th=4Δt

3 机器人实时避障算法

基于静态障碍物模型与动态障碍物可达区域预测模型提出机器人实时避障算法.

3.1 对数Lyapunov引力场模型

为引导移动机器人最终到达目标点qd(xd,yd)，定义关于目标的引力场对数Lyapunov距离函数为

(16)

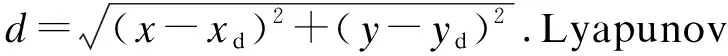
(17)

引力函数为

(18)

上述对数Lyapunov引力场引导移动机器人在无障碍空间下沿引力梯度到达目标点.

3.2 基于动态障碍物可达区域预测的多步椭圆包络势场模型

基于动态障碍物可达区域预测算法求得预测时域Th=pΔt内动态障碍质心可达区域的基础上，考虑动态障碍物具有一定的几何尺寸，将可达区域外扩障碍物半径r1，然后基于动态障碍物可达区域预测构建包络势场.

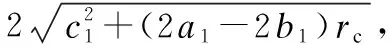
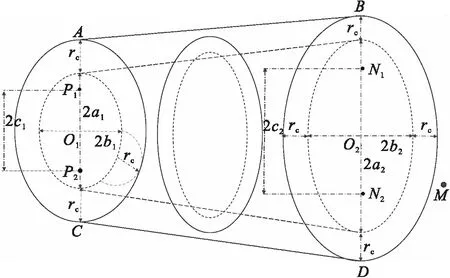
图3 预测时域Th=3Δt椭圆包络动态障碍物可达区域Fig.3 The reachable area of a circular envelope dynamic obstacle in the prediction time horizon

对于空间中任意一点M(x,y)，多步椭圆包络势场为

(19)

(20)

式中：d1=|2(a1+rc)-‖MN1-‖MN2‖|；UN(M)和UAB(M)分别为椭圆N1N2和直线AB部分产生的势场；‖MN1‖是机器人到焦点N1的距离；‖MN2‖是机器人到焦点N2的距离；d0,d2分别表示动态障碍物势场的影响距离和空间中一点到AB之间的距离；kf和kAB分别是椭圆N1N2和直线AB的影响系数.同理可得，动态障碍物的多步包络椭圆势场表达式和示意图如式(21)和图4所示.

图4 基于动态障碍物可达区域预测的多步椭圆包络势场Fig.4 Multi-step ellipse envelope potential field based on prediction of dynamic obstacle reachable area

U1=UN(M)+UP(M)+UAB(M)+UCD(M).

(21)

对式(19)和式(20)求负梯度可得斥力函数：

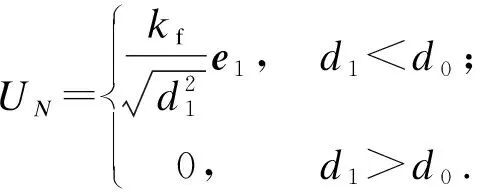
(22)

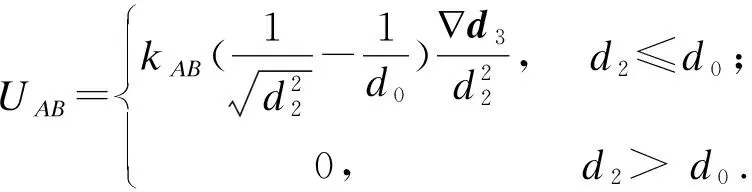
(23)

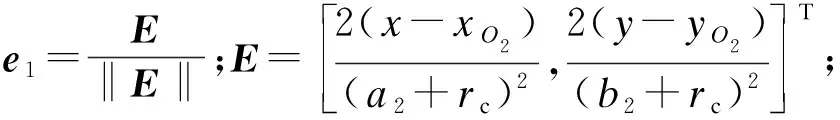
∇d3=[sinψ-sinλ*,cosλ*-cosψ]T；O2为焦点N1和焦点N2的中点，记为O2(xO2,yO2)；椭圆N1N2的长轴为2a2,短轴为2b2；ψ和λ*分别表示点M(x,y)至AB两端的连线与AB形成的夹角.

同理可得动态障碍物多步椭圆包络势场的总斥力为

F1=-∇U1=[F1,F2]T.

(24)

3.3 基于新型Sigmoid函数的方形障碍物势场模型

移动机器人行驶过程中会遇到各类静态障碍物，在建立静态障碍物模型的基础上，构建基于新型Sigmoid函数的方形障碍物势场模型：

(25)

方形障碍物的斥力函数F2为斥力势能函数的负梯度：

F2(M)=-∇U2(M)=

(26)

式中：ri=[sinβi-sinαi,cosαi-cosβi]T；ki是新型Sigmoid函数的增益系数；r与方形障碍物的影响范围有关；Si表示方形障碍物的第i面的函数表达式[11]；hc(M)是方形障碍物函数表达式；αi和βi分别表示方形障碍物第i面上的两个端点分别与机器人位置之间的夹角；ri是方形障碍第i面上的方向向量，方向指向方形障碍物外侧.

3.4 圆形障碍物的势场模型

对于非方形的静态障碍物，基于圆形障碍物模型构建圆形障碍物势场：

U3(M)=

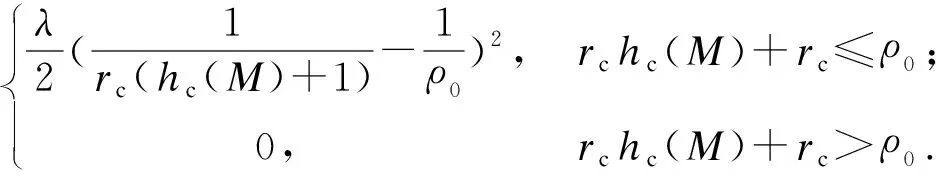
(27)

F3=-∇U3.

(28)

式中：ρ0为圆形障碍物的影响距离；λ为圆形障碍物势场系数；rc(hc(M)+1)为机器人质心到圆形障碍物中心的距离.

3.5 移动机器人实时避障算法

在多步椭圆包络势场斥力F1、新型Sigmoid函数的方形障碍物势场斥力F2、圆形障碍物的势场斥力F3、目标势场引力Fattr作用下，总势场力可定义为Ftotal=F1+F2+F3+Fattr=[Ftotal1,Ftotal2]T，机器人在上述综合势场的期望速度矢量vd=[v1,v2]T，期望行驶角θd可以通过求解方程组(29)来确定：

(29)

arctan(Ftotal)=

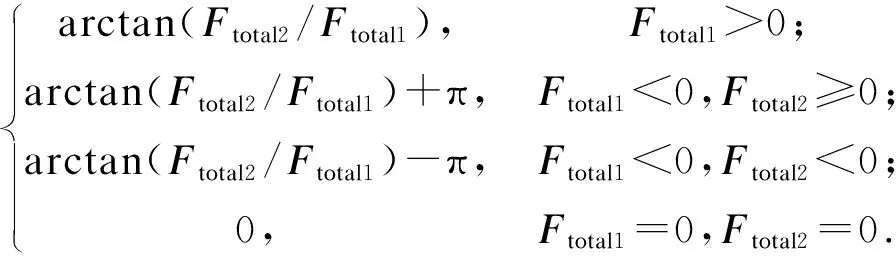
移动机器人在静态和动态障碍的混合空间下按式(30)和式(31)迭代到达目标点：

(30)

θ(t+1)=θ(t)+ωθΔt.

(31)

式中：[v1,v2]T，qd(t)，ω分别为移动机器人在大地坐标系下的速度，t时刻机器人的位置、角速度.

4 仿真分析

避障算法在动态障碍物上的避障能力的可靠性和复杂环境下对多种障碍物的安全避障能力进行仿真实验.设移动机器人行驶角θ∈(-0.523 5,0.523 5)rad，则最大行驶角变化为|Δθ|=|θmax-θmin|<1.047 rad，移动机器人的期望速度为恒定值vd=0.5 m/s.动态障碍物的预测步数p=4，预测时域Th=pΔt=4 s.

4.1 动态障碍物避障仿真

为了检验基于可达区域预测的多步椭圆包络势场在多动态障碍物的环境中进行实时路径规划的有效性，在仿真环境中随机生成5个动态障碍物：obs1，obs2，obs3，obs4和obs5.设定移动机器人从起点(25,70)m出发，向目标点(132,132)m运动，初始行驶角为30°，仿真结果如图5所示.

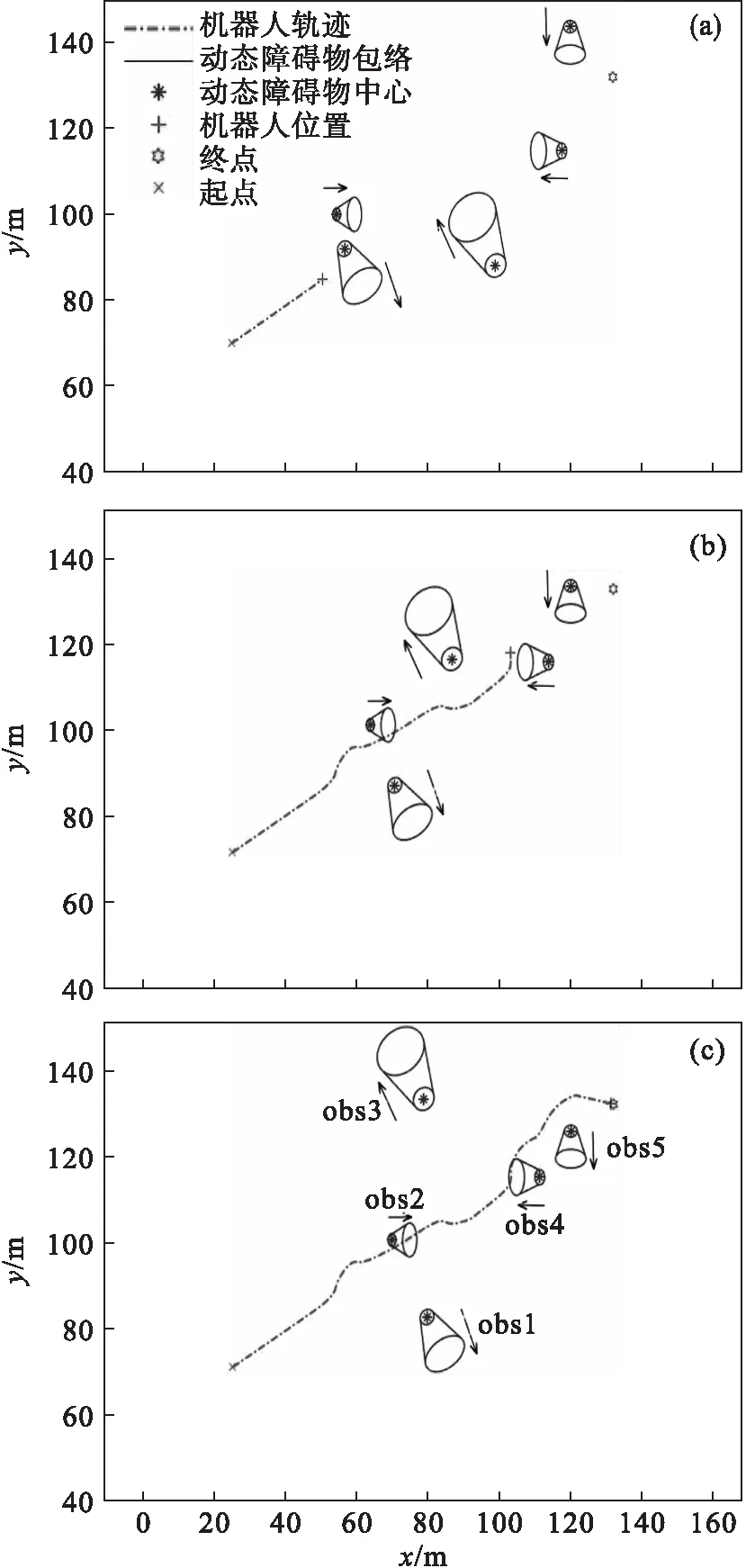
图5 多动态避障仿真结果Fig.5 Multi-dynamic obstacle avoidance simulation result(a)—t=75 s； (b)—t=240 s； (c)—t=330 s.

由图5可知基于动态障碍物的实时避障算法较好地解决了躲闪不及和路径绕远问题，既能实现局部路径规划、躲避多个动态障碍物，还能通过实时规划快速到达目标点，得到平滑且安全的路径.

4.2 多类型障碍物的复杂环境避障仿真

为了分析本文提出的移动机器人安全避障算法在多类型障碍物的混合环境中的可靠性，设定移动机器人从起点(10,10)m出发，向目标点(100,100)m运动，初始行驶角为45°.任务空间中随机生成2个动态障碍物obs6和obs7，以及4个圆形障碍物和2个方形障碍.

采用本文提出的基于可达区域预测的移动机器人实时避障算法和文献[12]中改进动态窗口算法的仿真结果如图6和图7所示.两种方法的结果对比如表2所示.采用基于可达区域预测的移动机器人实时避障算法时，机器人在进行局部安全避障的同时，解决了路径绕远和躲避障碍物不及时问题，且路径长度、最大线速度和最大行驶角变化都优于改进型动态窗口算法.两种算法下的平均线加速度和平均角加速度在改进动态窗口算法下均大于本文所提避障算法，这对移动机器人的电压驱动模块提出更高的性能要求，导致联接装置更容易发生磨损.因此，实时避障方法更为合理、实用.

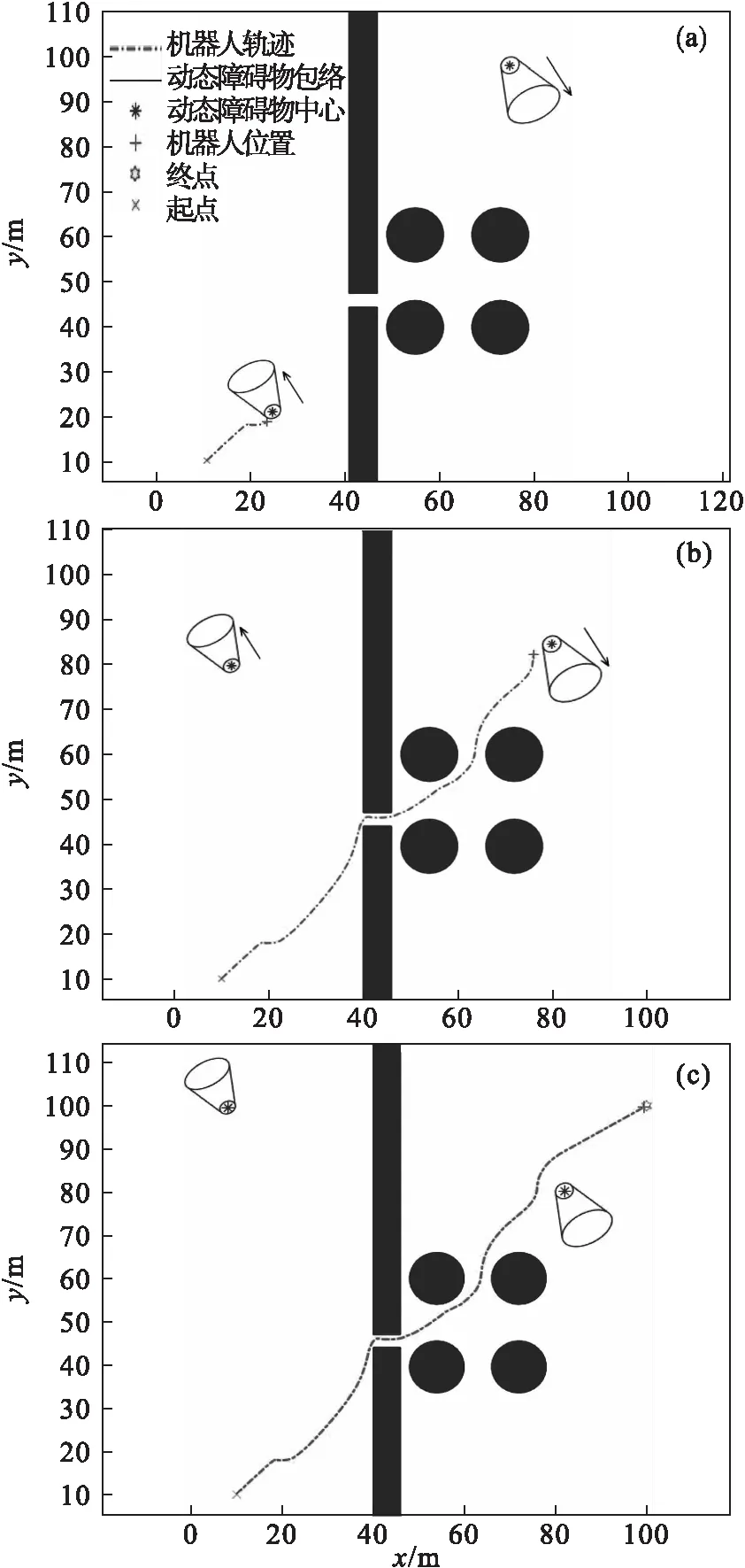
图6 混合复杂环境下基于障碍物可达区域预测的实时 避障仿真结果Fig.6 Simulation result of real-time obstacle avoidance algorithm based on obstacle reachable area prediction in a mixed complex environment(a)—t=55 s； (b)—t=350 s； (c)—全局规划轨迹.

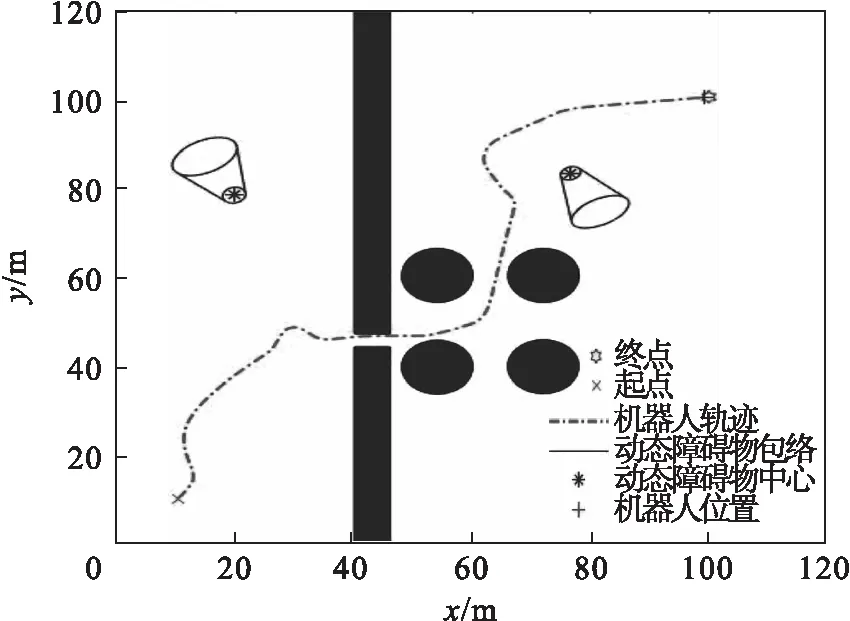
图7 混合复杂环境下改进动态窗口法避障仿真结果[12]Fig.7 Simulation results of improved dynamic window method for obstacle avoidance in mixed complex environment[12]

表2 基于障碍物可达区域预测的实时避障算法与改进动态窗口法算法结果对比Table 2 Comparison results of real-time obstacle avoidance algorithm based on obstacle reachable area prediction and improved dynamic window algorithm

5 实验验证

5.1 实验平台与实验环境介绍

使用团队自主研制的4轮独立驱动移动机器人样机进行实验验证.硬件配置包括嵌入式单片机控制器、4个100 W的直流电机、电机驱动模块、工业微型电脑.传感器配有二维激光雷达测距模块、3轴加速度计陀螺仪、轮式编码器，移动机器人实验样机如图8所示.移动机器人通过激光雷达采集环境信息，使用Gmapping算法建图定位并给定目标点，移动机器人底层控制器通过接受ROS操作系统中的避障算法下发速度命令控制机器人移动.

图8 移动机器人实验平台Fig.8 Mobile robot experimental platform

使用移动机器人模拟复杂工厂环境下的动态障碍物，并将小车以圆柱体包裹形成动态障碍物的圆形包络，以验证所提避障算法的可行性.动态障碍物演示验证平台如图9所示.

图9 动态障碍物演示验证平台Fig.9 Dynamic obstacle demonstration and verification platform

实验环境为宽5.2 m，长8 m的室内大厅，移动机器人的起始点坐标设为(2.4，0)m，起始行驶角为90°，目标点为(2.4，4.2)m.实验空间中存在单个动态障碍物，且动态障碍物的起点为(0，2.5)m，运动速度设定为0.2 m/s，运动方向为x轴正方向.

5.2 实验结果分析

采取传统的人工势场法(artificial potential field, APF)和基于动态障碍物可达区域预测模型的多步椭圆包络势场进行对比实验.令APF斥力函数的影响距离与多步椭圆包络势场的影响距离保持一致，多步椭圆包络势场形成的预测可达区域的面积应与传统的人工势场法中的圆形区域面积保持一致.动态障碍物和移动机器人的路径如图10、图11所示，机器人与动态障碍物的实时距离如图12所示.

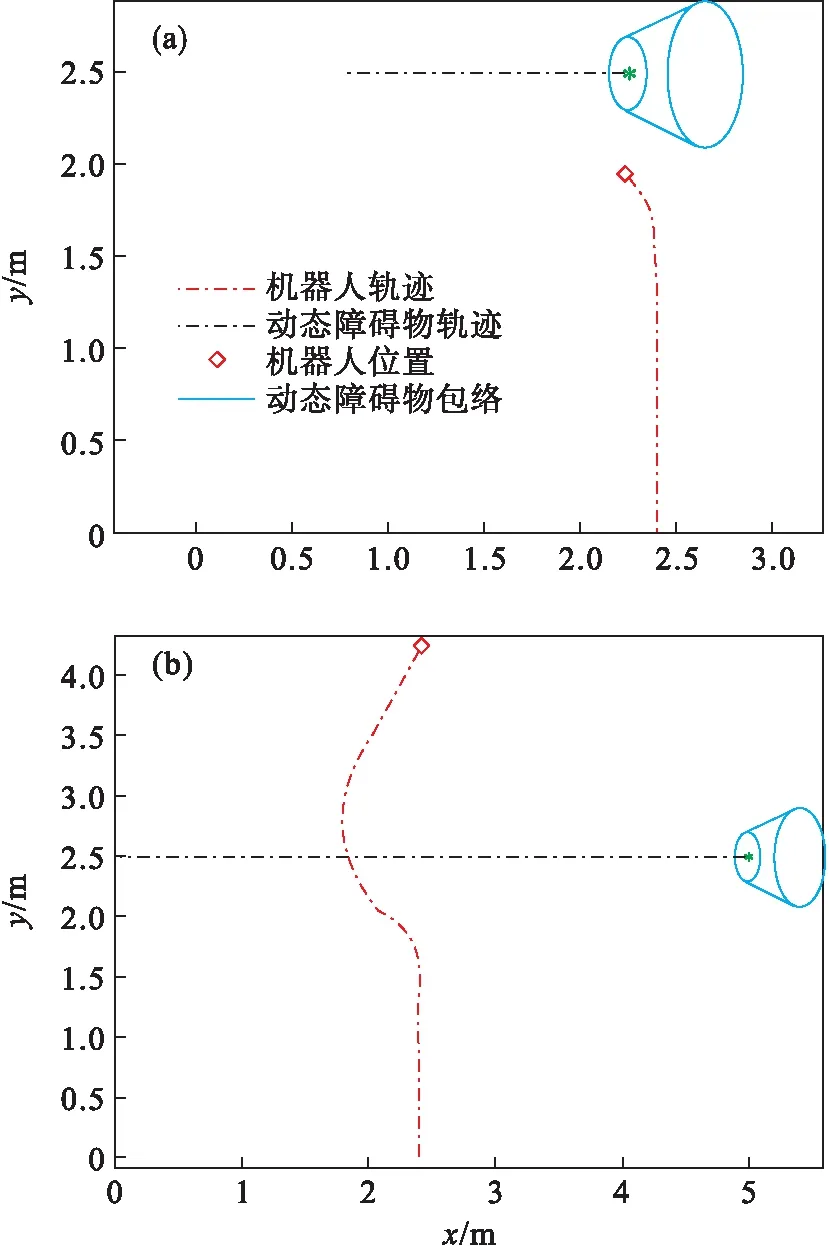
图10 基于多步椭圆包络势场的动态障碍物避障实验Fig.10 Dynamic obstacle avoidance experiment based on multi-step ellipse envelope potential field(a)—t=9 s(本文方法)； (b)—t=20 s.

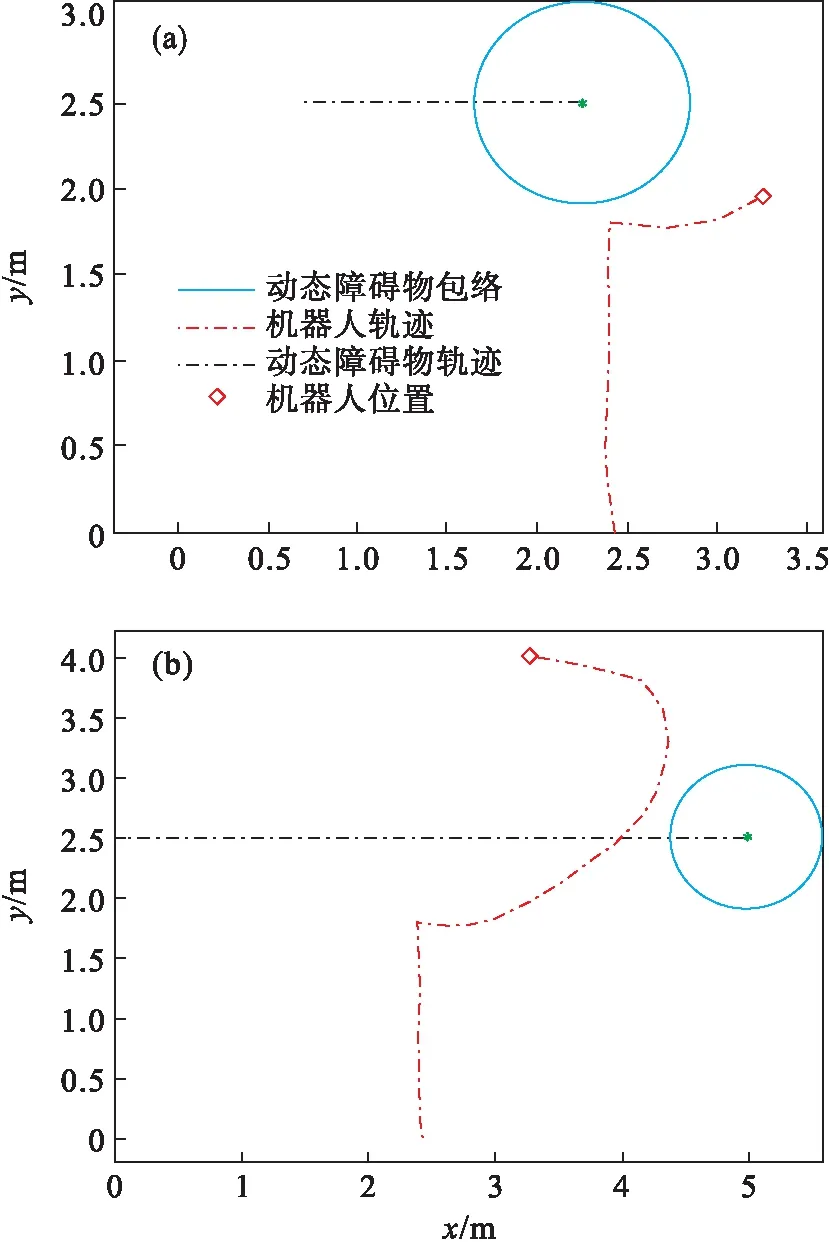
图11 基于人工势场法的动态障碍物避障实验Fig.11 Dynamic obstacle avoidance experiment result based on artificial potential field method(a)—t=9 s(人工势场法)； (b)—t=20 s.

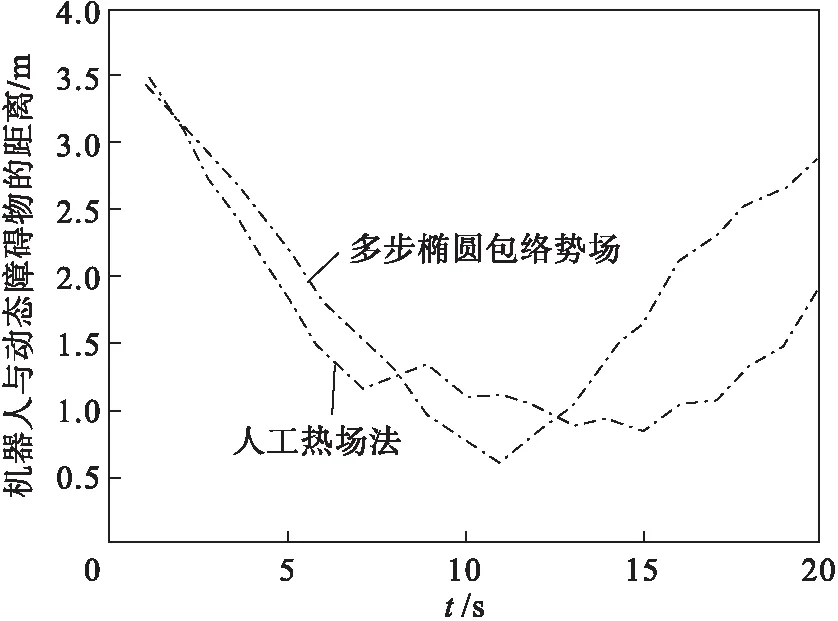
图12 时间对机器人与动态障碍物距离的影响Fig.12 Effect of time on the distance between the robot and dynamic obstacles

选取路径长度、距障碍物最近距离和最大行驶角变化值作为两种方法实验结果的对比指标.两种方法的结果对比如表3所示.多步椭圆包络势场获得的避障轨迹的路径长度和最大行驶角变化值均比人工势场法更优，避障效果更好.这是由于传统的人工势场法虽然可用于实时的避障任务，但只考虑了动态障碍物的当前位置和几何尺寸，忽略了未来运动状态，出现路径绕远问题.基于动态障碍物可达区域预测的多步椭圆包络势场的模型充分考虑动态障碍物的运动特性并对其未来可达区域进行预测，在保证机器人安全运行的前提下，较好地解决了路径绕远问题.

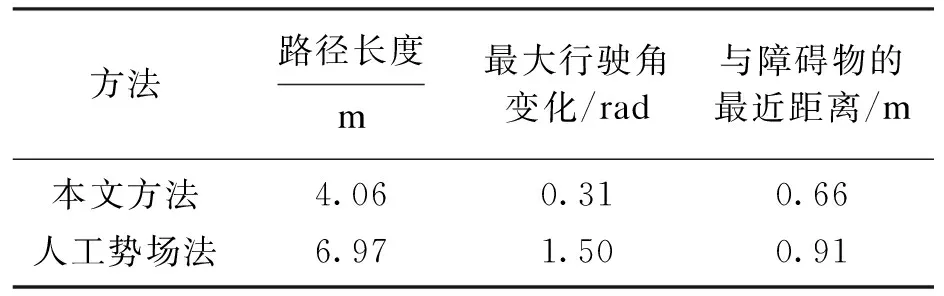
表3 本文方法与人工势场法的结果对比Table 3 Comparison of results of the proposed method and artificial potential field method

6 结 论

本文提出了一种基于障碍物可达区域预测的机器人实时避障算法.建立动态障碍物可达区域预测模型对动态障碍物质心的可达区域进行预测，提出移动机器人实时避障算法，引导机器人向目标点运动的同时规避各类静态障碍物和动态障碍物.实验结果表明，相比于传统的人工势场法和改进型动态窗口法，本文的避障算法在运动距离、距障碍物的最近距离和最大行驶角变化等方面具有显著优势.