小学数学教学中高阶思维能力的培养路径

文/吴仁玉

引 言

在教学中培养学生的高阶思维能力时，教师应注重讲究策略，注重给予学生针对性的引导与启发，增强学生的学习体验和学习成就感，无形之中促进其高阶思维能力的提升。

一、提升课堂例题难度

例题讲解是小学数学教学工作中不可缺少的环节[1]。在教学中，教师应注重将高阶思维能力的培养融入例题讲解中，进一步加深学生对所学知识的认识与理解。一方面，在把握小学数学教学内容的基础上，教师要认真筛选课堂例题，确保选择的例题具有一定的综合性，能够给学生的思维带来良好的启发。另一方面，教师在讲解例题时应注重设计相关的问题与学生进行互动，更好地调动学生思考的积极性。例如，在讲解“比”的知识时，教师可以为学生讲解如下例题：如图1，在△ABC 中，AD:DC=2:3，AE=BE，则甲乙两个图形的面积之比为（ ）。

图1

A.1:3 B.1:4 C.2:3 D.2:5

该题考查三角形面积、比的知识，较为综合，深化学生对“比”知识的理解，锻炼学生的高阶思维能力。教师可以引导学生做辅助线，连接BD，可知△BAD和△BDC 的高相等，而AD:DC=2:3，由三角形的面积公式可知，△BAD 和△BDC 的面积之比为2:3。观察可知△BED 和△EAD 的高相等，而AE=BE，因此，△BED 和△EAD 面积之比为1:1。将△BED 和△EAD 面积均看成1 份，则乙图形的面积为4 份，甲乙两个图形的面积之比为1:4，故选择B 项。

二、优选课堂训练习题

在小学数学教学中，教师及时组织学生开展课堂训练，有助于学生更加牢固地掌握所学知识及解题的思路与方法。在课堂训练中，教师应有针对性地培养学生的高阶思维能力，使学生掌握分析、解答数学问题的相关技巧，感受到数学学习的乐趣[2]。具体来说，教师要严格把控训练习题的难度，确保筛选的训练习题既能够及时巩固学生所学知识，又能使学生的思维得到拓展，并能有效提高学生思维的灵活性。例如，在讲解“扇形”相关知识时，为更好地提升学生的高阶思维能力，教师在课堂训练时可以向学生展示如下习题：如图2 所示，两个圆的半径均为3 厘米，圆心分别为O1、O2，图中两个阴影部分的面积刚好相等，则O1O2的长度为（π 取3.14）（ ）。

图2

A.3.14 B.4.71 C.5.36 D.6.28

该题考查长方形、圆形、扇形知识，乍一看无法下手，实际上只要认真分析、灵活转化，不难解答。解答该题能够很好地培养学生的高阶思维，使其具体思维的灵活性得到提高。因两个阴影部分的面积相等，所以将其均加上S1，则两者的面积也相等。而S1加上上部阴影刚好为圆的说明S1加下部阴影也刚好为圆的，则容易求得长方形的面积为圆的。因为圆的半径为3 厘米，则O1O2×3=×32×3.14，解得O1O2=4.71，选择B 项。

三、重视课堂教学激励

在小学数学教学中培养学生的高阶思维能力时，教师应把握学生的心理特点，重视发挥课堂教学的激励作用，增强学生的学习体验[3]。在教学中，教师应认真观察学生的学习表现，看其是否认真思考问题，尤其当学生正确回答提出的问题时要及时给予表扬，肯定其认真思考的行为，并鼓励其他学生向其学习。另外，为更好地提升学生学习的成就感，教师可结合学生回答问题的难易程度，通过发放小礼品的方式给予学生激励。例如，当学生正确解答出下面的习题时，教师可给学生发放写字笔作为奖励：“黄岩岛是我国南沙群岛中的一个小岛，有着丰富的渔产资源。某一天渔船A 到该区域捕鱼，一段时间后发现一外国船只，该渔船随即向渔政部门报告，并立即返航。渔政船接到报告后及时从港口出发驶向黄岩岛。渔政船和渔船和港口的距离s 和渔船离开刚好的时间关系如图3 所示（假设渔船和渔政船的航线相同）。问渔政船驶向黄岩岛的过程中，渔船从港口行驶多长时间与渔政船相距30 海里？”

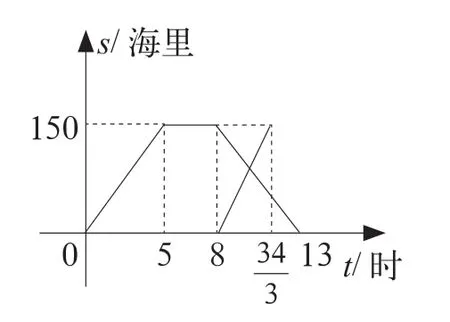
图3

该问题将行程问题和图形结合起来，能很好地考查学生的读图及运用所学分析实际问题的能力。要想解答该题，学生需要从图中挖掘隐含条件，并全面地考虑实际问题。由行程问题可知需要先求出渔船和渔政船的行驶速度，由图3 可知v渔船=150 海里/3 小时=50 海里/小时，v渔政船=150 海里/（-8）小时=45海里/小时。当渔船和渔政船相距30 海里时，可能是相遇前也可能是相遇后。由图3 可知，其一定发生在渔船离开港口后的8 小时以后。则两船未相遇相距30海里时，t=（150-30）海里/（50+45）海里/小时=1.6小时，则总的时间为8+1.6=9.6 小时；两船相遇后相距30 海里时，t=（150+30）海里/（50+45）海里/小时=2.4 小时，则总的时间为8+2.4=10.4 小时。综上，渔船与渔政船相距30 海里时，其从港口行驶的时间为9.6小时、10.4 小时。

四、鼓励学生自主探究

在小学数学教学中培养学生的高阶思维能力时，教师应注重为学生创设相关的探究问题情境，鼓励学生运用所学知识开展自主探究活动，使其参与到数学知识的生成过程中，更好地把握数学知识的精髓。一方面，为更好地激发学生的自主探究热情，教师应保证创设的问题既要具有一定的趣味性，又要能够促进学生高阶思维能力的发展。另一方面，教师要注重跟踪学生的自主探究过程，必要情况下给予学生有针对性的指导，确保其朝着正确的方向进行探究，得出正确的探究结论[4]。例如，在讲解“数学广角”内容后，教师可以提出如下问题要求学生探究。

（1）按照图4（a）的规律，将36 写成几个数的和；

（2）已知1、4、9、16···为“正方形数”，1、3、6、10···为“三角形数”，按照图4（b）的规律将36 写成两个数的和；

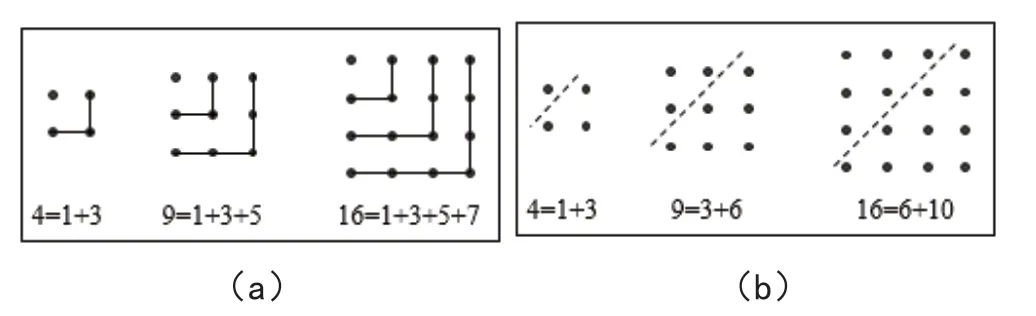
图4

（3）正方形数和三角形数之间有着怎样的关系？

该问题要求学生结合图形进行探究，趣味性较强，能更好地锻炼学生的抽象、概括能力，对提升其高阶思维能力具有重要的促进作用。对于问题（1），可观察图4（a）中的图形以及对应的等式。观察可知，等式右边为奇数之和，所以可推理出36=1+3+5+7+9+11；对于问题（2），根据已知条件，等式左边分别为22、32、42，而等式右边的最小数为上一个等式右边中的最大数，且最大数和最小数的差依次为3-1=2，6-3=3，10-6=4，所以可推出25=52=10+15，36=62=15+21。对于问题（3），通过观察与推理可知任意正方形数可写出两个相邻三角形数之和。

五、注重作业布置深度

在小学数学教学中，教师应将培养学生的高阶思维能力融入各环节，并长久坚持。一方面，教师在布置作业时应注重围绕教学内容拓展作业习题深度，使学生通过做作业积累解决相关问题的经验。另一方面，为更好地调动学生做作业的主动性，教师在布置作业习题时应注重联系生活设计学生熟悉的问题情境，使其体会到应用数学知识解决实际问题的乐趣。例如，“百分数”是小学数学的重要知识点，在人们的生产生活中有着广泛的应用。教师在布置作业时可要求学生结合所学解答如下问题。

某商场为增加销量，按照如下方案搞促销活动：（1）一次购物不超过200 元则不予优惠；（2）一次购物超过200 元，但不超过500 元，按标价低于9 折优惠；（3）一次购物超过500 元，其中500 元按照第2 条规定给予优惠，超过500 元部分给予8 折优惠。小刚的爸爸两次去购物，分别付款178 元与432 元。若他将这两次购买的商品一次性购买，则应付多少元？

该问题并不是简单地进行加减运算，而是需要学生认真审题，充分理解题意，能很好地检验与考查学生的理解能力及灵活运用所学知识的能力。显然解答该题需要根据小刚的爸爸两次付款数求出两次购买商品的原价，而后依据原价及给出的优惠方案进行解答。第1 次付款若超过200 元，则应付200×90%=180元＞178 元，表明第1 次付款并未优惠；若第2 次购买刚好为500 元，则应付500×90%=450 元，可知第2 次付款按照9 折进行优惠，则所购物商品的原价为432÷90%=480 元。两次购买商品的总价为178 元+480元=658 元。显然其符合方案（3），则一次购买需要付款500×90%+（658-500）×80%=450+126.4=576.4 元。

六、启发做好学习总结

无论是日常的教学活动，还是培养学生的高阶思维能力，教师应充分认识到总结的重要性，启发学生定期开展学习总结活动，使其能够认识与及时弥补思维方面的不足。一方面，教师可结合具体教学进度专门留出一节课左右的时间要求学生认真回顾所学，积极开展旧题重做活动，总结相关题型及解题思路。另一方面，针对在学习及训练中出错率较高的习题，教师可以要求学生认真分析出错原因，总结分析问题的切入点，指引其在以后遇到类似问题时能够把握问题本质。

例如，在完成“圆的面积”知识教学后，练习题出错率较高，教师可以要求学生做好解题思路的总结。

如图5 所示，一座长20m、宽10m 的长方形建筑物周围都是草地，使用长30m 的绳子将一只山羊拴在建筑物的一角（图中黑点），则这只羊能够吃到草地的面积是多少（π 取3.14）？

图5

该题需要学生结合自身生活经验，分析绳长与建筑物之间的关系，确定山羊能够到达的活动范围，然后运用所学的几何知识进行解答。根据经验，山羊会围绕图中的黑点旋转，但是旋转的过程中会受到长方形建筑物的阻碍。要想准确地解答该题，学生需要根据生活经验画出辅助线，结合图形进行计算。由图5 可清晰地看到山羊能够到达的区域是半径为30m的个圆，半径为10m 的个圆以及半径为20m 的个圆，则山羊能够吃到草地的面积为×202×π=2119.5+78.5+314=2512m2。

结 语

在小学数学教学中培养学生的高阶思维没有定法，教师需要结合自身的教学实践进行总结、探索，尤其多与其他教师沟通交流，相互学习高效的培养路径，并结合自身实际及学生的学习表现做好细节上的调整，将培养工作有机融入教学活动中，使学生牢固掌握数学知识，有效锻炼与提升高阶思维能力。