一类受媒体报道影响的传染病模型分析

张晓磊，刘茂省

(中北大学 理学院，山西 太原 030051)

对于新出现的传染病，由于缺乏相关数据，如何设计和实施及时、有效的公共卫生干预措施来抑制传染病发展显得很重要，同时市民若遵守政府发布的个人防护和公共卫生干预措施，将会大大降低传染病的发生，这说明在传染病传染期间，政府会通过多种社交媒体工具发布各种关于传染病的消息来对公众进行非药物干预教育，可以降低感染的可能性.

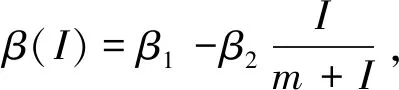
与其他文献不同，本文中，笔者研究了在现实生活中，媒体一报道有关传染病的信息，几乎每个人都会采取措施保护自己不受感染，将这种保护措施实施的执行率，用方程形象地描述出来，最终发现媒体报道会降低传染病的进一步扩散.提出了一个数学模型来研究受媒体影响的传染病的传播，研究了模型稳态的稳定性和分支，通过数值模拟来验证理论证明并进行讨论和总结.

1 模型的建立

基于文献[5]有关Twitter社交软件发布媒体信息来研究和预测流感疾病的EIT模型.将人群划分为4类：易感人群、暴露人群、住院人群和感染人群，分别用S(t)，E(t)，H(t)和I(t)表示其在t时刻其占总人数的比例，M(t)表示在t时刻本地区受媒体传播的传染病信息影响的累计密度.由于研究短期内暴发的传染病，所以忽略了自然死亡和出生率，并假设易感人群数量相对恒定的，故将S视为一个参数.于是，考虑了下面模型：

(1)

假设在传染病传染期间，个体在阅读有关传染病的信息后产生行为变化，进而导致传染病传播率β通过e-aM而降低，其中a反映了传染病信息对传播率的影响程度.假设潜伏个体在1/σd后进入感染阶段，ρI表示感染者的住院率，rI表示感染者不住院的病死率，δ表示住院感染者的病死率，rH表示住院感染者的恢复率.此外以上4类人群分别以μS，μE，μI和μH的速率执行政府发布的关于传染病的信息来降低自身感染的可能性，μ0表示暴发传染病的其他地区的媒体信息传播对本地区的影响，μ表示媒体信息的损耗率.

2 模型的稳定性分析和Hopf分支

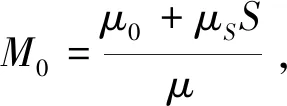
通过计算，可得

则模型(1)的基本再生数

(2)

地方病平衡点E*=(E*,I*,H*,M*)，令模型(1)的所有式子的右端为0，即模型(1)在地方病平衡点E*处满足以下条件：

(3)

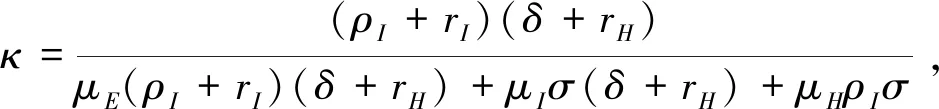
定理1当R0<1时，模型(1)在E0是全局渐近稳定的.

证当R0<1时，模型(1)在E0的雅克比矩阵可以表示为

通过计算得(-σ-λ)(-(ρI+rI)-λ)-σβSe-aM0=0，其中σβSe-aM0=σR0(ρI+rI)，将其代入上面的矩阵得

(σ+λ)λ2+λ(ρI+rI+σ)+σ(ρI+rI)(1-R0)=0，

(4)

则雅克比矩阵的特征根全为负，故E0是局部渐近稳定的.

接下来确定E0的全局渐近稳定性，定义Lyapunov函数：V(t)=E(t)+I(t)，明显V(t)≥0，当且仅当E(t)=I(t)=0时等号成立.

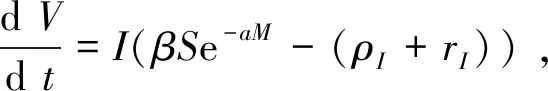
定理2当R0>1时，若p>0且q<0，其中p=μE(σ+μ)-σμI,q=(X1+σ)(X4+μ(X1+σ+μ))(μEX1+σμI)+μX4(μE(σ+μ)+σμI)-(σX3+μE(X4-rHσ-δσ))(X1+σ+μ)2,X1=ρI+rI+δ+rH，X2=ρI+rI，X3=ρIμH+μIrH+μIδ，X4=rHσ+δσ+ρIrH+rIrH+rIδ+ρIδ，则

1) 当Δ>0时，若hh2(h1>0,h2>0)，模型(1)在E*是局部渐近稳定的；

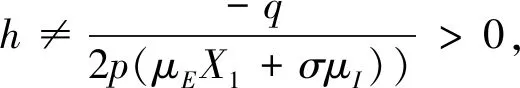
3) 当Δ<0时，对任意实数h，模型(1)在E*是局部渐近稳定的.

其中：Δ=q2-4p(μEX1+σμI)(μX4(X1+σ)(X4+μ(X1+σ+μ))；

证当R0>1时，模型(1)在E*处的雅克比矩阵可以表示为

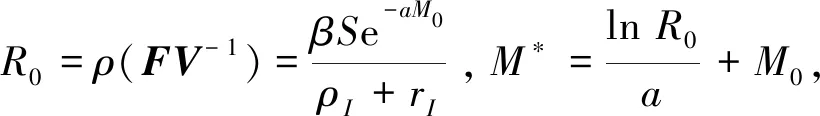
λ4+a1λ3+a2λ2+a3λ+a4=0.

(5)

通过计算此四次多项式可表示为

λ4+(X1+σ+μ)λ3+[aI*μEX2+X4+μ(X1+σ)]λ2+[aI*X2(μEX1+σμI)+μX4]λ+

aI*X2[σX3+μE(X4-rHσ-δσ)]=0,

则a1=X1+σ+μ，a2=aI*μEX2+X4+μ(X1+σ)，a3=aI*X2(μEX1+σμI)+μX4，a4=aI*X2[σX3+μE(X4-rHσ-δσ)]，

其中：X1=ρI+rI+δ+rH；X2=ρI+rI；X3=ρIμH+μIrH+μIδ；

X4=rHσ+δσ+ρIrH+rIrH+rIδ+ρIδ.

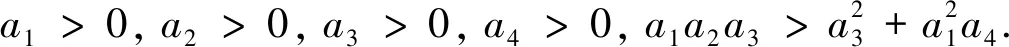
显然ai>0(i=1,2,3,4),经过计算并根据条件可知要保证

a1a2-a3=aI*X2(μE(σ+μ)-σμI)+(X1+σ)(X4+μ(X1+σ+μ))>0,

则必须要有p=μE(σ+μ)-σμI>0.其次要满足

当p=μE(σ+μ)-σμI>0时，可以把上式看作是关于aI*X2的开口向上的一元二次函数H(aI*X2).

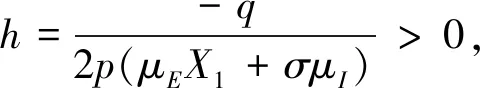
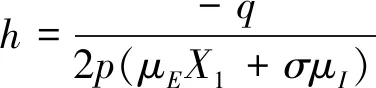
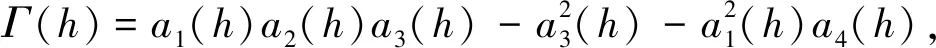
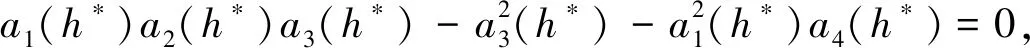
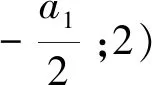
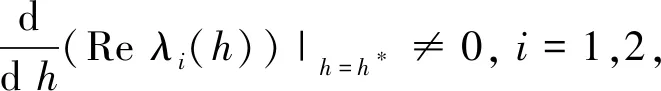
M1(h)c′(h)-M2(h)d′(h)+M3(h)=0，

(6)

M2(h)c′(h)+M1(h)d′(h)+M4(h)=0.

(7)

其中：M1(h)=4c3-12cd2+3a1(c2-d2)+2a2c+a3；

M2(h)=12c2d-4c3+6a1cd+2a2d；

M3(h)=a1′c3-3a1′cd2+a2′(c2-d2)+a3′c+a4′；

M4(h)=3a1′c2d-a1′d3+2a2′cd+a3d′.

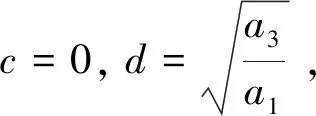
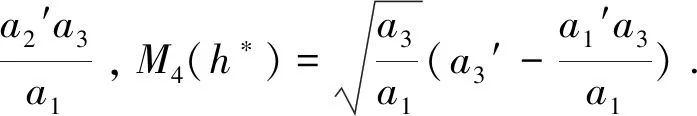
将h=h*代入横截条件可得

3 数值模拟与讨论

易感者、潜伏者、感染者和住院者初值取1 000 000,120,20和1，基于文献[10]设潜伏者到感染者的转移率σ为0.2，设感染者的住院率ρI为0.33.除此之外，假设一旦有人发病，如果不采取措施，不积极住院治疗，其会在短期内有死亡的可能性，故设感染者不住院的病死率rI为0.68，设住院感染者的病死率δ为0.003,住院感染者的恢复率rH为0.13.假设μS=0,μE>0,μ0>0,μI>0,μH>0和μ>0，即只有暴露者、感染者、住院者执行有关传染病信息，因为他们更有可能关注疾病状况.根据实际情况考虑，暴露者由于未被传染仍存在侥幸心理不能足够重视传染病，故在执行有关传染病信息的情况明显比感染者和住院者弱，因此设μE=0.02,μI为0.2,μH为0.301.其次在暴发传染病后，各地都采取隔离措施，使得暴发传染病的其他地区的媒体信息传播对本地区的影响变小，所以设μ0为0.01,其他参数将在数据拟合时进行估计.

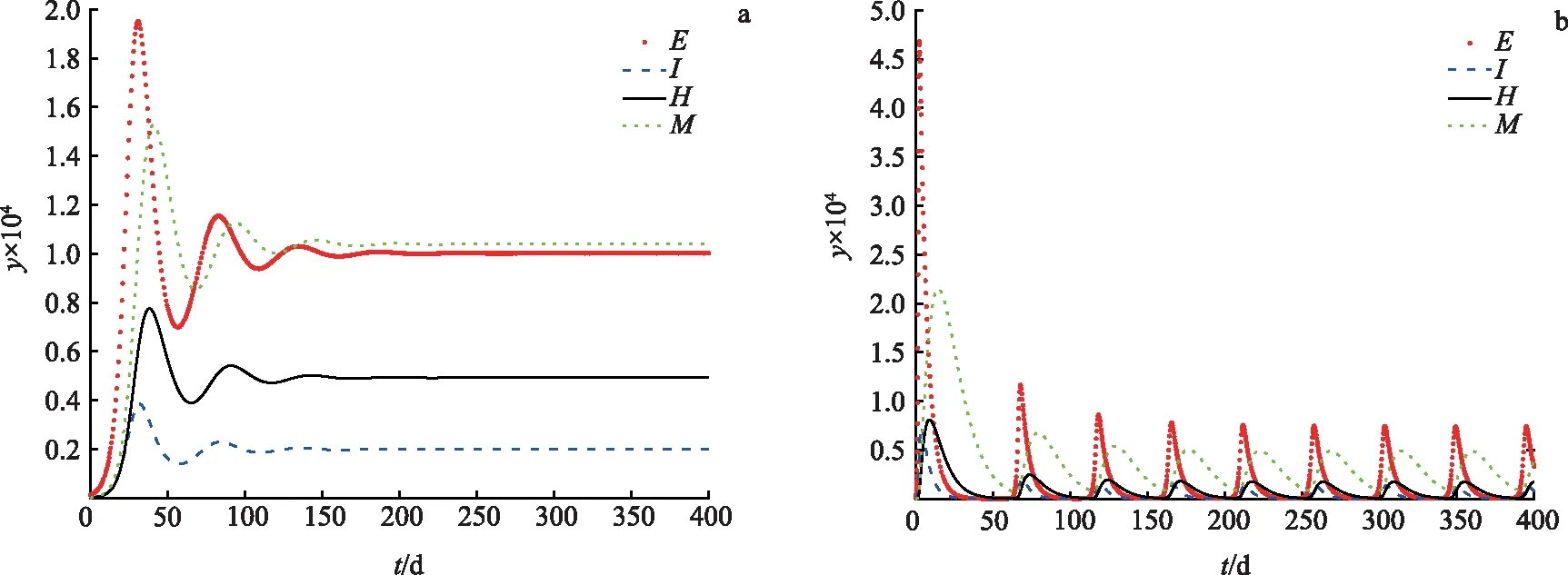
图1 媒体信息报道对传染病动力学的影响Fig.1 The Influence of Media Information Reporting on Infections Disease Dynamic

图1中纵坐标y表示暴露、住院、感染个体数量以及媒体信息的数量.在图1a中β=2.6×10-7，a=1.6×10-5，图1b中β=3.6×10-5，a=8.6×10-3.从图1a中发现，模型的地方病稳态是稳定的.在阻尼振荡后，暴露、感染、住院个体的数量以及媒体信息的数量收敛到稳定状态.图1b中发现，系统收敛到一个持续的周期解，说明如果不强制实行高强度的隔离措施，传染病将一直持续下去，进一步说明在发生重大疫情的情况下，采取封城的措施是抗击疫情的关键，其在很大程度上抑制了疫情的蔓延，同时也发现感染者的高峰出现的时间略早于媒体信息的高峰，此时间延迟可能是由于数据收集和处理所需的时间.

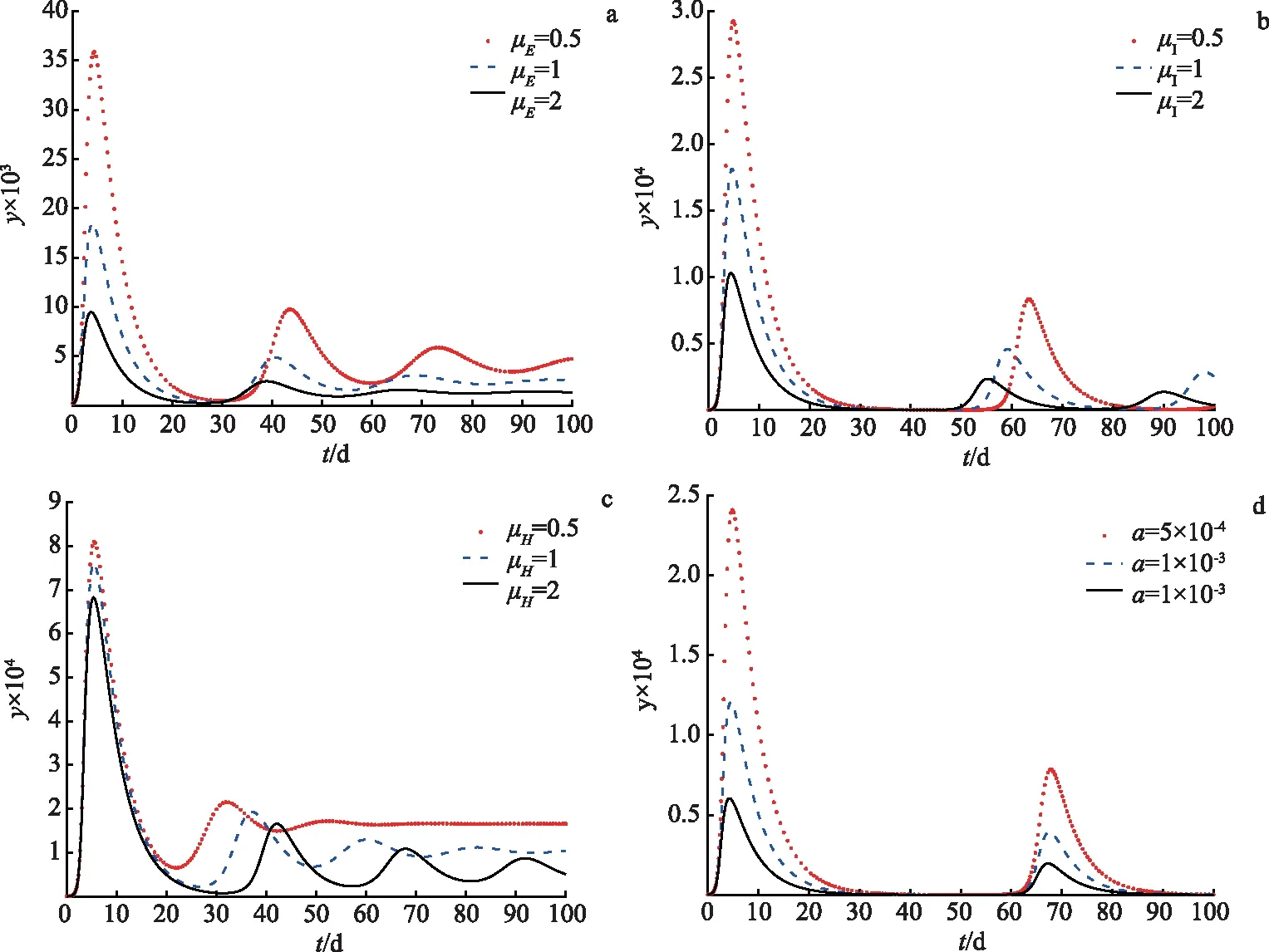
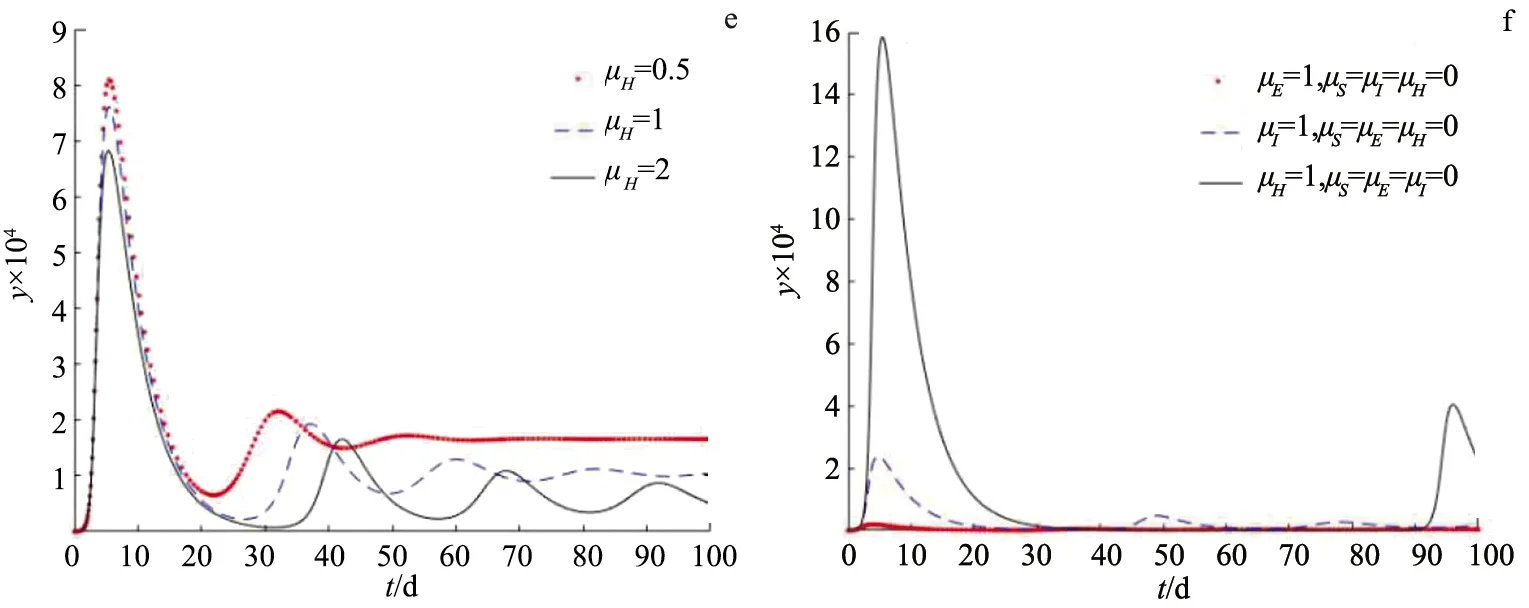
图2 与媒体相关的参数的改变对感染个体动力学的影响Fig.2 Effects of Changing Media-related Parameters on the Dynamic of Infected Individuals

图2中纵标y表示感染个体的个数.在图2a，b，c，d，e，f中,β=3.7×10-6，a=1.5×10-3.评估了媒体信息对疾病动力学的影响，比较了暴露个体、感染个体和住院个体执行率分别为0.5，1和2时感染个体的动态.从图2a，b，c可以看出每天执行的媒体信息越多，感染病例就越低，改变每天执行的媒体信息的数量并不影响疫情达到高峰的时间.图2d比较了媒体信息在不同影响程度下对传染病传播率的影响，发现提高这一比率能显著减少疾病的传播，说明个体受媒体影响的程度将直接影响传染病的进一步发展.从图2e可以看出，假设信息的损耗率分别为0.5，1和2时，信息损耗率越小，个体接收到的信息越多，则感染病例的数量也就减少了.图2f，比较了4种情况下感染者的动态：暴露者、感染者和住院者每天执行媒体发布的相关疾病信息，发现如果暴露者执行这种疾病的信息，那么该传染病在很大程度上被抑制，而只有感染者和住院者执行媒体发布有关传染病的信息，就无法很好地控制该传染病的传播.

总之，在传染病传染期间，媒体信息可能对传染病传播的动态产生重大影响，因此通过媒体对公众进行非药物干预的教育可以降低感染的可能性，媒体信息可以对当前疾病状况作出实时评估，为采取各种干预措施遏制传染病传播提供更多的时间.