一种多尺度估计和自适应响应融合目标跟踪算法

孙德刚，白荣雪，王超，高天学，胡正平,2

(1.山东华宇工学院信息工程学院，山东德州 253000； 2.燕山大学信息科学与工程学院，河北秦皇岛 066004)

0 前言

为了缓解跟踪样本边缘产生的边界效应，尽可能提升跟踪精度和鲁棒性，本文作者结合时域正则化和空域正则化来解决相关滤波跟踪时的边界效应问题，提取目标的基础手工特征和深度特征，通过降维方法加速算法运算，并利用尺度池方法估计目标尺度，提升跟踪效果。

深度网络框架由于其训练过程导致速度大多比较慢，与相关滤波结合的孪生网络速度优势比较大。WANG等提出端到端的轻量级孪生网络体系结构(Discriminative Correlation Filter with Network,DCFNet)算法，在网络的一层加入相关滤波器，将网络输出作为响应图并推导反向传播的过程依然在频域进行，因此在深度算法中速度较快。HONG等将离线CNN图像库为背景，利用网络的隐藏层输出描述特征，并结合反向传播和在线SVM构造目标显著图，被称为CNN-SVM算法。此外，端到端学习和注意力机制等也常用于视频处理中。为了尽可能提升跟踪精度和鲁棒性，本文作者将相关滤波与深度特征相结合，并在现有算法基础上从特征、模型等多方面进行改进。

1 多尺度估计和自适应响应融合目标跟踪算法综述

本文作者提出基于卷积特征的多尺度估计和自适应响应融合目标跟踪算法，来解决相关滤波跟踪框架中深度特征跟踪优势受限和计算存储冗余等问题。首先提取目标区域的手工和深度卷积特征，通过学习连续域卷积算子实现多分辨率特征的融合；其次，通过调整高斯标签参数，充分利用手工特征的准确性，深入挖掘深度特征的鲁棒性；然后，通过分解卷积操作对深度特征进行有监督降维来减少模型参数，为了减少样本冗余并保留正确样本，进行基于高斯混合模型的动态样本融合，并使用模糊稀疏的模型更新机制提高模型更新的有效性；最后，根据预测质量评估标准，对深度特征和手工浅层特征的跟踪响应图进行自适应融合。此外，还分别使用PCA和正交三角分解方法对平移滤波器和尺度滤波器特征进行降维，并使用三角插值法进一步提高跟踪精度。

1.1 基于连续卷积算子的目标跟踪

在将多层深度卷积特征用于相关滤波跟踪时，由于不同卷积层具有不同的图像分辨率，超出了相关滤波只能处理单分辨率图像的限制。为了集成多分辨率深度特征图，文献[6]提出连续卷积算子方法，在图像训练之前应用空域隐式插值将特征图插值到连续空域。一方面，该方法在连续域中执行卷积来实现多分辨率特征图的自然集成，这样就可以独立灵活地选择每个视觉特征的分辨率，而无需显式重采样；另一方面，以连续函数的形式求出目标的跟踪响应，从而实现子网格的精确定位，进一步提高相关滤波的跟踪精度。

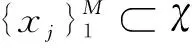
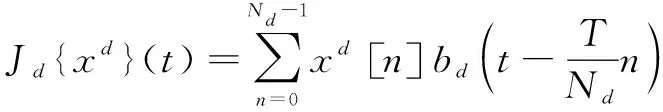
(1)

训练一个连续周期多通道卷积滤波器=(,…,)来预测目标的检测分数：

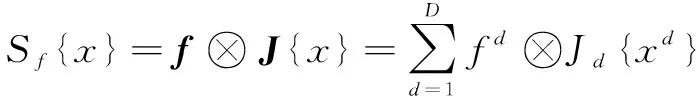
(2)

1.2 连续卷积算子跟踪优化算法

连续卷积算子目标跟踪算法，利用训练样本的隐式内插模型来学习连续空间域中的卷积算子，通过学习的卷积滤波器，可以产生目标的连续域置信图，使相关滤波器跟踪实现对多分辨率特征映射的融合。但复杂的计算使算法无法达到实时要求，在一定程度上限制了算法的实际跟踪应用。本文作者结合文献[7]提出的几点改进措施，进一步设计对于连续卷积算子跟踪算法的优化方法。

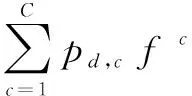
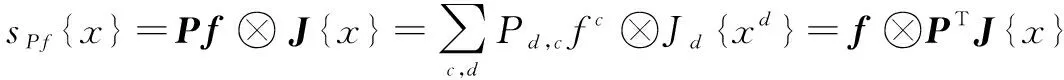
(3)

上式的最后一步可以看作是降维数据的重组，首先降维矩阵与位置处的特征向量{}()相乘求出维降维特征图，然后再与滤波器卷积。是通过公式(2)和公式(3)最小化分解算子的分类误差，再判别联合地学习滤波器和矩阵而得到的。

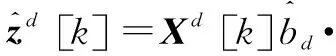
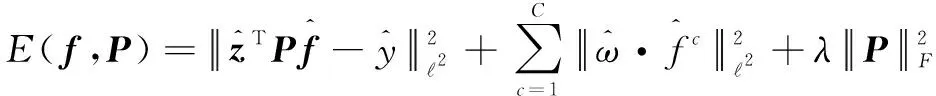
(4)

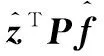
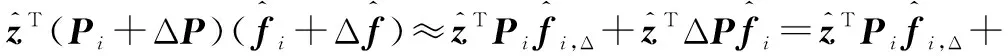
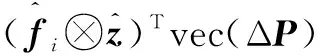
(5)

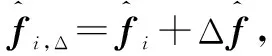
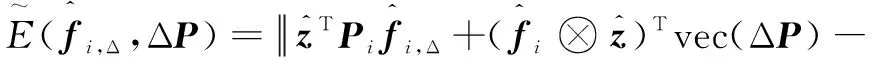
(6)

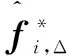
以上分解卷积算子过程中的降维矩阵只需要在第一帧时学习，而后直接用于特征降维来提高运算速度。这样在后续跟踪时，有利于减少投影特征图{}所占用的内存空间，滤波器更新时也可以直接利用{}将特征图由维降至维，以此达到节约内存和减少计算量的目的。

1.3 基于GMM的动态样本融合

在以往的跟踪算法中，每跟踪一帧图像就相应添加一个训练样本，由于跟踪样本的外观变化是时空连续的，所以该样本权重设置为由学习率控制的指数衰减～(1-)-，当样本数达到上限时，最小权重的样本将被新样本替换，这种更新策略需要较大的样本限制才能获得比较具有代表性的样本集。否则，若采用上述逐帧添加新样本的策略，将会使空间有限的样本集被大量相似的样本占用，产生过多冗余信息，不能涵盖样本的多样性。本文作者采用混合高斯模型(Gaussian Mixture Model,GMM)提高样本差异性，将相似的样本融合为一个样本分量，并始终保留第一帧样本分量，最终生成由各具差异性的样本分量构成的紧凑型的样本集来缓解上述问题。文中使用基于GMM的动态样本融合策略，通过赋予第一帧稳定的权重，并动态调整样本分量的权重，使样本集中的样本数量从降至，且保持了每个样本分量的高效性和对样本形变的适应性。

1.4 模糊稀疏模型更新策略

理论上，最合理的模型更新方式是选择在目标外观发生一定程度的变化之后进行更新，但实际上目前还很难找到一个相对简单且计算量小的判别目标外观变化程度的指标。综合以上分析，使用稀疏的模型更新方式，间隔一定帧数更新一次跟踪模型。借鉴已有的实验结果，模型更新间隔处于一个动态范围内时跟踪效果更好。本文作者在稀疏的模型更新方式上使用模糊策略，使算法在一个区间[,]内随机选择更新间隔，则采用模糊稀疏策略的模型更新次数降至：

=[∑()](-+1)

(7)

其中:是跟踪视频序列的总帧数;是使用的更新间隔，取[,]区间内的整数。使用模糊稀疏的模型更新策略，在一定程度上可以缓解因遮挡和运动出视野等导致模型腐化的问题，提高了跟踪算法模型更新的有效性和计算效率。

1.5 自适应响应融合策略

深度特征(如VGGNet)近几年越来越多地应用于目标跟踪领域。但研究表明，计算耗时的深度特征无法从更深卷积层获益，这与深度学习性能随着网络的增大和加深而更优的原则相悖。为了充分发挥深层和浅层特征的跟踪优势，本文作者差异化对待两种特征，更关注深度特征的鲁棒性和浅层特征的精度，并在响应阶段使用自适应融合策略。

参考已有预测质量评估标准，对跟踪精度和鲁棒性进行量化。从响应图的情况来看：一方面响应图的峰值越尖锐，表明其定位能力更精准；另一方面主峰与邻近干扰峰的边际越大表明当前预测置信度明显高于其他候选位置，说明跟踪鲁棒性强。所使用的评价目标预测质量的最小化权重置信边际指标为

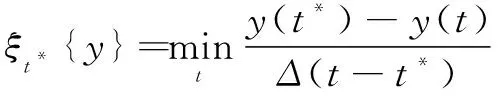
(8)

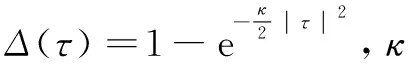
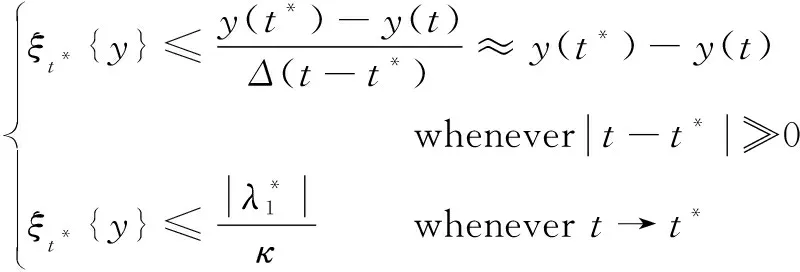
(9)

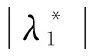
在响应融合阶段，基于在响应融合阶段提出的预测质量评估标准，对深度特征响应()和浅层特征响应()分别以权重和进行加权融合：

()=()+()

(10)

以上求解通过建模来最小化损失函数：

subject to:+=1,≥0，≥0

(11)

其中：是正则项参数。

引入松弛变量={}，公式(5)可以优化为

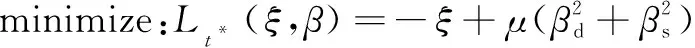
subject to:+=1,≥0,≥0

()-(-)≥(),

∀∈

(12)

通过采样有限组候选状态来求解该问题，每组是含有3个变量的二次规划问题，这种问题可以用常规标准方法来求解，计算量增加不大。通过调整高斯标签函数参数，并根据预测质量评估方法进行自适应响应融合，发挥了深度特征的跟踪鲁棒性和浅层特征的跟踪精度特性，有利于进一步提高目标跟踪效果。

对于尺度估计，采用7个比较粗的尺度池方法，平移滤波器从尺度池内的缩放图像检测出响应最大的目标位置和尺度，检测得到位置和尺度的全局最优结果，检测得到的不一定是位置和尺度各自局部的最优结果。本文作者借鉴尺度金字塔方法，并结合降维思想，将这种高效精细的尺度估计方法用于文中算法。

2 实验结果与分析

2.1 实验环境与参数设置

实验环境为Intel Core i5-4200 CPU，主频1.6 GHz，内存8 GB，64位Win10操作系统，实验平台为MATLAB R2016b。模型更新间隔区间[,]取[5,7]，深度和浅层特征的标签函数标准差分别是=14和=116，预测质量评估的控制参数以8为因子与目标大小成反比，响应融合阶段的正则项参数=015，尺度金字塔的尺度因子=1.02，文中算法OursHC使用FHOG、CN和gray特征，OursDeep使用FHOG和VGG-M网络的Conv1和Conv5。

为了评估算法性能，选取OTB-2013和OTB-2015作为测试数据集，选取的数据集中每个视频序列具有一种或多种挑战因素，测试数据更具有代表性。采用OTB数据集的一次性通过评估OPE模式，选择跟踪的距离精度和重叠率精度作为评价指标。文中设定阈值为20像素，阈值为0.5。将文中使用的深度特征算法OursDeep和手工特征算法OursHC与DeepSRDCF、CNN-SVM、SiamFC3s、CFNet、DCFNet、SRDCF、DSST共9种流行算法进行比较，验证文中算法框架和使用深度特征的有效性，并做定量和定性分析。

2.2 对比实验定量分析

测得9种算法在OTB-2013和OTB-2015数据集的平均距离精度()和平均重叠率精度()见表1，图1和图2分别为9种算法在OTB-2013和OTB-2015数据集中11种视频属性的距离精度和成功率，其中第一幅曲线图是平均跟踪结果。为便于数据对比，将9种算法在OTB-2013和OTB-2015数据集中11种视频属性下的跟踪成功率和距离精度结果列在表2和表3中，其中加框数据表示最优结果，加下划线数据表示次优结果。

表1 OPE模式下9种算法的平均跟踪性能 单位：%

结合表1可知:在OTB-2013数据集上，文中深度特征算法OursDeep的平均和平均分别为90.5%和68.2%，手工特征算法OursHC分别为86.4%和65.0%，在OTB-2015数据集上;文中深度特征算法OursDeep的平均和平均分别为89.0%和67.0%，手工特征算法OursHC分别为83.5%和62.7%。与其他几种深度算法相比，文中使用深度特征的算法超越了性能较好的DeepSRDCF以及使用孪生网络框架的DCFNet、CFNet和SiamFC3s算法，使用手工特征的算法获得了较优的跟踪结果。与同样采取判别相关滤波和深度特征的DeepSRDCF算法相比，在OTB-2013数据集上的精确度和成功率分别提升了5.6%和4.1%，在OTB-2015数据集上分别提升了3.9%和3.5%，表明文中算法具有较好的跟踪性能。

由图1可知:在11种挑战因素中，文中算法OursDeep在其中10种因素的跟踪精度均排在第1名。但在图像序列低分辨率情况下，文中算法跟踪效果略高于DCFNet算法，接近于SiamFC3s和CFNet算法，与采用CNN和SVM构造目标显著图的CNN-SVM算法相比，还存在一定差距。另外，文中手工特征的算法OursHC在尺度变化等7个挑战因素中均排在第2名，说明算法总体跟踪精度较高。

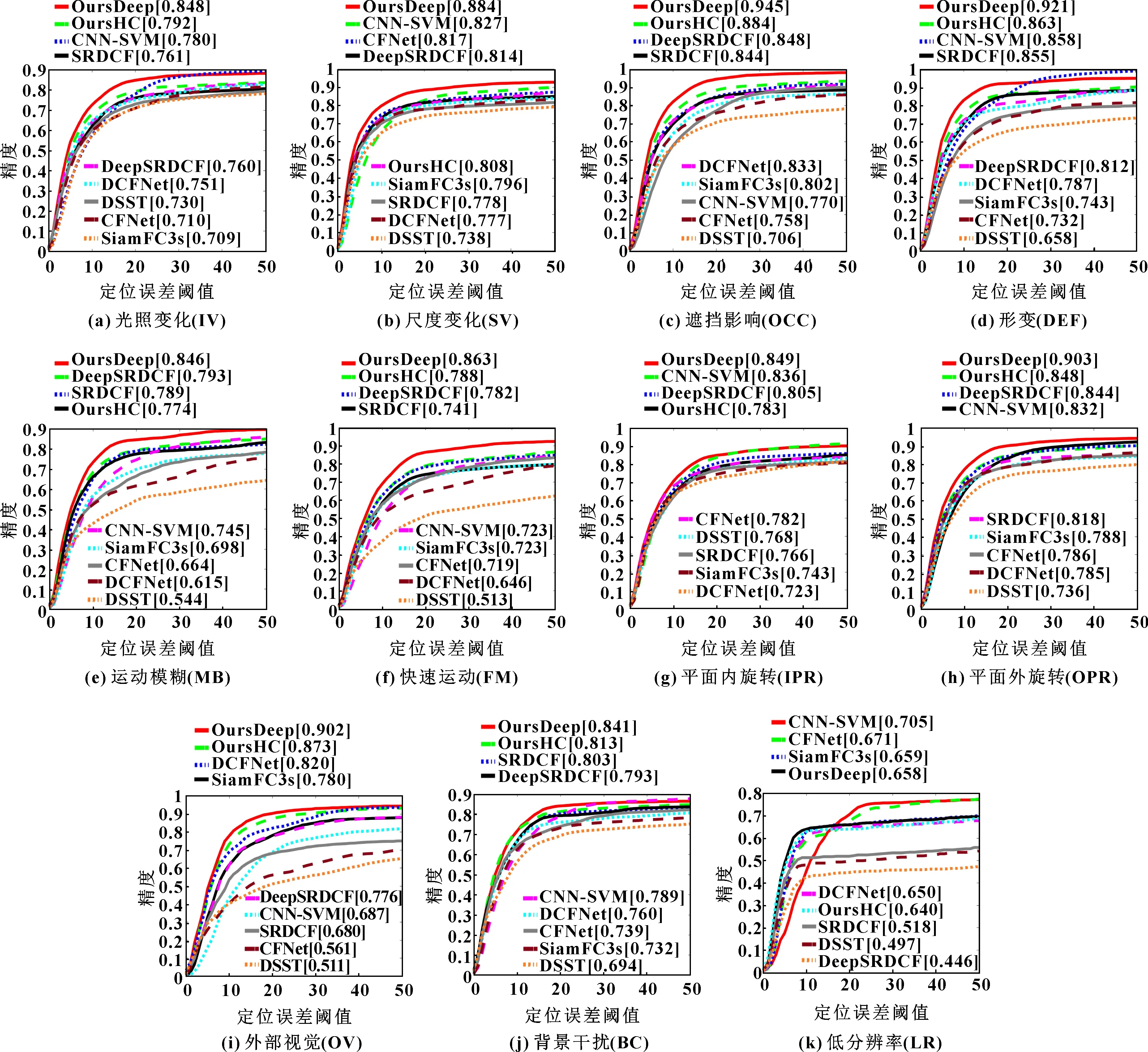
图1 9种算法在OTB-2013数据集11种挑战因素的距离精度图

由表2可更直观看出:在对11种挑战因素的跟踪成功率测试中，文中算法跟踪效果优势比较明显，尤其是对具有障碍物遮挡和运动出视野等挑战因素时，文中算法相比DeepSRDCF算法跟踪成功率提升8%以上，对低分辨率图像跟踪效果有待改善。

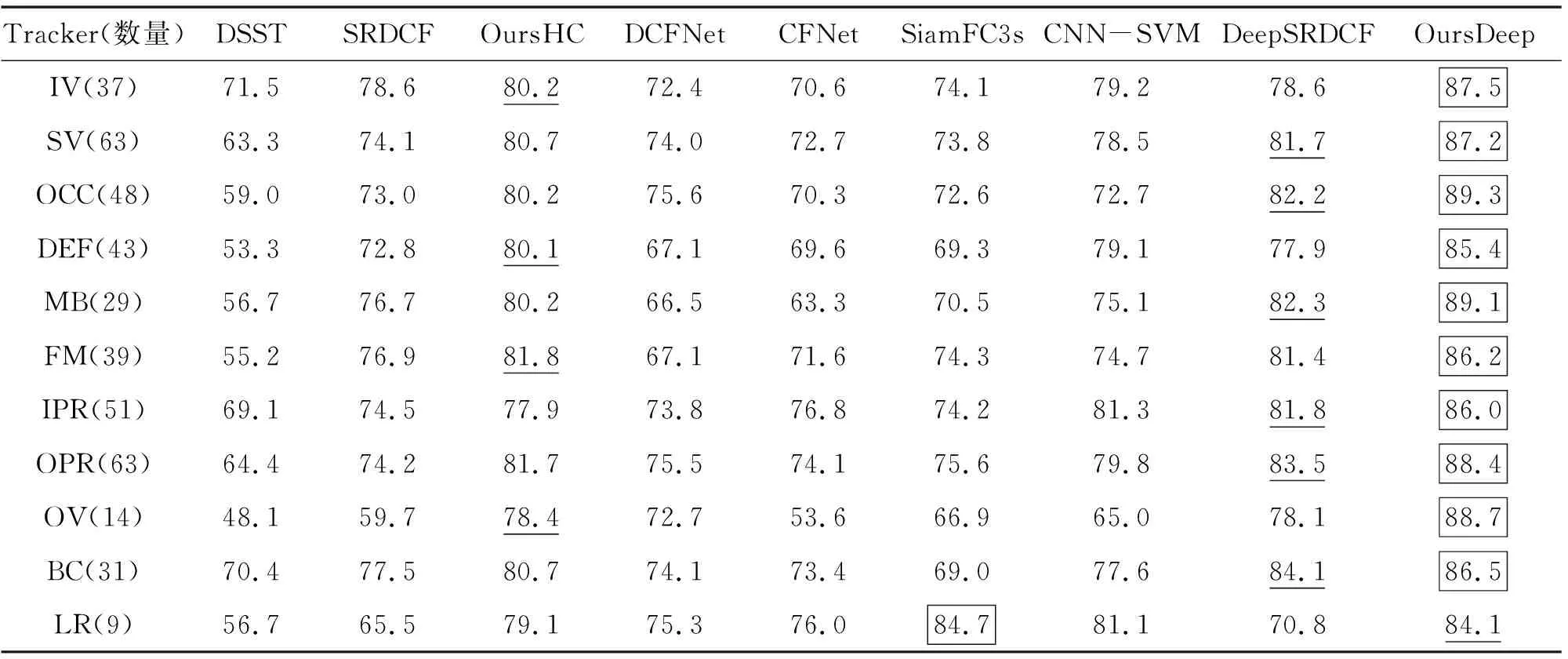
表2 OTB-2013数据集中9种算法在11种挑战因素的跟踪成功率 单位：%

由表3可知:在数据量更多的OTB-2015数据集中，测试的跟踪趋势与OTB-2013数据集大体一致，但随着测试数据的增多，在11种视频属性的挑战因素中，文中算法相对于DeepSRDCF算法的跟踪优势依然明显，说明文中算法的整体跟踪性能较好，适应性较强。

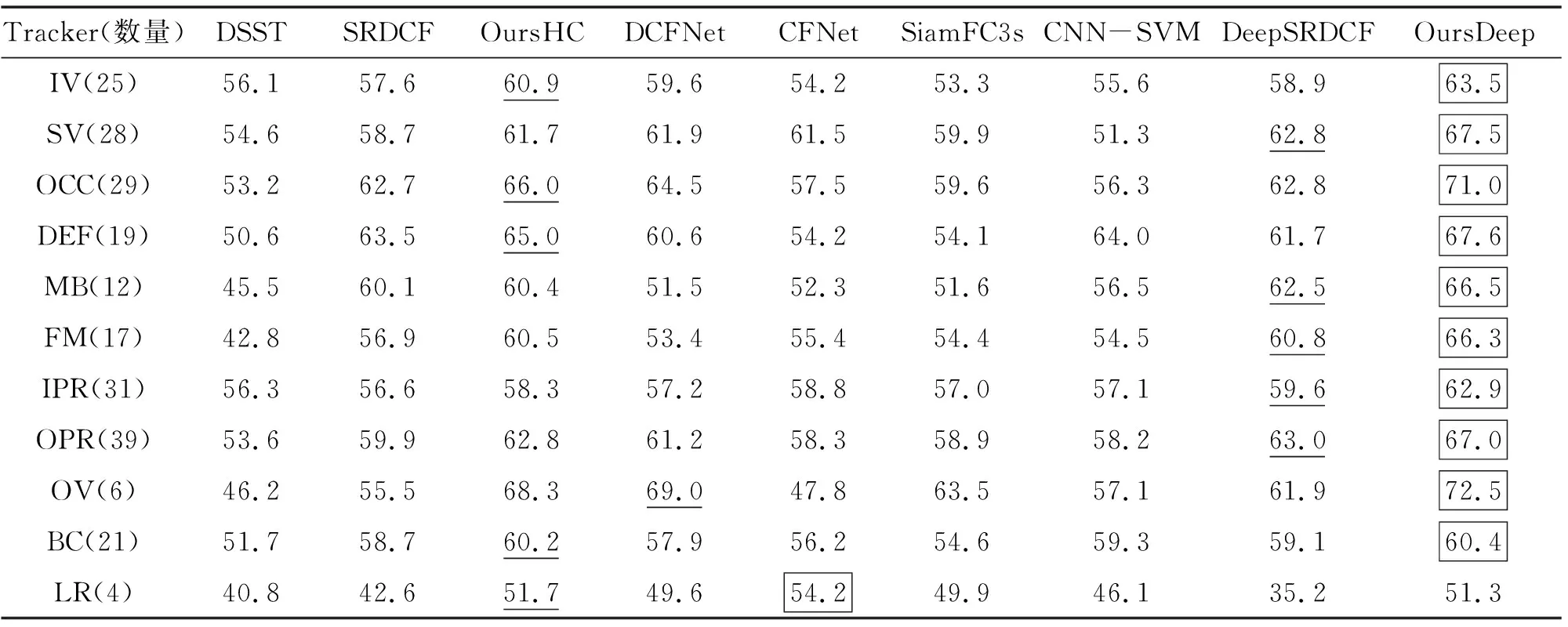
表3 OTB-2015数据集中9种算法在11种挑战因素的跟踪距离精度 单位：%

结合图2可知：文中算法在11种挑战因素的10种因素中成功率依然排名第一，且手工特征OursHC的跟踪成功率在其中9种因素中排名前三，跟踪效果稳超很多深度学习框架算法。

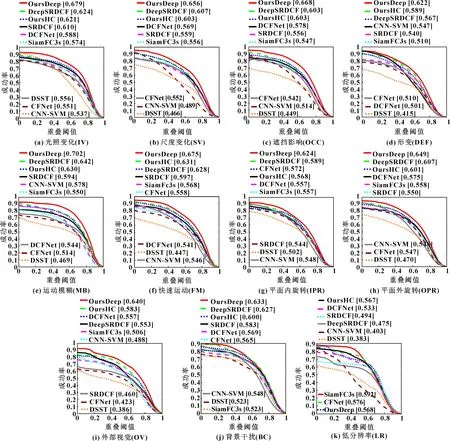
图2 9种算法在OTB-2015数据集11种挑战因素的成功率

综合各图和表显示的结果可知:与参与对比的其他算法相比，文中设计的算法总体跟踪距离精度和成功率均排在第1名，在11种视频属性的测试中，在10种上具有较大优势。从文中算法自身对比来看：采用深度特征的OursDeep比单纯使用手工特征的OursHC跟踪距离精度和成功率均有较大提高，其跟踪效果在数据较多的OTB-2015数据集测试中分别提升5.5%和4.3%，说明深度特征的使用作用明显。

2.3 对比实验定性分析

选取6组具有多种挑战因素的视频序列对文中算法进行分析，各视频包含的视频属性、帧数等信息见表4，选取的视频序列包含多种挑战因素，数据的多样性更具有说服力。

表4 6组视频序列的属性及相关信息

文中采用稀疏更新模型并且对深度特征和手工特征的响应图进行自适应融合，在出视野、形变、低分辨率等情况下的稳定性较好，对目标的综合跟踪能力较强。

3 结论

提出基于卷积特征和响应融合的目标跟踪算法，从特征、学习更新方式和响应融合等几个方面进行改进。首先，引入手工特征和多层深度卷积特征，通过学习连续域卷积算子实现了多分辨率特征的融合，并通过调整高斯标签函数参数，充分发挥了两种特征各自跟踪优势；然后，通过分解卷积操作，对深度特征进行有监督降维，并利用基于高斯混合模型的动态样本融合，保留正确样本的同时提高了样本差异性，使用的模糊稀疏更新机制缓解了遮挡情况下因模型退化导致的跟踪失败问题；最后，根据预测质量评估指标，对深度特征和手工特征的跟踪响应图进行自适应融合，发挥特征各自在不同跟踪场景中的跟踪优势。