基于后验预测分布的机器人焊接质量监控研究

吴姝，何雨飞，屈挺，胡楷雄

(1.武汉理工大学物流工程学院，湖北武汉 430063； 2.暨南大学智能科学与工程学院，广东珠海 519070)

0 前言

在传统焊接工作中，焊工要长时间面对高强度电磁辐射、热辐射、电弧光、一氧化碳等有毒气体、射线和烟尘等极度恶劣的环境，对其身体健康有很大危害。为避免这一情况，同时也为在保证焊接质量的前提下，提高焊接生产效率，增强企业的综合竞争力，很多企业逐渐开始使用焊接机器人取代焊接工人，以实现焊接技术的无人化、智能化、柔性化。焊接机器人的工作原理是在工业机器人的机械臂末端安装焊枪，并将焊枪送达空间预定位置，按程序设定的轨迹及速度移动，使之具有高品质工业焊接的能力。

在实际焊接作业过程中，焊缝质量检测是确保机器人焊接质量的重要手段，主要手段包括外观检验、无损探伤(射线检验、超声检验、磁粉检验、渗透检验)等。由于焊缝检测点较多，缺陷数判别效率较低，故目前焊缝缺陷点检测样本量都较小，各学者和制造企业都在着重研究小样本条件下监控焊接质量等相关问题。

传统方法在小样本环境下的应用收效甚微，并且多基于计量型控制图，鲜有涉及计数型控制图。本文作者基于共轭贝叶斯理论，提出一种动态计数型控制图监测焊缝缺陷数方法。从历史数据中获取合适的先验信息；根据当前监测信息，建立贝叶斯后验预测分布模型，实现动态监测；通过实例比较文中方法与现有常用方法。结果表明，所提方法在各个阶段都有更好的监测效果和异常检出力，可为机器人焊接质量提供一种有效的监测方法。

1 控制图设计

控制图称为缺陷数控制图，是一种计数型控制图﹐其控制对象是一定单位(如长度、面积和体积等)上的缺陷数。本文作者采用此控制图进行方案设计。

已知参数的控制图一般模型为

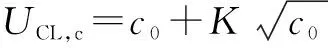
其中：为受控情况下的产品缺陷数。

假设,1,…,,(=1,2,…)为Phase II阶段的独立样本数据，即：

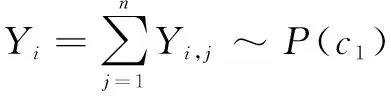
其中：为失控状态下的产品缺陷数。

1.1 基于矩估计的c控制图设计

频率统计学派在无法确定所需的分布参数时，一般选用矩估计对概率分布参数进行统计推断。假设在Phase I阶段有组容量为的样本,1,…,,(=1,2,…,)且均满足独立同分布，因此有:

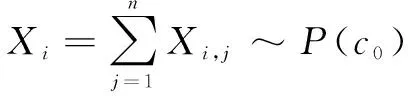
其中:～()。从而给出基于矩估计的控制图模型为

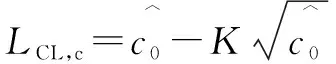
但只有在样本容量足够大的时候才可以将矩估计结果视作较为精确的结果。相关研究已经证明只有当样本容量为50以上时，上述结论才可认为是基本成立的。

1.2 基于后验预测分布的c控制图设计

共轭先验是先验信息确定方法中最重要的一类，共轭贝叶斯估计也是一种常用的贝叶斯估计方法，因此视先验分布和后验分布来自同一形式，且形成一个先验链，即先验分布和样本分布通过计算得到的后验分布与先验分布具有相同的形式，此时的先验分布和样本分布则被视为具有共轭性，而此时的先验分布就被称为共轭先验分布。采用共轭先验分布的贝叶斯估计就被称为共轭贝叶斯估计。

(1)=(,…,)是从总体中获得的当前样本数据，均服从泊松分布()。因此给出似然函数：

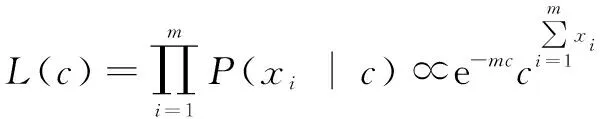
(2)确定分布参数的先验分布。在未抽取样本时，可以通过()对作出一个初步估计，然后确定超参数。当样本分布为泊松分布()时，根据共轭贝叶斯理论，泊松分布的先验分布取伽马分布(,)，则的后验分布仍为伽马分布，其密度函数为

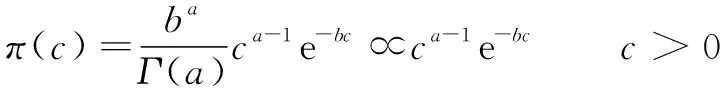
其均值和标准差分别为

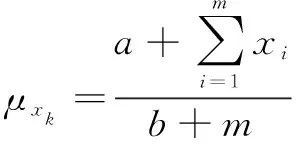
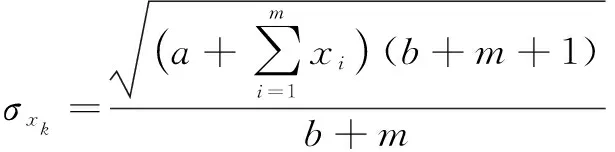
从而给出基于共轭贝叶斯理论计算出的后验预测分布的控制图模型为

=-

=+

1.3 性能分析

运行长度(Run Length,RL)是指控制图从开始描点监测直到第一个出界点出现为止，一共描点的次数。运行长度分为受控状态的运行长度和失控状态的运行长度。根据数学和期望的统计特点，可以用平均运行长度(Average Run Length，ARL)和运行长度标准差(Standard Deviation Run Length,SDRL)表示控制图的优劣。受控状态时的平均运行链长记为，失控状态时的平均运行链长记为。越大表示控制图误报率越低，越小表示控制图的漏报率越低，即异常检出力越强。SDRL表示运行链长变化的幅度,越小说明监测过程稳健性越好。本文作者根据几何分布性质对贝叶斯控制图的、、SDRL进行计算与分析，并通过蒙特卡洛仿真进行验证。

假设贝叶斯控制图在Phase I阶段得到的后验预测分布参数为、，则在受控状态下参数不变，发生出界事件的概率为

=1-(∣,)+(-1∣,)

在失控状态下后验预测分布参数变为、，发生出界事件的概率为

=1-(∣,)+(CL，-1∣,)

则描点次数变量服从几何分布，有：

()=(1-)-1

()=1-(1-)

根据几何分布的性质可知：

=1/

=1/

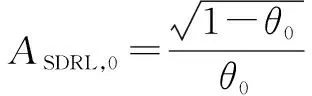
设定=3,={10,20,30,…,100},={10,20,50,100,200},=(1+),失控状态下均值发生的漂移={01,02,05,20}，根据伽马分布数字特征，先验分布取=05、=。用几何分布法，计算、与、，并与似然估计方法进行对比，结果如表1—表5所示。

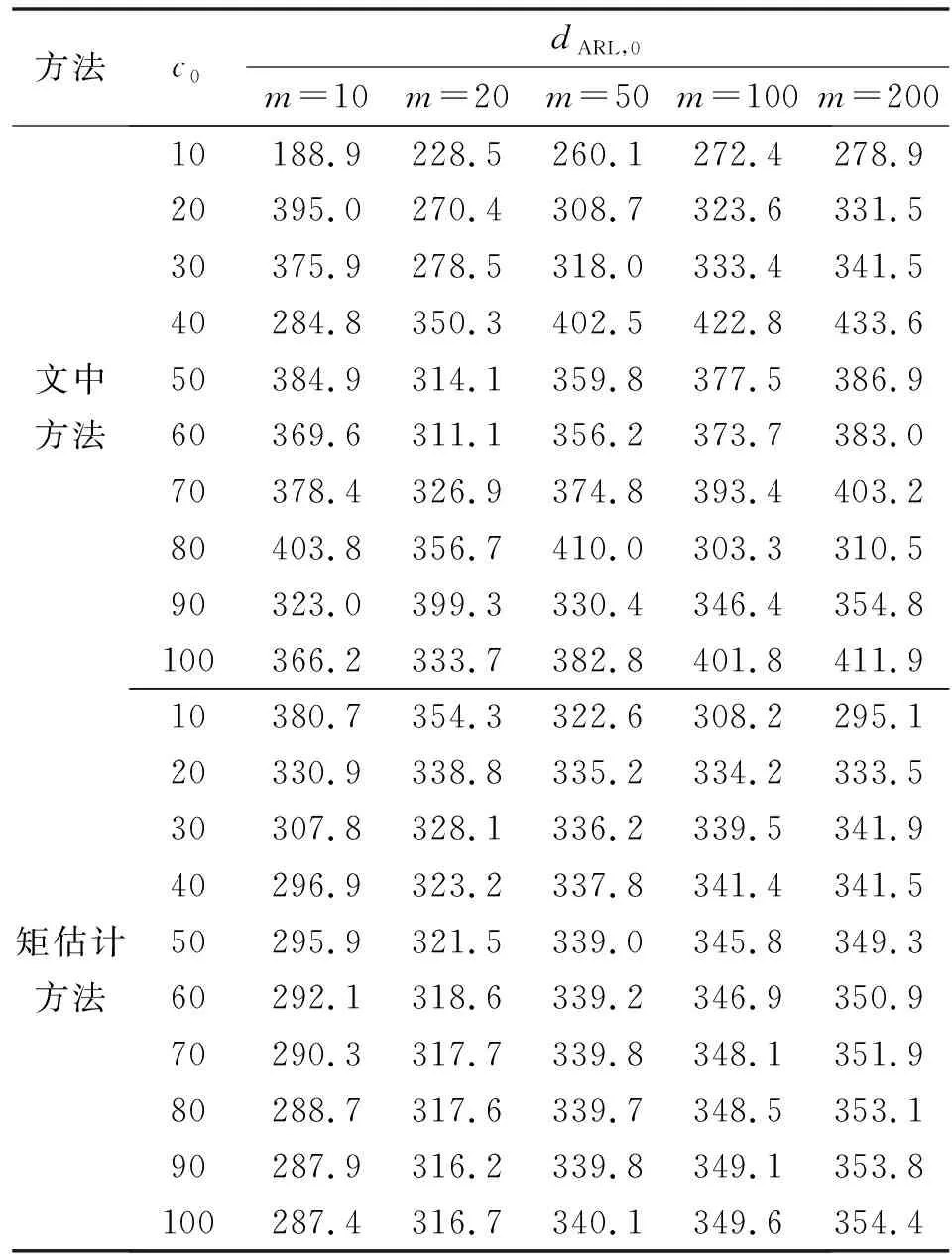
表1 受控状态下，文中方法dARL,0与矩估计方法对比结果

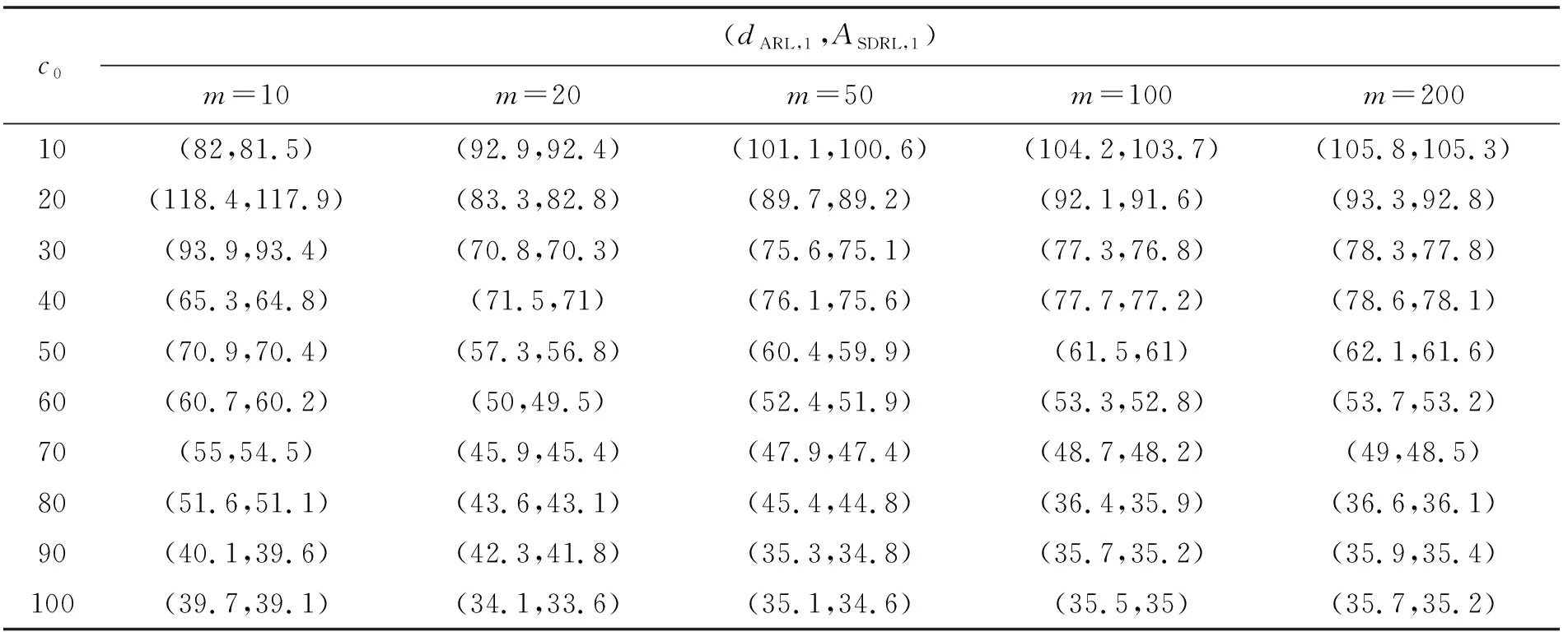
表2 失控状态(dARL,1,ASDRL,1),δ=0.1

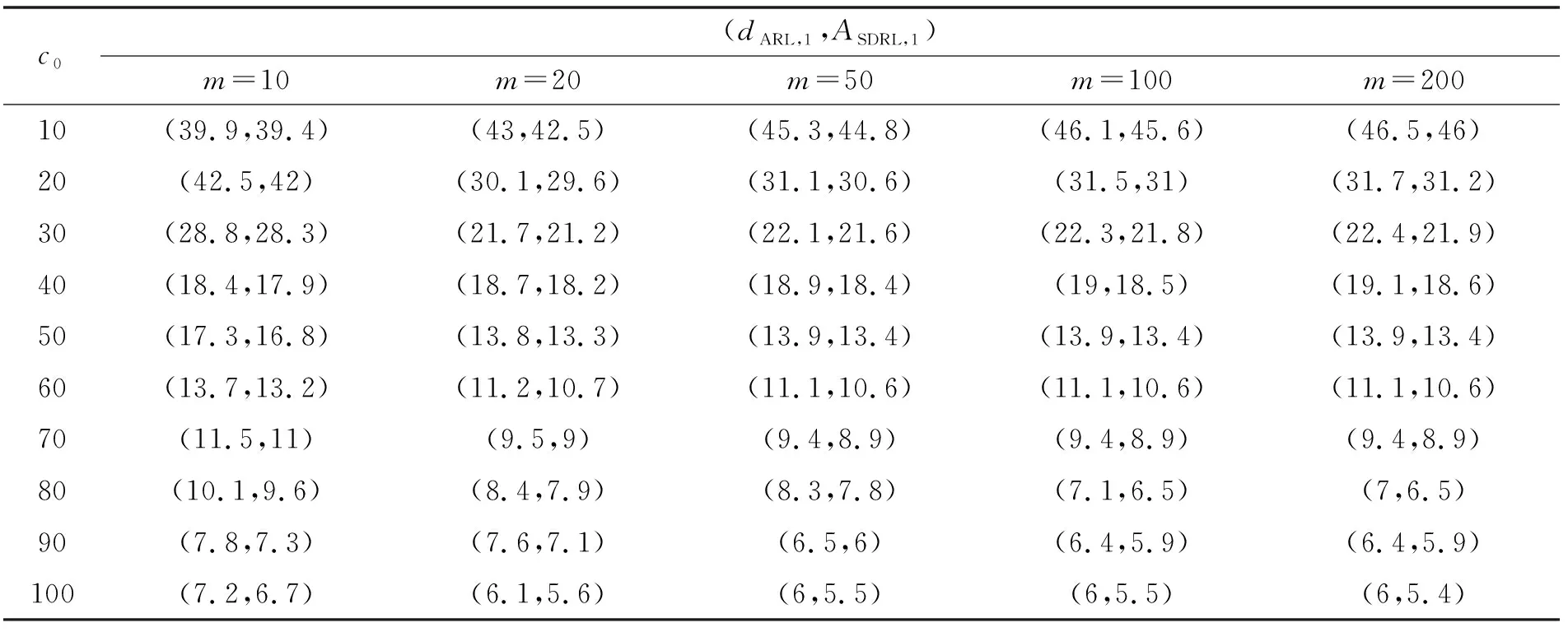
表3 失控状态(dARL,1,ASDRL,1),δ=0.2

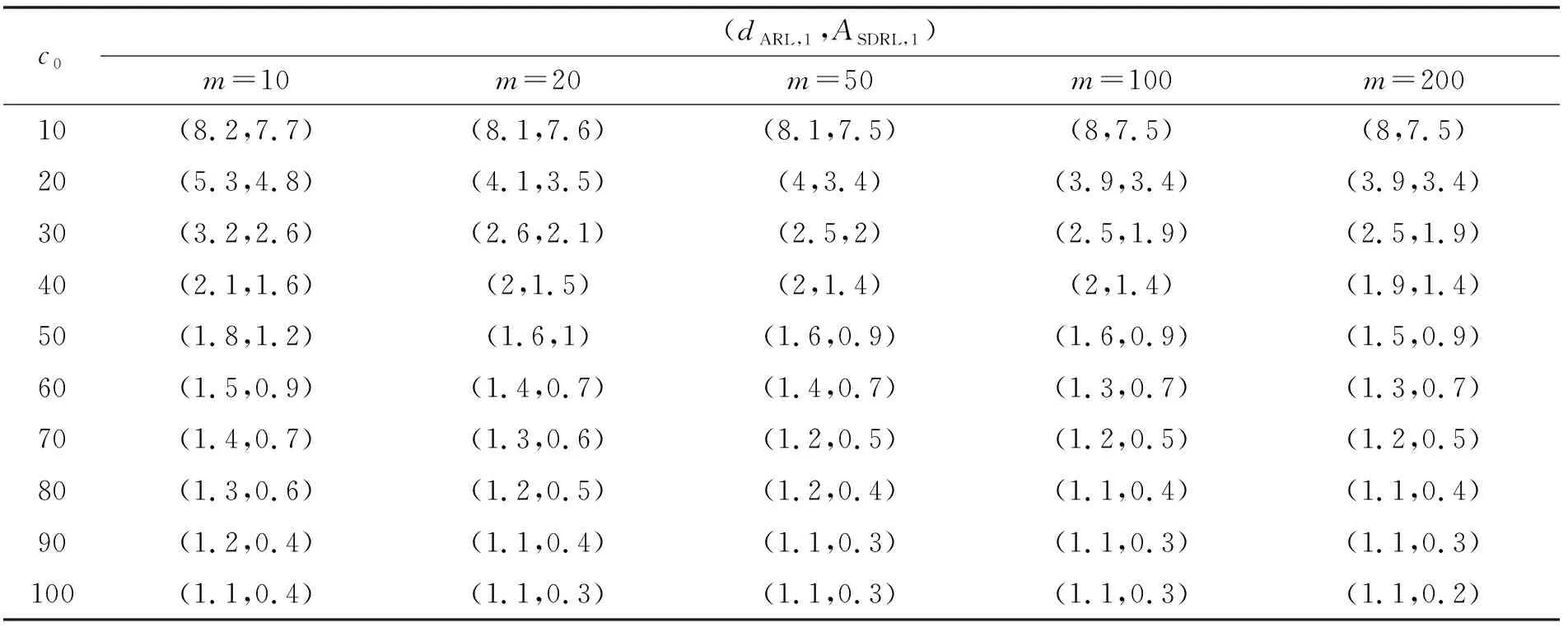
表4 失控状态(dARL,1,ASDRL,1),δ=0.5

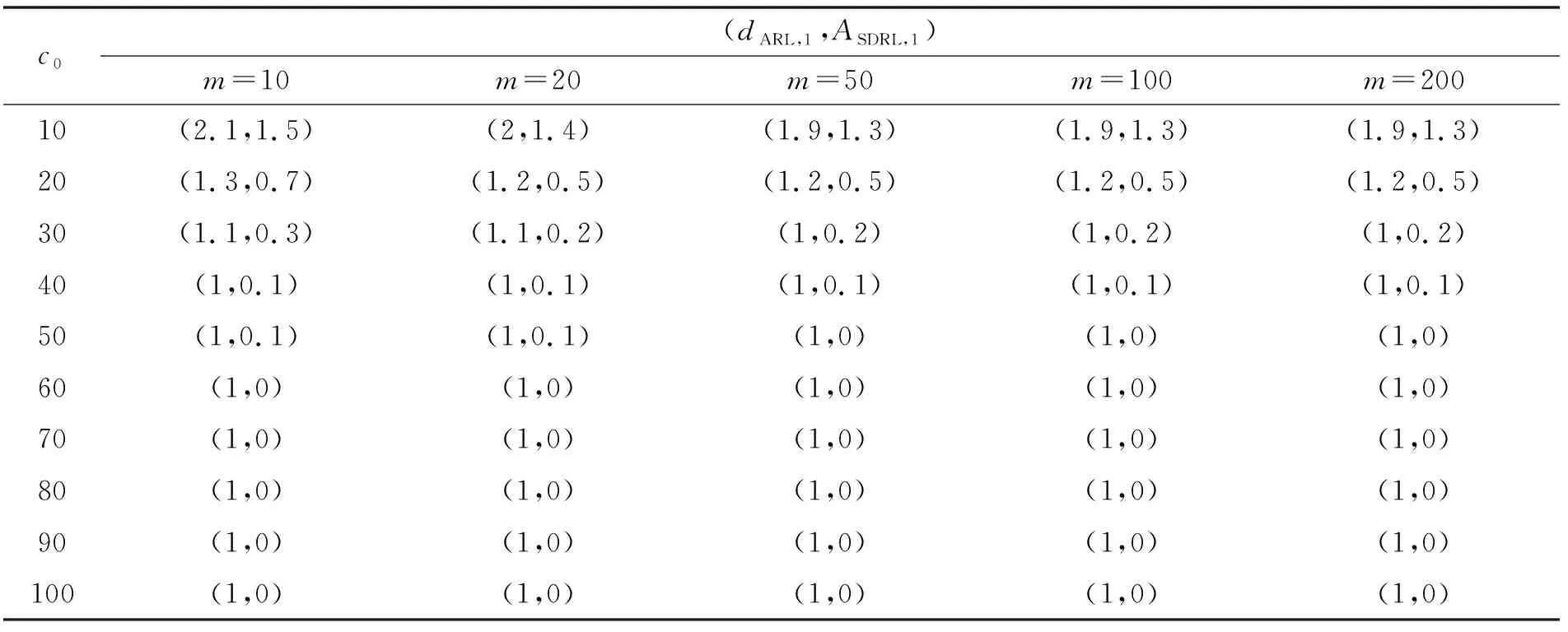
表5 失控状态(dARL,1,ASDRL,1)，δ=1.0

用于验证的蒙特卡洛仿真方法过程如下：

步骤1，根据泊松分布()生成Phase I的个样本数据，应用文中方法计算控制限；

步骤2，根据泊松分布()生成受控状态Phase II的数据，计算从开始描点到控制图报警之间的运行链长；

步骤3，从步骤1至步骤2记为完成一次仿真,一共进行10 000次仿真；

步骤4，计算和。

和同理，根据泊松分布()生成失控状态Phase II的数据并进行计算。

仿真结果与几何分布法计算结果基本一致，故上表中平均运行链长计算结果具有可靠性。由表1—表5可以看出：

(1)由于图的离散性，当发生变化时，不可能对所有考虑值都有一个共同的值。已知当=3时，计量型均值控制图的为370.4，那么对于图，值有时较小，有时大于370.4，计数型控制图不够灵活的缺点显而易见。

(2)对于，当较小，即Phase I阶段样本量较少时，尤其当为10～20时，文中方法的明显大于传统方法，控制图具有更低的第一类错误率，在受控状态下的监控稳定性更强。

(3)对于，当较小，即Phase I阶段样本量较少时，尤其当为10～20时，文中方法的明显小于传统方法，控制图具有更低的第二类错误率，在失控状态下的异常检出力更强；在缺陷数均值漂移较小的情况下，依然能保持较高水平的异常检出力，改善了传统控制图在这方面的不足。

(4)对于，在失控状态下，无论样本均值是发生较小偏移还是较大偏移，贝叶斯控制图在监测过程中都保持了较好的稳健性。

2 实例验证

实验平台主要由机器人、焊接设备、焊缝扫描设备三大部分构成。其中，机器人部分包括机器人本体、控制柜和手持控制器;焊接设备部分主要由焊枪、送丝机、电源等组成。将焊枪加装在某公司生产的KR16R1610型通用工业机器人的机械臂末端上便可将它改装为工业上普遍采用的焊接机器人，如图1所示。

图1 KUKA机器人焊接平台

本文作者以此实验平台为基础，将等厚钢板作为焊接对象，在同一工作现场、同一程序设定条件下进行机器人焊接作业，并对焊缝缺陷进行扫描，建立控制图相关数学模型，为焊接机器人质量监控提供一种实验分析手段和实证支持。

抽取19块焊接成品(见图2)作为质量监测样本。使用激光传感器对已焊接钢板进行扫描，得到焊缝各检测点的三维坐标。由于传感器工作时为逐行扫描，故可计算每一检测行的平均凸度，判别它是否为异常检测行，以此得出每块钢板上焊缝的缺陷数，作为控制图的质量监测特征。

图2 焊接钢板成品

计算焊缝凸度实质上就是计算焊缝截面轮廓上的点到轮廓端点、间线段的距离。具体计算过程如下：

(1)通过扫描数据确定端点的坐标值,拟合出以、为端点的二次函数=++，其中、、为二次函数系数；和之间的线段为无缺陷的焊缝端面轮廓,所在直线记为++=0；

(2)通过各检测点的位置坐标(,)，计算点到焊缝端面轮廓所在直线的距离，并计算出该检测行所有检测点的平均距离，作为该检测行的凸度;

(3)通过3方法设定最大凸度，凸度超过最大凸度的检测行即为缺陷行，计入该焊缝缺陷数。

由此，检测得到19块钢板样本的缺陷数，如表6所示。

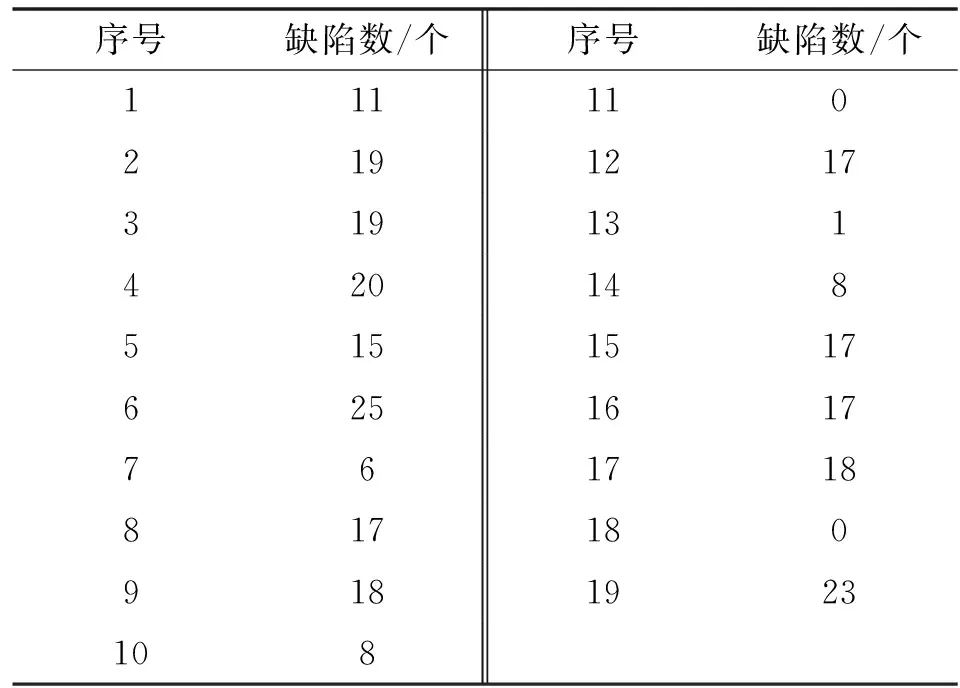
表6 钢板焊缝缺陷数

用矩估计方法计算控制限，对应控制图如图3所示。

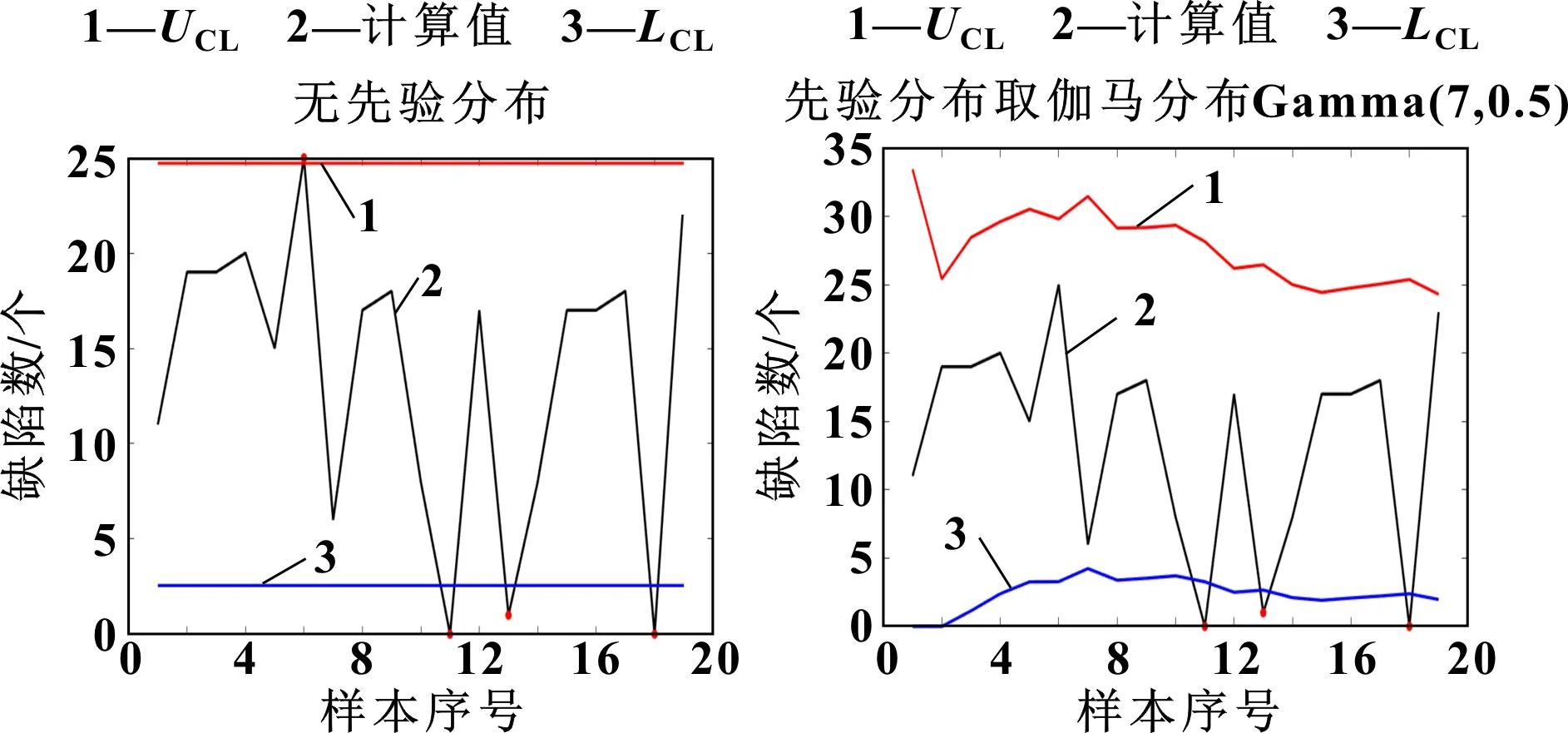
图3 基于矩估计的c控制图 图4 基于后验预测分布的c控制图

对标准化后的历史数据样本进行方差分析和Bartlett检验的齐性处理，挑选出与当前批次样本具有相似工序的先验信息，得到先验分布Gamma(7,0.5)，并用后验预测分布方法计算控制限。对应控制图如图4所示。

由图3、图4可知，传统的矩估计方法在只有19个样本量的情况下很难绘制出效果较好的控制图，而文中方法能避免信息缺失带来的控制限误差，尤其适用于小样本下的焊缝质量监控，具有更好的监测效果和异常检出力。

3 小结

针对机器人焊接质量监控问题，本文作者基于后验预测分布，改进传统控制图，提出一种贝叶斯动态控制图。与传统方法相比，该方法在一定程度上解决了在样本量较小情况下当前样本数据不足所导致的质量控制问题。在数据收集初期，当前批次的样本容量小时，经贝叶斯估计得到的后验信息相较于当前批次样本信息估计，能在很大程度上降低控制限失真程度。