考虑建筑物遮蔽的电力应急通信基站选址双层优化方法

王志强，董忠涛，王骁龙，刘文霞，毛宇洋，黄易君成

考虑建筑物遮蔽的电力应急通信基站选址双层优化方法

王志强，董忠涛，王骁龙，刘文霞，毛宇洋，黄易君成

(新能源电力系统国家重点实验室(华北电力大学)，北京 102206)

电力应急通信基站仅依靠人的主观经验部署存在不足。因此，考虑建筑物对基站信号的遮蔽影响，基于单兵前往灾区勘测的回传信息，对研究问题进行图形化描述。在此基础上，提出了电力应急通信基站选址的双层优化模型。上层以基站间信号传输损耗最小为目标，在划定的基站可选位置范围内，针对非线性模型，利用粒子群算法优化基站的预选位置。下层以基站间信号传输路径与建筑物的间隔距离最大为目标，利用支持向量机优化基站的最终位置，并传递回上层以计算信号传输损耗，通过迭代优化获得基站的最优部署位置。通过在算例中与单层模型比较，验证了所提方法的可行性与有效性，可为发生重大自然灾害后电力应急通信网的搭建提供技术参考。

电力应急通信基站；跨区域部署；建筑物遮蔽；信号传输损耗；双层优化；粒子群算法；支持向量机

0 引言

近年来，由地震、洪涝等自然灾害引发的电网大面积停电事故给社会带来巨大损失，灾害后电网的快速抢修是降低停电损失的关键[1]。但在重大自然灾害面前，公共通信网和电力专网也可能因遭到破坏而陷入瘫痪，这将阻碍电网抢修工作中信息的上传下达[2]，此时，可以通过部署应急基站解决灾区与电网调度之间的通信问题，然而两地间高大建筑物对基站信号的遮蔽效应，给基站的部署带来困难。该问题的解决对于保障电网抢修工作的后续开展、最大化降低停电损失具有重要意义。

目前，国内外学者对电力应急通信基站的位置优化问题关注较少，而对于非应急状态下基站的选址问题，学者们已进行了大量研究[3-8]。文献[3]以通信网络规划区域内基站建设数目最少和信号覆盖率最大为目标，利用改进免疫算法求得基站选址方案；文献[4]提出基于量子免疫算法的基站选址优化方法，该方法能以较少的基站数目满足信号覆盖率要求；文献[5]考虑了覆盖率、容量以及基站数目要求，将变步长人工鱼群算法应用到基站选址优化问题。总的来说，非应急状态下基站选址问题的研究，综合考虑信号质量、基站数目以及覆盖率约束，将基站候选位置集合中的基站个体视为0-1变量，通过智能优化算法求解基站候选位置集合的一个子集，得到基站最优布局，并对模型求解算法做出较多改进。但是，应急状态下的基站位置选取，除了考虑基站实现对受灾地区的信号覆盖，还需要建立灾区内基站与灾区外电网调度中心之间的信号传输路径，即实现跨区域通信。

关于应急状态下灾区内部与电网调度中心之间信号传输路径构建以及对灾区现场的信号覆盖，有学者对整体方案进行了研究[9-16]。文献[9]提出在灾区抢修现场搭建无线自组网，现场移动终端通过无线方式接入自组网骨干节点；与电网调度中心通信时，采用卫星通信方式。文献[10]提出部署应急基站实现对灾区现场的信号覆盖，现场数据依靠卫星通信技术传送到电网调度中心。考虑到卫星通信成本较高，也有学者提出通过搭建无线基站，实现灾区与调度间的信息传送，文献[11]除了在灾区现场部署基站外，在灾区外存在公共通信网的区域部署另外一个基站，两基站通过无线中继方式建立信号传输路径，灾区外基站通过接入公共通信网与电网调度中心进行通信。在基站间的通信过程中，发信方信号发射功率与接信方信号接收强度的差值为信号传输损耗，最大通信距离对应允许的最大信号传输损耗；为满足救灾场景下远距离跨区域通信的需求，车载应急基站大多采用定向天线，但天线的信号绕射能力稍差、架设高度有限，若信号传输路径受到建筑物较大程度遮挡，信号损耗数值可能过大，致使区域内外通信需求得不到满足。此外，目前应急基站主要依靠现场人员的工作经验部署，为实现跨区域通信，人员反复调整基站位置可能花费较多时间。为提高应急通信网络搭建速度，给电力抢修提供保障，建立模型来优化选取两个基站的位置，使其能更好地规避高大建筑物的遮蔽，实现灾区内、外的良好通信。

综上，本文考虑建筑物对基站信号的遮蔽影响，基于单兵前往灾区勘测的回传信息，提出了电力应急通信基站选址的双层优化方法。首先，根据灾区和电网公司的位置、单兵勘测路径，对研究问题进行了图形化描述。在此基础上，建立了基站选址的双层优化模型，上层以基站间信号传输路径上的损耗最小为目标，在基站可选位置范围内，对非线性模型利用粒子群算法(Partical Swarm Optimization, PSO)优化基站的预选位置；下层以基站间信号传输路径与建筑物的间隔距离最大为目标，利用支持向量机(Support Vector Machine, SVM)求解基站的最终位置，并传递回上层，计算信号传输损耗，通过迭代优化获得基站最优部署位置。通过与提出的单层模型的比较，验证了所提模型的有效性，可为发生重大自然灾害后电力应急通信网的搭建提供有益参考。

1 电力应急通信基站选址图形化描述

重大自然灾害导致某地的电力及通信网络中断，单兵携带卫星通信设备从电网应急指挥中心前往灾区查看电力设施受损情况，并同时勘测沿途通信网络状况，为基站部署提供辅助信息。

定义“前线基站”与“后方基站”，前线基站完成对抢修区域的信号覆盖，后方基站接入公共通信网，两基站采用定向天线实现信息交互。

电力应急通信基站选址的场景示意图如图1所示，将电力抢修区域用圆形覆盖，圆心为，半径为；前线基站若要覆盖此圆，则其与点的距离应满足式(1)。

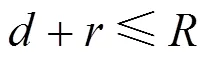
式中，R为前线基站的信号覆盖半径[17-18]。O点为单兵进入电力受灾区域，根据设备受灾情况以及抢修工作经验，在确定抢修作业地点后，利用卫星通信设备传回的位置。图1左侧阴影圆形为前线基站的可选位置区域，上式取等号时，抢修区域内圆与前线基站覆盖范围外圆内切。

后方基站需部署在存在公共通信网络的位置，但考虑到电力抢修对于时间快速性要求较高，不适合对全地图进行大范围勘探以确定公共通信网络良好与中断的位置边界，所以本文通过以下方式划定后方基站的可选位置区域。

单兵从指挥中心出发，行程的前半段存在公共通信网络；到达图1中点时通信网络中断，单兵通过卫星通信方式向指挥中心传回当前位置坐标；为使后方基站接入网络状态良好的公共通信网，将线段延长距离至；以为圆心，为半径，并辅以圆的平行切线，作弧；将弧右侧阴影区域作为后方基站的可选位置区域。

同时，从图1中可以看出，在前线基站、后方基站的可选位置区域内分别任意选定一点，两点连线与弧、弧各有一交点，两交点确定的线段与前一线段相比，距离更短，线段上建筑物更少，因此，信号受遮挡产生的损耗更小。

进而，将前线基站、后方基站的可选位置范围由阴影区域缩小为区域边界，即弧及。通过选定前线基站和后方基站的最优位置，使基站间信号传输路径的损耗最小，实现灾区内、外工作人员在较高信号强度下跨区域传送信息，这是本文要解决的关键问题。

2 电力应急通信基站选址双层优化模型

2.1 双层优化模型结构

本文以最小化信号传输路径的损耗为目标来优选基站位置，对于基站间信号传输路径的获得，考虑到传输路径上越通畅，建筑物越少，则信号的传输损耗越小，因此以主动避开建筑物为出发点，利用建筑物的分布信息，以传输路径与建筑物的间隔距离最大为目标生成信号传输路径。

为此，建立了电力应急通信基站选址的双层优化模型，其结构如图2所示。

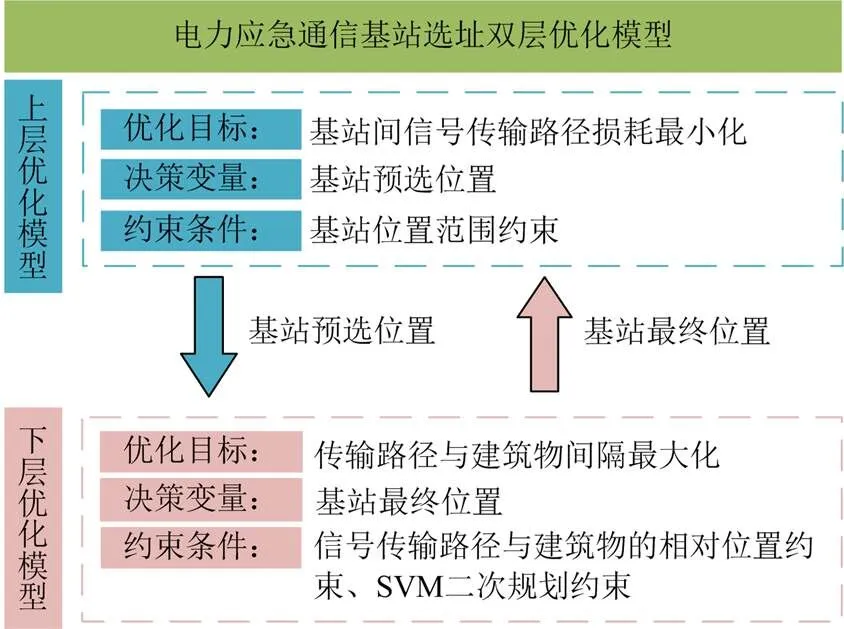
图2 双层优化模型结构

上层模型以信号传输路径的损耗最小化为目标，在基站可选位置范围内，优化基站的预选位置，并传入下层；下层模型以信号传输路径与建筑物的间隔距离最大化为目标，优化基站的最终位置，并传递回上层，计算信号传输损耗，通过迭代优化，获得基站的最优位置。

2.2 上层预选基站位置模型

基于前线、后方基站的可选位置范围以及建筑物位置、高度数据，建立应急基站选址的上层模型。

目标函数为

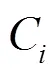
图3 绕射损耗求解示意图

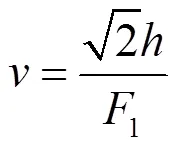
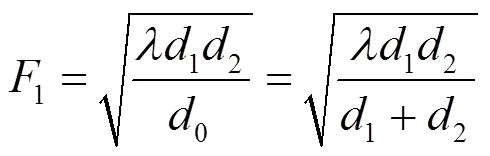
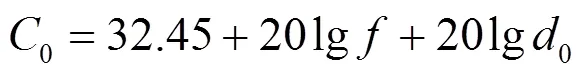
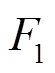
1) 位置范围约束

2) 信号传输损耗约束

基站信号发射功率与允许的最小信号接收强度的差值为最大信号传输损耗，为满足正常通信需求，基站位置的选取还应该满足式(9)所示的信号传输损耗约束。

2.3 基于SVM的信号传输路径下层模型

上层模型中考虑建筑物占地轮廓以及高度来计算信号传输损耗；在求取信号传输路径时，为使下层模型中解的物理意义与信号传输路径相符，将建筑物凝聚为二维平面中一点，以信号传输路径与建筑物的间隔最大作为目标，建立信号传输路径的下层优化模型。

信号传输路径与建筑物的间隔如式(10)所示。

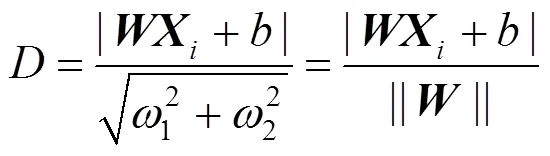
对于最大间隔距离的优化，本文引入了SVM。SVM是以统计学习理论为基础的数据挖掘方法[22-24]，可处理回归、模式识别(分类问题、判别分析)等诸多问题，其机理是寻找一个满足分类要求的最优分类超平面，使得超平面在保证分类精度的同时，超平面两侧空白区域最大化。当SVM应用到线性可分以及近似线性可分的二维数据分类中时，超平面为直线，空白区域最大化即数据点与直线的距离最大。可见，最优超平面与下层模型所要求解的信号传输路径有较大相似性，故本文基于SVM建立了信号传输路径的下层优化模型。以式(10)间隔距离最大为目标，并参考SVM的数学推导，则式(10)可转化为如下所述的凸二次规划问题。

目标函数为

约束条件1为

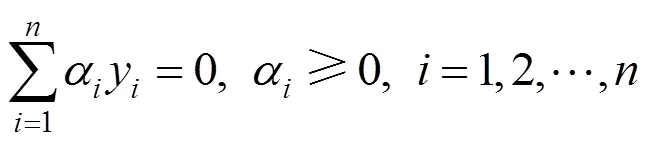
约束条件2为

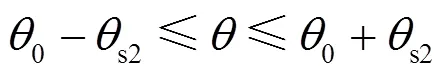
式中：θ为建筑物在极坐标系的角度；将前线、后方基站视为整体，对其形成的信号传输路径优化，为上层模型传入的信号传输路径预选位置，即图4中为前线基站预选位置，为后方基站预选位置。、为本文定义的角度常数；由于SVM最优超平面的确定仅与作为“支持向量”的建筑物数据点有关，故可缩小参与下层模型计算的建筑物范围，因此设置此约束条件，即图4中仅多边形PQNM里被虚线包围的建筑物参与下层模型求解。

约束条件3为

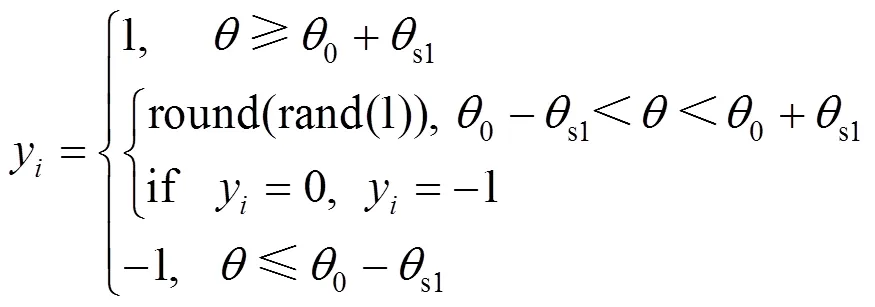
由式(11)—式(14)求得拉格朗日乘数以及支持向量后，和可由式(15)得到，即求得信号传输路径最终位置，然后将最终位置传入上层模型进行后续优化。

式中：为支持向量个数；用任意一个支持向量均可求得。

3 模型求解

对于上层模型非线性问题，采用智能优化算法PSO求解；下层的信号传输路径模型结合SVM建立，采用SVM求解；双层模型求解流程如图5所示，具体求解步骤如下所述。

1) 应急指挥中心接收单兵勘测过程中传回的坐标点，并读取坐标点周边一定范围内的建筑物位置及高度数据；

3) 设置上层模型粒子群求解算法的各项参数，如个体学习因子、群体学习因子、惯性权重、迭代次数、种群规模和粒子维度；

4) 依据步骤2)中基站的可选位置范围约束设置粒子群算法中各个粒子的位置搜索边界，即位置上下限，进而设置粒子的速度上下限；

8) 利用支持向量机求解下层模型的二次规划问题，并利用求解得到的拉格朗日乘数及支持向量计算信号传输路径最终位置，即得到最终位置对应的参数和，然后将此位置传入上层模型；

9) 上层模型根据下层模型传入的信号传输路径的最终位置计算传输损耗；

10) 根据传输损耗值的优劣来更新粒子群的个体最优值、群体最优值；

11) 比较迭代次数，判断粒子群算法是否迭代完成，若迭代完成，进入步骤13)，否则进入步骤12)；

12) 更新粒子位置，即信号传输路径预选位置，并且更新粒子速度，然后进入步骤7)；

13) 迭代完成，输出基站最优位置。

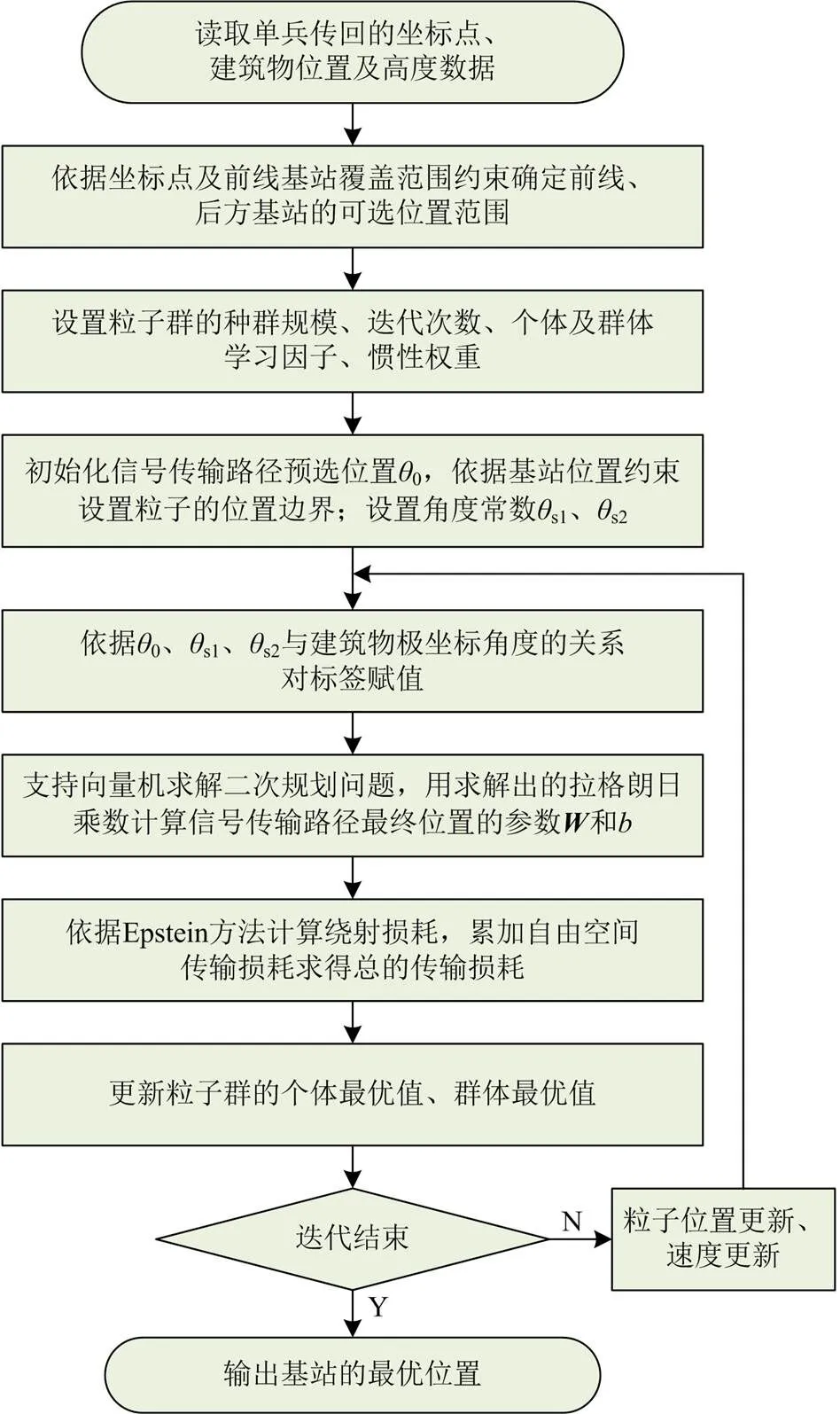
图5 求解流程示意图

4 算例分析

4.1 算例参数

在一定位置范围内，建筑物的基底面积总和与规划建设用地面积之比为建筑密度，目前我国城市建筑密度[25-26]一般不会超过40%～50%，算例设置城市的建筑密度为45.14%，即建筑物基底面积总和与规划建设用地面积的比值为45.14%。

建筑物的位置和高度数据利用随机函数生成，生成的建筑物的分布情况见图6。

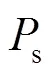
图6 建筑物分布示意图

用于求解上层模型的粒子群算法的参数见表1所示。

表1 粒子群算法参数

4.2 求解结果

PSO算法每次迭代中，粒子位置(即基站预选位置)被传入下层模型，下层优化得到的基站最终位置被传入上层以计算目标函数值，并更新粒子位置；算法迭代求得全局最优解(即基站最优位置)时，基站的最优位置为一组数据，即前线基站位置坐标与后方基站位置坐标；下层SVM优化算法使得基站最优位置存在对应不同最优预选位置的可能性。

记录了7个粒子在50次迭代过程中总共350对粒子预选位置及目标函数值的数据，通过与最优目标函数值的比对，找出了各个粒子在哪一代搜索到最优预选位置，其数据在表2中列出；其中粒子1与粒子2分别在不同代数收敛到了同一预选位置。此外，经过验证，增大迭代次数时，7个粒子均会搜索到最优预选位置，并且经过SVM的优化后得到同一基站最优位置。

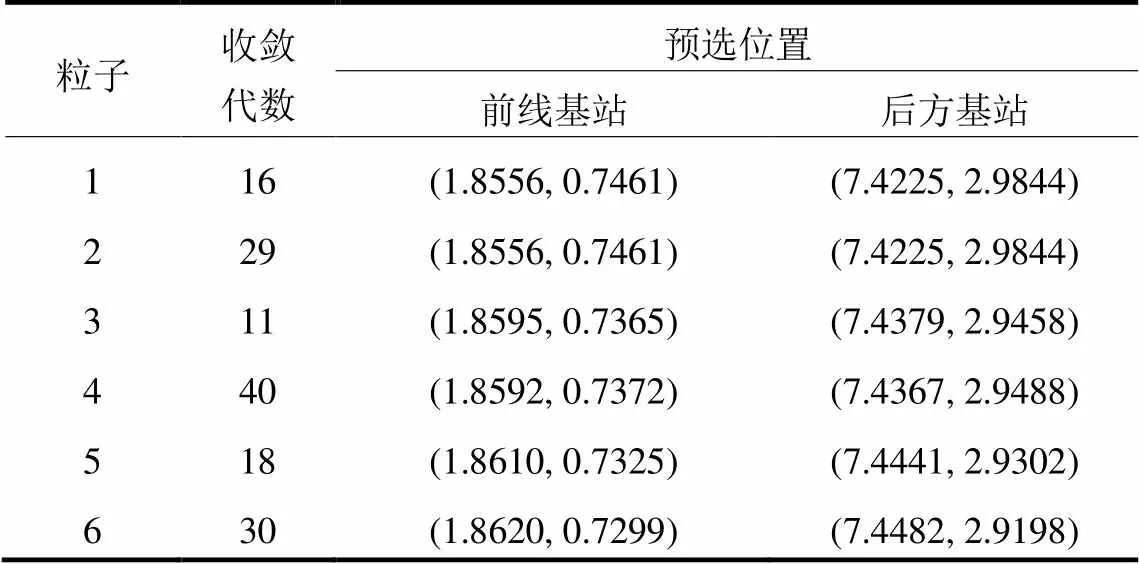
表2 预选位置数据

上层模型依据下层传回的基站最终位置计算传输损耗，粒子群最小传输损耗在迭代过程中的变化情况如图7所示。

图7 双层模型最小损耗变化过程

下层模型依据表2预选位置数据求得了基站最优位置，其位置坐标以及信号传输路径位置参数、信号传输损耗如表3所示。

表3 双层模型最优位置数据

表2中基站预选位置以及表3中基站最优位置对比如图8所示。

图8 预选位置与最优位置对比示意图

由图8可以看出，在基站预选位置基础上，下层模型对基站位置作了进一步优化，使得双层模型的整体求解算法在基站可选位置范围内进行了全局的寻优。

4.3 模型及算法比较

依据本文第1节对电力应急通信基站选址问题的图形化描述，本文除提出双层模型之外，还思考了如何利用单层模型求解基站最优位置，下面对其进行简单介绍，并与双层模型从模型本身与求解方法两方面来进行比较。

模型本身方面，单层模型为双层模型中的上层模型，如式(2)—式(8)所示。

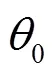
除上述差异外，算例仿真中建筑物分布、信号传输损耗计算方法相同，粒子群算法中的个体学习因子、群体学习因子、粒子位置上下限、速度上下限、种群规模也相同。

下面为单层模型的求解结果，粒子的群体最小信号传输损耗在迭代过程中的变化情况如图9所示。

图9 单层模型最小损耗变化过程

迭代结束后，基站最优位置的数据见表4，其中包括前线基站坐标、后方基站坐标、传输损耗最小值。

表4 单层模型最优位置数据

同时，为与图8中双层模型得到的基站最优位置作直观的比较，将表4中前线基站和后方基站的位置也绘制在图中，基站位置如图10所示。

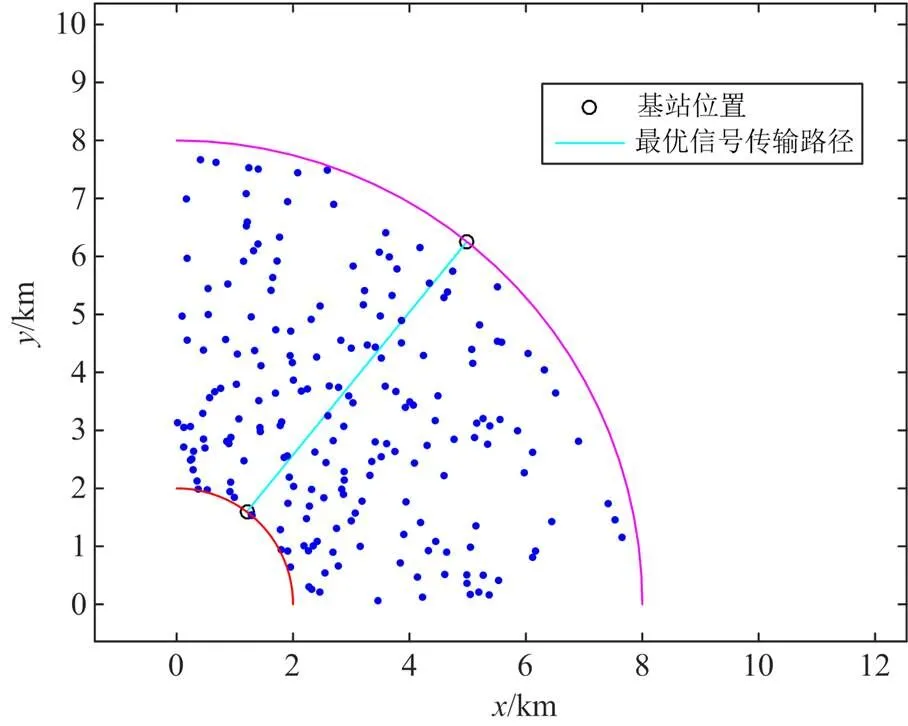
图10 单层模型基站最优位置

对比图7中双层模型最小损耗变化过程和图9中单层模型最小损耗变化过程，可以看出，双层模型用更少的迭代次数求得了更优的损耗数值，原因在于双层模型中支持向量机对上层模型输入的基站位置作了进一步优化，使得在每一次的迭代中信号传输路径的损耗进一步减小。

此外，单层模型求解过程中粒子群算法的初始基站位置随机给定，对于不同的基站位置初始值，所得出的最优基站位置存在差异，最小损耗数值相差大约10～20 dB，其中损耗最优值为105 dB左右，与双层模型获得的105.3845 dB相差甚小，但是鉴于单层模型受初始位置影响较大，结果随机性较高，对于求解最优值的性能不够稳定。因此，本文进行了多次实验，最终选择了单层模型中出现次数最多的数值结果与双层模型进行比较，同时，这也反映出双层模型比单层模型具有更好的稳定性，求解结果受基站初始给定位置的影响更小。

总的来说，单层与双层模型的对比实验证明了双层模型的有效性、稳定性，可为电力应急通信网络搭建过程中应急基站的部署提供参考。

4.4 基站最优位置影响因素分析

相比于正常情景下通信基站选址原则中对于地质条件、市电引入方式便捷与否、临近设备信号干扰强度大小等因素的要求，电力应急抢修情景下，车载通信基站由于其应用场景特殊性、自备发电机、移动灵活性、部署便捷性、工作周期短的特点，基本不受前述选址原则的影响，所以本文着重以增大信号传输距离、提升信号质量为导向，以前线、后方基站间信号传输损耗最小为目标建立数学模型，并由此计及影响信号传输损耗的建筑物遮蔽因素。

建筑物在二维空间分布上具有疏密特征，在三维空间分布上还具有高矮特征。在本文双层模型中，下层将建筑物凝聚为平面中一点，通过优化计算为上层传递回间隔最大、邻近建筑物较“疏”的信号传输路径，但并未考虑建筑物高度因素；上层纳入了建筑物高度以及占地范围来计算信号绕射损耗，通过迭代计算优化出损耗最小的信号传输路径。

通过分析可以得出，假如灾区内建筑物高度差距不大，最优传输路径会穿过建筑物排布较稀疏的区域；如果建筑物排布均匀，最优传输路径会穿过建筑物高度偏低的地区；考虑更一般的情况，如果某个地区建筑物没有明显的疏密和高矮特征，正如本文算例利用随机函数生成的建筑物位置、高度数据所示，所提模型会朝着建筑物分布较疏、高度较低的方向选取最优传输路径。

电网部门除了依靠单兵回传的信息外，还可以主动联络灾区外的附属单位以及城市相关部门，确定其他通信网络状况良好的地区，以增大基站位置的可选范围。

5 结论

为加快电力应急通信网络的搭建，保障电网抢修工作的后续开展，本文考虑建筑物对基站信号的遮蔽影响，基于单兵前往灾区勘测的回传信息，提出电力应急通信基站选址的双层优化方法。在对研究问题进行图形化描述的基础上，建立应急基站选址的双层优化模型，模型采用粒子群算法与支持向量机求解，通过迭代优化求得基站最优部署位置；此外，通过与本文提出的单层模型的对比分析，得出以下结论：

1) 考虑建筑物疏密分布的下层模型在计及上层模型信号传输损耗的基础上，对基站位置作了进一步优化调整，使得算法求解初期便得到较小的信号损耗数值，并且迭代次数更少。

2) 粒子群算法求解单层模型受基站初始位置影响较大，最优值也与双层模型有一定差距；经过多次实验，发现本文双层模型更具求解稳定性以及结果更优性。

3) 部署跨区域通信的应急基站时，与依靠人的经验部署基站相比，数学建模的方法可以减少因人员尝试并不断调整基站位置所花费的时间，提高电力抢修效率，减少停电时间。

在应急状态下的电网抢修过程中，本文所提方法可为电网部门部署应急基站提供系统化参考方案，加快电力应急通信网络搭建进程。本文利用无线基站搭建通信网络，关于建设电力应急通信网的后续研究也可考虑引入其他通信方式，搭建多种通信方式并存的应急通信网络。

[1] 严道波, 文劲宇, 杜治, 等. 2021年得州大停电事故分析及其对电网规划管理的启示[J]. 电力系统保护与控制, 2021, 49(9): 121-128.

YAN Daobo, WEN Jinyu, DU Zhi, et al. Analysis of Texas blackout in 2021 and its enlightenment to power system planning management[J]. Power System Protection and Control, 2021, 49(9): 121-128.

[2] 王群, 李巍, 于海, 等. 基于模糊层次分析法的评估方法在电力系统应急通信预案中的应用研究[J]. 电力系统保护与控制, 2018, 46(22): 171-177.

WANG Qun, LI Wei, YU Hai, et al. Research on the application of evaluation method based on fuzzy analytic hierarchy process in emergency communication plans for power system[J]. Power System Protection and Control, 2018, 46(22): 171-177.

[3] 张英杰, 毛赐平, 俎云霄, 等. 基于免疫算法的TD- SCDMA网络基站选址优化[J]. 通信学报, 2014, 35(5): 44-48.

ZHANG Yingjie, MAO Ciping, ZU Yunxiao, et al. Immune algorithm-based base station location optimization in the TD-SCDMA network[J]. Journal on Communications, 2014, 35(5): 44-48.

[4] 朱思峰, 陈国强, 张新刚, 等. 多目标优化量子免疫算法求解基站选址问题[J]. 华中科技大学学报(自然科学版), 2012, 40(1): 49-53.

ZHU Sifeng, CHEN Guoqiang, ZHANG Xingang, et al. Multi-objective optimization quantum immune algorithm for solving base stations location planning problem[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(1): 49-53.

[5] 金伟正, 宋超, 罗义军. 基于人工鱼群算法的电力无线专网基站选址规划[J]. 武汉大学学报(工学版), 2021, 54(6): 551-556.

JIN Weizheng, SONG Chao, LUO Yijun. Base station location planning of power wireless private network based on artificial fish swarm algorithm[J]. Engineering Journal of Wuhan University, 2021, 54(6): 551-556.

[6] CHRISTODOULOS S, CONSTANTINOS P, IOANNIS K. Low-complexity base station selection scheme in mmwave cellular networks[J]. IEEE Transactions on Communications, 2017, 65(9): 4049-4064.

[7] MA Jianpeng, ZHANG Shun, LI Hongyan, et al. Base station selection for massive MIMO networks with two-stage precoding[J]. IEEE Wireless Communications Letters, 2017, 6(5): 598-601.

[8] 马宝罗, 贾振红, 覃锡忠, 等. 改进免疫算法在无线网络基站选址优化中的应用[J]. 传感器与微系统, 2016, 35(5): 154-157.

MA Baoluo, JIA Zhenhong, QIN Xizhong, et al. Application of improved immune algorithm in wireless network base station location planning optimization[J]. Transducer and Microsystem Technologies, 2016, 35(5): 154-157.

[9] 邓创. 基于无线自组网的电力应急现场指挥通信系统[J]. 电力信息与通信技术, 2015, 13(5): 67-72.

DENG Chuang. A power system emergency communication system based on MANET[J]. Electric Power Information and Communication Technology, 2015, 13(5): 67-72.

[10]肖炳林. 应急通信在电力抢修中的应用[J]. 数字通信世界, 2018(8): 204, 233.

[11]胡红明. 突发事件下电网通信应急技术探讨[J]. 贵州电力技术, 2014, 17(5): 58-59, 78.

HU Hongming. Discussion on the emergency technology in power grid communication[J]. Guizhou Electric Power Technology, 2014, 17(5): 58-59, 78.

[12] KALYAN C H N S, SAMBASIVA R G. Impact of communication time delays on combined LFC and AVR of a multi-area hybrid system with IPFC-RFBs coordinated control strategy[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 89-108.

[13]程紫运, 吕明卉, 田云飞, 等. 基于结构熵的电力骨干通信网抗毁性研究[J]. 电力系统保护与控制, 2020, 48(5): 112-118.

CHENG Ziyun, LÜ Minghui, TIAN Yunfei, et al. Research on invulnerability for electric power backbone communication network based on structural entropy[J]. Power System Protection and Control, 2020, 48(5): 112-118.

[14]胡青松, 杨维, 丁恩杰, 等. 煤矿应急救援通信技术的现状与趋势[J]. 通信学报, 2019, 40(5): 163-179.

HU Qingsong, YANG Wei, DING Enjie, et al. State-of- the-art and trend of emergency rescue communication technologies for coal mine[J]. Journal on Communications, 2019, 40(5): 163-179.

[15]黄国欢. 基于4G网络的电力移动应急指挥系统的设计与应用[D]. 广州: 华南理工大学, 2016.

HUANG Guohuan. Power grid mobile emergency command system based on 4G network[D]. Guangzhou: South China University of Technology, 2016.

[16]樊冰, 郑陈熹, 唐良瑞, 等. 基于多属性决策的电力通信网的节点重要度计算方法[J]. 电力系统保护与控制, 2020, 48(9): 68-76.

FAN Bing, ZHENG Chenxi, TANG Liangrui, et al. Node importance evaluation method of electric power communication network base on multi-attributes decision making[J]. Power System Protection and Control, 2020, 48(9): 68-76.

[17]陈龙, 刘宇明, 陈文. 电力应急通信中覆盖范围研究[J]. 云南电力技术, 2016, 44(5): 69-71.

CHEN Long, LIU Yuming, CHEN Wen. Research on coverage of TD-LTE in electric power emergency communication[J]. Yunnan Electric Power, 2016, 44(5): 69-71.

[18]黄芷辛, 冯健, 麦磊鑫. LTE链路预算研究及分析[J]. 移动通信, 2013, 37(8): 45-50.

HUANG Zhixin, FENG Jian, MAI Leixin. LTE link budget study and analysis[J]. Mobile Communications, 2013, 37(8): 45-50.

[19] Mehmet Barış TABAKCIOĞLU,Ahmet CANSIZ. Electromagnetic wave propagation models for multiple-diffraction scenarios[J]. Uludağ University Journal of The Faculty of Engineering, 2014, 19(1).

[20] 刘利强, 宋志群, 陈大勇. 山区通信中单刃峰绕射损耗的工程化近似模型[J]. 无线电通信技术, 2015, 41(1): 24-27.

LIU Liqiang, SONG Zhiqun, CHEN Dayong. Engineering approximate model of single knife-edge diffraction loss in mountainous communication[J]. Radio Communications Technology, 2015, 41(1): 24-27.

[21] 邹高翔, 童创明, 王童, 等. 空间与地面菲涅尔区的特性研究[J]. 弹箭与制导学报, 2017, 37(1): 129-134.

ZOU Gaoxiang, TONG Chuangming, WANG Tong, et al. Studies on the characteristics of the space fresnel zone and the ground fresnel zone[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2017, 37(1): 129-134.

[22]杨天琦, 王琦, 叶志浩. 基于迁移支持向量机的舰船综合电力系统继电保护方法研究[J]. 电力系统保护与控制, 2020, 48(23): 124-132.

YANG Tianqi, WANG Qi, YE Zhihao. Research on relay protection of ship integrated power system based on transfer support vector machine[J]. Power System Protection and Control, 2020, 48(23): 124-132.

[23]戴远航, 陈磊, 张玮灵, 等. 基于多支持向量机综合的电力系统暂态稳定评估[J]. 中国电机工程学报, 2016, 36(5): 1173-1180.

DAI Yuanhang, CHEN Lei, ZHANG Weiling, et al. Power system transient stability assessment based on multi-support vector machines[J]. Proceedings of the CSEE, 2016, 36(5): 1173-1180.

[24] 刘敬, 谷利泽, 钮心忻, 等. 基于单分类支持向量机和主动学习的网络异常检测研究[J]. 通信学报, 2015, 36(11): 136-146.

LIU Jing, GU Lize, NIU Xinxin, et al. Research on network anomaly detection based on one-class SVM and active learning[J]. Journal on Communications, 2015, 36(11): 136-146.

[25]李和平, 刘志. 中国城市密度时空演变与高密度发展分析—从1981年到2014年[J]. 城市发展研究, 2019, 26(4): 46-54.

LI Heping, LIU Zhi. Temporal and spatial evolution of urban density in China and analysis of urban high density development: from 1981 to 2014[J]. Urban Development Studies, 2019, 26(4): 46-54.

[26]葛亚宁, 徐新良, 李静, 等. 北京城市建筑密度分布对热岛效应的影响研究[J]. 地球信息科学学报, 2016, 18(12): 1698-1706.

GE Yaning, XU Xinliang, LI Jing, et al. Study on the influence of urban building density on the heat island effect in Beijing[J]. Journal of Geo-information Science, 2016, 18(12): 1698-1706.

Two-layer optimization method for site selection of a power emergency communication base station considering building shadowing effect

WANG Zhiqiang, DONG Zhongtao, WANG Xiaolong, LIU Wenxia, MAO Yuyang, HUANG Yijuncheng

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources,(North China Electric Power University), Beijing 102206, China)

There are shortcomings in the deployment of power emergency communication base stations that only rely on human subjective experience. Therefore, considering the influence of buildings on the shielding of base station signals, the research problems are graphically described based on the return information of individual soldiers to the disaster area. In addition, a two-layer optimization model for the location of power emergency communication base stations is proposed. The upper layer model aims to minimize the signal transmission loss between base stations. Within the delineated optional location range of base stations, the particle swarm algorithm is used to optimize the pre-selection of base stations for the nonlinear model. The lower layer model aims to maximize the distance between the signal transmission path and the building. A support vector machine is used to optimize the final position of the base station, and this is transmitted back to the upper layer to calculate the signal transmission loss. The optimal deployment position of the base station is obtained through iterative optimization. The feasibility and effectiveness of the proposed method are verified by comparing with the single-layer model in an example. The work can provide a technical reference for the construction of a power emergency communication network after major natural disasters.

power emergency communication base station; cross-region deployment; building shadowing effect; signal transmission loss; two-layer optimization; particle swarm optimization; support vector machine

10.19783/j.cnki.pspc.211675

国家重大科技专项资助(2020YFC0827001)

This work is supported by the National Science and Technology Major Project of China (No. 2020YFC0827001).

2021-12-09；

2022-04-26

王志强(1967—)，男，副教授，硕士生导师，研究方向为电力系统运行控制、电力系统继电保护等；E-mail: wwwgode@163.com

刘文霞(1967—)，女，教授，博士生导师，研究方向为电力系统规划与可靠性、电力系统风险评估等；E-mail: liuwenxia001@163.com

董忠涛(1996—)，男，通信作者，硕士研究生，研究方向为电力应急与电力系统恢复。E-mail: 17853266603@ 163.com

(编辑 魏小丽)