含深度学习代理模型的有源配电网电压无功控制进化算法

潘思蓉，刘友波，唐志远，张 曦，祁浩南，刘俊勇

含深度学习代理模型的有源配电网电压无功控制进化算法

潘思蓉，刘友波，唐志远，张 曦，祁浩南，刘俊勇

(四川大学电气工程学院，四川 成都 610065)

分布式可再生能源的大规模接入，加剧了有源配电网(Active Distribution Network, ADN)的三相不平衡，容易导致系统电压越限与线损增加。然而，由于当前配电网量测设备安装不全，部分节点负荷数据难以准确获取，因此传统基于全局观测的ADN电压控制方法难以满足实际控制需求。为解决上述问题，提出一种含深度学习代理模型的电压无功控制(Volt/Var control, VVC)进化算法。设计以高速公路神经网络为代理模型，精确拟合局部量测负荷信息、调压控制策略与系统性能指标之间的映射关系。将训练后的代理模型嵌入非支配排序遗传算法的迭代寻优过程中，对电压偏移率、三相不平衡度及线路损耗指标进行直接计算，实现数据驱动的配电网VVC策略快速求取。在改进的IEEE 123节点三相配电网算例上进行测试，验证了所提算法的性能优势及求解效率。

有源配电网；三相不平衡；电压无功控制；高速公路神经网络；非支配排序遗传算法；辅助代理模型

0 引言

随着大规模可再生能源的非全相接入，有源配电网(Active Distribution Network, ADN)电压越限线路损耗问题愈发严重[1-2]，其固有的三相不平衡特征也更为突出[3-4]。而系统不平衡运行将引起电压负序分量激增，致使设备运行异常且损耗增大[5-7]。因而，考虑电压不平衡度的三相配电网优化控制方法具有一定的实际意义。此外，由于实际配电网系统中量测装置覆盖率较低[8-9]，部分不与调度主站相连的节点负荷数据无法被实时采集，只可在次日通过营销系统获取，致使基于全局信息的实时电压无功控制(Volt/Var control, VVC)优化方法难以奏效。因此，研究一种配电网VVC策略的快速求取技术显得尤为重要。

目前，针对可控资源逐渐多样化的配电网三相不平衡模型，研究人员多采用动态规划[10]、序列二次规划[11]及Benders分解法[12]等进行求解。然而，文献[10-12]所述方法需实时获取配电网全局节点数据，无法适用于非全实时观测的配电网当中。因次，有学者提出以传统智能算法弥补上述不足，将细菌趋药性算法[13]、遗传算法[14]与差分进化算法[15]等运用到量测不足电网的系统状态估计与设备优化配置等领域，提高模型的适应能力。而此类算法的计算效率易随问题维数增高而下降，难以满足快速计算要求。

近年来，为降低高维非线性模型的求解难度，人们逐渐对代理辅助方法展开研究，包含多项式回归[16]、径向基函数[17]、克里格[18]及神经网络[19]等多种建模方式。其中，深度神经网络(Deep Neural Network, DNN) 已被证实为一种成功的代理辅助方法[19]，其在无功优化领域的研究也在逐步展开。文献[20]采用深度卷积神经网络，对VVC模型中系统注入功率与关键节点电压之间的规则进行挖掘。文献[21]基于深度置信网络，映射系统无功电压特征与优化策略之间的关系。文献[22]通过深层图卷积架构反映电力设备状态与负荷数据之间的规则，实现节点电压控制。上述文献虽可提升算法性能，却未考虑三相不平衡问题的优化方式。此外，传统DNN的收敛性能易受“梯度弥散”问题影响[23]，难以适应控制目标日益复杂的高维VVC模型，因此，亟需采取性能更优的神经网络结构。

针对上述问题，本文提出含深度学习代理模型的电压无功优化控制进化方法。首先，离线构建基于高速公路神经网络(Highway Networks, HWN)的非全观测条件下系统性能指标评估代理模型，其网络结构较传统DNN拥有更深规模[24]，可学习局部数据与全局特征之间的更深层内在规律，用以拟合可观测节点负荷信息、调压设备控制策略与性能指标之间的映射关系，拥有收敛能力强、泛化性好的优点。其次，区别于传统进化算法的耗时求解过程，所提算法将代理模型嵌入非支配排序遗传算法(NSGA-II)的迭代寻优过程中，可对包含节点电压偏移率、线路损耗及局部母线电压不平衡度在内的适应度指标进行直接计算，由此形成VVC策略的数据驱动快速求取技术。本文所提方法在改进的IEEE 123节点仿真模型上进行测试，验证了所提算法的优越性和适用性。

1 三相配电网电压无功控制模型

综合考虑步进电压调节器(Step Voltage Regulator, SVR)、分组投切电容器(Capacitor Banks, CBs)、静态无功补偿器(Static Var Compensator, SVC)、单相光伏设备(PV)及三相分布式储能系统(Distributed Energy Storage System, DESS)之间的互补协调能力，建立三相不平衡配电网VVC模型。

1.1 目标函数

设定以下3项系统性能指标。

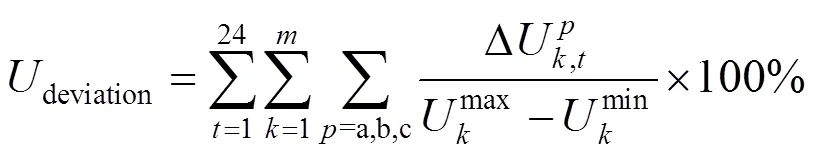
2) 线路损耗loss,t

首先计算等效电流e，如式(2)所示。

相应线损计算为

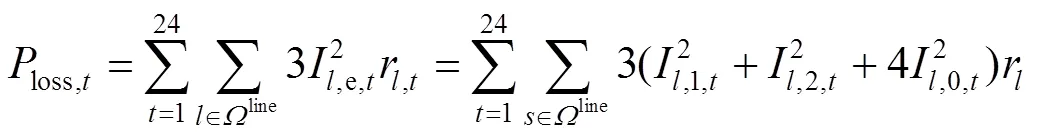
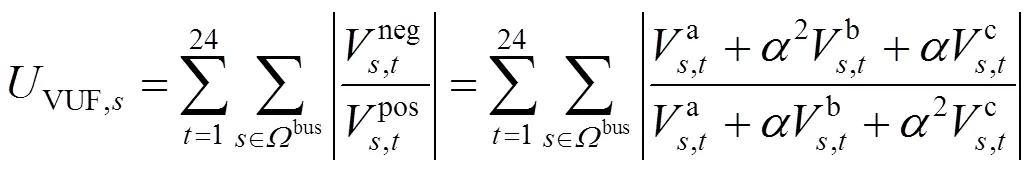
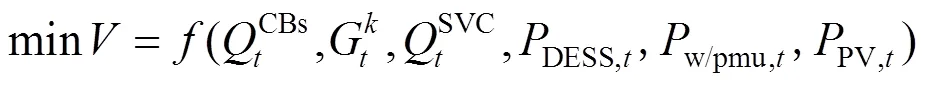
1.2 系统约束条件

1) 功率平衡约束

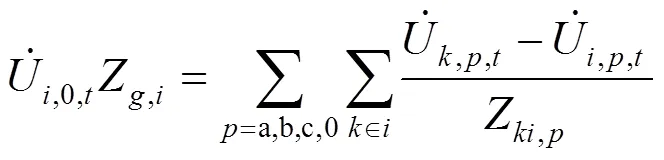
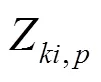
2) DESS运行约束

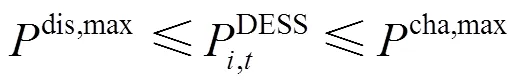
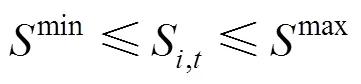
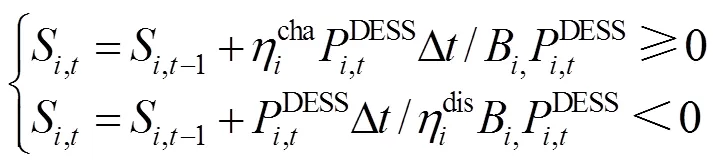
3) SVR运行约束

4) CBs投切约束

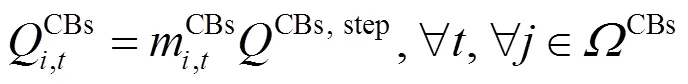
5) SVC运行约束

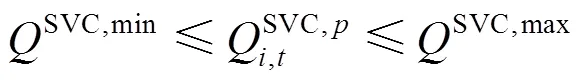
2 高速公路神经网络驱动的代理模型

非全观测配电网的电压无功控制框架，主要包括对优化模型的离线训练和在线计算两部分。离线训练部分主要包括建立离线样本数据库及构建神经网络代理模型。将通过高速公路神经网络(HWN)拟合局部负荷信息、调压设备策略与性能指标=[deviation,lossVUF]之间的隐式映射关系，以此作为系统指标的评估代理模型，简化多目标问题的求解难度。

2.1 离线样本数据库的构建

2.1.1样本输入数据集合

1) 历史负荷数据库。通过整合调度及营销系统的历史信息，获取配电网全局节点的历史负荷数据。

2) 拉丁超立方抽样方法与样本生成

拉丁超立方抽样(Latin Hypercube Sampling, LHS)是一种分层抽样技术[25-26]，与简单随机抽样(Simple Random Sampling, SRS)相比，其采样均匀度高，因此采用LHS可有效提高深度学习代理模型的泛化能力。利用LHS的样本生成步骤如下所述。

(1) 光伏-负荷场景

利用LHS生成个出力波动范围一定的光伏运行样本，将其与组全节点负荷样本组合，形成组光伏-负荷场景，考虑1.2节系统运行约束，使用粒子群算法进行各场景的无功优化。

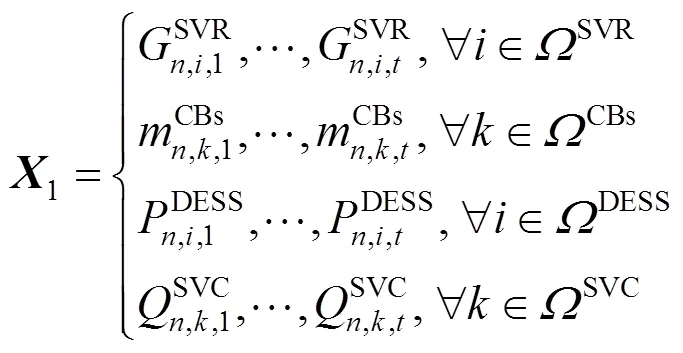
2.1.2样本标签数据集合

针对场景优化结果，由式(1)—式(4)计算各场景性能指标，以此作为组样本标签数据集合，即

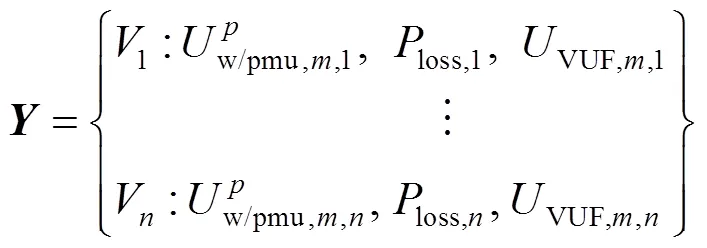
由此，HWN模型离线样本数据库如表1所示。

表1 高速公路神经网络模型离线样本数据库

2.2 高速公路神经网络

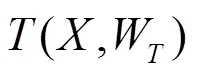
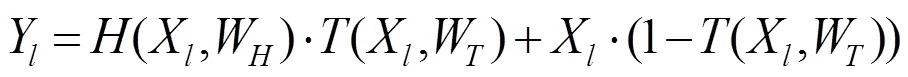
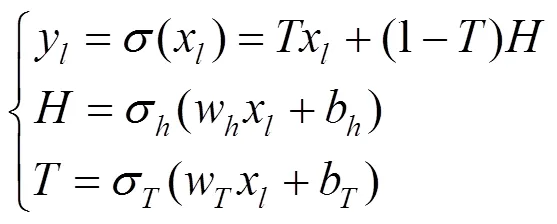
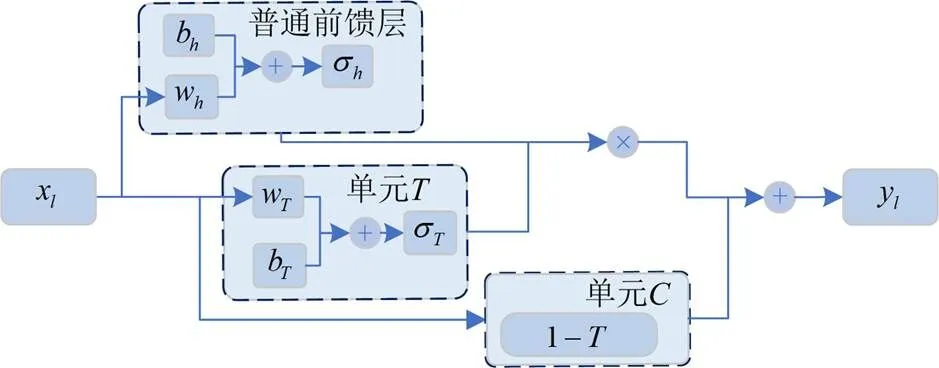
图1 高速公路神经网络结构图

显然，HWN基于普通DNN进行了结构改进，可通过的不同取值，自适应调节网络层数：当= 1时，HWN退化成普通网络结构；当= 0时，HWN将形成信息跨层直接传输的通道。因此，当隐层数目增加时，HWN可实现优于普通网络的收敛性能。

2.3 基于HWN的系统性能指标评估代理模型

由HWN学习模型样本的映射关系，离线构建系统性能指标评估代理模型，训练过程如图2所示。

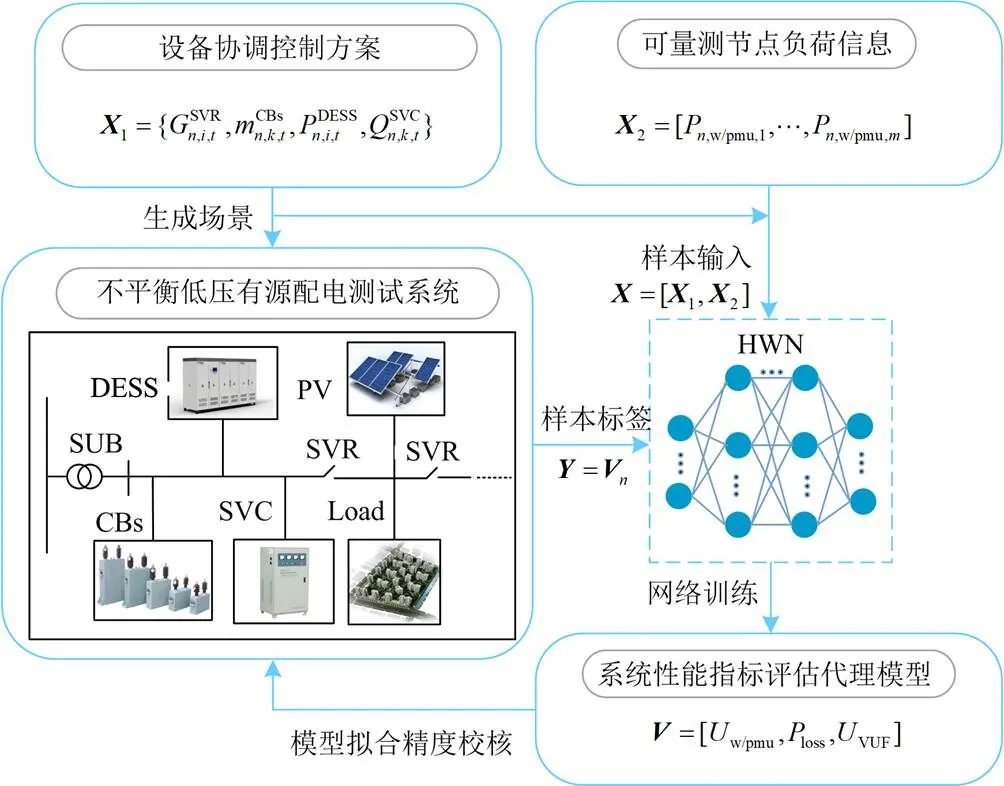
图2 基于HWN的系统性能指标评估代理模型

每日结束后收集该日运行数据，扩充离线样本数据库，对HWN模型进行更新训练。其中，以样本测试集校核训练效果，定义RMSE表示均方根误差(Root Mean Square Error, RMSE)、表示相关系数(coefficient of association)，作为模型训练评估指标。

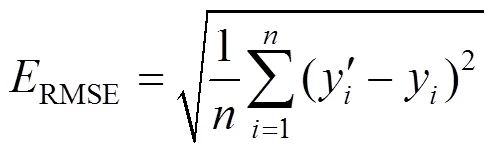
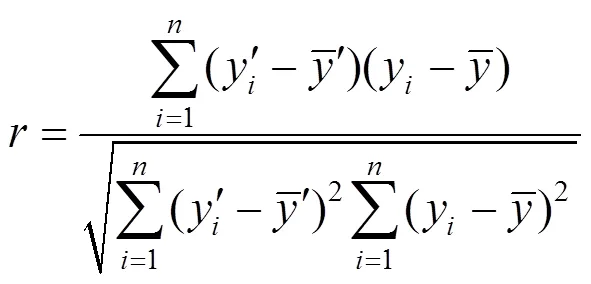
3 含深度学习模型的VVC策略进化算法

3.1 NSGA-II算法及其适应性改进

NSGA-II是高效求解多目标问题的优化算法[28-29]，本文以可观节点各相电压偏移率、线路损耗及局部母线电压三相不平衡度作为3项最小化目标。

3.2 HWN-NSGA-II算法框架

针对日内无功优化场景，通过量测设备实时采集可观测节点负荷信息，输入HWN代理模型后，将模型输出作为NSGA-II寻优过程中的适应度函数求取结果，进而快速获得算法VVC最优策略，构成HWN-NSGA-II计算框架，其流程如图3所示。

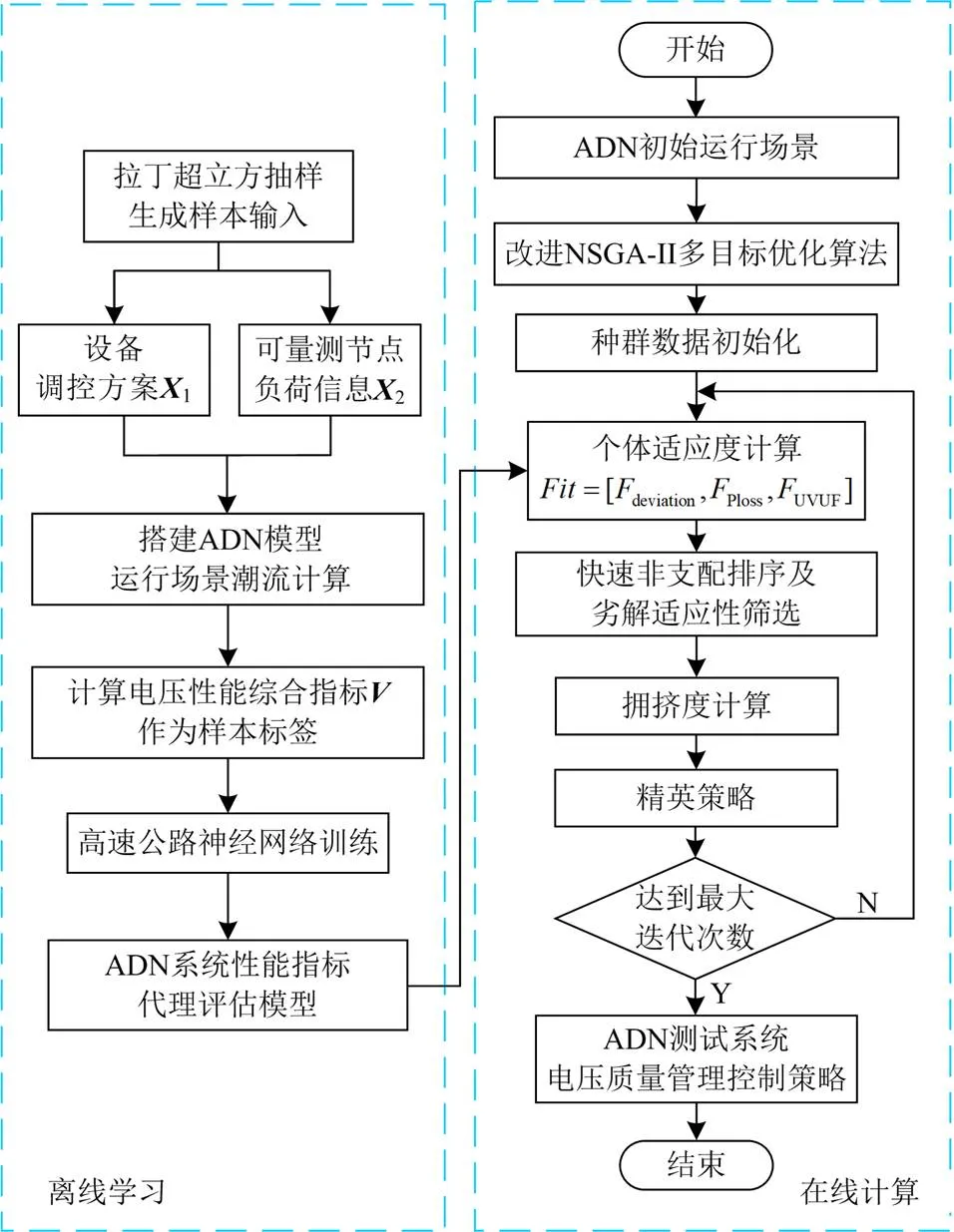
图3 HWN-NSGA-II算法框架

Fig. 3 Algorithm framework of HWN-NSGA-II

4 算例分析

4.1 测试系统网架结构

改进的IEEE 123节点配电网测试系统参数设置如下：峰值负荷调升至原系统的1.6倍，即5.584 MW。负荷组成为：48%恒功率负荷+40%恒阻抗负荷+12%恒电流负荷，将恒阻抗负荷设置为三相不平衡负荷，其三相有功与无功功率均值分别等同于该负荷平衡状态下的有功与无功功率数值。

表2 可控设备接入节点位置及相序

图4 日负荷与光伏出力曲线的对比图

表3 DESS配置参数

4.2 HWN评估代理模型性能分析

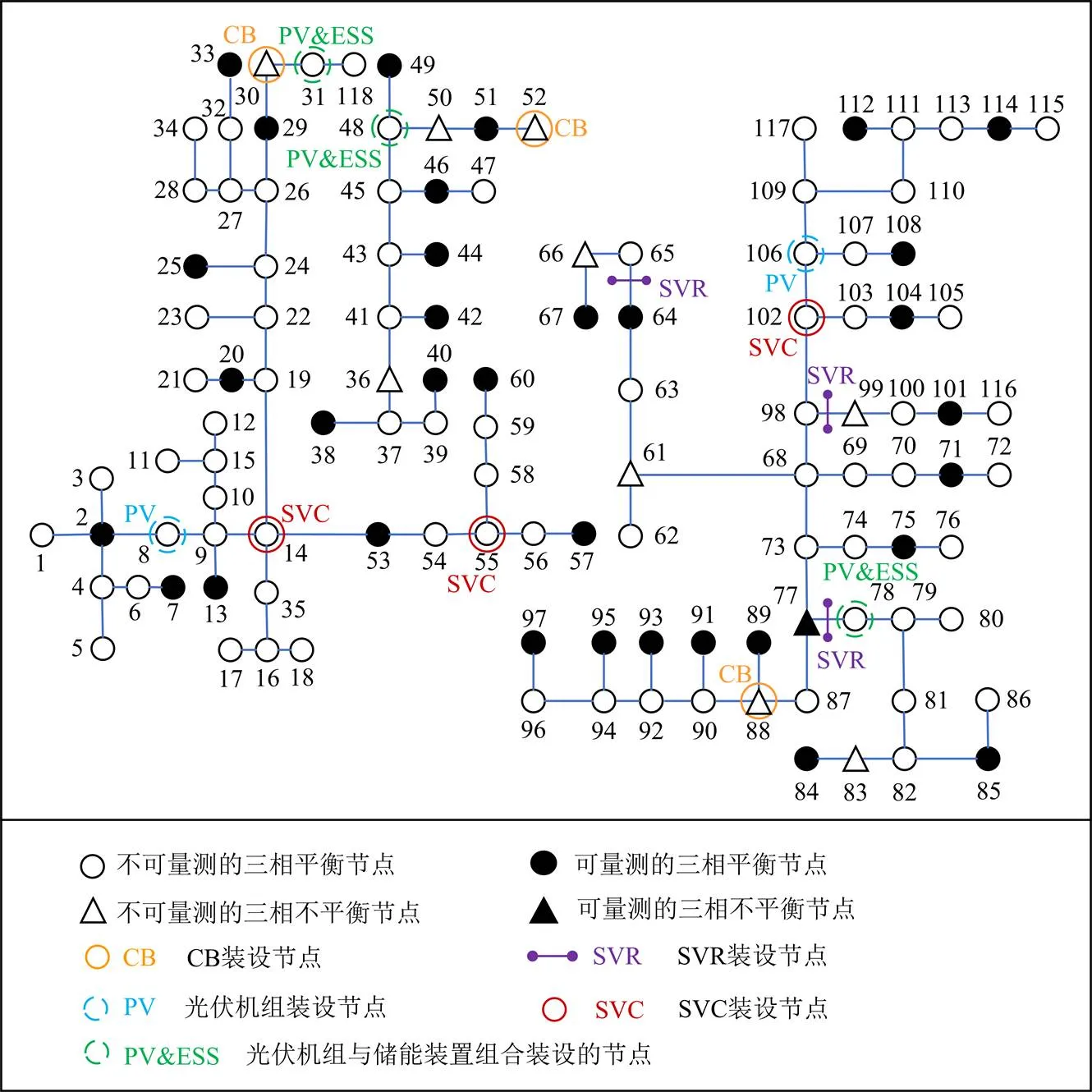
图5 改进的IEEE-123节点测试系统结构

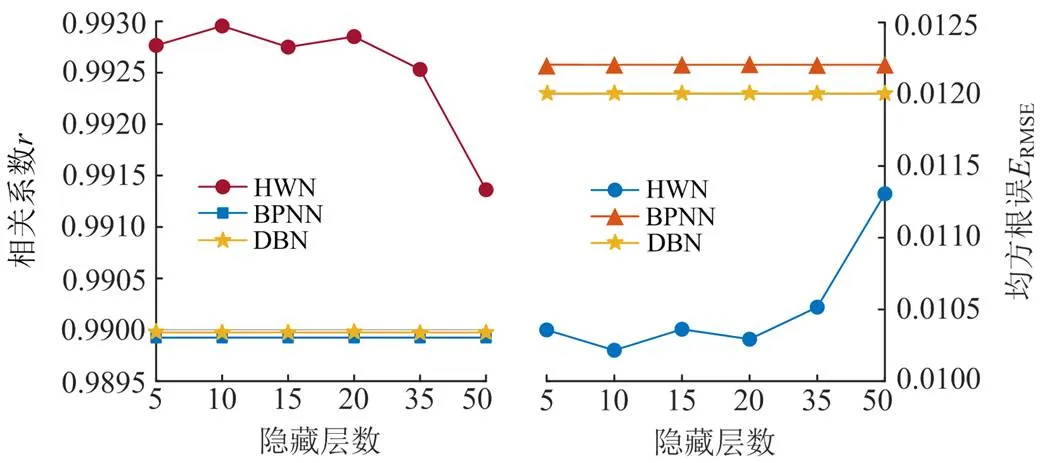
图6 神经网络训练拟合效果对比图

由表4可知：

表4 不同观测节点数设置下神经网络训练拟合效果对比

由此表明，HWN评估代理模型，可达到较普通DNN更高的优化精度，适合于较大规模配电参数的拟合应用，且在不同感知测试环境下，代理模型均可进行配网局部信息与全局指标的深度拟合，弥补了传统全信息优化方式的短处，为构建高准确度的非全实时观测在线计算框架奠定基础。

4.3 HWN-NSGA-II算法性能分析

选定相同训练参数，将HWN-NSGA-II代理辅助进化算法与基于网络全负荷信息的改进NSGA-II算法、基于基础潮流的多目标粒子群算法(Multi Objective Particle Swarm Optimization, MOPSO)[31]、遗传算法(GENETIC ALGORIThm, GA)[32]以及蚁群算法(Ant Colony Optimization, ACO)[33]进行对比，结果如表5所示。其中，deviation指标选取可观节点C相电压偏移率均值。

表5 各算法拟合结果及求解效率对比

由表5可知，所提HWN-NSGA-II算法具有优越的计算性能，具体体现在：(1) HWN-NSGA-II属于非完全观测计算方法，但其优化效果与全负荷信息算法(NSGA-II)相近，且其各指标优化效果均明显优于其余3种算法；(2) HWN-NSGA-II可在11 s内完成调压决策，具有最佳的计算效率。此效率优势主要得益于进化算法中代理模型的有效嵌套，使得在NSGA-II适应度函数迭代求取中，避免了频繁的潮流计算与目标求解，大幅降低了寻优时长，体现了所提算法的优越性。

4.4 电压无功优化控制结果分析

基于如图4所示负荷水平及PV出力已知的测试系统环境，经过HWN-NSGA-II算法决策调控后，VVC模型中可控设备的分布情况分别如下所述。

1) CBs与SVR设备

如图7所示，CBs、SVR均满足设备运行约束，主要在11：00—20：00净负荷大幅波动时段进行调节操作。CBs通过提供无功补偿，实时维持电压水平；SVR通过调节分接头位置，平稳线路末端电压。由于SVR分接头位置主要在3—8间切换，因此若系统潮流分布突变，其仍具备一定的电压调节裕度。

2) SVC设备

如图8所示，SVC可在负荷需求高峰期，快速输出容性补偿功率，从而有效进行负荷跟踪。

3) DESS设备

如图9所示，DESS在负荷峰值期放电对节点电压进行支撑；在PV出力高峰期充电以吸收系统过剩功率，从而对电压稳定控制产生辅助调节效用。

模型决策优化后，性能指标的改善效果如下：

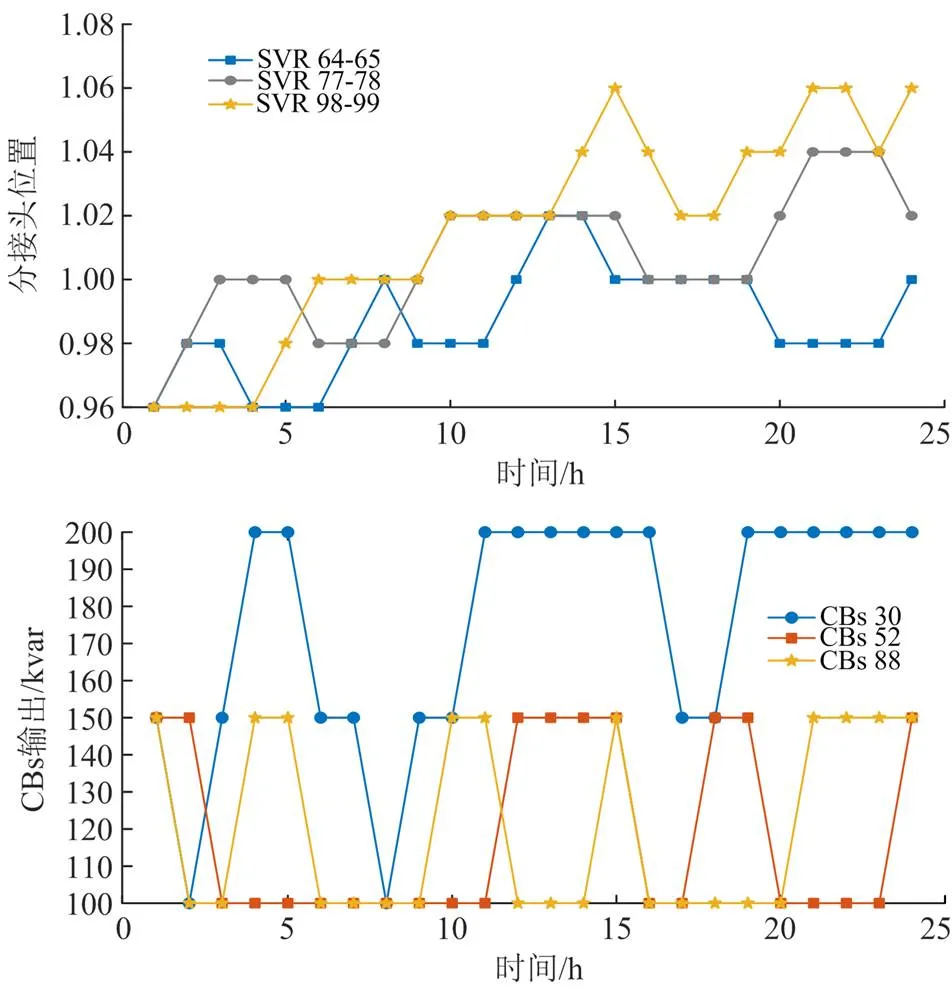
图7 CBs与SVR逐时分布情况

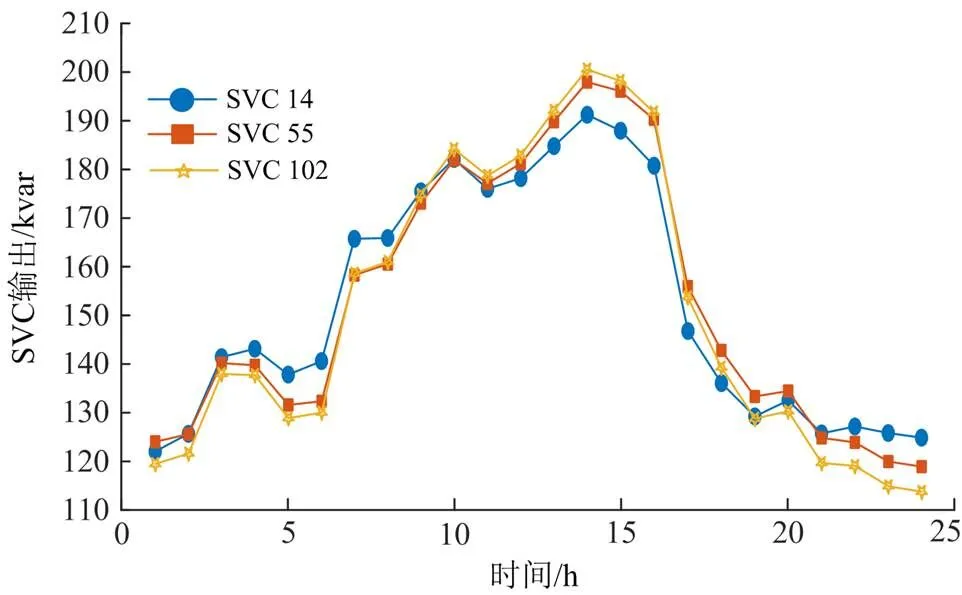
图8 SVC逐时分布情况

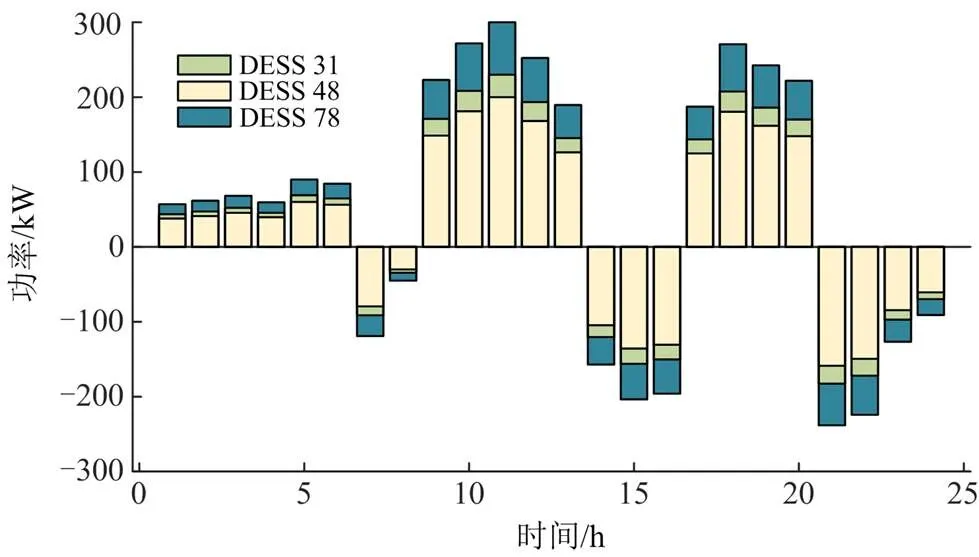
图9 分布式储能时序充/放电功率

1) 可观节点各相电压偏移率

如表6所示，节点各相电压偏移均有不同程度的改善，控制策略对电压越限问题的优化效果显著。

表6 节点各相电压偏移优化效果

Table 6 Optimization effect of node phase voltage offset

2) 线路损耗

如图10所示，11：00—20：00为线损高峰期，初始线损峰值为363.70 kW，日均线损为185.26 kW；优化后损耗峰值降为171.96 kW，日均线损为112.38 kWh，同比下降52.72%与39.34%。可见，策略优化后系统线损情况得到明显改善。

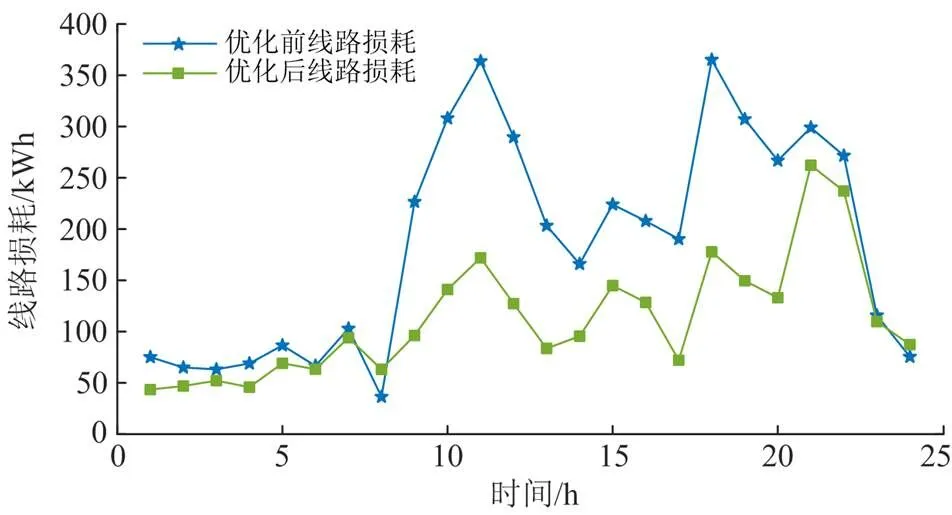
图10 线路损耗优化效果

3) 局部母线电压三相不平衡

针对不平衡节点母线的电压三相不平衡优化效果如图11所示。系统初始不平衡度均超过2%的规定，峰值达到6.4%。而经算法控制后，不平衡度均限制在2%以内，满足运行要求。可知，所提算法可缓解母线电压不平衡问题，减少电压负序电压分量引入的不良影响，提升局部母线电压品质。

图11 局部母线电压三相不平衡度优化效果

5 结论

考虑到非全实时观测配电网无法使用基于全局负荷信息的传统无功优化方法，本文提出了一种含深度学习代理模型的电压无功优化控制进化方法，并通过仿真算例验证，算法应用于非全实时观测的三相不平衡配电网无功优化过程中具备有效性。

1) 在不同感知测试条件下，相较于普通DNN模型，深层HWN具有更高的拟合精度，适用于较大规模配电网的非线性电气参数拟合。

2) 针对性能指标安全阈值，对NSGA-II算法适应性进行改进。据算法最优决策控制后，可实现系统电压越限问题及局部母线三相电压不平衡度的优化调控，降低线路损耗，提升配电网运行品质。

3) HWN-NSGA-II代理辅助进化算法，在实时应用中仅须获取局部负荷信息，无需在线潮流计算，即可实现VVC策略的快速求取，在测量缺失条件下仍具有较强的准确度。

所提HWN-NSGA-II代理辅助进化算法为有源配电网VVC快速决策提供了新工具。下一阶段将测试更多具备潜力的深度网络模型结构，在计算框架中统筹考虑储能使用寿命成本、衰减表征及设备调压成本等因素，并进行算法适用性测试与改进。

[1] 彭生江, 陆军, 张中丹, 等. 光伏接入对电网的影响研究[J]. 电力系统保护与控制, 2021, 49(5): 157-164.

PENG Shengjiang, LU Jun, ZHANG Zhongdan, et al. Research on the influence of photovoltaic access on a power grid[J]. Power System Protection and Control, 2021, 49(5): 157-164.

[2] 刘科研, 贾东梨, 王薇嘉, 等. 考虑分布式光伏电源接入模式的低压配电网不平衡线损计算方法[J]. 电力建设, 2021, 42(10): 129-138.

LIU Keyan, JIA Dongli, WANG Weijia, et al. Calculation method of unbalanced line loss in low-voltage distribution network considering the access mode of distributed photovoltaic generation[J]. Electric Power Construction, 2021, 42(10): 129-138.

[3] LI R, WONG P, WANG K, et al. Power quality enhancement and engineering application with high permeability distributed photovoltaic access to low-voltage distribution networks in Australia[J]. Protection and Control of Modern Power Systems, 2020, 5(3): 183-189.

[4] BOZALAKOV D, VANDOORN T, MEERSMAN B, et al. Damping-based droop control strategy allowing an increased penetration of renewable energy resources in low-voltage grids[J]. IEEE Transactions on Power Delivery, 2016, 31(4): 1447-1455.

[5] 魏剑啸, 粟忠来, 杨波, 等. 配电台区无功功率及三相不平衡电容调节的研究[J]. 电力系统保护与控制, 2019, 47(16): 71-79.

WEI Jianxiao, SU Zhonglai, YANG Bo, et al. Study on reactive power and three-phase unbalance regulated by capacitor in distribution network[J]. Power System Protection and Control, 2019, 47(16): 71-79.

[6] 孙志鹏, 陶顺. 基于电流相位估计的三相不平衡条件下配变损耗计算[J]. 电力工程技术, 2020, 39(3): 114-119.

SUN Zhipeng, TAO Shun. Calculation of distribution loss under three-phase unbalance based on current phase estimation[J]. Electric Power Engineering Technology, 2020, 39(3): 114-119.

[7] 魏梅芳, 胡毕正, 庞文龙, 等. 基于动态三相不平衡度的配电网线损计算方法研究[J]. 智慧电力, 2020, 48(2): 104-108.

WEI Meifang, HU Bizheng, PANG Wenlong, et al. Calculation method of distribution line loss based on dynamic three-phase unbalance degree[J]. Smart Power, 2020, 48(2): 104-108.

[8] 柴园园, 刘一欣, 王成山, 等. 含不完全量测的分布式光伏发电集群电压协调控制[J]. 中国电机工程学报, 2019, 39(8): 2202-2212.

CHAI Yuanyuan, LIU Yixin, WANG Chengshan, et al. Coordinated voltage control for distributed PVs clusters with incomplete measurements[J]. Proceedings of the CSEE, 2019, 39(8): 2202-2212.

[9] 曾顺奇, 吴杰康, 李欣, 等. 考虑拓扑变化的配电网PMU多阶段优化配置[J]. 广东电力, 2021, 34(9): 51-59.

ZENG Shunqi, WU Jiekang, LI Xin, et al. Multi-stage optimal configuration of PMU considering changes in distribution network topology[J]. Guangdong Electric Power, 2021, 34(9): 51-59.

[10] 唐冬来, 郝建维, 刘荣刚, 等. 基于动态规划的配电台区三相负荷不平衡治理方法[J]. 电力系统保护与控制, 2020, 48(21): 58-66.

TANG Donglai, HAO Jianwei, LIU Ronggang, et al. Control method of three phase load imbalance in a distribution station area based on dynamic programming[J]. Power System Protection and Control, 2020, 48(21): 58-66.

[11] SU X, MASOUM M A S, WOLFS P J. Optimal PV inverter reactive power control ADN real power curtailment to improve performance of unbalanced four-wire LV distribution networks[J]. IEEE Transactions on Sustainable Energy, 2014, 5(3): 967-977.

[12] 董雷, 田爱忠, 于汀, 等. 基于混合整数半定规划的含分布式电源配电网无功优化[J]. 电力系统自动化, 2015, 39(21): 66-72.

DONG Lei, TIAN Aizhong, YU Ting, et al. Reactive power optimization for distribution network with distributed generators based on mixed integer semi-definite programming[J]. Automation of Electric Power Systems, 2015, 39(21): 66-72.

[13] 怀全, 候小虎, 何良策, 等. 一种含分布式电源的中低压配电网状态估计方法研究[J]. 电力系统保护与控制, 2018, 46(21): 69-77.

HUAI Quan, HOU Xiaohu, HE Liangce, et al. A method of state estimation for middle voltage and low voltage distribution network with distributed generations[J]. Power System Protection and Control, 2018, 46(21): 69-77.

[14] 李振坤, 陈思宇, 符杨, 等. 基于时序电压灵敏度的有源配电网储能优化配置[J]. 中国电机工程学报, 2017, 37(16): 4630-4640.

LI Zhenkun, CHEN Siyu, FU Yang, et al. Optimal allocation of ESS in distribution network containing DG based on timing-voltage-sensitivity analysis[J]. Proceedings of the CSEE, 2017, 37(16): 4630-4640.

[15] 王澍. 计及状态估计精度的智能配电网PMU多目标最优配置研究[D]. 上海: 上海交通大学, 2019.

WANG Shu. Research on multi-objective optimal placement of PMU in smart distribution network considering the accuracy of state estimation[D]. Shanghai: Shanghai Jiao Tong University, 2019.

[16] LEAL-ROMO F, CHAVEZ-HURTADO J L, RAYAS-SANCHEZ J E. Selecting surrogate-based modeling techniques for power integrity analysis[C] // 2018 IEEE MTT-S Latin America Microwave Conference (LAMC), December 12-14, 2018, Arequipa, Peru.

[17] HENNERON T, PIERQUIN A, CLENET S. Surrogate model based on the POD combined with the RBF interpolation of nonlinear magnetostatic FE model[J]. IEEE Transactions on Magnetics, 2020, 56(1): 1-4.

[18] 崔承刚, 郝慧玲, 杨宁, 等. 基于优化Kriging代理模型的场景分析法求解机组组合问题[J]. 电力系统保护与控制, 2020, 48(22): 49-56.

CUI Chenggang, HAO Huiling, YANG Ning, et al. Scenario analysis based on the optimization Kriging model for solving unit commitment problems[J]. Power System Protection and Control, 2020, 48(22): 49-56.

[19] 段翔兮, 邹琬, 李熠, 等. 基于数据驱动代理模型的城市输电网运行品质调节控制策略[J]. 电力系统保护与控制, 2021, 49(2): 65-73.

DUAN Xiangxi, ZOU Wan, LI Yi, et al. Data driven surrogate model-based operation quality control strategy of an urban transmission network[J]. Power System Protection and Control, 2021, 49(2): 65-73.

[20] 张宇精, 乔颖, 鲁宗相, 等. 含高比例分布式电源接入的低感知度配电网电压控制方法[J]. 电网技术, 2019, 43(5): 1528-1535.

ZHANG Yujing, QIAO Ying, LU Zongxiang, et al. Voltage control for partially visible distribution networks with high DG penetration[J]. Power System Technology, 2019, 43(5): 1528-1535.

[21] 邵美阳, 吴俊勇, 石琛, 等. 基于数据驱动和深度置信网络的配电网无功优化[J]. 电网技术, 2019, 43(6): 1874-1885.

SHAO Meiyang, WU Junyong, SHI Chen, et al. Reactive power optimization of distribution network based on data driven and deep belief network[J]. Power System Technology, 2019, 43(6): 1874-1885.

[22] 廖文龙, 于贇, 王煜森, 等. 基于图卷积网络的配电网无功优化[J]. 电网技术, 2021, 45(6): 2150-2160.

LIAO Wenlong, YU Yun, WANG Yusen, et al. Reactive power optimization of distribution network based on graph convolutional network[J]. Power System Technology, 2021, 45(6): 2150-2160.

[23] 程乐峰, 余涛, 张孝顺, 等. 机器学习在能源与电力系统领域的应用和展望[J]. 电力系统自动化, 2019, 43(1): 15-31.

CHENG Lefeng, YU Tao, ZHANG Xiaoshun, et al. Machine learning for energy and electric power systems: state of the art and prospects[J]. Automation of Electric Power Systems, 2019, 43(1): 15-31.

[24] SRIVASTAVA R K, GREFF K, SCHMIDHUBER J. Highway networks[J]. Computer Science, 2015(7): 12-21.

[25] 王志强, 方正, 刘文霞, 等. 基于概率多场景的柔性配电网鲁棒运行优化[J]. 电力自动化设备, 2019, 39(7): 37-44.

WANG Zhiqiang, FANG Zheng, LIU Wenxia, et al. Robust operation optimization of flexible distribution network based on probabilistic multi-scenario[J]. Electric Power Automation Equipment, 2019, 39(7): 37-44.

[26] 贺强, 晁海亮, 闫明, 等. 考虑风光不确定性的电力系统概率潮流计算[J]. 电网与清洁能源, 2021, 37(6): 113-119, 126.

HE Qiang, CHAO Hailiang, YAN Ming, et al. Probabilistic power flow calculation of the power system considering wind power and photovoltaic uncertainties[J]. Power System and Clean Energy, 2021, 37(6): 113-119, 126.

[27] ZHAO Zhida, YU Hao, LI Peng, et al. Optimal placement of PMUs and communication links for distributed state estimation in distribution networks[J]. Applied Energy, 2019, 256.

[28] PANT M, SNASEL V, VERMA S. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems[J]. IEEE Access, 2021, 9: 57757-57791.

[29] 张健磊, 高湛军, 孙旭日, 等. 基于NSGA-Ⅱ算法的有源配电网故障定位方法研究[J]. 电测与仪表, 2020, 57(9): 33-39.

ZHANG Jianlei, GAO Zhanjun, SUN Xuri, et al. Research on fault location method for active distribution network based on NSGA-Ⅱ algorithm[J]. Electrical Measurement & Instrumentation, 2020, 57(9): 33-39.

[30] 肖怀硕, 李清泉, 施亚林, 等. 灰色理论–变分模态分解和NSGA-II优化的支持向量机在变压器油中气体预测中的应用[J]. 中国电机工程学报, 2017, 37(12): 3643-3653.

XIAO Huaishuo, LI Qingquan, SHI Yalin, et al. Prediction of dissolved gases in oil for transformer based on grey theory-variational mode decomposition and support vector machine improved by NSGA-II[J]. Proceedings of the CSEE, 2017, 37(12): 3643-3653.

[31] AZAZA M, WALLIN F. Multi objective particle swarm optimization of hybrid micro-grid system: a case study in Sweden[J]. Energy, 2017, 123: 108-118.

[32] GE Y, LIN Y, HE Q, et al. Geometric optimization of segmented thermoelectric generators for waste heat recovery systems using genetic algorithm[J]. Energy, 2021, 233.

[33] 谢景海, 苏东禹, 卢诗华, 等. 基于改进蚁群算法的输电线路路径规划关键技术[J]. 电测与仪表, 2020, 57(4): 122-128.

XIE Jinghai, SU Dongyu, LU Shihua, et al. Key technology of transmission line path planning based on improved ant[J]. Electrical Measurement & Instrumentation, 2020, 57(4): 122-128.

An evolutionary algorithm for Volt/Var control in an active distribution network with a deep learning surrogate mode

PAN Sirong, LIU Youbo, TANG Zhiyuan, ZHANG Xi, QI Haonan, LIU Junyong

(College of Electrical Engineering, Sichuan University, Chengdu 610065, China)

The integration of large-scale distributed renewable energy sources brings new challenges to the active distribution network (ADN), including the three-phase imbalance problem, unexpected voltage violations and increased line losses. However, due to the incomplete installation of measurement equipment in the current distribution network, it is difficult to accurately obtain the load data of some nodes. Therefore, the traditional ADN voltage control method based on global observation is difficult to meet the actual control requirements. To solve these problems, a fast Volt/Var control (VVC) evolutionary algorithm with a deep learning surrogate model is proposed. In the development of the algorithm, a highway neural network is first designed as the surrogate model to accurately fit the mapping relationship between limited measured load information, voltage regulation control strategy and system performance indices. Then, the trained surrogate model is embedded into the iterative optimization process of the non-dominated sorting genetic algorithm, and the voltage deviation rate, three-phase unbalance degree and line losses indicators are directly calculated, and the data-driven distribution network VVC strategy can be quickly obtained. A modified IEEE 123-node three-phase distribution network is employed to verify the advantages and efficiency of the proposed algorithm.

active distribution network; three-phase unbalance; Volt/Var control; highway neural networks; non-dominated sequencing genetic algorithm; surrogate-assisted model

10.19783/j.cnki.pspc.211509

国家自然科学基金项目资助(51977133)

This work is supported by the National Natural Science Foundation of China (No. 51977133).

2021-11-07；

2022-02-23

潘思蓉(1997—)，女，硕士研究生，主要研究方向为主动配电网规划与运行；E-mail: pansirong@stu.scu.edu.cn

刘友波(1983—)，男，博士，副教授，博士生导师，主要研究方向为电力系统机器学习算法、主动配电网规划与运行；E-mail: liuyoubo@scu.edu.cn

唐志远(1992—)，男，通信作者，博士，副研究员，主要研究方向为考虑新能源并网的新型电力系统控制及规划运行、分布式控制及优化。E-mail: tangzhiyuan@scu.edu.cn

(编辑 周金梅)