考虑电动汽车时空负荷分布特性的主动配电网动态重构

程 杉，钟仕凌，尚冬冬，魏康林，王 灿

考虑电动汽车时空负荷分布特性的主动配电网动态重构

程 杉1，钟仕凌1，尚冬冬1，魏康林2，王 灿1

(1.电力系统智能运行与安全防御宜昌市重点实验室(三峡大学)，湖北 宜昌 443002；2.智能终端四川省重点实验室(宜宾学院智能制造学院)，四川 宜宾 644000)

实现电动汽车(Electric Vehicle, EV)规模化发展并与电网双赢的关键问题之一是如何提高EV充电负荷的预测准确性，并保证含大规模EV充电负荷的配电网运行的安全性和经济性。考虑EV时空负荷分布特性，建立了主动配电网动态重构与有功、无功联合优化数学模型，并给出了其求解方法。首先，根据出行链技术和马尔可夫决策理论，考虑天、人、路对EV的影响因素，构建了EV单位能耗模型和充电负荷的时空分布预测模型。其次，提出考虑储能系统、有载分接开关、投切电容器组、静止无功补偿装置和动态重构多种主动管理措施，计及经济、技术指标和各设备、系统运行约束，建立了含EV的主动配电网动态重构与有功-无功联合优化数学模型。然后，为了提高所构建模型的求解效率，通过二阶锥松弛和变量乘积线性化方法将非凸等式约束和非线性不等式约束线性化后，将原始的混合整数非线性规划问题转化为易求解计算的混合整数二阶锥问题。最后，基于修改的IEEE33节点系统进行仿真实验和对比分析，结果验证了所提方法的有效性和优越性。

电动汽车；时空分布；主动配电网；二阶锥松弛；动态重构

0 引言

全球尤其中国的EV产业正进入加速发展的新阶段[1-5]。虽然《新能源汽车产业发展规划》明确要求城市各区域多配置充电设施，但是EV具有道路交通网络负荷和电力网络负荷的双重属性，其驾驶行为和充电行为会受到路网和电网的交替影响[6]。因此，实现EV规模化发展并与电网双赢的关键问题之一是如何综合考虑车-路-网的耦合性来提高EV充电负荷预测的准确性[7-8]并保证含大规模EV充电负荷的配电网运行的安全性和经济性[1,9]。

主动配电网(Active Distribution Network, ADN)技术是解决分布式新能源(Distributed Generation, DG)并网运行控制、电网与EV及其充放电设施互动、智能配用电问题的有效解决方案[10]。ADN通过组合控制DG、储能、可控负荷等资源从而提高配电网对可再生能源的接纳能力，提升能源利用效率并实现更高级别的自动化。目前，国内外学者针对含DG和EV的ADN网络重构开展了广泛的研究，但鲜有研究考虑EV负荷的时空分布特性和EV与交通系统、配电网的耦合性。

一方面，EV负荷的时空特性对电网运行的影响主要是由EV出行行为导致充电位置的空间变化性和充电时间的不确定性所引起的。文献[11]计及交通网络拓扑特性，基于蒙特卡罗方法预测了EV充电负荷的时空分布，并分析了负荷时空分布特性对配电网潮流的影响；而文献[12]在综合考虑EV与智能电网和智能交通网络间的交互基础上，提出了大规模EV充电的优化调度策略。然而EV时空转移具有随机性，而且交通与天气状况对EV能耗有着显著影响。为此，文献[7]在实时动态随机模拟EV出行路径的基础上，建立了计及实时交通与温度的EV实时单位里程耗电模型；文献[13]则在EV入网时空模型和里程能耗模型基础上，提出了EV充储电站的分散式优化模型。尽管文献[7, 13-14]计及EV出行路径的随机性和能耗影响的多因素性，但没有考虑EV车主充电的主观意愿性，实际上，EV车主的充电需求具有概率性而且其概率密度函数会随着EV出行起止点而变化[15]。因此，为了实现对EV充电负荷时空分布的有效预测，需要建立计及EV出行路径随机性、路网及天气影响耦合性和车主充电主观性的负荷预测模型。

另一方面，EV负荷的时空分布特性也给电力系统的运行带来了挑战[16]，而动态网络重构(Dynamic Network Reconfiguration, DNR)和主动管理措施是实现ADN优化调度的重要方式，两者结合能有效地改善配电网电压分布和提升配电网经济运行水平[17]。文献[18]构建了ADN的动态最优潮流模型，并在ADN各参与元素关键约束线性化出力的基础上，提出了ADN非线性最优潮流问题的二阶锥规划快速求解方法；文献[19]考虑可再生能源出力的时序性与随机性，提出了含高渗透率可再生能源的ADN日前、日内两阶段柔性软开关与联络开关的协调优化控制方法；而文献[20]则考虑DG、EV和其他负荷的不确定性，建立了计及运行经济性和系统电能质量的ADN重构双层优化数学模型并采用改进和声搜索算法对ADN进行分时段动态网络重构。不同于上述研究[19-20]仅集中于ADN的网络重构，文献[21-22]则综合考虑包括DNR、有载分接开关(On Load Tap Changer, OLTC)、投切电容器(Capacitor Banks, CB)、静止无功补偿装置(Static Var Compensation, SVC)无功调节等主动管理元素，建立了ADN最优潮流二阶锥模型。上述研究表明二阶锥形式的潮流模型可准确、高效地计算电网最优潮流分布。

综上，首先本文计及车、路、网的耦合性，提出了考虑EV时空转移随机性的EV充电负荷预测方法，即基于出行链、蒙特卡罗抽样和马尔可夫决策理论，综合考虑温度、交通状况和EV车主主观意愿，建立EV时空转移模型并应用于工作日、双休日、高温日和拥堵日等不同场景的充电负荷预测；其次，针对含EV的ADN，考虑EV的时空分布，DG和储能(Energy Storage System, ESS)调控，OLTC、SVC和CB调节等主动管理元素，以配电网综合运行成本和电压偏差加权最小为目标函数，构建ADN动态重构与无功、有功联合优化数学模型；然后，为提高数学模型的求解效率，利用二阶锥松弛对非凸的潮流约束进行凸化处理，引入支路虚拟端电压变量对非凸的变量乘积项进行变量分离线性化，从而将联合优化数学模型转化为一个混合整数二阶锥规划(Mixed Integer Second-Order Cone Programming, MISOCP)问题；最后，基于修改的IEEE33节点系统算例进行一系列仿真，验证了所建模型和求解方法有效性和优越性。

1 EV时空分布及其能耗模型

虽然EV发展迅速，但市场占有率还较低，难以通过样本数据分析其时空分布特性。本文通过概率密度函数模拟EV出行模型，并结合路网拓扑结构、EV车主充电意愿和马尔可夫决策理论计算EV并网负荷的时空分布。

1.1 EV出行链及其数学表达

如图1所示，根据人们日常活动将出行需求分为回家(Home, H)、工作(Work, W)、上学(School, S)、购物聚餐(Shopping & Eating, SE)、休闲娱乐(Recreation & Entertainment, RE)和其他(Other Things, OT) 6种，包括单目的出行链H-W、H-S/SE/RE/OT和多目的出行链H-W-S/SE/RE/OT。假设出行链途经的地点都可以对EV进行充电。

式中，和随着出行链变化。

1.2 EV出行路径随机性及其模拟

基于马尔可夫决策理论的EV出行路径如图2所示，过程由{,,,,} 5种参数构成。

图2 交通网络示意图

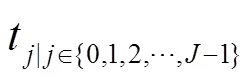
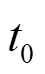
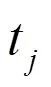
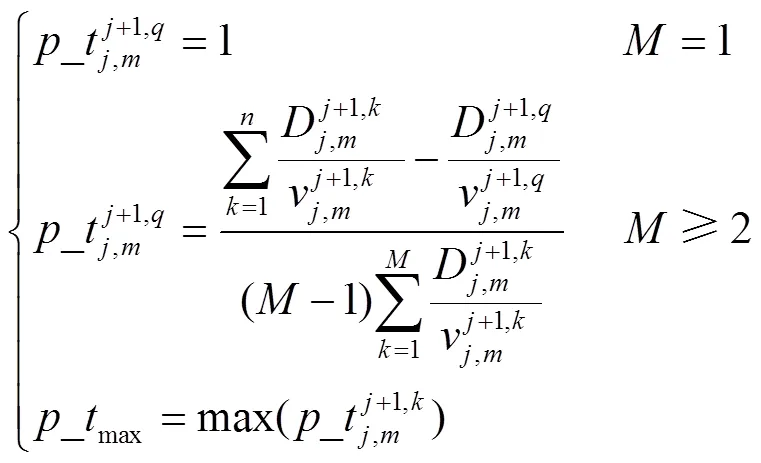
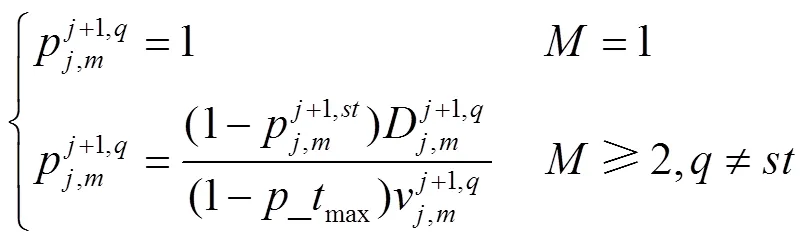
通过式(3)、式(4)可以保证在车主选择路径时，行驶时间越长，被选中的概率越小。

5)表示出行链中的回报值，用于评估EV在某一决策时刻处于某一状态做出行动的优劣。本文中是指EV随机路径模拟的行驶时间，即行驶时间越短，报酬越大。

1.3 EV的单位里程能耗模型和充电模型

1.3.1单位里程能耗模型

计及空调开启的EV每公里耗电量计算如式(6)。

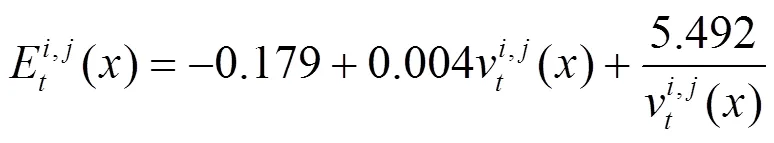
实际温度的变化能影响EV用户空调开启率[13]，具体可表示为

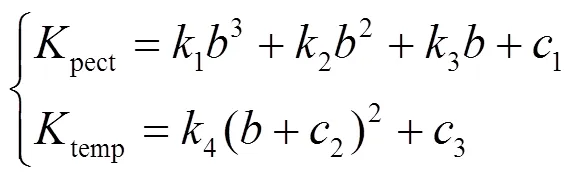
综合式(6)和式(7)，EV的实际每公里耗电量可表示为

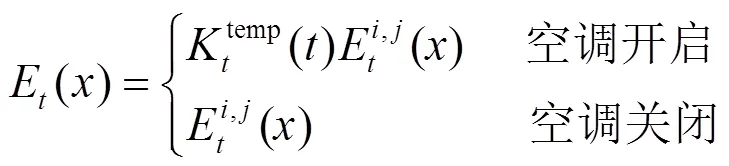
因此，EV在地点的荷电状态计算式为

1.3.2考虑车主主观意愿的EV充电模型

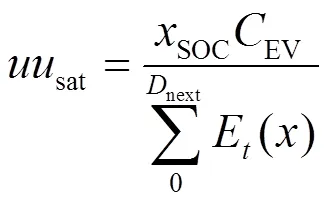
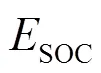
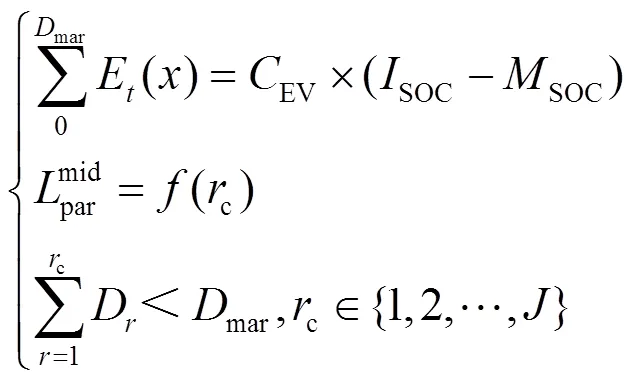
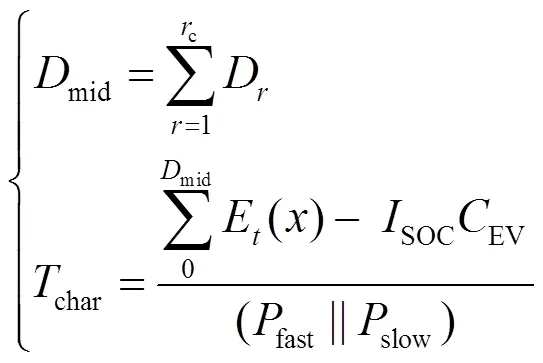
1.4 EV充电负荷

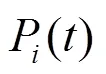
综上，EV充电负荷计算流程图如图3所示。

图3 EV时空充电负荷计算流程图

2 考虑动态重构的配电网优化运行模型

EV的时空不确定性使其负荷具有随机性，易引起配电网过负荷，增加系统损耗，造成电压畸形甚至失稳。本文计及综合运行成本与电压偏差等指标、主动管理技术和各设备与系统运行约束，建立ADN动态重构与无功、有功联合优化数学模型。

2.1 目标函数

目标函数由综合运行成本和电压偏差指标加权组成，如式(18)。

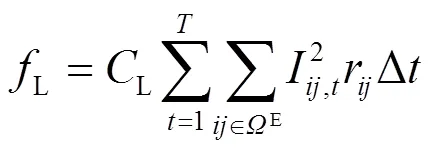
2.2 约束条件

1) 功率平衡约束

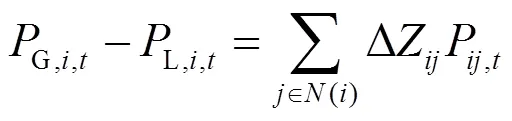
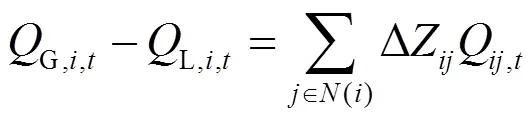
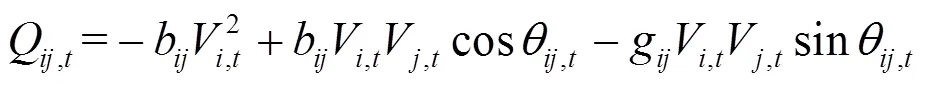
2) 支路载流量约束

3) 节点电压约束

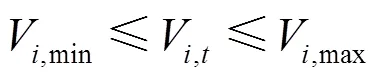
4) 辐射型网络约束

配电网络一般都是闭环设计、开环运行，利用最小生成树算法确保重构过程中配电网络的辐射结构，即满足式(29)，其中，涉及到求解配电网对偶图的方法如附录A所示。

5) OLTC运行约束[18]

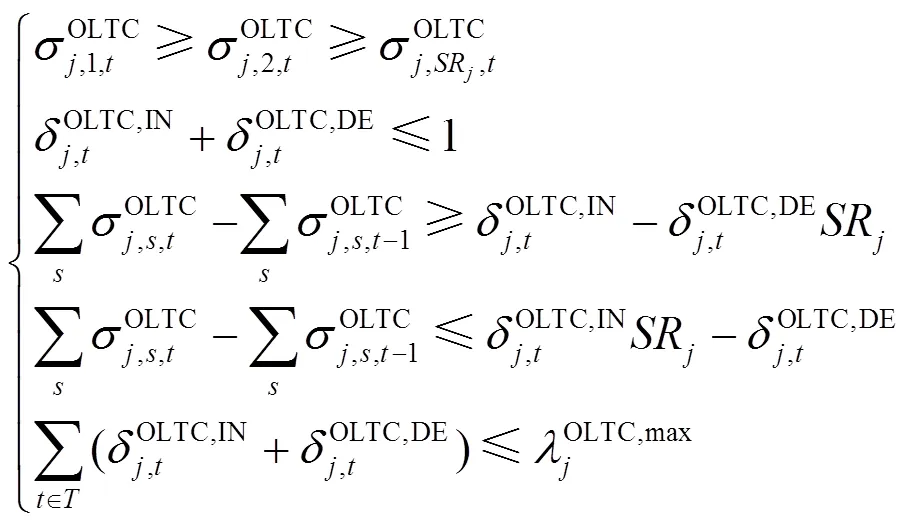
6) CB约束

CB为离散型无功补偿，其约束为

7) SVC约束

SVC为连续无功调节装置，其约束为

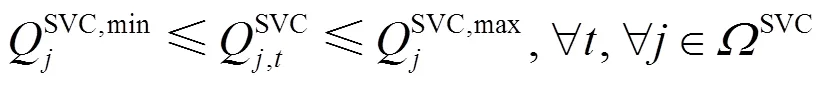
8) DG出力约束

DG接入的有功功率和无功功率约束为

9) ESS约束

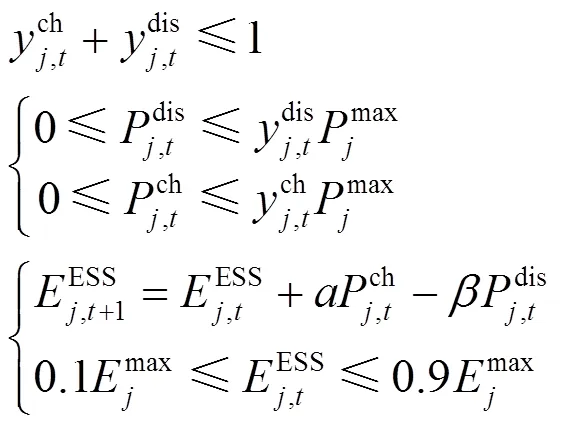
10) 开关动作次数约束

频繁的开关变化会给配电网的安全稳定运行和保障电能质量带来挑战，考虑开关使用寿命、开关动作成本且防止对系统造成较大冲击，本文综合考虑一天内风光出力和负荷变化情况，以一天为周期产生日重构决策。

2.3 模型转化

上述联合优化模型为混合整数非线性规划(Mixed-Integer Nonlinear Programming, MINLP)问题，难以求解，采用如下方法对模型进行转化。

1) 潮流方程的二阶锥松弛

潮流方程为非凸形式，二阶锥松弛可保证将其松弛后解的最优性和近似精度[25]。首先对潮流方程进行变量替换，定义：

进行变量代换，则潮流方程转化为

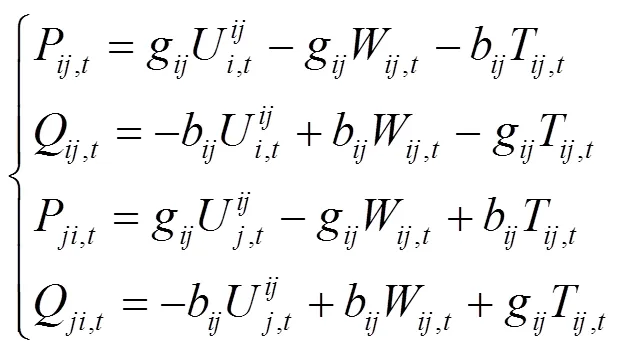
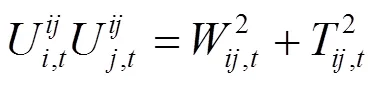
对式(40)进行二阶锥松弛后约束为

2) 非线性约束的线性化

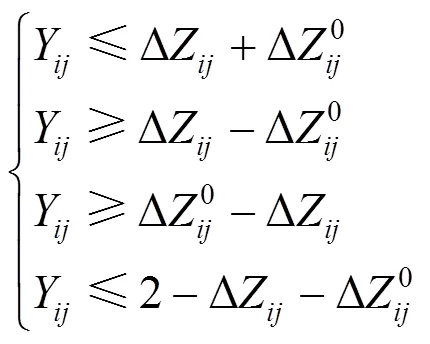
通过转化，可见：除式(41)为二阶锥约束，其余均为线性形式，将原MINLP问题转化为MISOCP问题，求解效率大幅提高。

3 算例分析

硬件环境为Intel(R) Core(TM) i3-7100 CPU @ 3.90 GHz，8 GB内存。如图4所示，以修改的IEEE 33节点系统与某城区路网耦合网络为算例(交通节点(Traffic Network Node, TNN)与配电网节点(Distribution Network Node, DNN)的耦合关系、各时段网络道路饱和度设置[24]、各道路具体距离见附录C)，基于MATLAB R2016a编程，利用YALMIP工具包及CPLEX算法包求解转化后的MISOCP问题。

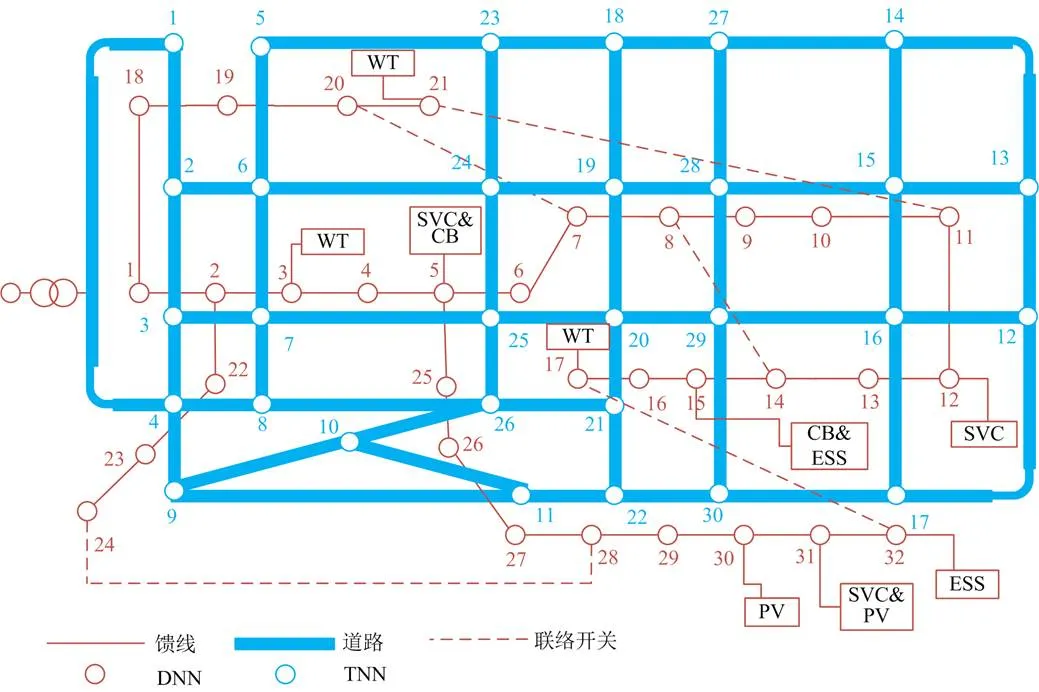
图4 路-网耦合拓扑示意图

2) 主动管理设备参数：ESS、PV、WT、SVC、CB、OLTC和24 h动态负荷数据的具体参数见附录D，总的基础负荷为67.12 MWh和41.55 Mvarh。

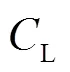
3.1 EV的充电负荷时空分布

温度能耗模型和用户主观充电意愿模型使充电时空分布更加真实，基于上述考虑，本文根据输入参数的不同，对工作日、双休日、高温日和拥堵日4个不同的场景进行建模分析。

3.1.1工作日与双休日充电负荷分布

该区域各节点在工作日、双休日的充电负荷分布如图5所示。在工作日，工业区用电高峰时段主要集中在09：00 —12：00，居民区和商业区用电高峰时段主要集中在18：00—22：00，其余时间各地点充电负荷几乎为0。而双休日不上班，工业区充电负荷基本为0，居民区和商业区的充电负荷在09：00—24：00呈均匀分布。这种时空分布主要是由于行程的出行链结构和出发时间决定的。工作日和双休日中各区域的负荷峰值时段相较出发起始时段均延迟1～3 h，这个时间差为交通状况导致。此外，工作日的负荷峰值大概为双休日负荷峰值的1.5倍，这是因为双休日中30%的出行车辆数量为闲置，从而未产生额外充电负荷。

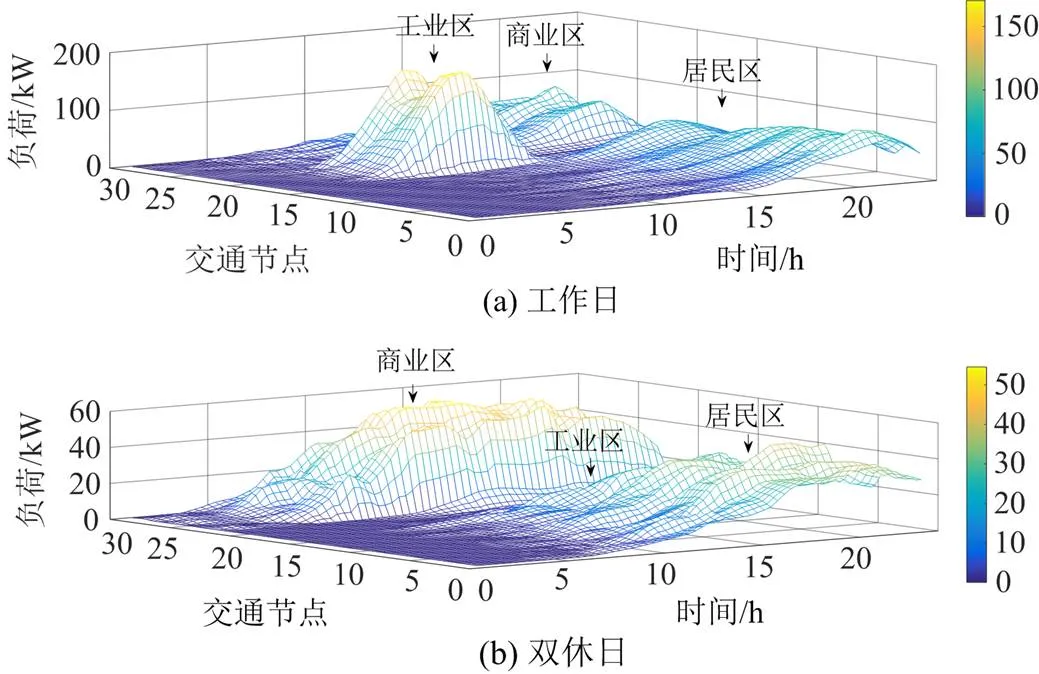
图5 工作日和双休日的充电负荷时空分布

3.1.2高温日与拥堵日充电负荷分布

为了研究温度和交通状况对充电需求的影响，进行了高温日和拥堵日的充电负荷预测，结果如图6所示。需要说明的是，高温日和拥堵日的输入参数除温度和EV行驶速度外，其余与工作日相同。可以看出，高温日的时空分布与工作日基本一致，但前者负荷峰值急剧增加，增长负荷占工作日负荷的80.1%。这是由于在高温日EV的电能消耗不仅用于交通，还有一部分用于空调制冷。而对于拥堵日，充电负荷幅值相较工作日负荷增长52.3%，且负荷整体出现了时间维度上的迟滞，尤其是居民区在20：00以后才逐渐进入负荷高峰，这是因为EV的拥堵导致交通耗时增加，从而造成了接入时段整体后移。

3.2 优化结果分析

分析了不同场景下的充电负荷后，可发现充电负荷在时间和空间上都有较大波动。为满足EV时空负荷接入后ADN的安全、稳定运行，本文选取负荷波动最大的拥堵日进行对比分析。

图6 高温日和拥堵日的充电负荷时空分布

模式1：仅考虑ESS和DG有功功率优化。

模式2：在模式1的基础上考虑电压偏差。

模式3：在模式2的基础上添加OLTC、CB、SVC进行有功-无功功率联合优化。

模式4：在模式3有功、无功功率联合优化的基础上添加动态网络重构。

由于充电负荷波动很大，当不考虑ESS和DG时，电压会低于0.95 p.u.，电压越下限，所以没有设置对比分析。在考虑有功优化的基础上，4种模式下的优化结果如表1所示，对比模式1和模式2可以看出，运行成本略微增加，但电压的越下限风险明显降低(结合图7分析)；对比模式2和模式3可以看出，有功-无功联合优化显著降低线损成本和主动购电费用，分别降低了49.4%和8.9%，同时大幅度减少DG的弃风、弃光现象，降低了81.1%；对比模式3和模式4可以看出，考虑动态网络重构可以进一步降低网损和主动购电费用，分别降低了33.8%和4.4%，同时促进了DG的完全消纳，表明在EV时空负荷接入后动态重构和有功-无功联合优化对提高配电网经济运行方面有良好的效果。

表1 4种模式下的优化结果

4种模式下的网络节点电压分布如图7所示。从图中可发现，模式1和模式2由于接入的负荷较大，并且未考虑OLTC、CB、SVC，导致配电网无功电压补偿不足，电压水平普遍偏低，但模式2考虑了电压偏差，电压在0.95 p.u.附近的波动(图中的蓝色部分)明显减少；模式3采用了有功无功联合优化后，显著提高了各节点的电压水平，但电压曲线变化较大，这是由于充电负荷随时间变化较大导致的；而动态重构可以改善电压波动[20]，对比模式2和模式3，模式4的动态重构和有功-无功联合优化使节点电压更为平稳，全部在0.97～1.03 p.u.之间，可看出通过改变网络拓扑结构能有效平抑时空负荷引起的电压波动，提高配电网电压质量，也说明当EV时空负荷接入后，动态重构和多种主动管理措施能保证配电网的安全、经济运行。另外，添加电压偏移阈值后，运行成本只是略微上升，运营商可以通过牺牲一定的经济性，改变电压偏移的权重，从而降低电压越限的风险。

无功补偿的出力如图8(a)所示，节点5的CB和SVC设备在06：00后出力逐渐升高，并在10：00达到峰值，这是由于节点5相连的节点25对应的区域为工业区，其用电高峰主要集中在09：00—12：00，同时此时段系统的总负荷也最大，所以节点5的补偿值在该时段达到最大，并且其他节点的补偿值也有所提高。储能的充放电是由电价和负荷共同决定的，如图8(b)所示，00：00—07：00和09：00—12：00电价分别处于最低和最高，储能受分时电价的影响在00：00—07：00进行充电，在09：00—12：00进行放电。节点15和节点32所属的居民区和商业区在20：00以后才进入负荷高峰，为减轻高负荷对电网的冲击，储能在13：00—19：00进行充电，在20：00—24：00进行放电，可以看出储能在EV接入后起到了良好的削峰填谷的作用。另外，两个节点储能的充、放电趋势大致相同，说明电价是影响储能出力的主要原因。

3.3 有效性分析

3.3.1松弛误差分析

3.3.2计算速度分析

为验证模型的优越性，现将模型转化前后的求解速度进行对比。转换前优化模型为MINLP，对于大规模非线性规划问题，现有的求解方法有智能算法和传统的数值方法，本文将以粒子群算法和Knitro算法包为例进行比较，如表2所示。可以看出，直接求解所耗时间长且难以求解，将模型转化为MISOCP后，求解效率显著提升。

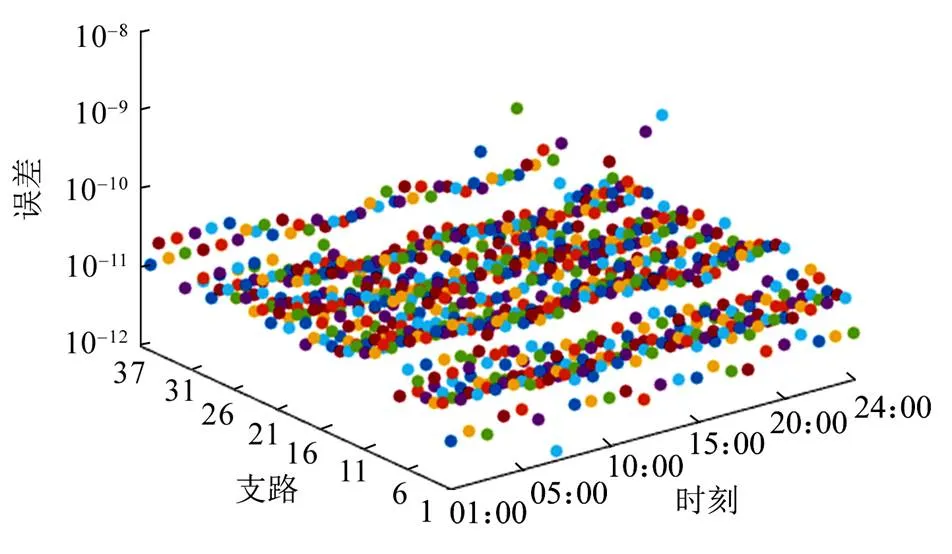
图9 二阶锥松弛误差

表2 不同方法求解速度比较

4 结论

本文提出了一种考虑EV时空分布特性的ADN动态重构，根据仿真结果得到以下结论：

1) 计及温度、交通状况和车主主观意愿的EV充电负荷时空分布预测模型考虑了天、人、路对EV出行路径的影响，可以真实地反映EV出行路径的随机性和各因素间的耦合性。

2) 计及主动管理技术和考虑经济性与技术性指标的ADN动态重构与有功-无功联合优化模型可显著降低网损、促进DG消纳和减少系统电压波动；同时可以通过改变经济性与技术性指标权重得到体现偏好的ADN运行方案。

3) 二阶锥松弛和变量乘积线性化有效地将联合优化模型进行凸化处理，在满足工程求解精度的同时降低了求解的复杂度，显著提高了模型的求解效率。

4) 储能削峰填谷作用明显，EV充电站合理配置储能系统将进一步降低EV时空负荷随机性对电网的冲击，提高ADN运行的经济性和可靠性。

附录A

现有配电网重构相关文献往往不涉及对偶图，根据图论提出一种求解配电网对偶图的算法。

任意一个平面上的图G，若满足以下条件：

求解对偶图的具体步骤如下所述。

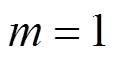
步骤2：判断有无与节点相连的两个相异节点、。若不存在，则与节点相连节点组成的支路在对偶图无对应支路。

步骤3：使用floyd算法求解节点和之间所有节点编号都不大于的最短路径。将该路径和路径、共同组成第个最小环并储存。

步骤5：搜索并记录原图G中个最小环中每个支路对应对偶节点之间的连接状态。

附录B

附表B1 工作日和双休日出行链结构和构成比例

Attached Table B1 Trip chain composition and proportion on weekdays and weekends

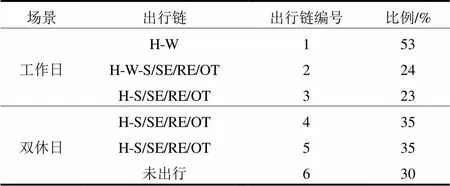
场景出行链出行链编号比例/% 工作日H-W153 H-W-S/SE/RE/OT224 H-S/SE/RE/OT323 双休日H-S/SE/RE/OT435 H-S/SE/RE/OT535 未出行630

附表B2 不同出行链的概率分布

Attached Table B2 Probability distribution of different trip chains

场景出行链编号上午下午 工作日1N(6.92,1.24)N(17.47,1.80) 2N(6.92,1.24)N(17.47,1.80) 3N(6.92,1.24)— 双休日4N(6.92,1.24)— 5—N(17.47,1.80) 6——

附录C

附表C1 路-网节点耦合信息

Attached Table C1 Coupling between TNN and DNN

交通节点配电网节点交通节点配电网节点交通节点配电网节点 111212234 221313249 3314142511 4615152625 52416162726 61917292810 7201828298 821195307 922202331— 1030211832— 1117222733—

附表C2 交通道路饱和度

Attached Table C2 Road saturation within a day

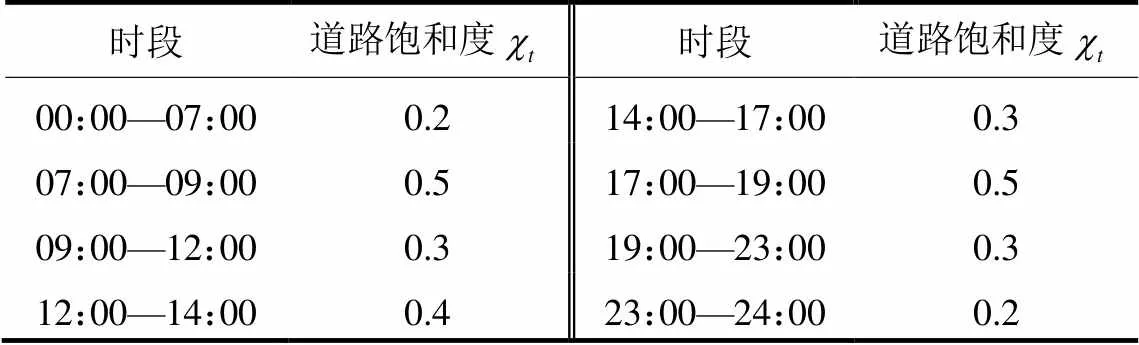
时段道路饱和度时段道路饱和度 00：00—07：000.214：00—17：000.3 07：00—09：000.517：00—19：000.5 09：00—12：000.319：00—23：000.3 12：00—14：000.423：00—24：000.2

附表C3 交通道路长度

Attached Table C3 Road length

道路长度/km道路长度/km道路长度/km (1,2)10.2(9,11)10.1(18,27)9.7 (1,4)10.4(10,11)9.0(19,20)10.0 (2,3)10.3(10,21)10.1(19,24)10.4 (2,5)10.5(11,22)10.2(19,28)8.8 (2,6)10.6(12,13)10.3(20,21)9.1 (3,4)10.4(12,16)10.6(20,25)10.5 (3,7)10.7(12,17)10.7(20,29)8.9 (4,8)10.8(13,14)10.4(21,22)10.2 (4,9)9.9(13,15)10.5(21,25)10.5 (5,6)10.6(14,15)9.5(22,30)11.0 (5,23)10.3(14,28)9.7(23,24)10.4 (6,7)9.7(15,16)8.6(24,25)9.5 (6,24)9.4(15,28)8.8(25,26)9.6 (7,8)10.8(16,17)10.7(27,28)9.8 (7,25)9.5(16,29)8.9(28,29)8.9 (8,10)10.0(17,30)11.0(29,30)11.0 (8,26)9.6(18,19)8.9—— (9,10)9.9(18,23)10.3——

附录D

附表D1 WT参数

Attached Table D1 Parameters of WT

接入节点输出有功上限/kW功角上限功角下限 3,17,215000.9-0.9

附表D2 PV参数

Attached Table D2 Parameters of PV

接入节点输出有功上限/kW功角上限功角下限 16,19,30,314000.9-0.9

附表D3 ESS参数

Attached Table D3 Parameters of ESS

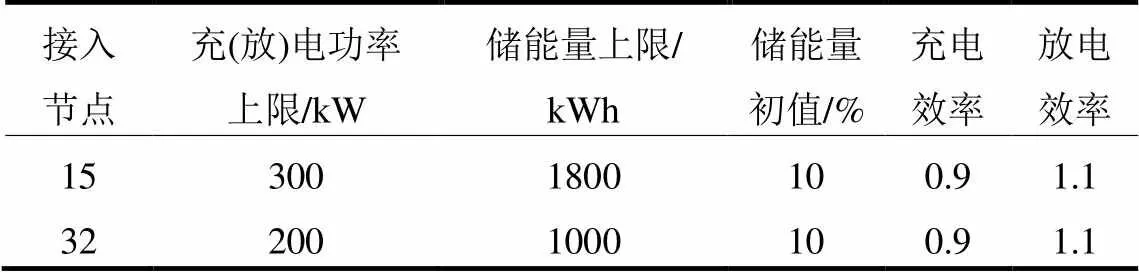
接入节点充(放)电功率上限/kW储能量上限/kWh储能量初值/%充电效率放电效率 153001800100.91.1 322001000100.91.1

附表D4 CB参数

Attached Table D4 Parameters of CB

接入节点单位容量/kvar最大组量 5,15505

附表D5 SVC参数

Attached Table D5 Parameters of SVC

接入节点最小无功输出/kvar最小无功输出/kvar 5,12,31-100300

附图D1 动态负荷

Attached Fig. D1 Dynamic load

附图D2 分时电价

Attached Fig. D2 Time-sharing price

[1] 程杉, 陈梓铭, 徐康仪, 等. 基于合作博弈与动态分时电价的电动汽车有序充放电方法[J]. 电力系统保护与控制, 2020, 48(21): 15-21.

CHENG Shan, CHEN Ziming, XU Kangyi, et al. An orderly charging and discharging method for electric vehicles based on a cooperative game and dynamic time-of-use price[J]. Power System Protection and Control, 2020, 48(21): 15-21.

[2] 程杉, 杨堃, 赵孟雨, 等. 计及电价优化和放电节制的电动汽车充电站优化调度[J]. 电力系统保护与控制, 2021, 49(11): 1-8.

CHENG Shan, YANG Kun, ZHAO Mengyu, et al. Orderly charging and discharging scheduling of an electric vehicle charging station considering price optimization and discharge behavior control[J]. Power System Protection and Control, 2021, 49(11): 1-8.

[3] 刘坚, 熊英, 金亨美, 等. 电动汽车参与电力需求响应的成本效益分析——以上海市为例[J]. 全球能源互联网, 2021, 4(1): 86-94.

LIU Jian, XIONG Ying, KIM H M, et al. Economic assessment of demand response delivered by electric vehicles in Shanghai[J]. Journal of Global Energy Interconnection, 2021, 4(1): 86-94.

[4] 陈浩, 胡俊杰, 袁海峰, 等. 计及配电网拥塞的集群电动汽车参与二次调频方法研究[J]. 中国电力, 2021, 54(12): 162-169.

CHEN Hao, HU Junjie, YUAN Haifeng, et al. Research on supplementary frequency regulation with aggregated electric vehicles considering distribution network congestion[J]. Electric Power, 2021, 54(12): 162-169.

[5] 张怡, 郝思鹏. 不同场景下快速充电站的分层储能配置[J]. 供用电, 2020, 37(7): 94-100.

ZHANG Yi, HAO Sipeng. Hierarchical energy storage configuration of fast charging station in different scenarios[J]. Distribution & Utilization, 2020, 37(7): 94-100.

[6] 杨昕然, 吕林, 向月, 等. “车-路-网” 耦合下电动汽车恶劣充电场景及其对城市配电网电压稳定性影响[J]. 电力自动化设备, 2019, 39(10): 108-114, 128.

YANG Xinran, LÜ Lin, XIANG Yue, et al. Electric vehicle bad charging scenario and its influence on voltage stability of urban distribution network under "vehicle- road-network" coupling[J]. Electric Power Automation Equipment, 2019, 39(10): 108-114, 128.

[7] 张谦, 王众, 谭维玉, 等. 基于MDP随机路径模拟的电动汽车充电负荷时空分布预测[J]. 电力系统自动化, 2018, 42(20): 59-66.

ZHANG Qian, WANG Zhong, TAN Weiyu, et al. Prediction of temporal and spatial distribution of electric vehicle charging load based on MDP random path simulation[J]. Automation of Electric Power Systems, 2018, 42(20): 59-66.

[8] CHENG S, WEI Z, SHANG D, et al. Charging load prediction and distribution network reliability evaluation considering electric vehicles’ spatial-temporal transfer randomness[J]. IEEE Access, 2020, 8: 124084-124096.

[9] 程杉, 倪凯旋, 赵孟雨. 基于Stackelberg博弈的一体化电站微电网双层协调优化调度[J]. 电力自动化设备, 2020, 40(6): 49-55, 69.

CHENG Shan, NI Kaixuan, ZHAO Mengyu. Stackelberg game based bi-level coordinated optimal scheduling of microgrid accessed with charging-swapping-storage integrated station[J]. Electric Power Automation Equipment, 2020, 40(6): 49-55, 69.

[10] 尤毅, 刘东, 于文鹏, 等. 主动配电网技术及其进展[J]. 电力系统自动化, 2012, 36(18): 10-16.

YOU Yi, LIU Dong, YU Wenpeng, et al. Active distribution network technology and its progress[J]. Automation of Electric Power Systems, 2012, 36(18): 10-16.

[11] 邵尹池, 穆云飞, 余晓丹, 等. “车–路–网”模式下电动汽车充电负荷时空预测及其对配电网潮流的影响[J]. 中国电机工程学报, 2017, 37(18): 5207-5219, 5519.

SHAO Yinchi, MU Yufei, YU Xiaodan, et al. Spatio-temporal prediction of EV charging load and its impact on power flow of distribution network under "vehicle-road-network" mode[J]. Proceedings of the CSEE, 2017, 37(18): 5207-5219, 5519.

[12] LUO Y, ZHU T, WAN S, et al. Optimal charging scheduling for large-scale EV (electric vehicle) deployment based on the interaction of the smart-grid and intelligent-transport systems[J]. Energy, 2016, 97: 359-368.

[13] 程杉, 魏昭彬, 赵子凯, 等. 考虑电动汽车时空接入随机性的充储电站有序充放电分散式优化[J]. 电力自动化设备, 2021, 41(6): 28-35.

CHENG Shan, WEI Zhaobin, ZHAO Zikai, et al. Decentralized optimization of orderly charging and discharging of electric vehicle charging and storage power station considering stochastic space-time access[J]. Electric Power Automation Equipment, 2021, 41(6): 28-35.

[14] FERRO G, MINCIARDI R, ROBBA M. A user equilibrium model for electric vehicles: joint traffic andenergy demand assignment[J]. Energy, 2020, 198.

[15] 刘洪, 张旭, 刘畅, 等. 考虑充电设施充裕性的电动私家车出行与充电需求时序交互分析[J]. 中国电机工程学报, 2018, 38(18): 5469-5478.

LIU Hong, ZHANG Xu, LIU Chang, et al. Interaction analysis of electric private car travel and charging demand considering charging facility abundance[J]. Proceedings of the CSEE, 2018, 38(18): 5469-5478.

[16] XIANG Y, HU S, LIU Y, et al. Electric vehicles in smart grid: a survey on charging load modelling[J]. IET Smart Grid, 2019, 2(1): 25-33.

[17] 倪识远, 张林垚. 考虑动态重构的主动配电网多目标双层优化调度方法[J]. 电力系统保护与控制, 2020, 48(20): 38-47.

NI Shiyuan, ZHANG Linyao. Multi-objective double-layer optimal scheduling method for active distribution network considering dynamic reconfiguration[J]. Power System Protection and Control, 2020, 48(20): 38-47.

[18] 高红均, 刘俊勇, 沈晓东, 等. 主动配电网最优潮流研究及其应用实例[J]. 中国电机工程学报, 2017, 37(6): 1634-1645.

GAO Hongjun, LIU Junyong, SHEN Xiaodong, et al. Research and application of optimal power flow in active distribution network[J]. Proceedings of the CSEE, 2017, 37(6): 1634-1645.

[19] 丛鹏伟, 唐巍, 娄铖伟. 含高渗透率可再生能源的主动配电网两阶段柔性软开关与联络开关协调优化控制[J]. 电工技术学报, 2019, 34(6): 1263-1272.

CONG Pengwei, TANG Wei, LOU Chengwei. Coordination and optimization control of two-stage flexible soft switch and contact switch in active distribution network with high permeability renewable energy[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1263-1272.

[20] 谢琳宇, 唐忠, 黄星宇, 等. 考虑分布式电源和电动汽车不确定性的双层动态配网重构[J]. 电力系统保护与控制, 2020, 48(10): 1-11.

XIE Linyu, TANG Zhong, HUANG Xingyu, et al. Reconfiguration of two-layer dynamic distribution network considering uncertainty of distributed power supply and electric vehicle[J]. Power System Protection and Control, 2020, 48(10): 1-11.

[21] 赵平, 赵期期, 艾小猛. 考虑极限场景的主动配电网重构与无功电压调整联合鲁棒优化[J]. 电工技术学报, 2021, 36(增刊2): 496-506.

ZHAO Ping, ZHAO Qiqi, AI Xiaomeng. Joint robust optimization of active distribution network reconfiguration and reactive voltage adjustment considering limit scenario[J]. Transactions of ChinaElectrotechnical Society, 2021, 36(S2): 496-506.

[22] 王日安, 胡志坚. 主动配电网二阶段鲁棒日前调度优化模型及其求解方法[J]. 武汉大学学报(工学版), 2022, 55(6): 596-608.

WANG Ri’an, HU Zhijian. Two-stage robust day-ahead scheduling optimization model and its solution method for active distribution network[J]. Engineering Journal of Wuhan University, 2022, 55(6): 596-608.

[23] LIU C, WANG J, CAI W, et al. An energy-efficient dynamic route optimization algorithm for connected and automated vehicles using velocity-space-time networks[J]. IEEE Access, 2019, 7: 108866-108877.

[24] XIANG Y, JIANG Z, GU C, et al. Electric vehicle charging in smart grid: a spatial-temporal simulation method[J]. Energy, 2019, 189.

[25] 徐俊俊, 吴在军, 周力, 等. 考虑分布式电源不确定性的配电网鲁棒动态重构[J]. 中国电机工程学报, 2018, 38(16): 4715-4725.

XU Junjun, WU Zaijun, ZHOU Li, et al. Robust dynamic reconfiguration of distribution network considering distributed power uncertainty[J]. Proceedings of the CSEE, 2018, 38(16): 4715-4725.

[26] 徐崇博, 杨晓东, 张有兵, 等. 考虑风险管控的含智能软开关主动配电网随机运行优化方法[J]. 电力系统自动化, 2021, 45(11): 68-76.

XU Chongbo, YANG Xiaodong, ZHANG Youbing, et al. Stochastic operation optimization method of active distribution network with intelligent soft switch considering risk control[J]. Automation of Electric Power Systems, 2021, 45(11): 68-76.

Dynamic reconfiguration of an active distribution network considering temporal and spatial load distribution characteristics of electric vehicles

CHENG Shan1, ZHONG Shiling1, SHANG Dongdong1, WEIKanglin2, WANG Can1

(1. Yichang Key Laboratory of Intelligent Operation and Security Defense of Power System (China Three Gorges University), Yichang 443002, China; 2. China Intelligent Terminal Key Laboratory of Sichuan Province (Yibin University), Yibin 644000, China)

To improve the accurate prediction of electric vehicle (EV) charging load and ensure the stability and economy of the distribution network penetrated with a large scale of EV is one of the key issues in realizing a win-win situation for the EV and distribution network. In this paper, a combined optimization model of active and reactive power for active distribution network reconstruction and its solution method are established considering the characteristics of EV temporal and spatial load distribution. First, from travel chain technology and Markov decision theory, and considering the influence of weather, the EV owner and traffic, an EV unit energy consumption model and the spatial-temporal load model of charging load are constructed. Secondly, considering all of the energy storage system, on-load tap changer, capacitor banks, static var compensation, dynamic reconfigurationof various active management measures, economic indicators and operation constraints, a dynamic reconfiguration and active reactive-power optimization model of an EV active distribution network are established. Then, to improve solution efficiency, the original model is transformed into a mixed integer second order cone model using second-order cone relaxation and variable product linearization methods. Finally, an improved IEEE33 system is used for simulation analysis to verify the effectiveness and superiority of the proposed method.

electric vehicle; spatial-temporal distribution; active distribution network; second-order cone relaxation; dynamic restructuring

10.19783/j.cnki.pspc.211439

国家自然科学基金项目资助(52107108)；电力系统智能运行与安全防御宜昌市重点实验研究项目资助(2020DLXY01)；智能终端四川省重点实验室开放基金项目资助(SCITLAB-1009)

This work is supported by the National Natural Science Foundation of China (No. 52107108).

2021-10-26；

2022-01-17

程 杉(1981—)，男，通信作者，博士，教授，博士生导师，主要从事电力系统运行优化与控制、智能电网能量管理与优化、智能计算及其应用等方向的研究工作；E-mail: hpucquyzu@ctgu.edu.cn

钟仕凌(1997—)，男，硕士研究生，研究方向为电力系统运行优化与控制。E-mail: 849531238@qq.com

(编辑 魏小丽)