城市地下大空间施工重大风险多因素耦合演变模型

雷升祥， 雷 可， 王秀英， 谭忠盛， 黄明利， 田圆圆

(1. 中国铁建股份有限公司， 北京 100855； 2. 北京交通大学 城市地下工程教育部重点实验室，北京 100044； 3. 中铁第五勘察设计院集团有限公司， 北京 102600)

0 引言

为解决日益紧迫的城市环境承载力问题，新建城市地下空间正由点—线—面向区块化、网络化发展，呈现出“上下一体、功能综合、体量庞大、互联互通、空间多维、地下超深”的新趋势[1]。这些新型地下工程已在使用功能、空间规模、结构形态等方面突破了传统地下空间的限制，难以被简单地归为任何一类传统地下空间。为进一步推进城市地下空间的有序发展，引导相关理论技术的针对性研发和产业升级，亟需对这类地下空间作出新的定义。“城市地下大空间”的概念便是在这一背景下提出的。

城市地下大空间由于工程规模大，地质和周边环境复杂，施工难度大大增加，对施工风险的管控提出了更高的要求。由于施工过程的复杂性，城市地下大空间施工风险也呈现出一些有别于一般地下空间的新特性。Perrow[2]的常态事故理论认为，对于一项高复杂度的行动，其相关因素间的动态交互和耦合程度是判定对风险产生影响的重要指标。Leveson[3]认为，事故是一个系统内多种要素在不断反馈和调整的过程中，由于缺少必要的约束而使系统行为突破安全边界的一种涌现现象。诸多实际案例和理论研究表明： 风险是在多种因素紧密耦合作用下，在系统状态的动态调整和演变过程中产生的，不能以孤立的、静态的视角进行风险分析。

针对以上问题，宫培松[4]在系统动力学框架内提出了风险能量、风险流和耦合节点的概念，探讨了多因素耦合作用对地铁车站施工风险的影响；王帆[5]整合了混合相关向量分类机、贝叶斯网络和系统动力学方法，建立了地铁施工安全风险动态演化模型；许慧等[6]、朱敬宇等[7]、吴贤国等[8]采用N-K模型分别分析了城市轨道交通运营风险、深水井喷风险和地铁施工安全风险中“人、机、环、管”4大类因素耦合效应的强度；徐涛[9]在采用N-K模型和耦合度模型分析了水下隧道盾构施工风险因素耦合规律的基础上，采用系统动力学仿真研究了耦合效应对风险水平发展趋势的影响；江新等[10-11]、刘清等[12]采用系统动力学分别对三峡大坝通航风险和水电工程项目群施工风险演变过程进行了分析；孟祥坤等[13]、赵贤利等[14]采用复杂网络理论分别分析了海底管道泄漏风险和机场飞行区风险的演变路径。

上述研究为揭示风险的多因素耦合演变规律做出了有益的探索，但缺少对耦合演变形成机制的系统分析和深入探讨；且研究涉及的耦合系数、耦合度等重要参量不具备明确的物理或统计学意义，难以实际应用。针对上述问题，本文从分析城市地下大空间工程的特点入手，从系统的角度剖析城市地下大空间施工风险的特征，提出一套匹配于施工风险形成机制的风险多因素耦合演变分析方法，旨在揭示城市地下大空间施工重大风险形成机制及关键环节，以期为城市地下大空间安全、经济、高效施工提供参考。

1 城市地下大空间施工风险系统分析

1.1 城市地下大空间的定义

城市地下大空间，是指城市行政区域内地表以下，在工程风险和成本可控的开发深度范围内，为满足特定生产、生活及防灾需求，修建的结构跨度大或具有一定规模的单体地下大空间或网络化地下空间[15]。

1.1.1 单体地下大空间

单体地下大空间根据施工方法不同分为明挖单体地下大空间和暗挖单体地下大空间。明挖单体地下大空间一般是采用明挖法施工的地下综合体、地铁车站或高层建筑基坑等深大基坑工程；暗挖单体地下大空间一般是暗挖车站或类似规模的大跨暗挖工程。单体地下大空间的具体定义见表1，周边环境设施重要性等级划分见表2，工程影响区定义见表3。

表1 单体地下大空间定义Table 1 Definition of monoblock large underground space

表2 周边环境设施重要性等级Table 2 Importance level of surrounding environmental facilities

表3 工程影响区定义Table 3 Definition of project influence area

1.1.2 网络化地下空间

网络化地下空间是指在既有地下空间的基础上，通过零距离近接、连通接驳、竖向增层、以小扩大、多维拓展5类拓建方法形成的平面相连、上下互通的网络化地下空间。网络化地下空间的具体定义见表4。

表4 网络化地下空间定义Table 4 Definition of networked underground space

1.2 城市地下大空间施工风险系统的概念及特征

1.2.1 概念

风险系统是与诱发风险的行动相关联的自然或社会系统的一个抽象概念。风险系统包含风险源、风险事件、风险因素和致险路径，也包含着与这些概念相关的物理实体。

1.2.2 特征

1)风险源众多，风险多样化。城市地下大空间施工中的以下特点导致其施工风险多样，风险源众多。①城市地下大空间施工流程复杂，对施工方法、工艺、施工团队和施工管理水平的要求极高，施工过程的容错率低； ②城市地下大空间多建于城市核心区域，人口密度大，建筑物及市政管线密集，周边环境具有脆弱性； ③城市地下大空间工程一般是受到社会多方关注的关键性工程，任何疏漏都易导致极为不利的社会影响和信誉损失。

2)成险机制复杂。导致城市地下大空间施工风险成险机制复杂的主要原因有： ①城市地下大空间的施工力学机制复杂，许多城市地下大空间的设计具有领先性、独创性，难以基于传统理论和经验分析其成险机制； ②城市地下大空间的施工需要多方协同，使得人的不安全因素影响十分复杂； ③城市地下大空间施工过程中的风险因素间具有普遍的关联性和相对性，使得风险分析变得十分复杂，且难以把握分析的边界。

3)风险因素难以穷尽。风险因素由风险源及成险机制共同决定，因此，城市地下大空间的施工风险因素势必是极其复杂且难以穷尽的。对城市地下大空间施工风险系统的分析一定要把握好分析粒度(即将问题在逻辑上拆分至怎样的细节)以及分析边界(即哪些要素需要考虑，哪些要素不必考虑)等问题。

1.3 城市地下大空间施工风险系统结构

1.3.1 城市地下大空间施工风险子系统

由城市地下大空间施工风险系统的特点出发，可将城市地下大空间施工风险系统划分为工程结构系统、环境系统和组织管理系统3个子系统，如图1所示。

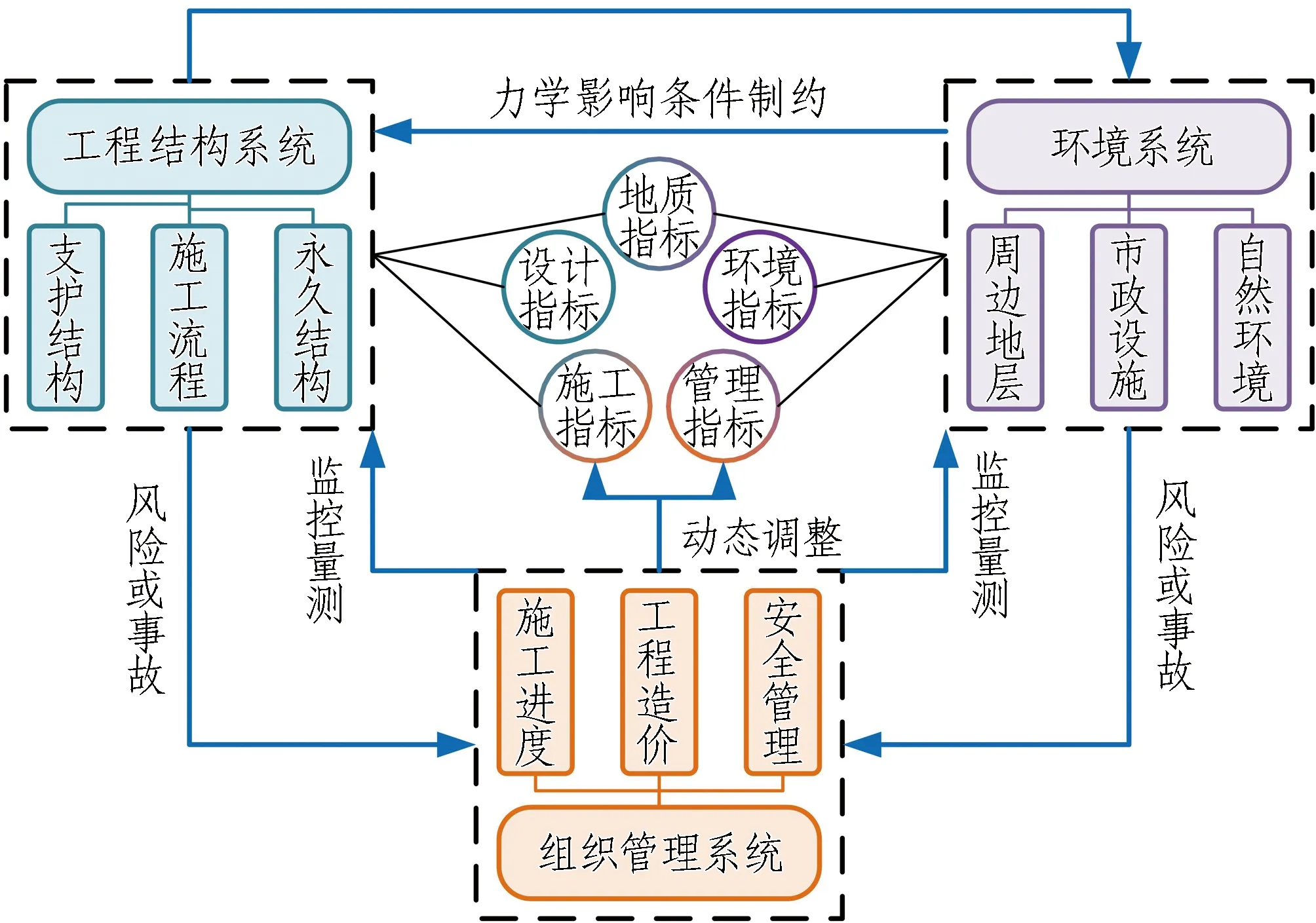
图1 城市地下大空间施工风险系统结构示意图Fig. 1 Structure diagram of risk system in urban large underground space construction

1)工程结构子系统包含： ①以实现城市地下大空间功能为目的的永久结构物； ②为在城市地下大空间施工过程中稳定地层、提供作业空间而修建的永久或临时支护结构； ③施工流程，指为完成城市地下大空间永久结构而必须采取的一系列工法、工序。

2)环境子系统包含： ①地层，包括与城市地下大空间工程施工具有力学联系的地层及水系； ②市政设施，包括工程周边一定范围内的既有建筑物或构筑物； ③自然环境，包括工程周边一定范围内的地形地貌、自然景观等实体，也包括工程区域内的气候、温度、湿度等自然状态； ④社会环境，指城市地下大空间工程所处的周边社区环境、社会舆论环境等抽象实体。

3)组织管理子系统是刻画施工管理行为对施工过程的影响的系统。组织管理子系统由一系列变量及其相互关系构成，这些变量既包含可定量描述的物质变量，如材料要求、安装进度等，也包含难以定量描述的软变量，如政策决策的影响、组织机构合理性等。

1.3.2 城市地下大空间施工风险子系统间的关系

一方面，在施工过程中，工程结构子系统通过力学作用等形式对环境子系统施加影响；另一方面，环境子系统对工程结构子系统有着制约作用，环境子系统的状态决定了工程结构的特性及施工方法。而组织管理子系统通过监控量测收集工程结构子系统和环境子系统相互作用过程中的信息，以对下一步施工措施进行动态控制。

工程结构子系统与环境子系统由施工力学过程主导，体现着系统中具有客观性的一面，因此，又可将两者统称为施工力学子系统；组织管理子系统由人的行为主导，体现着系统中具有主观性的一面。

2 城市地下大空间施工重大风险多因素耦合演变模型

2.1 施工力学子系统模型

2.1.1 施工力学子系统的特点

工程结构子系统与环境子系统具备以下特点： 1)系统的所有行为具有明确的物理机制，理论上可以反复出现； 2)系统中的变量具有明确的物理意义，且可通过计算或测量得出； 3)系统的行为可以定义为一系列具体的事件，可在事件之上定义概率； 4)系统内各层事件之间具有确定的因果关系。因此，可采用基于概率的方法对系统的行为进行量化分析。

2.1.2 施工力学子系统模型结构

根据上述特点，建立如图2所示的施工力学子系统模型。模型总体上分为事件空间和状态空间2个部分。

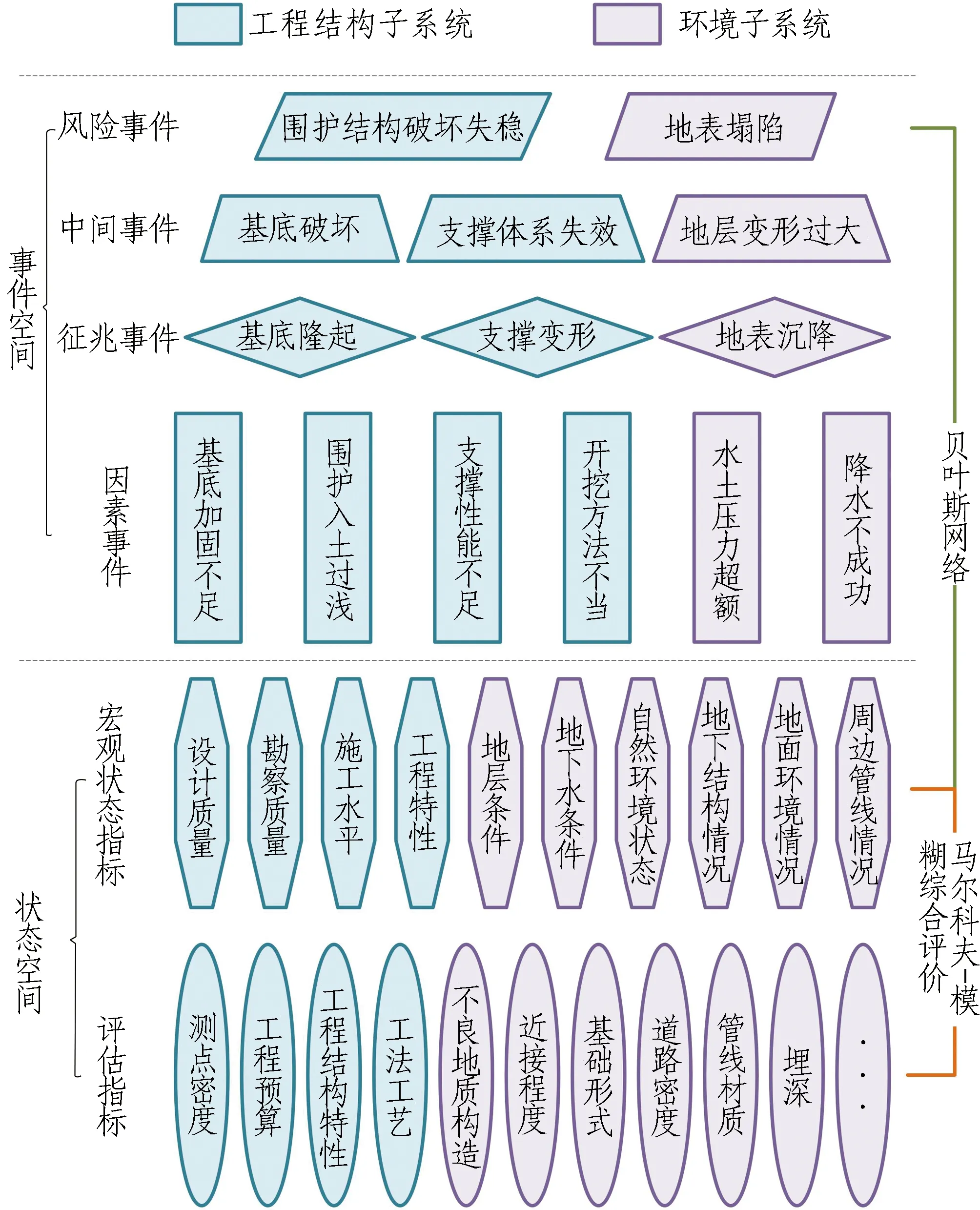
图2 施工力学子系统模型示意图Fig. 2 Model diagram of construction mechanics subsystem

2.1.2.1 事件空间

事件空间中的元素是具有明确定义的事件(event)，相关变量为事件发生的概率，事件间由因果关系相联系。事件空间中包含风险事件层、中间事件层、征兆事件层和因素事件层4级元素。

1)风险事件层。其位于事件空间顶层，其中，元素为风险事件，是风险分析的目标。

2)中间事件层。中间事件指风险形成路径上必要的事件节点，起承上启下作用。

3)征兆事件层。征兆事件的主要意义在于定义了一种对中间事件的观测方法。

4)因素事件层。因素事件又称事件型因素，是发生概率较高但发生后影响较小的“小事件”。

2.1.2.2 状态空间

状态层中的元素是指标(indices)。指标是表征系统状态的变量。状态层中包含宏观状态层和评估指标层2级元素。

1)宏观状态层。宏观状态层中包含设计质量、勘察质量等涵盖城市地下大空间施工风险各方面因素的10个指标。宏观状态指标是包含着大量信息的总括性指标，需要通过概念更具体、更具有可操作性的评估指标来对其间接赋值。

2)评估指标层。评估指标服务于宏观状态指标，是一些需要通过观测、计算或评价得出的具有明确涵义和取值方法的变量。

2.1.3 施工力学子系统分析方法

采用贝叶斯网络和马尔科夫-模糊综合评价法作为施工力学子系统风险分析方法。事件空间中的风险事件、中间事件、征兆事件、因素事件连同状态空间中的宏观状态指标一起构成贝叶斯网络；马尔科夫-模糊综合评价法作为联系评估指标与宏观状态指标的纽带，实现贝叶斯网络的动态输入。

2.1.3.1 贝叶斯网络与风险多因素耦合系数

风险因素的耦合，是指2个以上风险因素同时出现时，由于各风险因素的作用在物理层面上产生相互影响，从而引发的对风险的增幅或抑制作用。风险多因素耦合系数是为度量这种耦合效应的强弱而提出的。

1)双因素耦合模型。图3(a)所示为贝叶斯网络模型中的一个最简化局部，称为基本单元。图中所有节点均为二态节点，代表某一事件。节点R1和R2为节点C的父节点，即C的因素事件。当R1和R2对于C的因果机制独立时[16]，可将图3(a)转化为图3(b)所示的模型。图3(b)中，ξ1，ξ2为与C具有共同状态空间的随机变量；“∨”为逻辑“或”合成算子。此时，关于C的条件概率可表达为

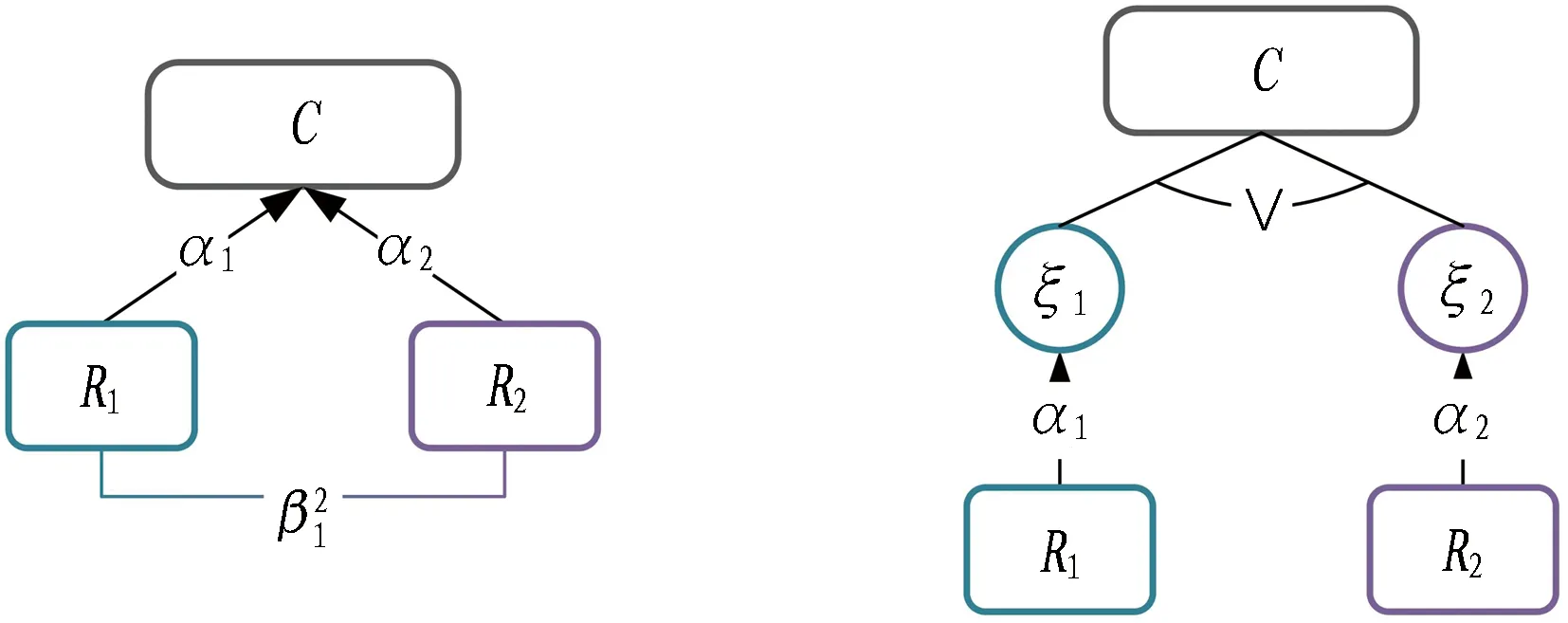
(a) 双因素耦合原始模型(b) 双因素耦合等价模型图3 双因素耦合模型示意图Fig. 3 Schematic of dual-factor coupling model

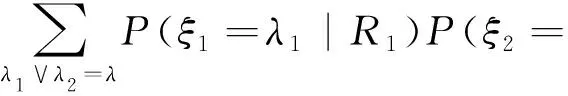
λ2|R2)。

(1)

式中：P(ξi=λi|Ri)为Ri对C的贡献概率分布；λi∈{True, False}，εi=True代表事件εi发生，εi=False代表事件εi不发生，下文记εi=T或εi=F。

根据因素事件的定义，可假定P(ξi=T|Ri=F)=0，即因素事件不发生时对结果事件的发生概率不产生影响。在这一假定下，图3(a)所示贝叶斯网络节点C的条件概率表(CPT)便可根据式(1)由2个条件概率P(ξi=T|Ri=T)=αi表达。

(2)

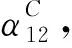
(3)

表5 耦合系数取值表Table 5 Value reference of coupling coefficient

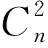
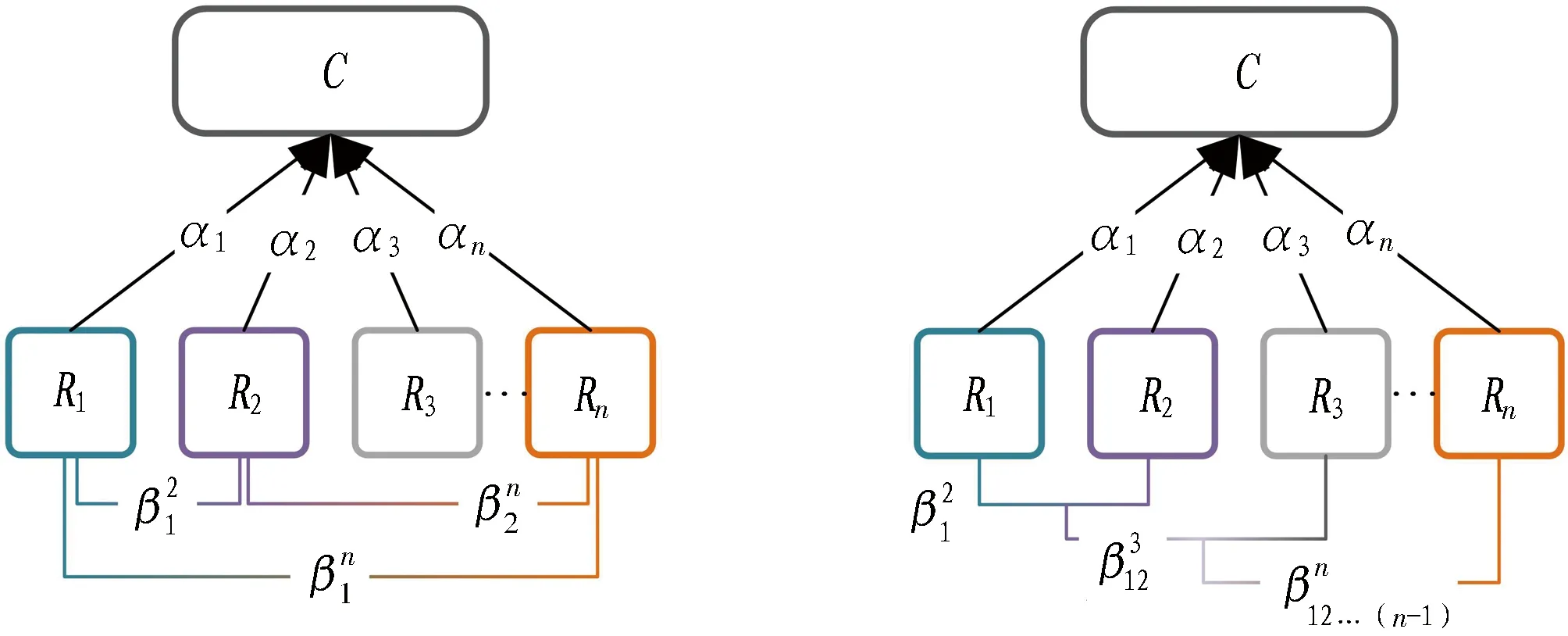
(a) 多因素耦合原始模型 (b) 多因素耦合树图4 多因素耦合模型示意图Fig. 4 Schematic of multi-factor coupling model

为解决这一问题，在处理多因素耦合的情况时，认为耦合作用是以“耦合树”的形式，按一定顺序逐层作用的。如图4(b)所示，耦合作用首先在R1和R2间产生，随后逐个与R3，R4，…，Rn作用，表达为

(4)

(5)

需要指出的是，同一个问题中“耦合树”不是唯一的，耦合树的选取会对分析结果产生一定影响，在实际操作中应尽量将耦合效应强烈的因素对置于耦合树的下层。

2.1.3.2 马尔科夫-模糊综合评价

马尔科夫-模糊综合评价法是将随机过程理论中的马尔科夫链与模糊综合评价法进一步融合建立的，可在一定时间序列上对被评价问题进行预测。

设问题的论域U为包含m个元素的离散集合，因素集V中包含n个元素，时间序列由离散指标t=0,1,2,…表示。在初始时刻(t=0)，各因素对论域的隶属度向量

(6)

对隶属度向量归一化：

(7)

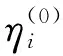
根据模糊统计与概率统计之间的关系，归一化的隶属度可视为因素处于论域中各状态的主观概率。设该因素在时间维度上受某一马尔科夫链调控(论域U即为马尔科夫链的状态空间)，那么该因素在任意时刻的状态分布可由马尔科夫链表达为

(8)

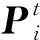
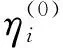
(9)

2.2 组织管理子系统模型

2.2.1 组织管理子系统的特点

组织管理子系统主要体现着人的不确定因素，这一系统有着与力学系统截然不同的特点，如下： 1)系统的行为仅存在逻辑上的联系，很难与物理机制挂钩。2)系统中的变量众多，且各变量的状态具有极大的不确定性。即便在相对一致的外部条件下，系统的行为也很难复现。3)系统的行为一般仅能以其宏观状态的变化来描述，难以采用事件的形式进行定义，因此也难以采用概率的方法去度量系统的响应。4)系统内各环节的相互关系错综复杂，因果关系交织，即便通过逻辑推演得出系统结构，也难以直观预测系统的行为。

2.2.2 组织管理子系统分析方法

组织管理子系统采用系统动力学(system dynamics，SD)作为风险分析方法。SD理论由美国麻省理工学院的Forrester教授于20世纪50年代提出[17]。SD基于系统论、控制论与信息论，从系统内部控制机制和结构出发，着重研究系统机构与其功能行为的动态关系，是对具有复杂非线性多重反馈机制的系统进行定性和定量分析的有效方法。

城市地下大空间SD建模步骤如下。

1)确定系统边界。建模的首要任务是确定系统内的要素和变量。组织管理子系统包含组织机构、现场管理、人员素质及工程合同等若干状态集，而系统状态的变化体现为施工质量、施工成本和施工进度3个相互间具有约束关系的绩效指标的变化，并以此影响施工力学子系统的行为。

2)分析因果关系。系统边界确定后，需要分析主要变量间的因果关系，确定其传递极性，绘制因果回路图(见图5(a))。城市地下大空间施工组织管理子系统包含以下4个主要回路：

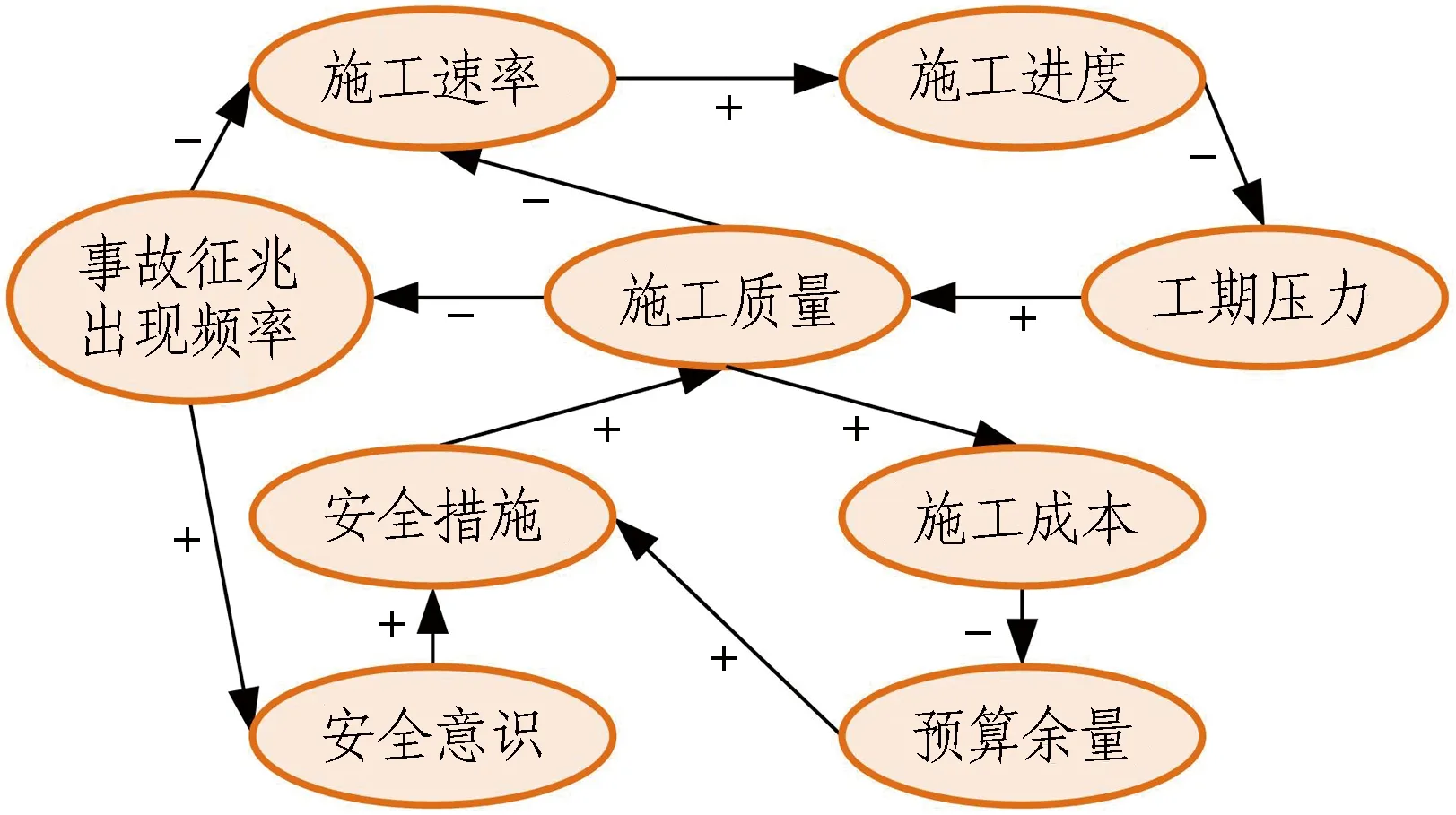
(a) 因果回路图

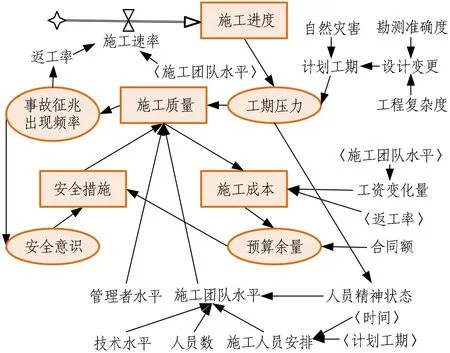
(b) SD存量流量图图5 城市地下大空间组织管理子系统SD模型Fig. 5 Modeling procedure of system dynamics

①施工速率—施工进度—工期压力—施工质量回路；

②施工质量—施工成本—预算余量—安全措施回路；

③施工质量—事故征兆出现频率—安全意识—安全措施回路；

④施工质量—事故征兆出现频率—施工速率—施工进度—工期压力回路。

3)建立存量流量图。在因果回路图的基础上，补充存量、流量、辅助变量、外生变量和参数，建立包括模型内所有关系的SD存量流量图(见图5(b))。城市地下大空间施工组织管理子系统模型以施工进度作为唯一的存量变量，以施工速率作为与施工进度相关联的率变量。组织管理系统状态随着施工进度的推进而自发演变，并在工期压力、施工质量、施工成本和安全措施之间的反馈关系支配下动态调整。

4)建立方程。根据SD存量流量图建立系统动力学方程，并为方程中的参数赋值。

5)仿真模拟。进行模拟仿真，调试并修正模型，得到输出结果。

3 应用案例

3.1 工程概况

3.1.1 工程背景

北京地铁17号线东大桥站为与既有6号线的换乘站。东大桥站位于东大桥路、工人体育场东路与朝阳门外大街、朝阳北路相交的五叉路口，其平面位置如图6所示。车站总长336.8 m，总建筑面积为24 590.9 m2。车站标准段为暗挖双层双柱3跨结构(宽24.5 m)，下穿区段为暗挖单层单洞结构(长36.5 m)，北端为暗挖双层3柱4跨结构(长49.7 m)。车站结构高17.85 m，中心里程处单层结构覆土约15.18 m，有效站台中心处底板埋深约33.6 m。

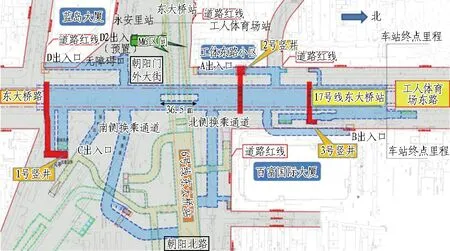
图6 东大桥站平面位置示意图Fig. 6 Plane position of Dongdaqiao station

3.1.2 工程地质与水文地质

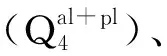
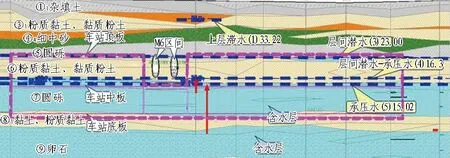
图7 东大桥站地质剖面图(单位: m)Fig. 7 Geological profile of Dongdaqiao station (unit: m)

站址区地下水主要可划分为上层滞水、层间潜水、层间潜水—承压水和承压水。地下水主要补给方式为区域地下水侧向径流及来自上部的垂直渗透，以径向侧流方式排泄。

3.1.3 场地及周边环境

车站周边为成熟社区和商业、商务区，地面车流量大，交通繁忙。车站与既有6号线东大桥站及区间隧道距离较近，最小水平净距3.14 m，最小垂直净距1.68 m。车站范围内市政管线众多，管径300～1 750 mm，还存在多条热力方沟、雨水方沟及电力隧道。

3.1.4 施工方法

车站主体采用暗挖洞柱法施工。导洞断面为拱顶直墙平底结构，上、下导洞开挖宽度为4.7 m，高度为5.5 m，采用台阶预留核心土法施工。导洞临近既有区间段10 m范围内采用深孔注浆超前加固地层，导洞端头打设导管注浆加固。车站采取降水措施进行无水暗挖作业。

3.2 风险分析模型建立

3.2.1 风险分析单元划分

1)空间维度划分。北京地铁17号线东大桥站总长约330 m，最大宽度约33 m。根据东大桥站的结构特点，将车站在其水平投影上划分为东南(SE)、东北(NE)、西南(SW)、西北(NW)和中央(C)5个区域，如图8所示。

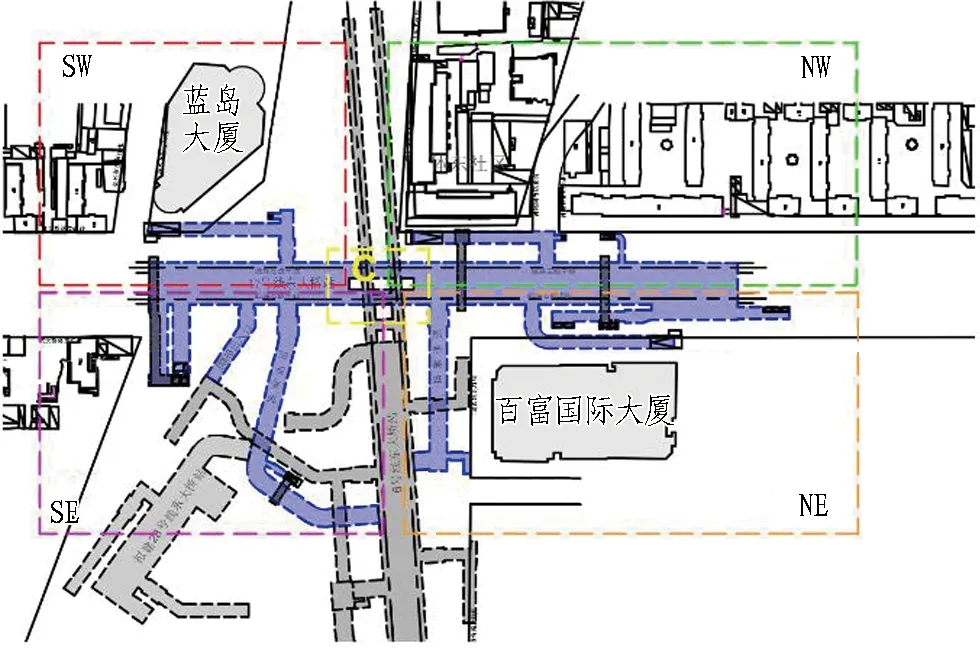
图8 东大桥站工程分区示意图Fig. 8 Schematic of partition scheme of Dongdaqiao station

2)时间维度划分。北京地铁17号线东大桥站属于网络化拓建工程，根据工程特点，将工程按工程分项和主要工序在时间维度上划分为13个分块，如图9所示。

图9 东大桥站风险分析单元划分(时间维度)Fig. 9 Risk analysis unit division of Dongdaqiao station (time dimension)

3.2.2 贝叶斯网络模型建立

3.2.2.1 贝叶斯网络结构

北京地铁17号线东大桥站施工风险贝叶斯网络模型见图10。模型中共有29个节点，其中包含5个顶层风险事件节点、3个中间事件节点、11个因素事件节点和10个宏观状态节点。

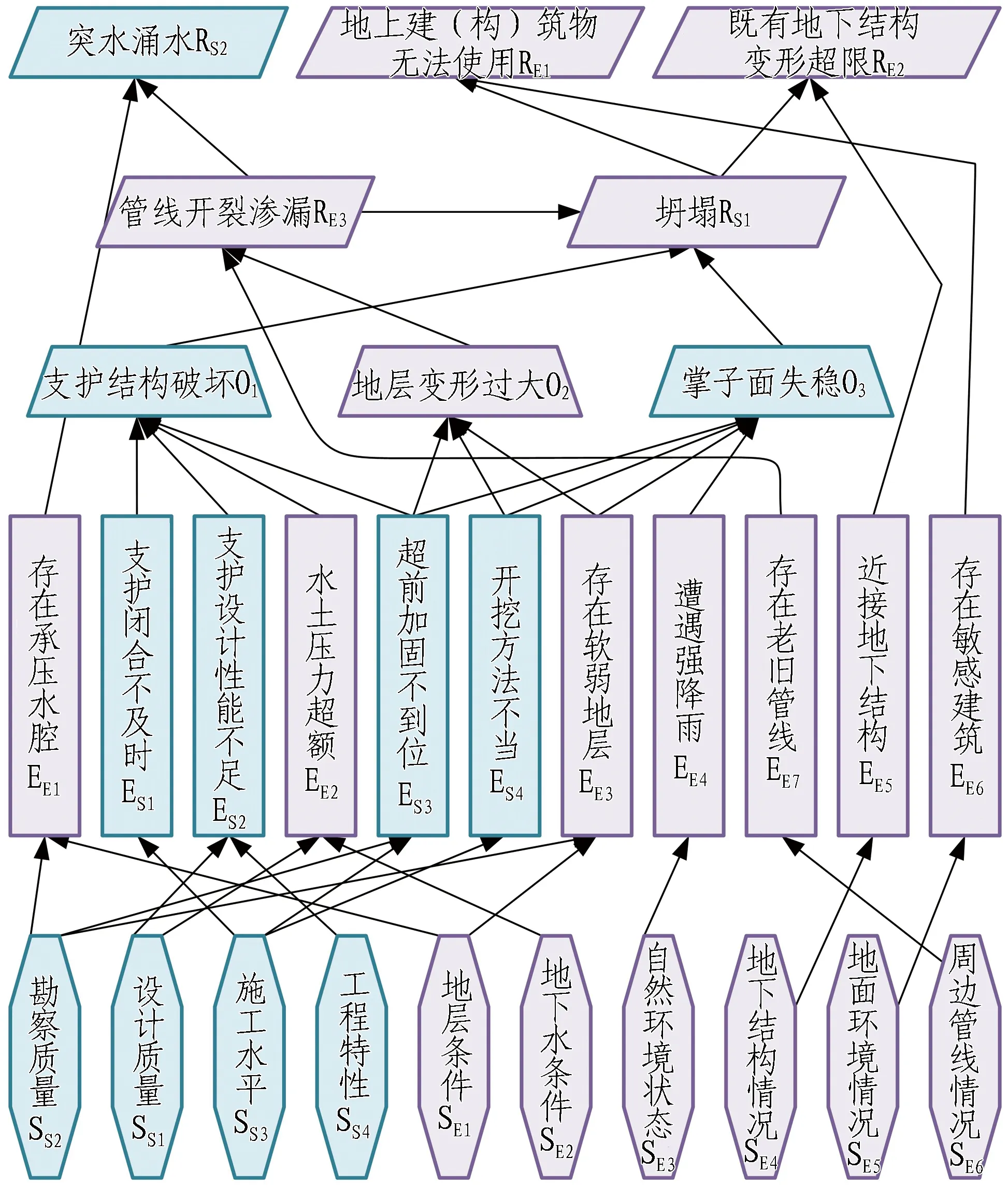
图10 东大桥站施工风险贝叶斯网络模型Fig. 10 Bayesian network model of construction risk in Dongdaqiao station

3.2.2.2 耦合因素分析

通过会议讨论和专家咨询，确定东大桥站施工风险系统中存在以下4组耦合因素对。

1)超前加固不到位-存在软弱地层(ES3-EE3)。当地层性质较差时，不合格的超前加固极易导致开挖面在支护结构架设之前发生失稳。显然，该因素对的耦合会对风险产生增幅作用，耦合极性为正耦合。一般来说，该因素对中任一方单独出现均不足以导致较大的风险，但两者若同时出现则可能诱发灾难性的事故。因此，判定该因素对为“强耦合”。

2)支护设计性能不足-存在软弱地层(ES2-EE3)。软弱地层基本不具有自承能力，支护结构需要独自承担施工期的大部分荷载。在2007年巴西圣保罗地铁皮涅罗斯车站隧道坍塌事故中[18]，由倒悬岩脊形成的巨大荷载作用于性能不足的支护结构，导致隧道瞬间坍塌。因此，判定该因素对为“强耦合”。

3)遭遇强降雨-存在软弱地层(EE4-EE3)。软弱地层通常具有更差的水理特性，在强降雨的作用下会进一步软化。该因素对是多起地下工程施工事故的重要诱因，故判定其耦合强度为“极强耦合”。

4)支护设计性能不足-支护闭合不及时(ES2-ES1)。“强支护、快封闭”作为浅埋暗挖法十八字方针中的重要部分常被一同提及，说明这2个因素存在显著的耦合效应。但在不考虑其他因素的情况下，该因素对的耦合效应不至于使风险产生较大增幅，故判定其为“中耦合”。

东大桥站施工风险因素耦合树见图11。各耦合因素对的耦合效应评级及耦合系数取值见表6。

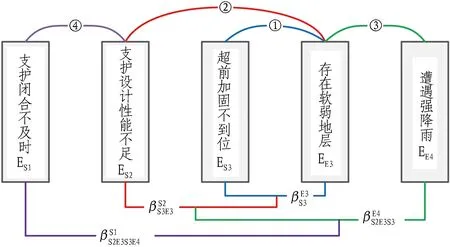
图11 东大桥站施工风险因素耦合树Fig. 11 Coupling tree of construction risk factors of Dongdaqiao station

表6 东大桥站各耦合因素对的耦合效应评级及耦合系数取值Table 6 Risk factor coupling effect evaluation form of Dongdaqiao station

3.2.2.3 条件概率表(CPT)

1)中间事件及风险事件节点。模型中各事件节点间的贡献概率分布见表7。中间事件及风险事件节点的CPT可通过式(1)、式(3)、式(4)、式(5)及表6中的耦合系数计算得到。

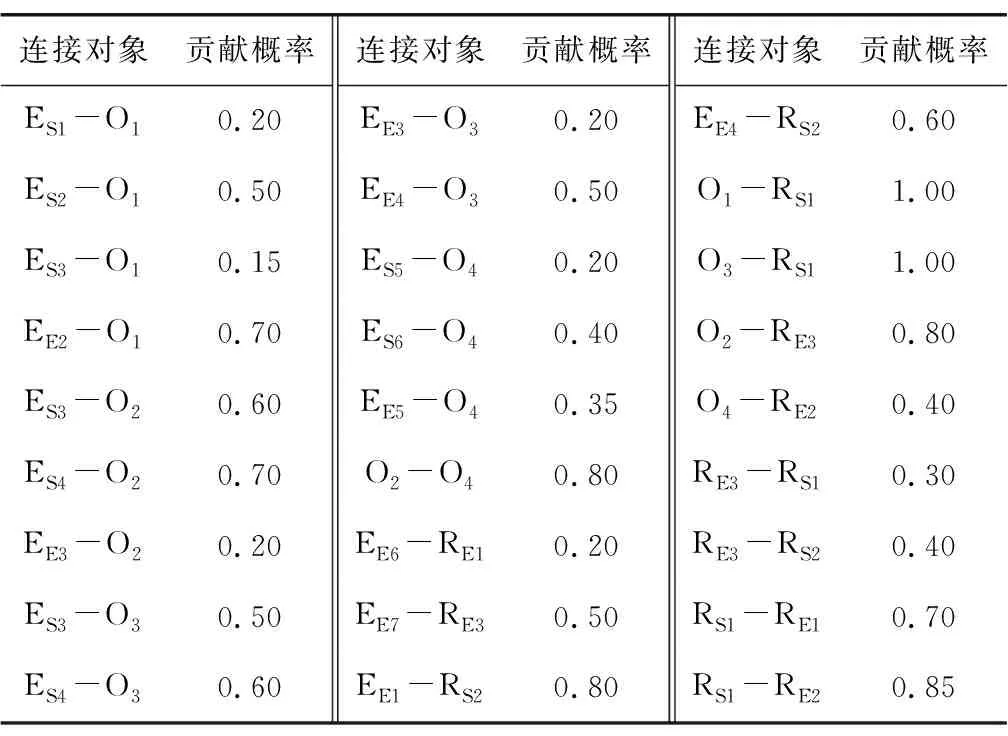
表7 事件节点间的贡献概率分布Table 7 Contribution probability distribution between event nodes

2)因素事件节点。因素事件节点上的条件概率通过式(10)计算。

(10)

(11)

本模型中宏观状态指标的状态数统一为4个，状态1代表最不利状态。宏观状态指标与因素事件间的贡献强度系数取值见表8。

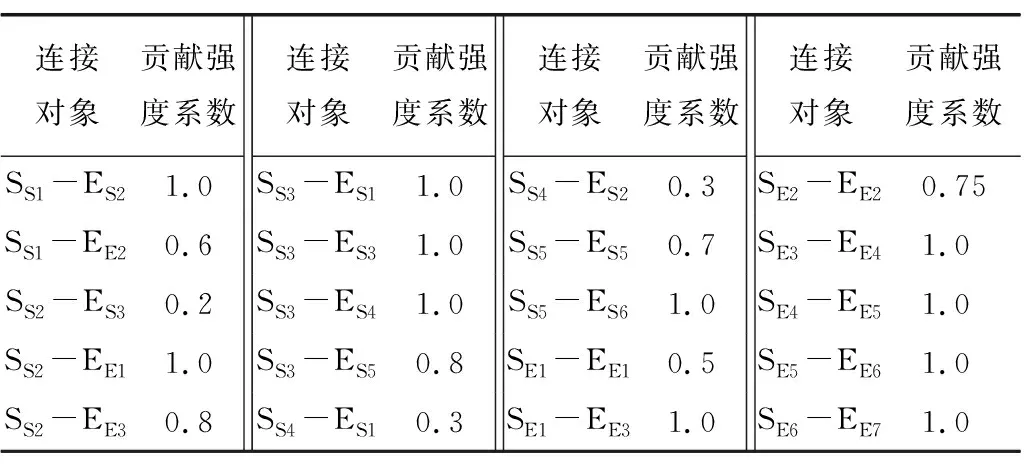
表8 宏观状态指标与因素事件间的贡献强度系数取值表Table 8 Contribution intensity coefficient values

3.2.3 评估指标及权重

各宏观状态指标对应的评估指标、隶属度及权重见表9。

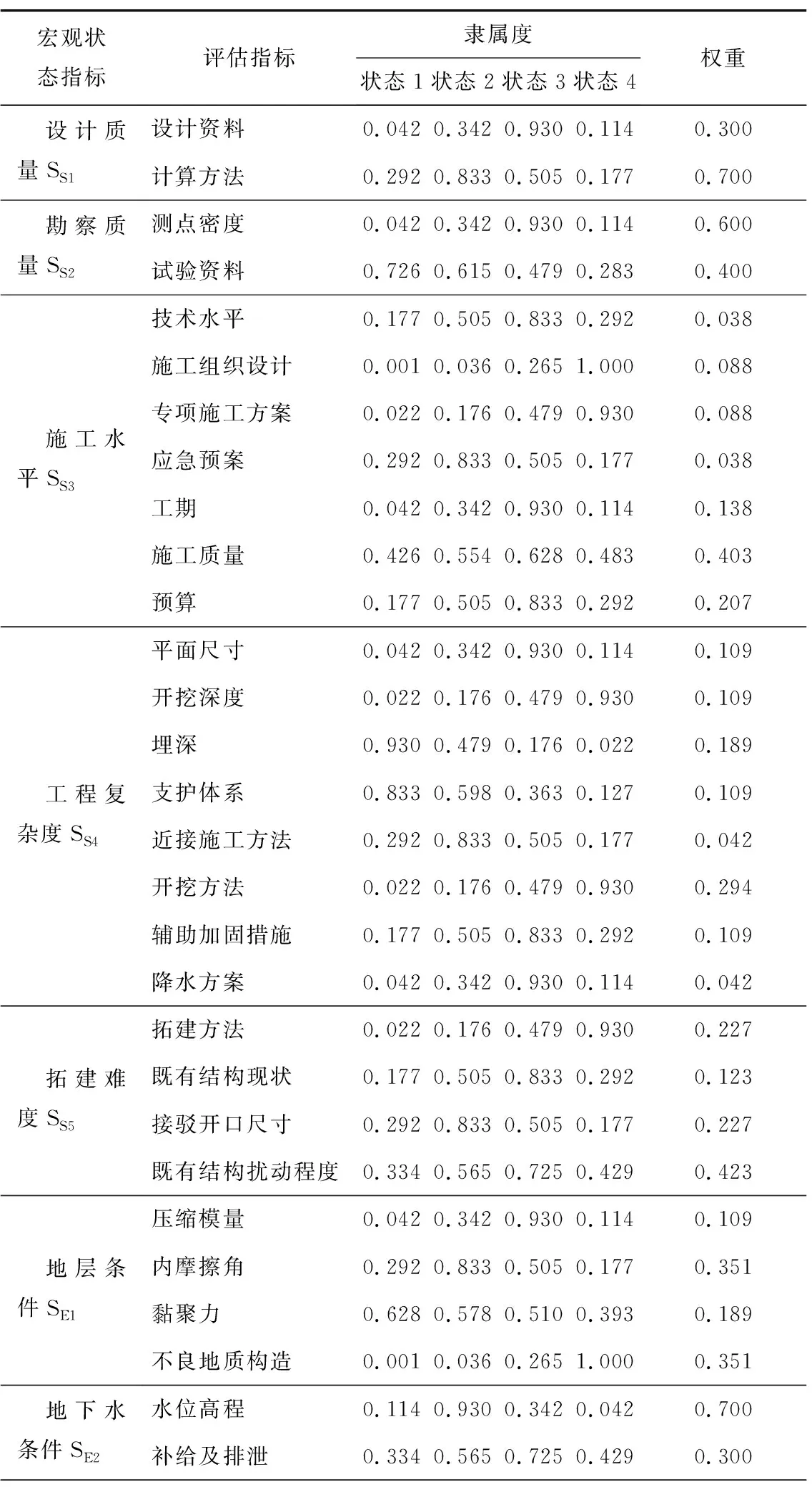
表9 各宏观状态指标对应的评估指标、隶属度及权重Table 9 Evaluation index membership degree and weight

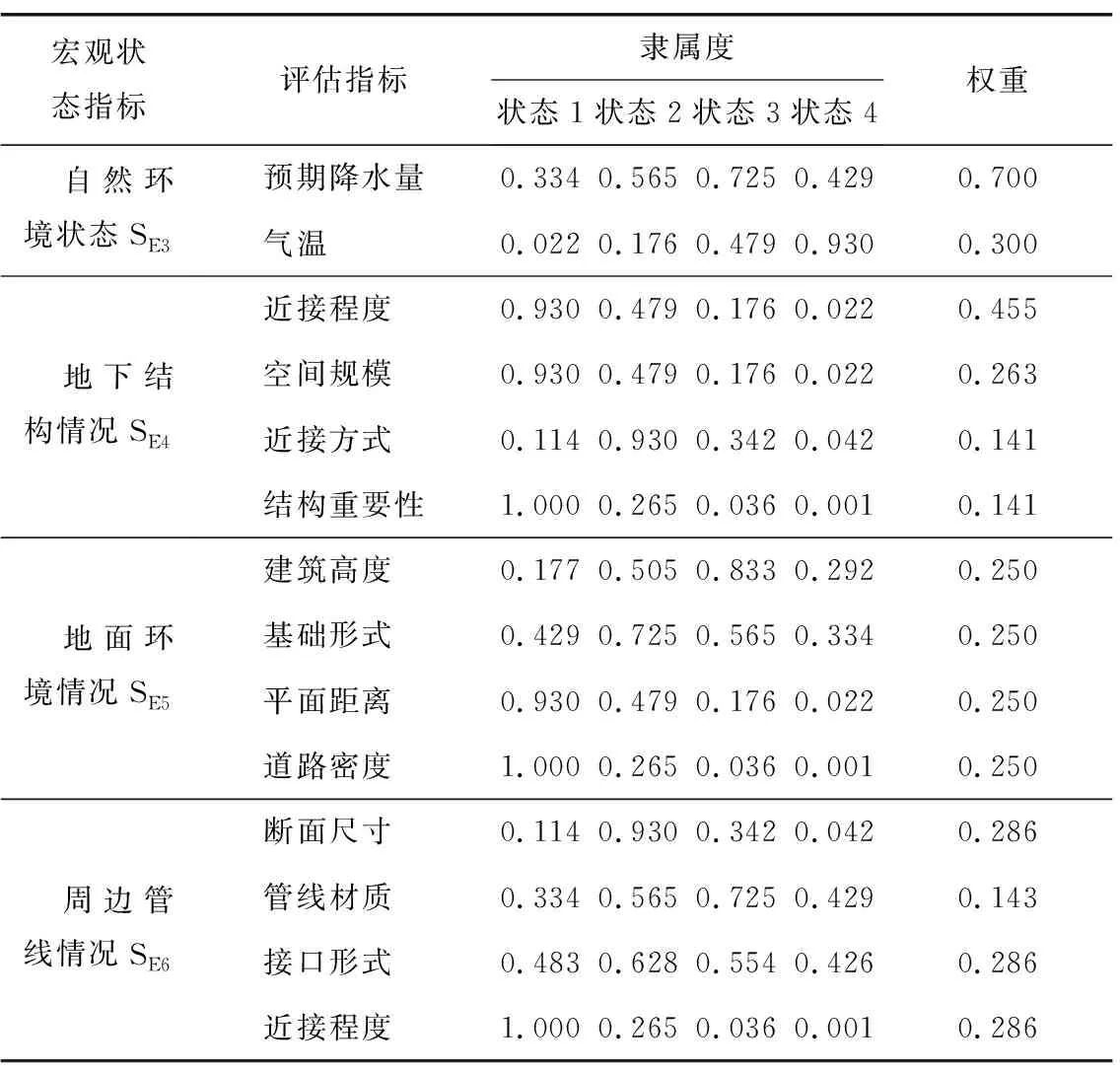
表9(续)

3.3 结果分析

3.3.1 施工过程风险等级与演化规律分析

根据施工组织计划，东大桥站自竖井开挖施工至内部结构浇筑完毕计划工期2年10个月。本次分析时间跨度按150周考虑，分析时间步长为1个自然周。通过马尔科夫-模糊综合评价和系统动力学仿真得到评估指标的时间历程数据后，导入贝叶斯网络进行分析，结果如图12所示。

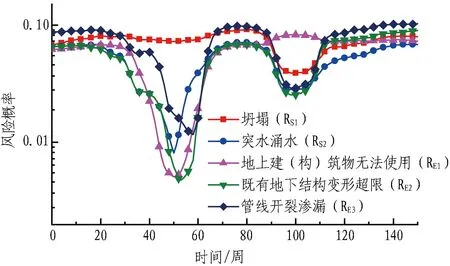
图12 东大桥站风险分析结果Fig. 12 Risk analysis results of Dongdaqiao station

分析结果表明，东大桥站施工过程中主要风险事件发生概率为0.06～0.09。根据GB 50652—2011《城市轨道交通地下工程建设风险管理规范》规定，风险发生可能性等级为2级，风险等级根据风险事件不同为Ⅰ级或Ⅱ级。施工过程中风险具有阶段性特征，各风险事件发生概率在开挖阶段较大；在竖井开挖后约35周进入钻孔灌注桩施工阶段后以及于约90周主拱二次衬砌施作完成后，各风险事件的发生概率有不同程度的降低。分析结果符合工程经验认知。

3.3.2 风险因素耦合效应影响分析

表10示出了考虑风险因素耦合效应、不考虑某一对风险因素的耦合效应和完全不考虑耦合效应时的风险事件最大发生概率。从表中可以看出，风险因素耦合效应对风险事件发生概率具有较为显著的影响。在本案例中，“超前加固不到位ES3”和“存在软弱地层EE3”的耦合效应影响最广，而“遭遇强降雨EE4”和“存在软弱地层EE3”的耦合效应影响最大。在分析的5个风险事件中，“坍塌RS1”、“地上建(构)筑物无法使用RE1”和“既有地下结构变形超限RE2”受耦合效应影响明显，考虑耦合时的发生概率相较于不考虑耦合时的发生概率分别提高了0.019 5、0.011 2和0.012 2。在现行的风险分级标准体系下，1%的风险发生概率偏差已足以导致对风险等级的错误估计，进而影响施工方对风险处置策略和施工方案的决策，甚至可能成为事故的导火索。可见，对于城市地下大空间施工这类复杂的过程，在风险评估中考虑耦合效应的影响十分必要。

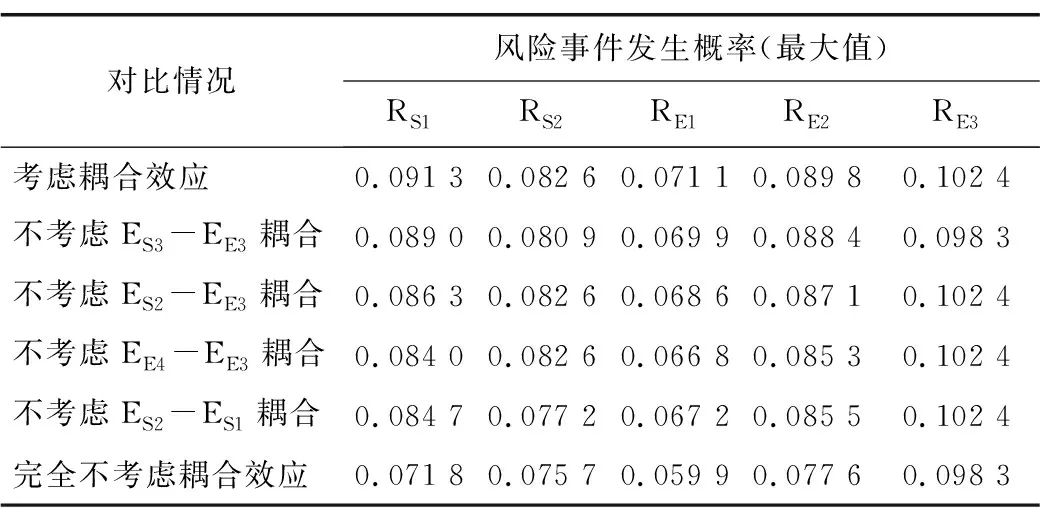
表10 风险事件最大发生概率Table 10 Influence of risk factor coupling effect on probability of risk events

4 结论与讨论

1)城市地下大空间的施工是一个复杂的系统化工作，因此，需要以系统的角度分析其施工风险。城市地下大空间施工风险系统可分为工程结构、环境和组织管理3个子系统。工程结构子系统和环境子系统是由力学机制主导的事件驱动型系统，适合采用贝叶斯网络结合模糊综合评价法进行分析；组织管理子系统是一个抽象系统，适合采用系统动力学进行分析。

2)城市地下大空间施工风险系统的复杂性决定了其风险因素间的耦合效应普遍存在，且不可忽略。通过在贝叶斯网络框架中引入风险因素耦合系数的概念，可对耦合效应作出合乎逻辑的定量化描述，同时也可简化贝叶斯网络的构建过程。

3)通过马尔科夫链理论和模糊综合评价法的结合，可将风险分析工作拓展至时间维度上，对施工过程中的风险演变趋势进行预测；另外，系统动力学可对组织管理系统的内生性动态行为进行模拟，较为真实地反映出工程管理组织行为的动态变化对施工风险的影响。

4)以北京地铁17号线东大桥站为依托，对城市地下大空间施工重大风险耦合演变模型进行了实际运用。结果表明，城市地下大空间施工风险具有明显的阶段性特征，在开挖阶段达到最大；风险因素耦合效应对风险事件发生概率具有显著影响，忽略风险因素的耦合效应会使风险分析结果出现较大偏差。

本文在城市地下大空间施工风险分析理论及风险多因素耦合演变效应的研究方面取得了一定的成果，但仍有许多问题值得进一步研究。目前，对风险耦合演变效应的理解仍处在“灰箱”阶段，仅能通过表观现象和结果进行推测。在今后的工作中，需要对风险耦合演变机制进行更深入的研究，并结合工程实践不断完善其理论框架、研究方法和量化标准。此外，本文提出的理论和模型较为复杂，难以在实际工程中推广，如何以本文研究为基础，提炼出一套更加实用、易用的施工风险评估体系，也是一项值得探讨的问题。