共享电动汽车系统车队规模与停车泊位数优化

马舒予，胡 路，吴佳媛，刘 珺

（1.西南交通大学，交通运输与物流学院，成都 611756；2.综合交通大数据应用技术国家工程实验室，成都 611756）

0 引言

随着私家车保有量的不断增加和环境污染问题日益严重，环保、便捷的汽车共享模式成为交通领域的研究热点[1]。汽车共享模式不但可以减轻因过度拥有汽车而引起的交通拥堵、资源消耗和环境污染问题，同时还可以为用户分担车辆购买等相关费用，具有重要的实践推广价值[2-3]。目前，汽车共享模式发展迅速，EVCARD、GoFun 等共享汽车运营商在国内一二线城市布局设点，效果较好[4]，但许多企业仍处于整合期，面临着诸多挑战。如何更好地模拟汽车共享系统运营过程，解决实际问题，为汽车共享企业决策提供理论支撑仍然具有显著的研究意义。

国内外学者对共享汽车系统优化的研究取得了较为丰富的成果，主要涉及三个层面的决策：规划层面（站点数量和选址）[5-8]、配置层面（车队规模和停车泊位数设计）[9-11]和运营层面(定价和车辆调度策略)[12-21]。Jorge[15]等建立了混合整数非线性规划模型，以运营商利润最大为目标优化动态定价，实验表明使用动态价格可以降低成本、提高共享汽车系统盈利能力，并使各个站点之间的车辆需求保持平衡。在配置决策方面，Hu[9]等运用混合排队网络理论对共享汽车系统建模，在考虑道路拥堵约束的情况下，联合优化了共享汽车系统停车泊位数和车队规模，通过分析不同道路拥堵场景下的优化结果，发现在中度拥堵时系统取得最大利润。Huang[16]等设计梯度算法优化站点选址、停车泊位数和车辆调度，实现了三个层面的联合优化，并提出停车成本是影响企业营利的关键因素。上述研究均是以燃油汽车为研究对象，随着电动汽车的发展，越来越多的运营商开始使用更环保节能的电动汽车。

电动汽车的使用要求考虑车辆有限行驶里程和车站充电问题[17]，这对系统的建模和优化都增加了难度。在目前共享电动汽车系统研究中，往往做出一些假设来满足用户电量需求。Xu[18]等假设车辆在满电状态下才能被用户取走，建立MINLP模型优化车队规模和定价。但他们提出了该假设的缺点，即不必要的充电时间将降低车辆利用率，使得车队规模变大、成本增加。Zhao[19]等根据车辆实时运行状态、充电率和消耗率更新车辆电量，提出基于时空网络的混合整数线性规划模型（Mixed-Integer Linear Programming，MILP），优化车辆调度。Hua[20]等根据电量状态划分车辆，将电量状态处于同一值域的车辆分为一组，对站点选址、车队规模和车辆调度进行联合优化，在优化过程中，电量状态无法满足行程需求的车辆将会被剔除。冉伦[21]等在车辆需求不确定的情况下，基于需求量的均值和方差以最小车辆取走率和返还率为约束，建立了车辆调度优化模型，他指出，在达到一定服务水平后，应增加系统的车辆数和停车位来满足服务水平要求。分析上述研究发现，现有关于共享汽车系统的研究主要集中在调度和动态定价决策方面，而关于配置决策中停车泊位数和车队规模的联合优化甚少，在共享电动汽车系统中尤为明显。

另外，在共享汽车系统中，用户需求、路径选择以及还车需求等因素均呈现动态性（随时间变化）和不确定性（随机性）的特点。这种动态随机环境将造成供给和需求在时空上的不匹配。现有研究中，无论是传统燃油汽车共享系统还是共享电动汽车系统，只有极少数研究构建的模型能够同时兼顾动态和随机两种环境。Hua[20]、Deng[22]等在动态随机环境下，分别对燃油汽车共享系统和共享电动汽车系统车辆调度进行优化。Hu等[23]基于逐点稳态流体逼近方法（Pointwise Stationary Fluid Flow Approximation,PSFFA），将离散个体连续化，提出了流体排队网络模型。流体排队网络模型可以借助时变参数准确刻画系统动态性，同时捕捉系统随机性，有效求解动态网络模型。马媛等[24]通过建立地铁车站通道系统流体排队模型，捕捉系统动态性能并确定适时客流预警阈值。本文基于流体排队网络理论，建立共享电动汽车系统流体排队模型，同时捕捉系统动态性和随机性。

综上所述，国内外学者对共享汽车的系统优化涉及多个层面，但在建立模型时，并没有考虑到共享汽车的引入将导致出行需求的转移，尤其是公交出行需求转移到共享汽车服务需求后对道路拥堵的影响，也没有考虑道路拥堵对用户出行需求的影响，即用户需求与道路拥堵的交互影响。新型交通方式的可持续发展不仅要考虑运营商利益，同时也需要从社会公众利益角度出发，避免加剧城市拥堵；从另一角度看，道路的拥堵往往影响着共享汽车服务出行需求，忽略这一因素，将导致需求产生偏差，无法为运营商提供更有效的决策支撑。

因此，本文考虑用户需求与道路拥堵的交互影响，联合优化动态随机环境下共享电动汽车系统车队规模和停车泊位数。为了更精确地分析共享电动汽车系统，建立动态随机环境下的混合流体排队模型；为描述道路拥堵和定价对用户出行需求的影响，建立非线性弹性需求模型；为考虑用户、运营商和公众三方利益，建立以运营商利润最大为目标，道路拥堵和车站拥堵为约束的MINLP模型；为比较启发式算法和精确算法的优劣性，分别设计遗传算法和MADS 算法求解模型，并分析需求、道路拥堵和定价对共享电动汽车系统优化结果的影响。决策生成的车队规模与停车泊位数可以为共享电动汽车系统配置决策提供理论支撑，保障共享电动汽车服务的可持续发展。

1 共享电动汽车系统模型

以单向式共享电动汽车系统为研究对象：初始时刻车辆分布在各规划站点中，每个站点的车辆数和停车位有限；每个停车位均配备充电设施，以保证车辆在达到车站后可以立即充电；用户可以提前预定或者直接在车站取车，在行程结束后，需将车辆返还到任意车站。本研究基于共享电动汽车大规模普及和广泛使用的场景对系统做出以下假设：（1）任意两个站点之间有且仅有一条路径；（2）用户在车辆充满电后才能将其驶出车站，且所有车辆在初始时刻均处于满电状态；（3）满电状态下的车辆可以满足任意行程的电量消耗需求；（4）车辆在车站所需充电时间与上一次行程里程数相关；（5）系统中的车辆类型为性能相同的电动汽车，所有充电设施具有相同的充电效率，即所有车辆具有相同的充电速度；（6）任意两个站点之间的出行需求受价格和道路拥堵影响，用户可以通过相关软件获取当前道路拥堵信息。符号释义如表1所示。

表1 符号释义Tab.1 Symbol interpretation

续表1

1.1 动态随机环境和流体排队模型

在共享汽车系统中，用户需求、路径选择、行驶时间和还车需求等因素均随着时间而变化，且具有不确定性，更具实际意义的系统建模往往需要考虑这两种特性。结合Hu等[9,23]的研究，我们对运营时间进行离散化，将一天的运营时间划分为多个较小的时间段，由Δ 表示，建立共享电动汽车系统混合流体排队模型。其中时间段Δ取15 min，系统运营时间取6:00～24:00，即一天运营时间总时间段数T=72，第t个时间段表示时刻t到时刻t+ 1的时间段。模型包括共享汽车在车站的排队模型和共享汽车在路径上的排队模型。

1.2 共享电动汽车系统的充电特性

与传统的共享汽车系统相比，共享电动汽车系统涉及车辆在车站充电，本文假设所有车辆必须在充满电的状态下才能驶离车站，在此前提下，各车站内车辆的剩余充电时间影响该车站服务率（单位时间内车站输出车辆数）。为了描述充电对共享电动汽车系统的影响，我们通过车辆行驶里程数更新每一时刻各车站可用共享汽车和不可用共享汽车的平均剩余充电时间，如下所示：

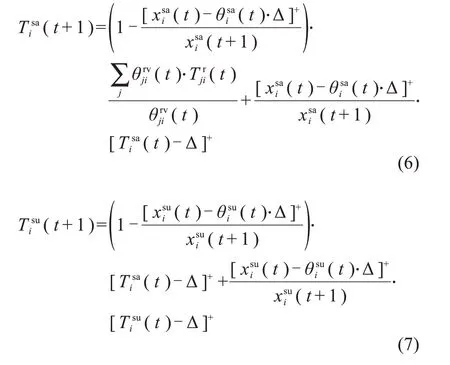
t+1时刻车站i可用共享汽车和不可用共享汽车的平均剩余充电时间来源于两部分。对于可用共享汽车而言，第一部分剩余充电时间为[t,t+1]时段内到达车站i车辆的补给充电时间；第二部分为[t,t+1]时段内没有充满电量的可用共享汽车的剩余充电时间，等于t时刻车站i可用共享汽车平均剩余充电时间减去一个时间段Δ，即[Tisa(t)-Δ]+。对于不可用共享汽车而言，第一部分剩余充电时间为[t,t+1]时段内被新预定的不可用共享汽车的剩余充电时间，这部分不可用共享汽车是从可用共享汽车转变而来，因此，剩余充电时间为[Tsai(t)-Δ]+；第二部分为[t,t+1]时段内没有充满电量的不可用共享汽车的剩余充电时间，等于[Tsui(t)-Δ]+。

1.3 非线性弹性需求模型

为了描述时间和成本对用户出行的影响，本文基于Xu[18]等建立的弹性需求模型，构建了用户出行需求与出行时间（道路拥堵）、出行成本（定价）之间的关系模型，具体表现形式如下：

路径aij上车辆的平均速度vij( )xij(t) 采用Hu[23]等的平均速度模型。平均速度模型揭示了汽车速度与道路拥堵的关系。式（8）表明任意两个站点之间的出行需求受到出行时间和定价的影响，其中，出行时间由道路平均速度决定，当定价pij超过用户所能接受最大定价pmax或道路处于绝对拥堵状态（实际道路占有率等于1）时，用户放弃共享汽车出行服务转向更为经济或时间更短的出行方式，例如地铁等。用户出行需求与时间和成本之间的非线性弹性关系模型反映了在系统定价和道路拥堵影响下，用户实际出行需求dij(t)与用户潜在出行需求Dij(t)之间的差异。值得注意的是，我们可以通过上述非线性弹性需求模型和流体排队网络模型来描述共享电动汽车系统动态随机环境下用户需求和拥堵的交互影响，即用户需求受当前道路拥堵影响，反映到当前时刻各个路径共享汽车的输入量上，从而影响当前时刻及以后时刻的道路拥堵，继续影响下一时刻用户需求。

2 优化模型

2.1 目标函数

用Z表示单向式共享电动汽车系统一天的总利润，目标函数如下：

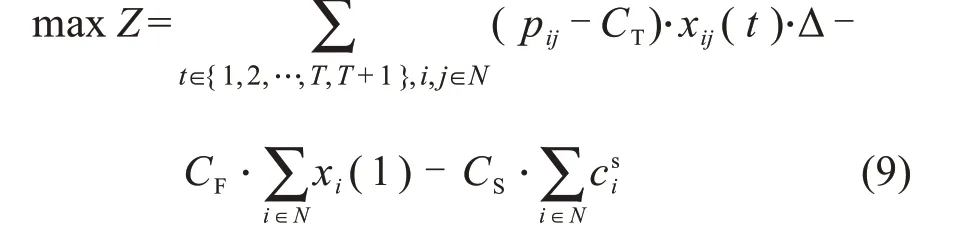
共享电动汽车系统的收入仅来源于用户，总成本包括车辆用电成本、车辆固定成本（包括摊销成本、折旧、保险和维护成本）和停车位成本。

2.2 约束函数

（1）拥堵约束。设置车站拥堵和路径拥堵两种拥堵约束，分别保障用户和公众利益，则：

3 优化算法

本文选取MADS 算法和遗传算法对模型进行求解。

3.1 MADS算法

MADS 算法隶属于直接搜索算法，在优化问题时，不需要提供目标函数的梯度或者高阶导数信息。它通过搜索当前点周围的一系列点（这些点组成一个小的单位称为“网格”），不断检查试验解集合，一旦发现试验解优于当前解则更新当前解，否则，形成新的“网格”，再检查试验解。具体算法如下所示：

输入：目标函数f(x)、约束条件Ω、初始点x0∈Ω、障碍函数fΩ(x)。

Step 1 初始化

设初始尺寸参数Δ0∈(0,∞)，正生成矩阵D=[In-In]，In为n维单位矩阵，正生成矩阵Dk，网格尺寸调整参数τ∈(0,1)，迭代精度εstop∈[0,∞)，迭代代数k←0。

3.2 遗传算法

遗传算法是一种通过模拟自然进化过程搜索最优解的启发式算法，其鲁棒性强、适用范围广泛，能够解决复杂系统优化问题。算法受到自然界生存原则“优胜劣汰”启发，从初始解开始，通过选择、交叉、变异得到新一代解。针对本文所提出的复杂MINLP 问题，我们选择遗传算法作为优化算法之一。

4 数值实验

通过运用实际数据对小规模共享电动汽车系统网络模型进行求解，小规模网络站点数选取为30个，站点分布如图1所示。原始数据为2014年4月11 日成都市出租车的全天行程数据，选择运营时间为6:00～24:00。通过对原始行程数据进行处理，选取站点位置，确定模型的输入参数(道路占有率、路径容量等)，主要进行以下两个实验：（1）在设置不同车站溢出率约束的场景下，对优化模型分别设计遗传算法和MADS 算法进行求解，比较两种算法的求解效果；（2）根据1.3 中出行需求与价格和拥堵的弹性关系模型，分别调整价格和拥堵参数求解模型，研究需求、价格、拥堵对共享电动汽车系统优化决策的影响。

图1 30个共享汽车服务车站站点位置图Fig.1 Location of 30 carsharing stations

根据成都市实际情况，系统定价和相关配置单位成本取值如表2所示。

表2 定价和相关成本取值表Tab.2 Pricing and related costs

4.1 MADS算法和遗传算法求解效果分析

为了设置两种算法的最优参数值，首先对MADS 算法和遗传算法分别设置不同的参数求解模型，得到结果如表3、表4所示。

表3 不同参数设置下MADS算法的优化结果Tab.3 Optimization results of MADS algorithm for different parameter settings

表4 不同参数设置下遗传算法的优化结果Tab.4 Optimization results of GA algorithm for different parameter settings

遗传算法最大迭代代数均为6 000，使用并行计算，各组实验均在最大迭代代数参数内得到最优解。根据表3、表4 结果，两种算法参数值分别采用最优结果下的参数值，即：MADS 算法最大迭代代数为50 000，最大函数评估次数为500 000；遗传算法最大迭代代数为6 000，种群大小为100，最大稳定代数为500。

图2 为两种算法在无约束场景下的算法收敛图，MADS 算法在函数评估次数为5 000 左右时接近最优解，遗传算法在函数评估次数为100 000 左右时接近最优解，MADS 算法收敛速度更快。为了进一步比较两种算法，在模型其他参数不变的情况下，设置不同的车站溢出率约束场景分别进行求解，遗传算法在达到算法精度要求下均得到了收敛解，MADS 算法在达到最大迭代次数后得到了良好的可行解。两种算法在7 种场景下的CPU 运行时间和最大日利润如图3 所示。横轴车站溢出率最大值ω的取值范围设定为{0,0.2,0.4,0.6,0.8,1}，无车站溢出约束用ω=∞表示。遗传算法在不同场景下的CPU 运行时间均超过4 h，最长达到11.70 h，最短为4.38 h，平均CPU 运行时间为7.45 h；MADS 算法在所有场景下的运行时间均小于4 h，最快为2.21 h，最慢为3.12 h,平均运行时间为2.71 h。在同种场景下，MADS 算法的优化目标值均大于遗传算法优化目标值。结果表明，MADS 算法收敛更快，并在得到更优解的情况下计算时间均少于遗传算法，即在解决本模型上，MADS 算法在收敛速度、计算效率和结果上更具优势。

图2 MADS算法和遗传算法收敛图Fig.2 Convergence diagrams of MADS algorithm and GA

图3 不同车站溢出约束场景下MADS算法和遗传算法优化最大日利润和CPU运行时间对比图Fig.3 Comparison of maximum daily profits and CPU operating time of MADS algorithm and GA under different station overflow constraints

4.2 拥堵与需求的交互影响

为了研究需求和拥堵的交互影响对系统的影响，我们首先不考虑交互影响，假设用户实际出行需求dij(t)只与系统定价pij相关，求得各道路拥堵场景的优化结果如表5 所示。其中，F表示车队规模，S表示停车泊位数，再将优化结果带入考虑交互影响的模型中，得到对比结果如图4所示。横轴“道路拥堵系数”为模型输入道路占有率ηij(t)与基准道路占有率的比值，其中，基准道路占有率为出租车行程数据处理所得，当道路拥堵系数等于2时，模型输入道路占有率ηij(t)等于2 倍基准道路占有率。图4（b）纵轴“系统服务率”为一天服务行程数与用户实际出行需求的比值，图4（c）纵轴“车辆利用率”为平均每辆车一天行驶时间与运营时间的比值。结果表明，不考虑交互影响的最大日利润、系统服务率和车辆利用率均低于考虑交互影响的情况；考虑交互影响后，由于共享汽车的引入导致道路占有率增加，反馈给用户需求，实际出行需求dij(t)与潜在出行需求Dij(t)均产生差异，服务行程数减少，在中等拥堵程度（道路拥堵系数=1.5）时，不考虑交互影响而高估的出行需求数最大，接近1 800个。

图4 考虑需求和拥堵交互影响后的系统性能变化Fig.4 System performance changes after considering the interaction effects between demand and congestion

表5 不考虑交互影响的共享电动汽车系统配置优化结果Tab.5 Optimization results of carsharing configuration without considering interaction effects

4.3 敏感度分析

在模型其他参数不变的情况下，设置不同的需求场景对模型进行优化。表6 为不同需求场景下的优化结果。第一列“需求场景”的数值为模型潜在出行需求输入值Dij(t)与基准潜在出行需求的比值，其中，基准潜在出行需求为出租车行程数据处理所得，当需求场景等于2时，模型潜在出行需求输入值Dij(t)等于2倍基准潜在出行需求。结果显示，车站停车泊位数与车队规模比值的均值为2.11，最大达到2.71，这是因为系统的动态随机环境可能会造成某个车站某时刻车辆存积过多的现象，需要配置较大的停车泊位数来满足一定的用户还车服务率，即在不考虑调度的情况下，车站停车泊位数与车队规模的比值处于1.8～2.7 左右时，系统能够达到最好的收益效果，并解决由供需不平衡所产生的车站溢出严重的情况，在不同需求场景下全天总车辆溢出数最大也仅为4辆。

表6 不同需求场景下的优化结果Tab.6 Optimization results for different demand scenarios

为了研究道路拥堵和定价对共享电动汽车系统优化决策的影响，分别设置不同的道路拥堵场景和定价场景，对模型进行求解，得到优化结果如图5 所示。值得注意的是，在定价影响实验时，我们设置了较大的价格弹性系数，使得当定价超过5 元/min 时，实际出行需求dij(t)趋近于0。

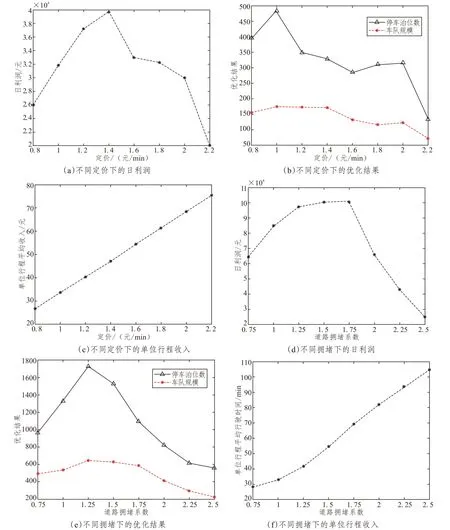
图5 不同道路拥堵和定价场景下的优化结果Fig.5 Optimization results for different road congestion and pricing scenarios

结果表明，由于价格的增高，系统服务行程减少，但单位行程平均收入增加，在定价为1.4元/min时，系统达到最大利润；随着道路占有率的增加，系统流失的潜在出行需求越多，但平均单次出行时间越长，当道路处于中度拥堵（全网平均道路占有率处于0.68～0.80）时，运营商能够获得可观的日利润，最大日利润出现在道路拥堵系数=1.5（全网平均道路占有率为0.77）时。

5 结束语

本文在动态随机环境下，基于流体排队理论，考虑用户出行需求和道路拥堵的交互影响，构建了以运营商日利润最大化为目标的MINLP 模型，模型可以同时兼顾运营商、用户、公众三方利益。为了解决本文所构建的MINLP 问题，分别设计MADS 算法和遗传算法对系统决策进行优化求解。分析对比两种算法，并针对30 个车站的网络进行了多组实验，得到的结论如下：

（1）在解决本文MINLP模型时，MADS算法收敛速度、求解效率和结果均优于遗传算法。在解决同一组实验时，MADS 算法平均计算时间为2.71 h，遗传算法平均计算时间为7.45 h，接近MADS算法的3倍，且其最大日利润均小于MADS求解的最大日利润。

（2）在不考虑调度的情况下，车站停车泊位数与车队规模比值在1.8～2.7 之间时，能够有效满足较小的车站溢出约束取得最大利润，并解决由供需不平衡所产生的车站溢出严重的情况。在不同需求场景下，全天最大车站溢出率均仅为0.1左右。

（3）忽略需求和道路拥堵交互影响的系统将全面降低运营商利润、系统服务率和车辆利用率。由于共享汽车的引入势必吸引大量公交乘客，引起道路拥堵的增加，从而影响用户出行需求，忽略这种交互影响将过高估计用户需求。

（4）适当的道路拥堵能够增加运营商利润，实验证明，当道路处于中度拥堵（全网平均道路占有率处于0.68～0.80）时，考虑交互影响的共享电动汽车系统能够达到最大利润，而忽略交互影响的共享电动汽车系统将最大化地过高估计用户出行需求，在全网平均道路占有率为0.77 时，被高估的用户出行需求接近1 800个。

（5）过高或过低的定价都将减少运营商利润，当定价等于1.4元/min时利润达到最大。

本文构建了共享电动汽车流体排队模型，联合优化动态随机环境下的共享电动汽车系统车队规模和停车泊位数，讨论了需求、拥堵、定价对优化结果的影响，相关研究成果可为共享电动汽车系统配置层面决策提供理论基础。共享汽车系统优化涉及规划、配置、运营三个层面的决策，文中仅以配置层面决策为优化变量，实际运营层面并未考虑，因此，后续研究将考虑配置层面（车队规模和停车泊位数）与运营层面（动态定价、车辆调度）的联合优化，从中长期决策和日常运营决策两方面出发，为共享电动汽车系统提供更有效的理论支持。