基于Cosserat连续体理论的微纳米螺旋结构轴向负载力做功研究

顾正法，尤 嘉，戴 璐

（苏州科技大学 物理科学与技术学院，江苏 苏州 215009）

三维螺旋结构普遍存在于自然、科学、艺术以及建筑学中，而微纳米尺寸螺旋结构的应用遍布于当今科学的各个领域，如电子学、光电子学、微纳米电子机械系统、传动传感系统等[1-4]。实验发现某些微纳米螺旋在高负载的作用下产生较大的轴向形变，当撤去负载时，螺旋恢复原形，这一性质体现出螺旋具有优秀的弹性性质[5-10]。微纳螺旋的超弹性使得其在介观／量子器件及其集成上具有更巨大应用潜力，特别是在传动器、振荡器、发动机、缓冲装置、磁场探测器、化学生物传感器、弹性能储存器件以及电磁波吸收装置等能获益于弹性性能的领域，比如具有超大带宽的微波纳米天线，可以提供超高共振频率[11]。

笔者基于Cosserat连续体理论，建立模型并定量研究了在螺旋拉伸端不可自由旋转和可以自由旋转两种条件下，圆形横截面螺旋、矩形横截面法线螺旋和矩形横截面副法线三种螺旋结构的轴向负载力做功问题。研究结果表明，拉伸端不可自由旋转的条件下，相同应变时，矩形横截面法线螺旋负载力做功值最大。

1 圆截面螺旋结构

1.1 模型

基于Cosserat连续体理论，笔者建立了圆形横截面螺旋模型来研究碳纳米管螺旋结构在轴向负载拉伸时的负载力做功问题（如图1所示）。由图1（a）可见，假设一圆形横截面螺旋HCI，半径a0，螺距b0，匝数N0，圆截面半径r，螺旋方向基矢Di（i=1，2，3）。由图1（b）可见，若螺旋拉伸端不能旋转，在轴向拉伸力F作用下，螺旋HCI形变为螺旋HCF1，半径a，螺距b，匝数N0，螺旋方向基矢di（i=1，2，3）。由图1（c）可见，若螺旋拉伸端可以旋转，在轴向拉伸力F作用下，螺旋HCI形变为螺旋HCF2，半径a，螺距b，匝数N。由于螺旋一端可以自由旋转，所以在负载过程中螺旋的匝数会发生变化。

图1 拉伸端不可旋转和可旋转圆形横截面螺旋结构受到轴向拉伸力作用后发生形变

在之前的研究中，笔者发现圆形横截面螺旋具有旋转反转特性，即在轴向拉伸过程中，螺旋自由端先过卷再退卷，螺旋匝数先增大后减少[12]。方向基矢Di和di分别由两组欧拉角φ0，θ0，ψ0和φ，θ，ψ定义[13，15]。根据Cosserat模型中圆截面螺旋结构的推导过程[16]，对于螺旋拉伸端不能旋转的情况，考虑到拉伸过程中螺旋的匝数不变，可以写出形变前螺旋的半径、螺距的表达式为

轴向形变后，螺旋半径、螺距的表达式为

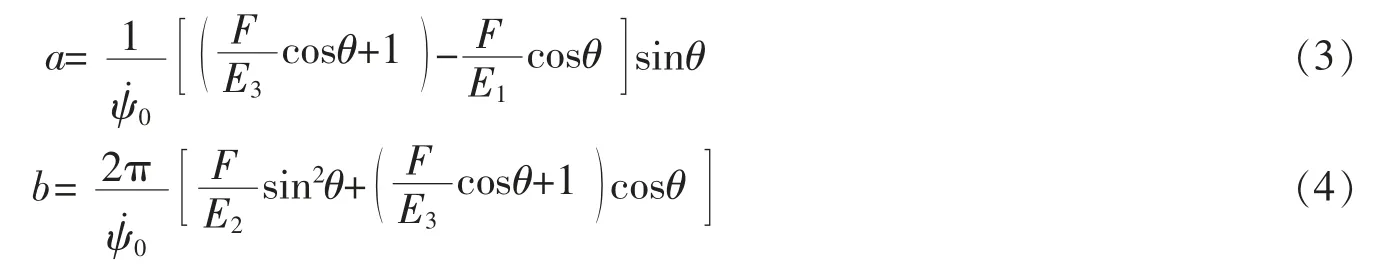
以及轴向负载力F满足的平衡方程

对于拉伸端可以旋转的情况，考虑到螺旋轴向力矩为零，形变前半径、螺距的表达式与方程（1）和（2）相同。推导得到螺旋的半径、螺距的表达式为

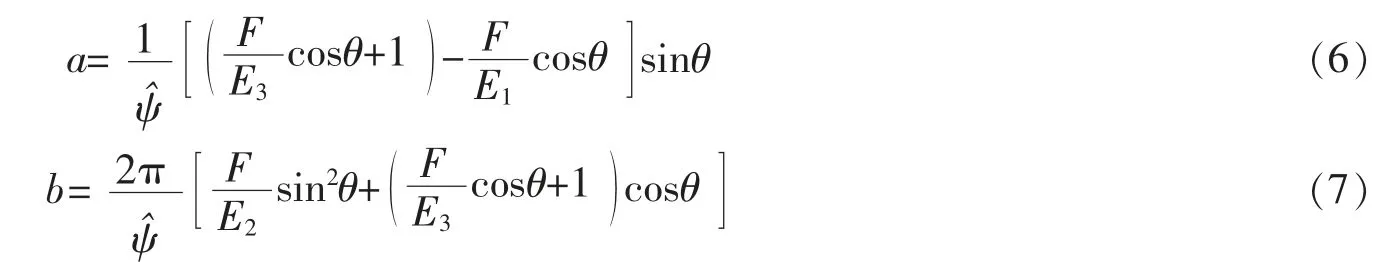
以及轴向负载力F满足的平衡方程

其中

其中E2=KGπr2，E3=Eπr2，B=EI以及C=GJ。K为TimosHenko剪切系数[14]，可用泊松比ν来表示

E和G=E/2（1+ν）分别是杨氏模量和切模量[17-18]。圆截面的I=（πr4）/4和J=（πr4）/2分别是截面的转动惯量和极转动惯量。计算负载力做功，忽略细杆的拉伸和剪切形变，即基尔霍夫模型的情况。根据方程（4）和（7），此时拉伸端不可旋转和拉伸端可旋转的螺距表达式分别简化为

同样，忽略细杆的拉伸和剪切应变之后，结合方程（5）和（8），此时拉伸端不可旋转和拉伸端可旋转的轴向负载力F满足的平衡方程可以简化为

对拉伸端不可旋转的情况，根据方程（10）和（12），以及功的定义W=∫Fdx得到轴向负载力F做的功为

对拉伸端可旋转的情况，根据方程（9）、（11）和（13），以及功的定义得到轴向负载力F做的功为

1.2 结果与讨论

利用碳纳米管螺旋负载实验结果来定量研究轴向负载力拉伸圆截面螺旋被轴向拉伸时的做功问题。参数如下：a0=1.18 μm，b0=4.47 μm，r=226 nm，N0=6，ν=0.32[10]。因为实验中的螺旋结构是由碳纳米管和聚氨酯组成的复合材料，为了得到其精确的杨氏模量值，利用方程（2）-（5）和文献[10]中图2（d）负载力随应变变化的曲线，在900%应变范围内，计算得到杨氏模量的平均值为E=2.5 GPa。如图2（a）所示，分别结合方程（2）、（4）、（5）和方程（2）、（7）、（8）、（9），以及以上几何参数和材料参数，计算得到了在螺旋拉伸端不可旋转的条件下HCF1（实线）和在螺旋拉伸端可旋转的条件下HCF2（点线）的轴向负载力随轴向应变的变化关系。在螺旋拉伸量为原长的0～500%时，两种结构在同应变情况下轴向拉伸力几乎相同，轴向负载力的变化范围是0～0.3 N。当拉伸量为原长的500%～800%时，对于相同的轴向应变量，螺旋HCF1的负载拉伸力比螺旋HCF2的大。在应变达到800%时，螺旋HCF1的轴向拉伸力为1.35 N，螺旋HCF2的拉伸力为1.15 N。

图2 拉伸端不可旋转和可旋转圆形横截面螺旋结构的轴向负载力和做功随应变的变化

如图2（b）所示，分别根据方程（2）、（4）、（14）和方程（2）、（7）、（9）、（15），及以上几何参数和材料参数，计算得到了螺旋HCF1（实线）和螺旋HCF2（点线）的轴向负载力做功随轴向应变的变化关系。两条曲线几乎重合，在拉伸到原长的800%时，螺旋HCF1的负载力做功为4.80 mJ，螺旋HCF2的负载力做功为4.82 mJ，两者仅相差螺旋HCF1值的0.4%。

2 矩形截面螺旋结构

2.1 结构模型

利用Cosserat理论，除了研究圆形横截面螺旋结构的做功问题，还能研究矩形横截面螺旋结构的做功问题。如图3（a）所示，假设一法线矩形横截面螺旋HNI[19]，半径a0，螺距b0，匝数N0，矩形横截面长w、宽t（w>t），螺旋方向基矢Di（i=1，2，3）。如图3（b）所示，若螺旋拉伸端不可旋转，在轴向拉伸力F作用下，螺旋HNI形变为螺旋HNF1，半径a，螺距b，匝数N0，螺旋方向基矢di（i=1，2，3）。如图3（c）所示，若拉伸端可以旋转，在轴向拉伸力F作用下，螺旋HNI形变为螺旋HNF2，半径a，螺距b，匝数N。图3（d）-3（f）分别表示的是：形变前的副法线矩形横截面螺旋HBI[20]；螺旋拉伸端不可旋转时，轴向拉伸形变后的螺旋HBF1；螺旋拉伸端可以旋转时，轴向拉伸形变后的螺旋HBF2。

笔者之前的研究表明，在轴向形变过程中，法线螺旋会发生过卷（即螺旋匝数增加），而副法线螺旋会发生退卷 （即螺旋匝数减少）[12]。根据Cosserat模型中矩形截面螺旋结构的 推 导 过 程[12，21]，形 变 前 后 螺旋的半径、螺距的表达式分别和方程（1）－（4）形式相同。

轴向拉力F满足的平衡方程

图3 拉伸端不可旋转和可旋转矩形横截面螺旋结构受到轴向拉伸力作用后发生形变

在以上方程中，对于拉伸端不可旋转的情况，根据拉伸过程中螺旋匝数不变，可得

对于拉伸端可旋转的情况，根据螺旋轴向力矩为零，可得

其中Δ=I2/I1，i=1（i=2）对应的是矩形的法线螺旋（副法线螺旋）结构，δi2是Kronecker常数，E1=E2=KGwt，E3=Etw，B=EIi并且C=4GI1I2/（I1+I2）[22]，I1=w3t/12，I2=wt3/12，K=（5+5v）/（6+5v）[23]，E和G（G=E/2（1+v））分别是材料的杨氏模量和切模量。

同样，计算负载力做功时，忽略细杆的拉伸和剪切形变，即基尔霍夫模型的情况。此时拉伸端不可旋转和拉伸端可旋转的螺距表达式分别与方程（10）-（13）相同。

对拉伸端不可旋转的情况，根据方程（10）、（11）、（16）和（17），以及功的定义W=∫Fdx得到轴向负载力F做的功为

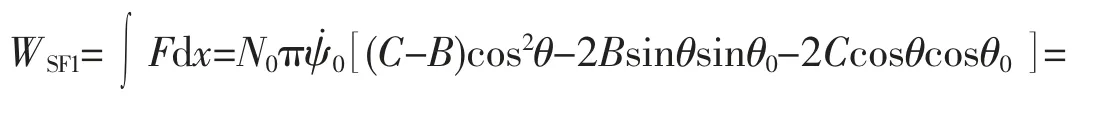
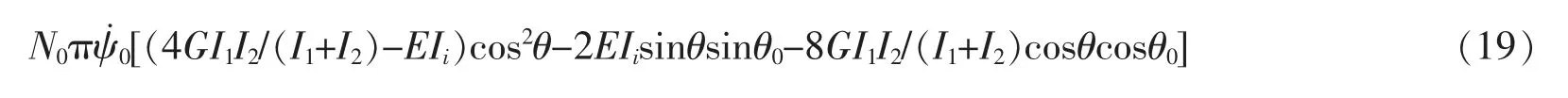
对拉伸端可旋转的情况，根据方程（12）、（13）、（16）和（18），以及功的定义得到轴向负载力F做的功为

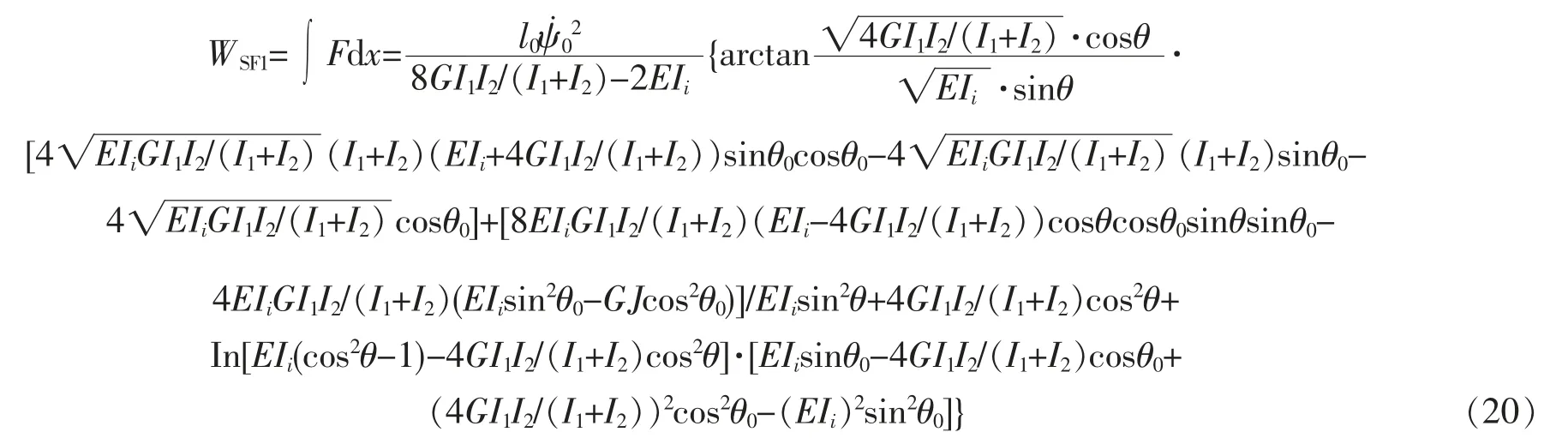
其中i=1（i=2）对应的是矩形的法线螺旋（副法线螺旋）结构。

2.2 结果与讨论

利用SiGe/Si/Cr微米螺旋带的材料参数[12]来定量研究轴向负载力拉伸矩形截面螺旋被轴向拉伸时的做功问题。参数如下：a0=1.18 μm，b0=4.47 μm，t=1.57 μm，w=31 nm，N0=6，E=2.5 GPa，ν=0.31。首先，笔者研究了法线螺旋的情况，如图4所示。

图4 拉伸端不可旋转和可旋转矩形横截面螺旋结构的轴向负载力和做功随应变的变化

如图4（a）所示，分别结合方程（2）、（4）、（16）、（17）和方程（2）、（4）、（16）、（18）（公式中取i=1），及以上几何参数和材料参数，计算得到了矩形横截面法线螺旋在拉伸端不可旋转的条件下HNF1（实线）和拉伸端可旋转的条件下HNF2（点线）的轴向负载力随轴向应变的变化关系。螺旋轴向应变随负载力的增加而增大，对于相同应变，螺旋HNF1比螺旋HNF2的负载力更大。在螺旋拉伸量为原长的80%时，螺旋HNF1轴向拉伸力为70 mN，螺旋HNF2轴向拉伸力为20 mN。如图4（b）所示，笔者分别结合方程（2）、（4）、（19）和方程（2）、（4）、（20）（公式中i=1），及以上的几何参数和材料参数，计算得到了矩形横截面法线螺旋在拉伸端不可旋转的条件下HNF1（实线）和可旋转的条件下HNF2（点线）的轴向负载力做功随轴向应变的变化关系。螺旋HNF1对应的做功值随着应变增加而显著增大，当应变为原长的80%时，其轴向力做功为3.2 nJ。而螺旋HNF2对应的做功值随着应变增加几乎不变，当应变为原长的80%时，其轴向力做功仅为0.3 nJ，是螺旋HNF1的轴向力做功值的1/10。其次，研究了副法线螺旋的情况，如图4（c）所示分别结合方程（2）、（4）、（16）、（17）和方程（2）、（4）、（16）、（18）（公式中取i=2），及以上的几何参数和材料参数，计算得到了矩形横截面副法线螺旋在拉伸端不可旋转的条件下HBF1（实线）和可旋转的条件下HBF2（点线）的轴向负载力做功随轴向应变的变化关系。螺旋轴向应变随负载力的增加而增大，对于相同应变，螺旋HBF1比螺旋HBF2的负载力更大。在螺旋拉伸量为原长的80%时，螺旋HBF1轴向拉伸力为1 μN，螺旋HBF2轴向拉伸力为0.6 μN。如图4（d）所示，分别结合方程（2）、（4）、（19）和方程（2）、（4）、（20）（公式中i=2），及以上的几何参数和材料参数，计算得到了矩形横截面副法线螺旋在拉伸端不可旋转的条件下HBF1（实线）和可旋转的条件下HBF2（点线）的轴向负载力做功随轴向应变的变化关系。功随着应变增加而增大，对于相同的应变，拉伸端不可旋转的副法线螺旋HBF1比可以旋转的副法线螺旋HBF2的做功值更大。但是，同法线螺旋的情况相比，这种差别要小的多。当应变为原长的80%时，螺旋HBF1的轴向力做功为6.5 pJ，螺旋HBF2的轴向力做功为5 pJ，两者相差螺旋HBF1值的23%。所以，无论是法线螺旋还是副法线螺旋，都是拉伸端不可旋转的条件下，相同应变对应的做功值更大，机械性质更好。

3 拉伸端不可旋转的条件下，三种结构的做功对比

根据第2节讨论结果，拉伸端不可旋转的螺旋，机械性质更好。如图5所示，笔者对比了拉伸端不可旋转的条件下，圆形横截面螺旋HCF1（点划线）、矩形横截面法线螺旋HNF1（实线）和矩形横截面副法线螺旋HBF1（点线）的轴向负载力做功值随轴向应变的变化关系。用到的公式分别为（2）、（4）、（14）和方程（2）、（4）、（19）（i=1对应法线螺旋HNF1；i=2对应副法线螺旋HBF1）。

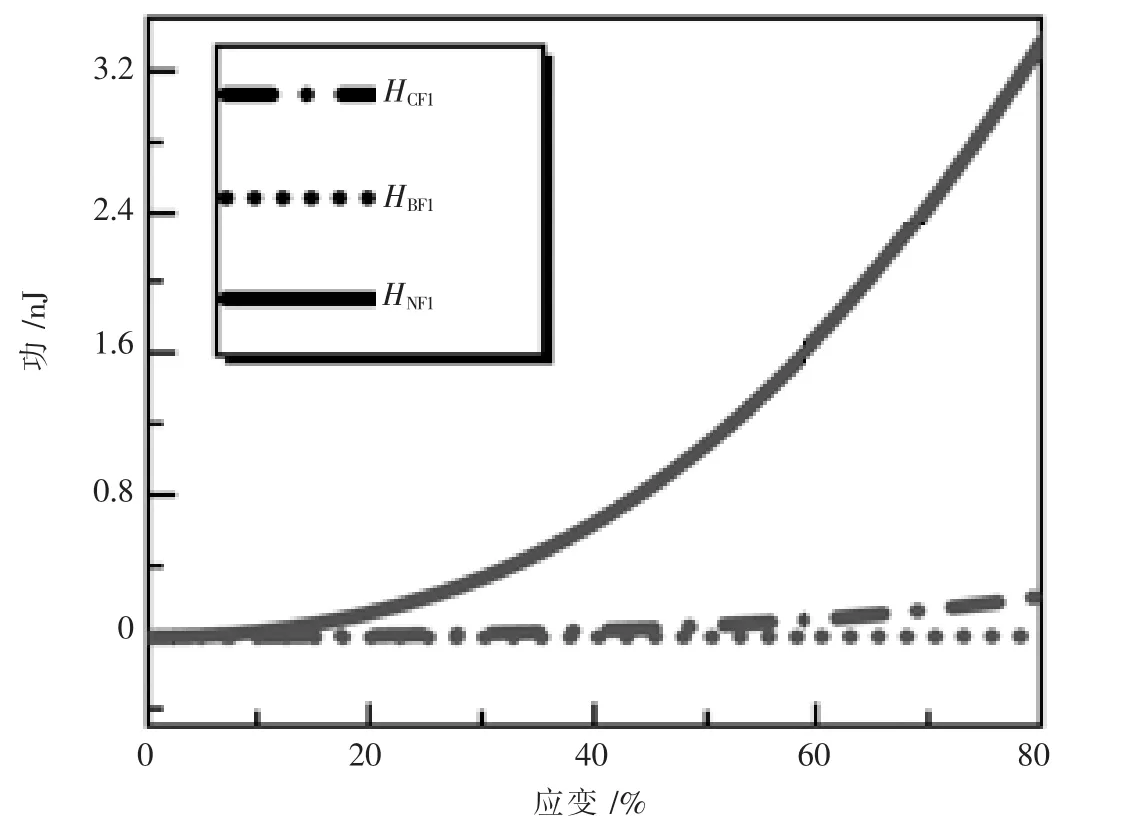
图5 拉伸端不可旋转的圆形横截面螺旋结构和矩形横截面螺旋结构的轴向负载力做功随应变的变化

这里，为了有效对比三种结构，笔者计算圆形横截面螺旋HCF1时，除了横截面半径r之外，用了碳纳米管和聚氨酯的复合材料的几何参数和材料参数，即与矩形横截面螺旋的面积相同。对于横截面半径r，笔者假设圆形横截面面积和实验材料的横截面面积相同，由此计算得到半径r=124 nm。对于在应变区间0～11%，三种结构在相同应变时的轴向拉伸力做功值几乎相同，做功的变化范围是0～0.1 pJ。在应变区间11%～80%，对于相同应变，螺旋HNF1的负载力做功值明显比螺旋HCF1和螺旋HBF1的大很多。在应变值80%时，这三种结构对应的做功值分别为3.2 nJ、0.27 nJ和5 pJ。矩形横截面法线螺旋HNF1的做功值是矩形横截面副法向螺旋HBF1做功值的640倍，是圆形横截面螺旋HCF1做功值的11.8倍。所以，三种结构中，螺旋HNF1机械性能最好。

4 结语

笔者基于Cosserat连续体理论，建立模型并定量研究了圆形横截面螺旋、矩形横截面法线螺旋和矩形横截面副法线三种螺旋结构的机械性质。推导得到螺旋拉伸端不可自由旋转和可以自由旋转两种条件下，三种螺旋结构做功的表达式。利用碳纳米管螺旋材料和聚氨酯的复合材料材料的几何参数和材料参数，计算对比了三种螺旋结构在两种条件下轴向负载力总功的情况。计算结果表明，对于圆形横截面螺旋结构，在大负载范围内，即螺旋几乎被拉伸为直线情况下，拉伸端是否可以自由旋转，对负载力做功值几乎没有影响。对于矩形横截面螺旋结构，在几乎所有拉伸范围内，相同应变时，拉伸端不可自由旋转的条件下，负载力做功值更大。进而对比了拉伸端不可自由旋转的条件下三种螺旋结构的轴向负载力做功值。结果表明，矩形横截面法线螺旋在相同应变时，负载力做功值最大，在应变值80%时，是矩形横截面副法向螺旋做功值的640倍，是圆形横截面螺旋做功值的11.8倍。所以，三种结构中，矩形横截面法线螺旋的机械性能最好。该文为将螺旋结构更好地应用于微纳米电子机械系统提供了理论框架。