几何直观素养培育的基本路径——以“勾股定理”数学实验教学为例*

孙朝仁 张 静

(江苏省苏州市高新区实验初级中学 215000) (江苏省苏州市教育科学研究院 215004)

《义务教育数学课程标准(2022年版)》将“几何直观”作为初中学段核心素养的主要表现之一，并明确其内涵为“运用图表描述和分析问题的意识和习惯．”具体分为4个层次：一是能够感知各种几何图形及其组成元素，依据图形的特征进行分类；二是根据语言描述画出相应的图形，分析图形的性质；三是建立形与数的联系，构建数学问题的直观模型；四是利用图表分析实际情境和数学问题，探索解决问题的思路．几何直观的作用就在于“把握问题的本质，明晰思维的路径”，不止于把复杂的数学问题变得简明、形象，更在于通过思维交往，探索解决问题的思路，预测结果．

本文主要以“勾股定理”实验教学为思维交往执行载体，通过识图抽象、画图建模,以及算图推理等思维交往方式，在“直观懂”的组织运演过程中，产生新思路、新方案和新方法，促进学生核心素养的长足发展．

1 识图抽象：几何直观素养培养的先行组织

识图抽象就是在直观观察的基础上，通过对事物共同属性的概括，剔除概念的非本质属性，抽象出概念本质特征的一种认知行为倾向．心理学认为，直观是从感觉的具体对象背后，发现抽象的、理想的能力．就这一认识来说，识图抽象的前提是呈现先行组织材料，识图抽象的过程是直观到具体，识图抽象的结果是抽象与表征．换句话说，识图抽象本身就是一种几何直观，是一种先行组织行为，是直观引起的行为潜能的持久的心理变化．

苏科版初中数学教材设置的“章头图”，一方面突出了概念的直观，另一方面凸显具体概念的本质特征．这有助于学生站在系统的高度认识数学，从直观过渡到抽象，建立概念表象，形成概念认知产生式．七年级数学第1章“数学与我们同行”的设置，旨在引领苏科版整套教材教学导向，让学生从生活到数学、从活动到思考、从具体到抽象、从图形直观到概念客观，形成概念产生式．因此，图形是从实物和模型第一次抽象后的产物，也是形象、直观的语言表征，是识图抽象的结果形态，是几何直观素养发展的先行组织行为．

一般情况下，抽象的理论概念“只有通过更为具体的解释这些概念的模型才能描述世界”．也就是抽象往往需要从具体开始，带有“特殊→一般→特殊”的思想意义．数学教育中的“问题情境”抑或“先行组织”都是数学抽象的思维基础，是概念形成的思维运行载体，是几何直观作用的结果．苏科版教材中的“数学实验室”“数学活动”“阅读”“读一读”“小结与思考”“课题学习”都是一种先行组织材料，起到几何直观的作用，促进学生对数学概念的理解与把握．当然，数学作为科学是不可以有情境的，但作为数学教育是可以有情境的．这能让学生从具体到抽象，从感性到理性，这就是一种几何直观素养．而识图抽象的意义就在于让学生更好地理解数学，让学生在直观的识图中，获得概念抽象的能力，从而发展几何直观、用好先行组织材料．为此，在识图抽象层面需要做好三个方面的工作：一是确立适合的学习目标，为识图提供具体指向；二是在识图的过程中进行自然的数学抽象，形成事实概念；三是用好先行组织材料，让学生在“模型→图形→文字→符号”这个抽象的过程中，建立客观概念．

不妨以“勾股定理”的概念发生为实验载体，从“跳一跳，够得到”的学习目标出发，说明识图抽象的微言大义，突出几何直观的跃迁作用，强调用好“先行组织材料”的指导意义，落实核心素养发展的根本任务．具体识图抽象过程如下：

(1)学习目标的确立

目标1是在具体情境中，探索勾股定理，发展合情思想；目标2是在应用勾股定理求直角三角形的未知边长中，发展数形结合思想．这里的第一个目标的关键词是“探索”，第二个目标的关键词是“应用”，前者指向概念合情思想的建立，后者旨在建立数感、符号意识，以及形成初步的数形结合思想．无论探索还是应用，都是“具体→直观→画图”的先行组织行为，这为识图抽象提供思维交往的基础．

(2)欣赏与思考的设置

包括两个问题：问题1是数一数图案(图1)中3个正方形内小方格的个数，你有哪些发现？问题2是说说图案的文化内涵，简单画出图案蕴含的基本图形，并说明画法．问题1的设置，旨在让学生从“直观的数与算→三个正方形面积关系的初步建立→直角三角形三边关系的初步确立”，即“9个小正方形+16个小正方形=25个小正方形”，也就是“两个较小的正方形的面积和等于较大的正方形的面积”；问题2的设置，旨在让学生经历“模型→图形→概念”，即“模型”是1955年希腊发行的一枚邮票，以此纪念毕达哥拉斯对“勾股定理”证明这一文化内涵．画图方法是以直角三角形的三边为边，向外作正方形，构造基本图形 (图2)，这就完成了“模型到图形”的第一次识图抽象，为概念符号的建立，以及文字表征奠定了直观的先行组织行为，有效地落实了核心素养的发展目标．

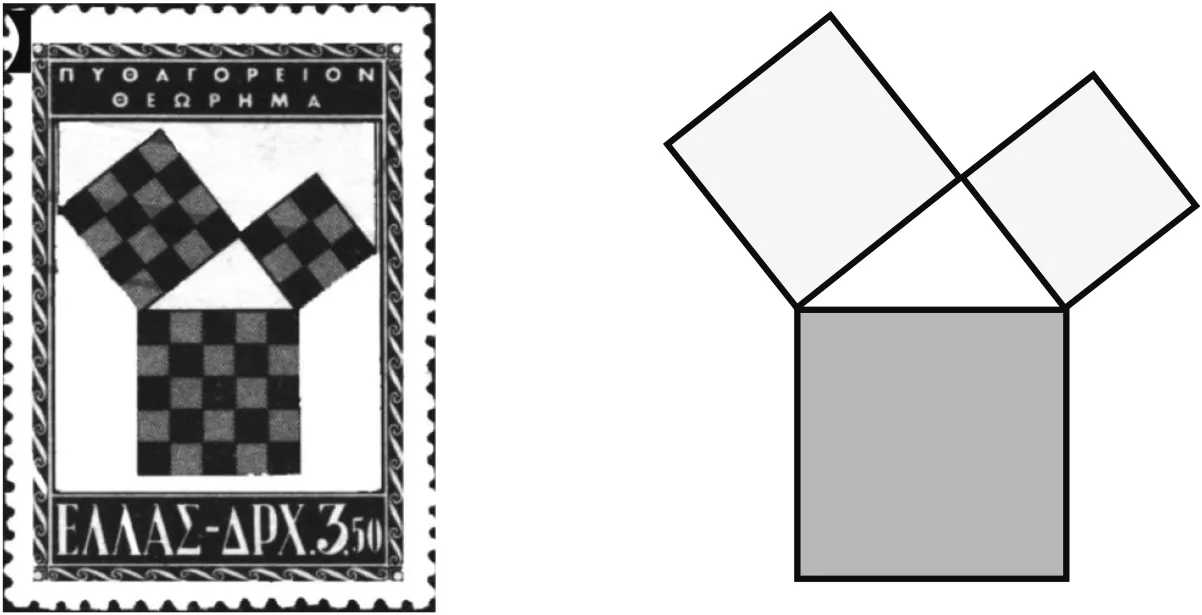
图1 图2

2 画图建模：几何直观素养培养的心理前提

画图建模是引起几何直观能力变化的持久性心理倾向，是培养初中阶段学生几何直观素养的思维途径．“画图→建模”的本质就是建立概念的心理原型，它起于“画图”，成于“建模”，终于“直观的懂”．实验教学过程中的“说一说”“做一做”“议一议”“试一试”都是画图建模的重要方式，是几何直观素养得以培养和缓存的心理前提．具体来说，我们通过画“线段的垂直平分线”，不止于“会画”，更在于通过“动手画”，建立概念原型，揭示“线段垂直平分线上的点，到这条线段的两个端点的距离相等”，促进线段是轴对称图形这一概念表象的建立；我们依据作法，画“角的平分线”，不止于画，不止于建立轴对称性，更在于揭示画法的合情依据(“边边边”或SSS)，从而使得画图、猜想、验证在实验教育学体系内，有了高度的统一性．这就是一种实验哲学，具体与抽象，或者画图与建模．在希尔伯特看来，了解一种理论的最好方法是找出然后研究那种理论的原型的具体例子．这里的“原型”可以理解为概念对象，而“具体例子”就相当于“举例说明”的直观作用．基于这样的认识，画角平分线、线段的垂直平分线，就是建立“轴对称图形”这一概念原型，形成概念产生式．

不难理解，几何直观是一种思维活动，是人脑对客观事物及其关系的一种直接识别或猜测的心理状态．画图本身就是一种几何直观，而“画图→建模”则是对象关系识别与建立的通用技术，有助于几何直观素养层级的提升与转化，是学生直观理解概念的思维抓手．《义务教育数学课程标准(2011年版)》在“课程内容”部分明确指出，在尺规作图中，了解作图的道理，保留作图痕迹，不要求写出作法．其中，“探讨作图道理+保留作图痕迹”的过程就是画图建模的实践形式，有助于建立识别和猜测，促进“直观懂”的从天而降，落实概念的有质量形成．教师应当努力开发制作简便实用的教具和学具，有条件的学校可以建立“数学实验室”供学生使用，这也在结论的背后，强调发展几何直观素养的重要性和方法指导．为此，在画图建模维度，需要做好三个方面的工作，方能提高几何直观素养培养的水平：一是任意画图，在辨别中形成直观概念心理；二是画一画，在直观猜想中建立概念属性；三是变式画图，促进概念本质特征的形成，形成“完形”概念产生式．

不妨以“勾股定理”的概念形成为实验载体，基于画图建模，突出几何直观素养培养的能力倾向，落实“直观懂”的意义．具体实验操作如下：

首先要求在方格纸上进行“画一画”活动．(1)任意画一个直角三角形，两条直角边的长分别为

a

,

b

，斜边为

c

，并以三边为边向外作正方形，其中两个小正方形的面积与大正方形面积之间有怎样的数量关系？写出结论并说明理由；(2)任意画一个锐角三角形，三边长分别为

a

,

b

,

c

，并以三边为边向外作正方形，其中两个小正方形面积与大正方形面积之间有怎样的数量关系？任意画一个钝角三角形呢？为什么？活动(1)旨在让学生从问题到建模，借助探讨正方形面积关系，形成勾股定理的初步概念；活动(2)旨在让学生通过补偿画图，产生概念辨别心理，直接对概念对象进行理解与把握．其中，任意画一个直角三角形是一种半开放问题，而任意画一个锐角三角形和一个钝角三角形，是一种变式画图，有助于学生在直观画中，形成猜想、形成辨别能力，突出直角三角形的三边关系，这就是画图建模的思维通道，有助于几何直观素养的自然积淀．接下来，教师呈现3个所画图形(图3)．其中，图3(1)旨在强调割补法对勾股定理概念形成的不可或缺性，是几何“三大语言”转换的思维现场(

a

+

b

=

c

)；图3(2)和图3(3)旨在让学生建立一般三角形的三边关系，即

a

+

b

>

c

或

a

+

b

<

c

．如果说任意画建立了语言概念，那么辨别画建立了特征概念，而“语言关系→图形关系→符号关系”的转换与建立，是勾股定理形成的标志，实现了画图建模的目标．

图3

3 算图推理：几何直观素养培养的运演条件

计算是一种逻辑推理，具有非完全演绎性，是直观思维得以过渡的运演条件，是学生学好数学推理的基础．算图推理顾名思义，就是让学生通过计算图形的面积，在几何思维的参与下，揭示概念对象的本质．在实验教学过程中，“拼图→算图→公式”“画图→算图→勾股定理”“打印纸→折纸→长与宽的比值的确立”“无盖立方体的制作→规律的发现”，等等都是算图推理的实验形式，有助于直观到抽象、直观到建模、直观到推理，形成“知其然，知其所以然”的直观背后的运演能力．事实上，就当前的初中教育现状来说，合格型数学教师依然是重视教知识，轻视教能力，课堂还是“一个概念+三项注意+复式练习”，“烧中段”现象极为普遍．就这一现象来说，课堂转型亟待解决，概念使用亟待规范，方能让学生在使用概念中形成概念能力，发展直观素养．算图推理是数学教育的一种“直观懂”的方式，是将感性认识上升为理性认识的一剂思维良药．在西方哲学家看来，直观就是未经充分的逻辑推理而对事物本质的一种直接洞察、直接把握对象的全貌和对本质的认识．这里的“洞察→把握→对象本质”是算图推理的重要环节，“洞察”在于几何直观，“把握”在于将感性上升为理性，“对象本质”在于关系性理解．正如斯根普指出的那样，只有从工具性理解(几何直观)达到关系性理解(算图推理)，学生才能把握数学对象的本质．

算图推理起于直观，终于逻辑，是逻辑推理的初级形式，有助于初中阶段学生直观地学好数学．在数学实验算理学范畴，逻辑推理是从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程．这里的“逻辑推理”是非完全演绎形式，属于算理逻辑的一种形式．“拼图→整式乘法+因式分解”“一提+二套+三分解”等都是算图推理的常见逻辑运演形式．这有助于学生“知其所以然”，建立概念关联．“逻辑规则”在数学实验领域被解释为实验步骤，就像“分式游戏”活动中的规则那样：每人制作几张卡片，在卡片上写一个简单的整式或运算符号；将其中的两张卡片分别放在分子、分母上，它们组成的式子是分式吗？如果是分式，它什么时候有意义？它的值能为0吗？这些“？”都是逻辑规则的外在表现形式，需要在直观支持下的算理解释，是对几何直观的有效反刍．为此，在算图推理过程中，需要做好三个方面的工作：一是变式训练，实现对概念的进一步把握；二是小结与思考，实现将课时概念上升为单元概念；三是概念关联，在进一步实验中，获得直观素养的关联发展．

不妨以“勾股定理”的概念使用为实验载体，运演算图推理的实践行为，落实直观素养的系统培养目标．具体实验过程如下：

首先呈现“使用概念”的算图推理的3个问题．(1)在图4中，当

x

=5，

y

=12时，

z

=

；当

x

=8，

z

=17时，

y

=

．(2)在图4中，如果两个小正方形的面积分别是81和144，则

z

=

．(3)如图5，直线

l

上有3个正方形

a

,

b

,

c

，若

a

,

c

的面积分别为5和11，则

b

的面积是多少？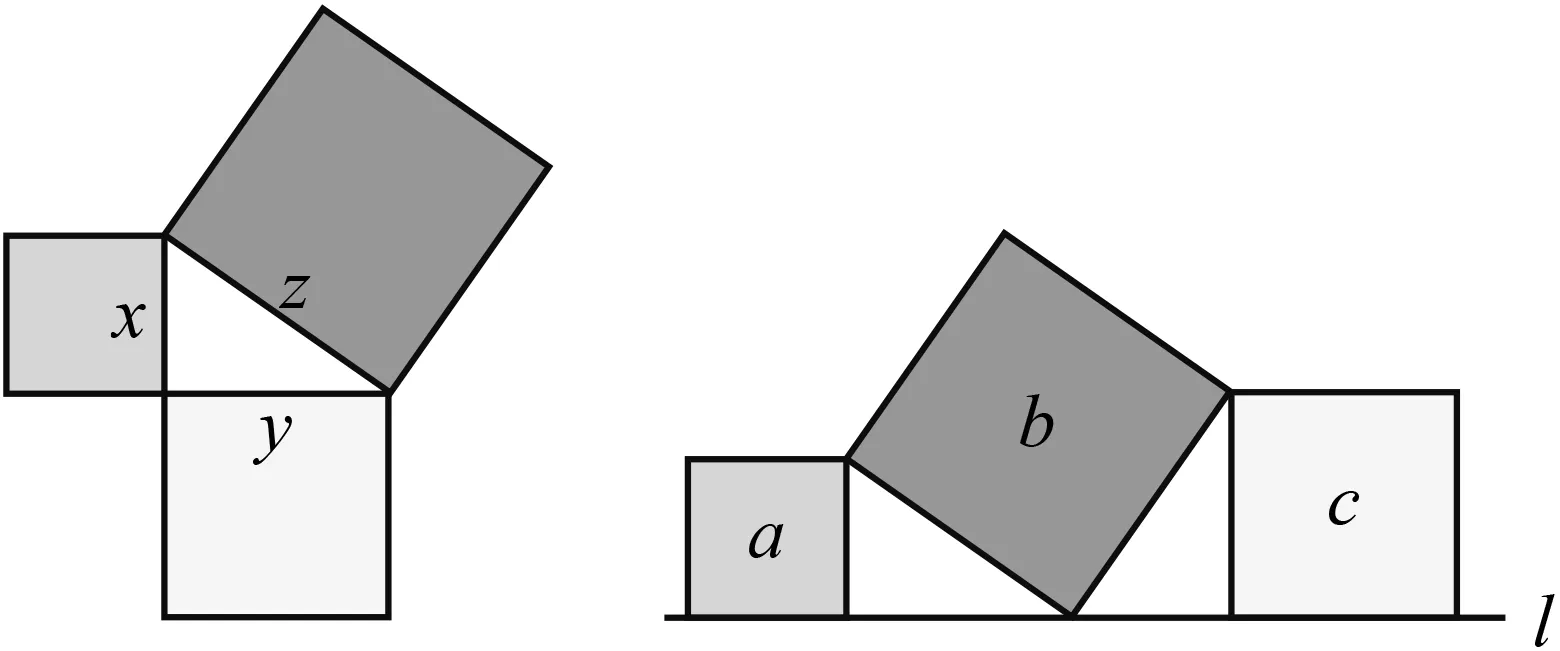

图4 图5

第(1)题是对勾股定理的工具性使用，第(2)题是回归概念，第(3)题是关系性理解，在全等 变换思维的参与下，落实算图推理，实现了将知识转化为能力．如果说，前两个问题是使用概念，则后一个问题是概念关联，有助于课时概念上升为单元概念，发展了学生的使用概念和运演概念能力．

图6 图7

接着，呈现“小结与思考”板块．(1)经历上述“画一画”活动，你得到了怎样的结论？(2)如图6，若每个小方块的面积都为1，画出图中以格点为端点且长度为5的线段；

(3)制作8张如图7的直角三角形纸片，分别拼成边长为

c

或(

a

+

b

)的正方形，你有何发现？

第(1)题是回归概念，突出勾股定理核心概念的再认知活动；第(2)题是对概念的变式使用，为后续“勾股定理逆定理”的学习铺设思维；第(3)题为勾股定理的验证提供活动经验，突破了传统数学实验的理解维度，立足于“系统概念”的建立，落实直观素养的培养功能．如果说“小结与思考”的第一个问题属于一种变式智慧，则后两个问题属于将课时概念上升为单元概念的新思想，很好地运演了算图推理．这种将系统概念的工具性理解上升为概念的关系性理解，能促进概念对象的把握，这才是数学实验未来课堂的样态．