云制造环境下机床资源租赁需求的优选方法
赵靖,陈建,阳复建,陶广福
(桂林航天工业学院管理学院,广西桂林 541004)
0 前言
自2010年李伯虎院士开创性地提出云制造以来,为实现制造资源的高度共享和有效配置,提高制造资源的使用效率和制造业的制造效率,国内外众多学者对云制造进行了深入研究。DELARAM和VALILAI提出云制造系统任务调度问题基本模型,以解决云制造系统中的操作共享和物流共享问题。HAYYOLALAM等对云制造环境下的服务组合和优化选择问题进行了系统研究。SONG等提出云制造环境中弹性增强服务组合与优化选择的HRGO方法。TONG和ZHU提出不确定偏好下基于对等效应的云制造服务匹配新方法。李珊珊等构建了中小门窗加工企业的云制造服务平台。贾海利等研究了云制造平台中资源需求的匹配策略。邓飞和冯运设计了以服务需求快捷响应为特征的云制造资源共享与管理模型。胡艳娟等对云制造环境下关于制造商选择的国内外研究现状进行了综述总结,并给出了未来的参考研究方向。机床设备是制造资源中的重要资源,也是推动制造业发展的重要力量,云制造环境下如何对机床资源进行优化配置的问题同样引起了学者们的广泛关注。姜兴宇等同时考虑质量、成本和资源利用率等因素,提出再制造机床资源的优化配对选择方法。龚小容等根据贝叶斯网络算法提出云制造环境下机床资源的选择方法。张富强等建立了云制造智能车间机床资源的再分配服务模型并进行了求解。王枭等人提出云环境中机床装备资源的服务建模方法。李孝斌对云环境下机床资源的特性进行了详细分析并提出其语义描述方法。李庆冬等提出基于本体的机床资源共享机制。周立新等以绿色制造为背景,对机床资源的选择方法进行了探讨。
以上文献均对云制造及机床资源进行了研究并取得了重要成果。总体看来,目前的研究主要侧重于机床资源需求方企业对提供方的考虑,即更多的是分析需求方如何优选提供方,而关于提供方对需求方进行选择的探讨却相对较少。另外,针对云环境下的机床设备制造资源,除了购买,租赁活动也时常在供需双方之间发生。一些生产制造企业因受制于自身经济水平,无力购买相对较为昂贵的机床设备,但由于制造的需要,具有机床资源租赁的需求。而另有一些制造企业,因为其机床设备生产能力过剩且预想获得更多收益,可提供机床资源租赁。由此,双方之间客观存在一种机床资源租赁共享活动。然而,优良的机床资源往往是租赁需求企业青睐的对象,那么资源提供方企业就会遇到同时面对多个需求方的租赁需求而需从中做出选择的情况。因此,研究该情形下提供方如何从需求方中做出选择具有重要意义,而目前尚未查到相关文献确切地提出机床资源租赁提供方选择需求方的方法。基于此,本文作者从提供方企业的视角,建立租赁需求方企业的评价指标体系,结合需求方企业的需求信息,运用熵权法和五级标度赋值法,获得评价指标具有主客观意义的综合权重,并改进TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法,进而对需求方进行评价,以此作为提供方决策选择的依据。
1 评价指标体系的构建与问题的描述
1.1 评价指标体系的构建
云制造环境下,当机床资源租赁提供方企业对需求方企业进行选择时,需有相应合理的指标对需求方进行评价。通过查阅相关资料并整理,充分考虑提供方对需求方进行选择时的影响因素,结合机床资源租赁供需双方的特点,以QoS评价技术为依据,建立如图1所示的需求方评价指标体系。
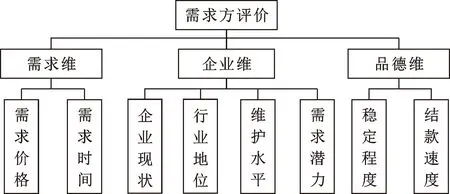
图1 需求方评价指标体系
(1)需求维。需求价格表示需求方企业对于其租赁需求愿意且能够为提供方支付的报酬;需求时间指需求方企业对机床设备资源的租赁时间间隔。两项指标可由需求方的需求资料信息中获得。

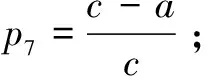
从提供方的角度考虑,各指标属性类型如表1所示。

表1 指标属性类型
其中,企业现状、需求潜力为语言变量,文中采用如表2所示的语言评价集。

表2 语言评价集
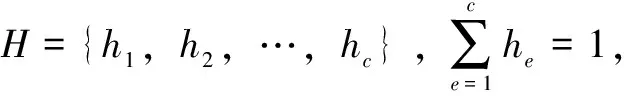



1.2 问题的描述
文中以上述8项指标对需求方进行评价,由评价指标体系,定义需求方企业的评价模型={,,,,,,,},设需求方企业集={,,…,},则需求方企业的评价指标属性集为

本文作者要解决的问题是提供方如何根据需求方评价指标属性集,科学地做出决策,选择最佳需求方。
2 机床资源租赁需求的选择模型与方法
2.1 评价指标客观权重的确定
熵权法是一种确定指标客观权重的有效方法。一般地,将评价对象集记为{}(=1,2,…,),指标属性集记为{}(=1,2,…,),评价对象的第项评价指标的指标属性值记为,则有如下指标属性集合:

然后根据以下步骤确定指标客观权重:
(1)评价指标的标准化处理。由于评价指标有正向型和负向型两种,需要对它进行标准化处理:
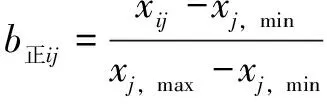
(1)
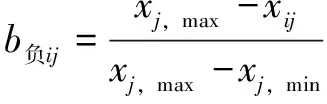
(2)
式中:,max、,min分别代表指标属性集中第列指标的最大值与最小值。正向型指标采用式(1)进行标准化,负向型指标采用式(2)进行标准化,标准化后得=()×。
(2)根据式(3)求解信息熵值
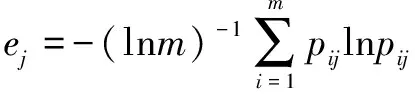
(3)
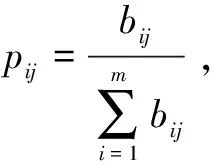
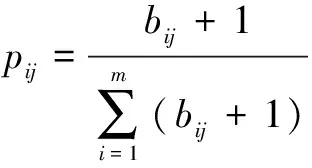
(4)
(3)根据式(5)计算各评价指标的变异程度系数
=1-
(5)
(4)由式(6)计算各评价指标的熵权,即客观权重

(6)
2.2 评价指标主观权重的确定
文中采用五级标度赋值法确定各指标主观权重,具体如下:
(1)评价指标赋值。设评价指标个数为,表示指标对的五级标度值,表3所示为五级标度赋值。

表3 五级标度赋值
对指标集进行赋值可得赋值矩阵:

(2)根据式(7)计算各指标的五级标度值之和

(7)
(3)由式(8)计算各指标的主观权重

(8)
2.3 评价指标综合权重的确定
记熵权法所确定的评价指标客观权重=(,,…,),记五级标度赋值法所确定的评价指标的主观权重=(,,…,),采用式(9)对评价指标的主客观权重进行综合,得评价指标的综合权重。
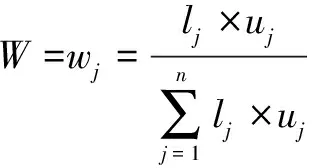
(9)
2.4 基于改进TOPSIS法的评价选择
由以上获得指标的综合权重后,可弥补TOPSIS法无法赋权的不足,有助于解决机床租赁提供方企业对需求方的选择问题。然而,传统的TOPSIS法存在一定局限:在指标数据获取过程中,易因指标之间的线性相关性而影响评价结果的科学性。对于该问题,李华等人试图引入马氏距离予以解决,但马氏距离的运用有评价指标个数不多于备选对象个数的前提条件,这一条件在很多决策问题中无法满足。鉴于此,文中引入向量夹角余弦,由相应数据信息构造空间中的特征向量,并通过计算两向量之间的夹角余弦度量其关联性,实现对TOPSIS方法的改进,以弥补传统欧氏距离与马氏距离的不足。
改进的TOPSIS法是一种逼近理想点的排序方法,其基本思路为:建立初始化决策矩阵,结合评价指标权重,将决策矩阵规范化处理并找出正、负理想点,再分别计算评价对象各评价指标与正、负理想点之间的向量夹角余弦距离,从而获得评价对象与理想点的相对贴近程度,并以此为依据进行选择。其中,向量夹角余弦是余弦定理在多维空间的推广,它利用数据信息构造空间中的特征向量,并通过计算两向量之间的夹角余弦度量其关联程度。具体为:把由原点指向评价对象各指标确定的空间点而构成的特征向量作为备选向量,记作,把由原点指向TOPSIS法所得的正、负理想点构成的特征向量看作理想向量,分别记作、。由此将传统TOPSIS法中计算评价对象同理想点的两空间点的最短距离变换为计算二者之间的余弦值,从而避免了线性相关问题,也解决了运用马氏距离的局限问题。
该方法在解决问题的过程中运用了代数思维向几何思维的转化,突破了单一维度思考问题的局限。此处以三维空间中备选向量同正理想向量之间的三维空间为例,如图2所示。

图2 向量夹角余弦距离

(1)构造初始矩阵。设备选方案个数为,评价指标个数为,文中取=8,以此构建如下初始矩阵

(2)为消除评价指标的不同量纲,需要对指标进行同趋势化处理,文中采用倒数法,即根据式(10)进行同趋势化处理:

(10)
得:

由于文中的评价指标大多为正向型指标,在进行同趋势化处理时,将负向型指标取倒数,使它与正向型指标同趋势。
(3)同趋势化后,根据式(11)进行规范化处理:

(11)
得:

(4)结合各评价指标的综合权重,根据式(12)得加权规范化矩阵
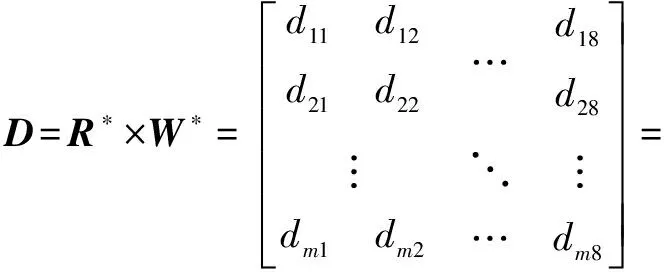

(12)
(5)确定最优、最劣理想方案
最优方案:

(13)
最劣方案:
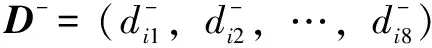
(14)
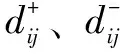
(6)根据下式计算评价对象到理想方案的向量夹角余弦距离
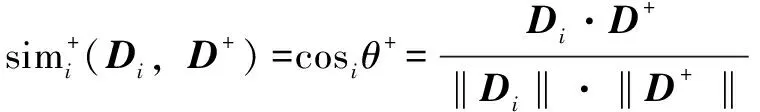
(15)
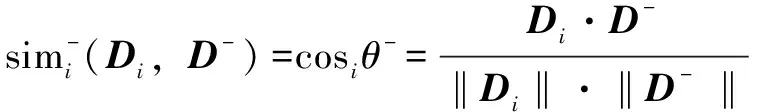
(16)
(7)计算贴近度并进行选择

(17)

3 算例
已知某制造企业H具有一流的、高质量、高性能的机床设备资源,在满足其自身生产需求外,还存在一定空余时期。H为充分发挥机床设备资源的效用,以获得更多利润,在云平台提供相应的机床租赁供给服务。设此时需求方企业A、B、C、D、E均有租赁H机床设备的强烈意愿。通过需求企业具体信息资料以及电话咨询、网络查找和相关领域专家评价等方式,得各需求方的需求信息如表4所示。现针对企业H如何从中选择最佳需求方,作以下分析并决策。
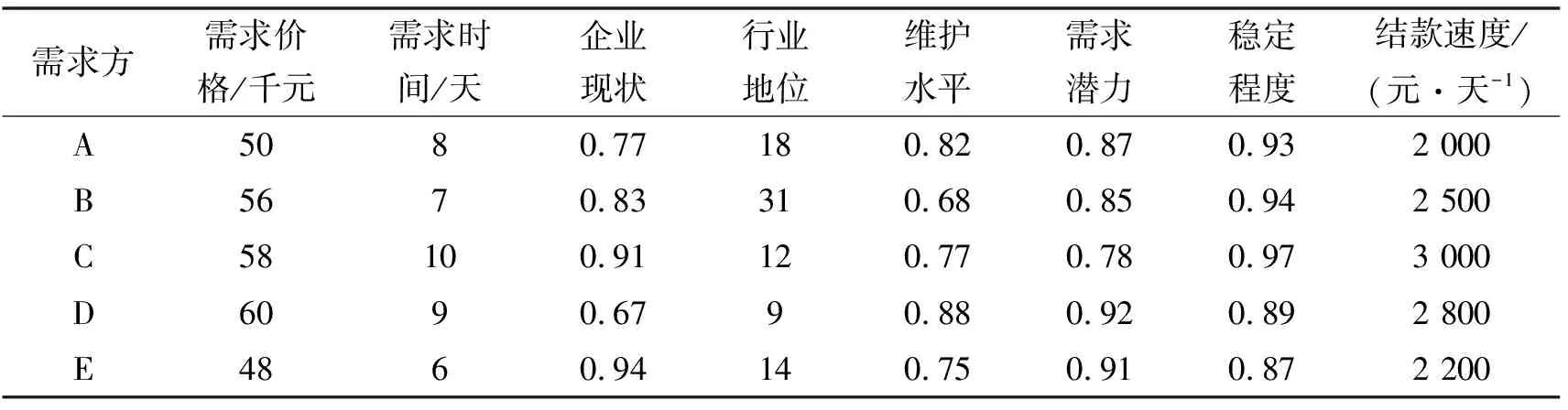
表4 需求方的需求信息
3.1 确定评价指标客观权重
由熵权法,根据式(1)—(6)求解各评价指标的客观权重向量=(0.146,0.126,0.123,0.110,0.113,0.116,0.129,0.137)。
3.2 确定评价指标主观权重
针对需求维、企业维、品德维3个维度,由提供方进行五级标度赋值,得如下矩阵:


3.3 确定评价指标综合权重
由式(9)得各指标的综合权重=(0.292,0.150,0.069,0.051,0.049,0.077,0.152,0.160)。
3.4 基于改进TOPSIS法的评价选择
由式(10)(11)将需求方企业的需求信息同趋势化处理和规范化处理得,结果如表5所示。

表5 同趋势化规范化处理后需求方的需求信息
结合各指标的综合权重,由式(12)得需求方需求信息加权规范化矩阵表如表6所示。

表6 需求方需求信息加权规范化矩阵
由式(13)(14)得最优、最劣理想解方案=(0.144,0.085,0.035,0.034,0.025,0.037,0.072,0.085),=(0.115,0.051,0.025,0.010,0.019,0.031,0.064,0.057)。由式(15)—(17)计算需求方到理想方案的贴近程度并排序,结果如表7所示。

表7 需求方评价最优、最劣距离及贴近度排序
根据表7可以得出,需求方企业E贴近度最大,即为最优需求方,企业H应该选择需求方E。
上述方法除了可以完成企业H对需求方企业的优选,还可以对各需求方企业进行较为详细的比较,分析未选中需求方的不足。根据加权规范化矩阵表相应数据,绘制各需求方指标属性折线图,如图3所示。

图3 各需求方评价指标数据对比
图3中,峰值越大代表越优,可以看出,需求方E在需求时间、企业现状指标方面明显优于其他需求方,另外6项评价指标虽不是最优,但与其他4家需求企业相较而言,也处于中等或偏上水平,因此最终需求方企业E被选中。而其他未选中的需求方可以根据该图找出自身的不足并加以改进,增强竞争能力。由此,将熵权法、五级标度赋值法同改进的TOPSIS法相结合的选择决策方法,不但可以使机床资源租赁提供方企业选择出最优需求方,还可以对需求方企业进行优劣分析,使需求方企业根据自身情况进一步完善。
4 总结
机床资源是云制造环境下重要的制造资源,租赁提供方企业如何从若干个需求方企业中进行选择是客观存在且需解决的问题。文中从提供方的视角,在对需求方企业精选决策时,考虑较为合理的评价指标,结合需求方的需求信息及提供方对指标的不同偏好,分别运用熵权法和五级标度赋值法计算出评价指标的客观权重和主观权重,并以此为依据得出评价指标的综合权重,进而通过改进TOPSIS法,实现对需求方的综合评价,为提供方的选择决策提供参考。文末以实例对选择方法的有效性进行了验证。该方法思路清晰,可以较好地解决云制造环境下机床资源租赁提供方企业对需求方的选择问题,具有较强的实用价值。

