基于多孔跃迁模型的流体阻力压降特性研究
刘洋,赵立新,周龙大,季豪
(1.东北石油大学机械科学与工程学院,黑龙江大庆 163318;2.黑龙江省石油石化多相介质处理及污染防治重点实验室,黑龙江大庆 163318)
0 前言
多孔介质作为流体渗流运移的载体,是自然界中广泛存在的一种具有相互联系的孔隙介质材料。从小型芯片材料到大型望远镜面板等,多孔介质的相关理论模型被广泛应用于各个领域。BASTIAN将多孔介质定义为由持续存在的固体部分和相互连通的孔隙组成的区域。孔隙中可以填充一种或多种流体,如油、水和气体等;固相可以是石英砂、玻璃珠、硅藻土等非固结的填充颗粒集合体,也可以是相互连接的柔性或刚性骨架结构。
国内外研究者利用实验测试和数值模拟方法,对非固结型填充床多孔介质中的流体流动阻力特性开展深入分析讨论并取得一定的研究成果,而对固结型多孔介质区域内的阻力压降和阻力系数的相关性研究较少。由于多孔介质复杂的内部结构,很难通过解析方法推导出阻力公式,因此,将多孔介质假设为一种虚拟的、均匀的连续介质,不同流速下的流体分子间以相互碰撞的形式实现动量交换,简化流体在多孔介质内的流动问题。多孔介质中流体流动的压降主要由黏性力和惯性力两部分组成;低雷诺数时的惯性力影响可以忽略不计,而高雷诺数时的惯性力影响显著。惯性力扭曲了流线,从而增加了速度梯度,导致压降增加。当速度增加时,流动进入非线性层流状态,此时多孔介质惯性效应不再可以忽略。
本文作者基于对多孔介质区域阻力压降方程的分析,研究固结型金属滤网内流体的阻力压降特性。设计一种用于测量求解多孔介质区域内流体阻力系数的实验装置,得到不同孔径条件下流体通过铜网的阻力压降和流速的实验值。基于对实验数据运用二项式插值非线性拟合得到的阻力系数,采用多孔跃迁模型数值模拟多孔介质区域的阻力压降特征,得到特定流速条件下的阻力压降模拟值;比较分析阻力压降的实验值和模拟值,验证了多孔介质阻力系数测定装置和方法的准确性和便捷性;对铜网区域内流场的速度场、压力场特性进行分析,验证多孔跃迁模型的适用性和准确性,为研究多孔介质区域内流体流动的阻力压降特性提供了实验测量和数值模拟的新途径。
1 阻力压降模型方程
1.1 阻力源项组成
计算流体力学的控制方程通常由非稳态项、对流项、扩散项、源项组成,如式(1)所示
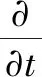
(1)
其中,连续性方程、动量方程和能量方程的各系数变量如表1所示。其中:非稳态项是由于时间的改变引起的变化;对流项是由于速度的改变引起的变化,即空间的一阶导数引起的;扩散项则是由空间的二阶导数引起的变化;而源项是发生在体积上的变化。

表1 控制方程的系数变量组成
多孔介质模型是计算流体动力学中一种常用的阻力介质模型,通常更多关注的是多孔介质区域对流体流动的影响。相对于标准流体流动方程,对于简单多孔介质模型的建模,通过增加动量源项,实现将流体在区域中受到的阻力转化为一种附加的分散阻力,将多孔介质区域简化为增加了阻力源项的流体区域,利用多孔介质模型模拟流体流动在多孔介质区域内对动量方程的影响,如式(2)所示,动量源项作用于流体产生压力梯度。
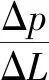
(2)
当在直角坐标系下时,动量源项表达式为
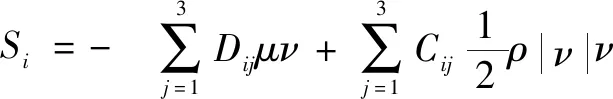
(3)
式中:Δ为多孔介质区域长度;为、、三个矢量方向的动量源项;和为系数矩阵。
当在柱坐标系下时,动量源项可以表示为
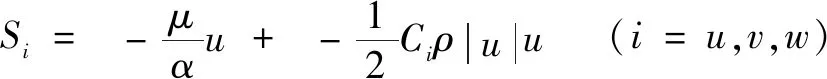
(4)
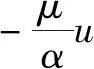
1.2 阻力压降方程
多孔介质区域内流体流动过程中,跨层压力梯度是系统几何形状、床层孔隙度、床层渗透率和流体物性的函数。DARCY(1956)基于在砂床上的体积流量和压力差所进行的实验测试,提出了一个估算体积流量的经验方程,描述流体在多孔介质中的流量、黏度和压力变化之间的比例关系。各向同性介质的达西定律表示为
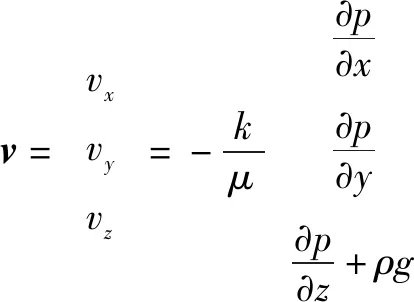
(5)
对于各向异性的介质,达西定律可以表示为
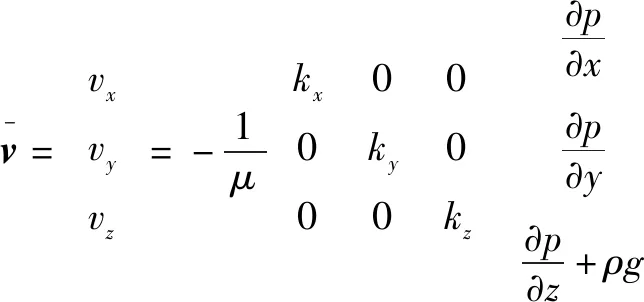
(6)
在达西模型中,流体压降与多孔介质中流体速度呈线性相关关系。已有多项研究证实并完善了多孔介质中流动的达西定律,并通过实验发现,阻力压降与流体速度的二次项有关。通常用Forchheimer方程来表示为
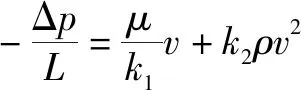
(7)
其中:Δ表示压降,Pa;表示流动方向介质长度,m;表示流体密度,kg/m;表示流体动力黏度系数,kg/(m·s);表示流体速度,m/s。通常将和分别称为达西渗透系数和非达西渗透系数。为了描述多孔介质中的非线性流动,DUPUIT(1863)和FORCHHEIMER(1901)引入了具有、系数的二次项方程来描述流动方程。
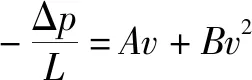
(8)
Forchheimer方程是通过实验获得的经验方程,仅给出了非线性方程的基本形式,而没有讨论方程中参数和的物理意义和影响因素,因此参数和仅能通过流体阻力的实验数据获得。
ERGUN(1952)结合Blake-Kozeny层流方程和Burke-Plummer湍流方程提出了如式(9)所示的Ergun方程,从流体速度、流体性质、孔隙率、流动方向、颗粒尺寸、颗粒形状、颗粒状固体表面等方面对该方程进行了检验。方程所适用的雷诺数范围为0.4~10。
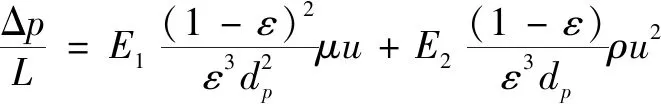
(9)
Ergun方程有效地解释了同时发生的惯性和黏性能量损失,已获得了各种颗粒形状的大量压降-流速数据的相关性。然而,有学者认为Ergun系数=150和=1.75不是常数,而是取决于雷诺数、孔隙度或颗粒形状。因此,在研究多孔介质的流动特性时,需要对Ergun关系系数进行修正,以使其适用于不同系统,通常采用拟合阻力压降和速度的实验值方法获得Ergun方程系数。
1.3 过滤阻力模型
如图1所示,根据直角坐标系下达西定律和流体体积流量和过滤截面的关系式,建立直角坐标系下水平管段内流体过滤过程的数学模型:
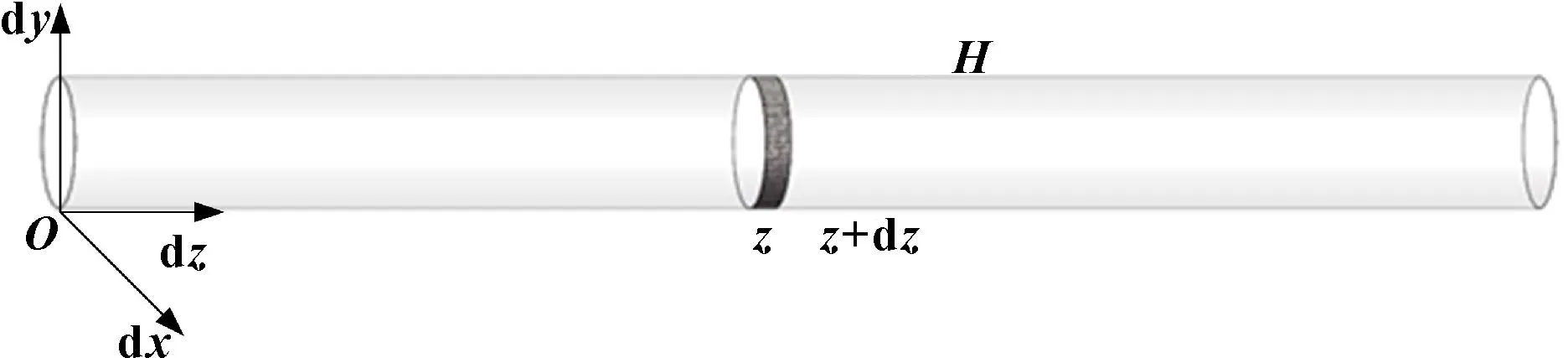
图1 直角坐标系下过滤介质内流体流动阻力模型
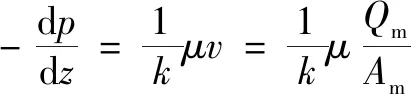
(10)
当过滤截面为圆形或椭圆形时,利用微元法选取长半轴和短半轴的微元半径分别为d和d,则过滤截面面积表达式为
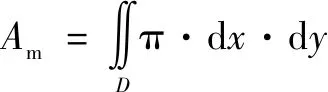
(11)
当长轴和短轴半径分别为和时,将和分别关于取值范围[0,]和[0,]积分,得到过滤截面面积表达式:
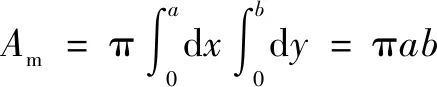
(12)
在处取厚度为d的薄层流体,过滤介质厚度(=0)=,(=)=0,过滤介质的阻力可表示为
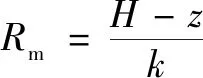
(13)
将过滤截面积和过滤阻力代入达西公式,可以得到当流体通过的过滤介质厚度为时,流体在多孔介质区域内过滤产生的过滤阻力表示为
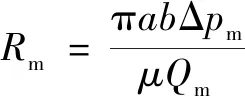
(14)
因此,流体在水平管段多孔介质区域内流动时,流动阻力与流体的体积流量成反比,与流体在多孔介质区域内产生的阻力压降Δ成正比,此外,流体动力黏度系数越大,流动阻力越小,流动区域内截面尺寸越大,流体所受到的流动阻力越大。
1.4 阻力系数求解
在多孔介质模拟区域复杂性以及流体物理特性的综合影响下,根据Buckingham提出的π定理法,假定阻力系数与液体动力黏度、液体密度、流量、孔隙率、孔隙大小、多孔介质区域水力直径、多孔介质区域单位长度的压降等有关。流体流动各参数间存在的关系为
(,,,,,,,Δ)=0
(15)
从上述8个物理量中选取3个基本变量:密度,流速,孔隙大小,根据π定理和量纲和谐原理,得到量纲为一关系方程:
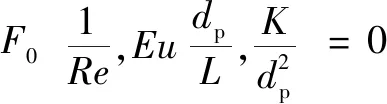
(16)
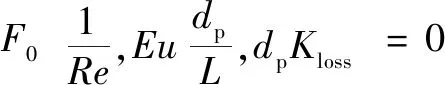
(17)
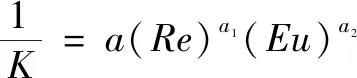
(18)
=()()
(19)
其中:、为无量纲量;、、、为待定系数。因此,多孔介质的黏性阻力系数和惯性阻力系数模型与雷诺数和欧拉数相关,可根据实验数据回归得到量纲为一的量和待定系数。
准确的阻力系数对多孔介质模拟的设置至关重要。对于Ergun方程而言,通常采用公式法和二项式拟合法计算流体在多孔介质区域内的阻力系数。其中,公式法具体为利用Ergun方程计算得到阻力系数的解析解,如式(9)和式(20);在没有相关实验数据的情况下,可以根据这些公式计算多孔介质的阻力系数,如式(21)和式(22)所示,分析流体流动的阻力特性。
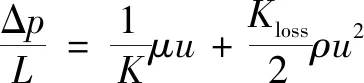
(20)
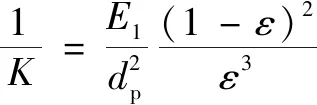
(21)
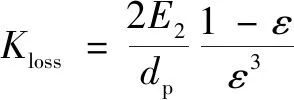
(22)
二项式拟合法具体为利用流体在多孔介质区域内的多组流速和压降实验值,根据流体流动截面面积将流量转换为表观速度,根据实验测量的多孔介质在流动方向上的长度将压降转换为压力梯度,进行二项式插值拟合,得到拟合常数和,再计算出阻力系数。
Δ=+
(23)
如果在数值模拟前已开展实验研究,利用对压力降与流体流速的实验数据进行二项式插值拟合的方法可确定以黏性阻力系数和惯性阻力系数为待求解参数,以流体在试验管段内的流速为自变量,流体在试验管段两端所产生的压力降值Δ为函数对阻力系数进行多项式拟合。
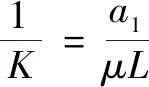
(24)
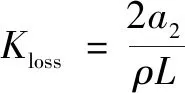
(25)
2 阻力压降测量系统实验
2.1 实验原理和方法
阻力压降实验采用80目、120目、150目和200目的黄铜网作为固结型多孔介质区域,多孔介质的孔隙率被定义为孔隙体积与总体积的比值。图2所示为黄铜网结构单元尺寸,滤网的目数与滤网丝径和孔径有关,根据假设所选黄铜网为丝径和孔径为均匀滤网的结构特点,滤网的孔隙率可由式(28)计算得到,各尺寸铜网孔隙率如表2所示。

图2 滤网结构单元尺寸图
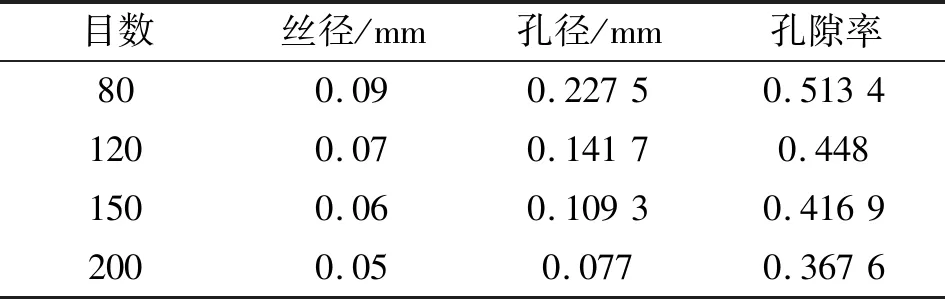
表2 铜网尺寸参数和孔隙率
单位滤网的表面积和体积分别为式(26)和(27)所示
=π
(26)
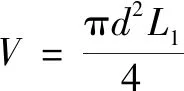
(27)
其中:为单根金属丝的直径,又称滤网厚度,m;为滤网单元的边长,又称滤网孔径,m。滤网的目数可表示为在25.4 mm长度上排列着个孔隙,则该滤网为目,由此可知,滤网孔隙率为
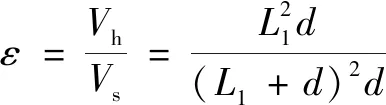
(28)
其中:为整个滤网的孔隙体积,m;为整个滤网的体积,m。
根据固结型和非固结型多孔介质材料的结构特点,设计一种用于流体通过不同类型多孔介质时,测量计算阻力系数的实验装置,如图3所示。该装置特点在于可以测量固结型的金属泡沫、滤网等,也可以测量非固结型填充床的阻力系数。
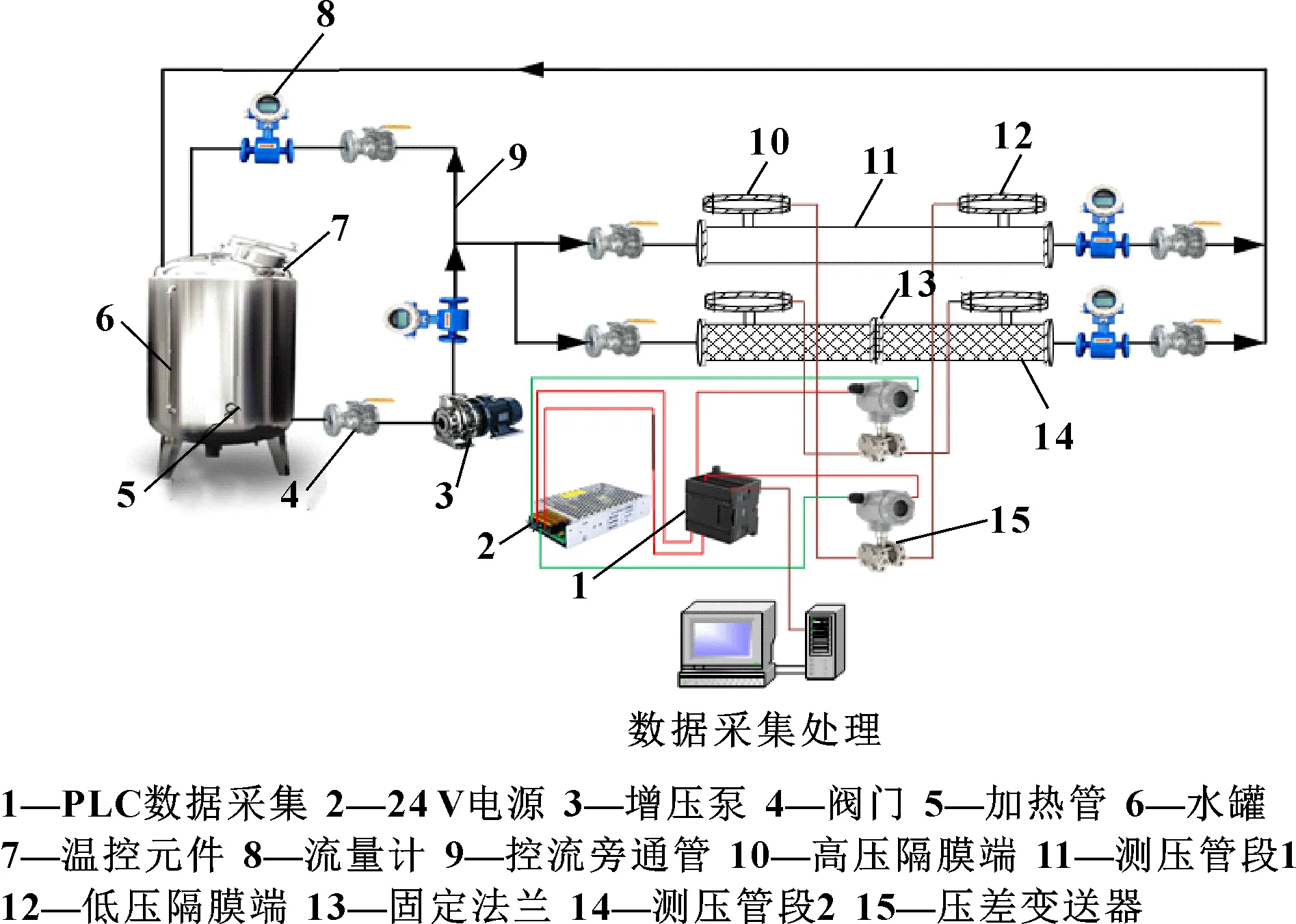
图3 多孔介质阻力系数测量装置
该装置由储液系统、动力系统、监测系统、数据采集处理系统、测量管段系统等组成,选取金属铜滤网作为固结型多孔介质材料进行实验。水罐内安装有加热管和温控热电偶元件,实现对罐内液体的控温调节。测量管段系统由材质、尺寸完全相同的测压管段1和测压管段2组成,管段2内通过填充颗粒和法兰固定滤网的方式构建不同结构多孔介质区域。如图4所示,两组测量管段分别安装连接压差变送器的高压隔膜端和低压隔膜端,实现混合液通过管段1时产生的管段阻力压降损失和混合液通过管段2内多孔介质区域时产生的阻力压降损失的测量。

图4 压差变送器测压端隔膜法兰式连接装置
根据流量计测得管段1、2内通过的体积流量和,可得到相应流速分别为和;根据压降-流速的相关性对测量管段1所得的压降损失和流速采用插值法进行二项式拟合,得到式(23)中拟合系数和;再将由测量管段2所得的流速代入拟合关系式,可得到管段1与管段2在相同流速条件下所产生的阻力压降损失,因此,流体通过管段2内多孔介质区域时产生的阻力压降损失为
Δ=-
(29)
将测压管段2的压降和流速实验值代入式(20)中,拟合得到管段2内的相关阻力系数。
2.2 实验结果及分析
20 ℃水分别通过80目、120目、150目、200目铜网时,得到的流速和压降的实验值如图5所示。测量铜网压降均随入口速度的增大而增大,入口速度较小时,阻力压降变化幅度较小,随入口速度的增大,阻力压降变化幅度逐渐增大。由孔隙率测量计算可知,随着铜网从80目增大至200目,单位长度上的孔隙增多,单位孔径尺寸减小,孔隙率减小;相同速度条件下,滤网压降随着目数的增加而增大。利用不同孔径铜网的压降和速度实验值得到的阻力系数拟合结果列于表3中。随着铜网目数的增大,黏性阻力系数和惯性阻力系数均逐渐增大,由相关指数分别为99.823%、99.533%、99.356%、99.674%,说明压降变化的差异中大于99%都是由速度变化引起的,方程拟合较好。
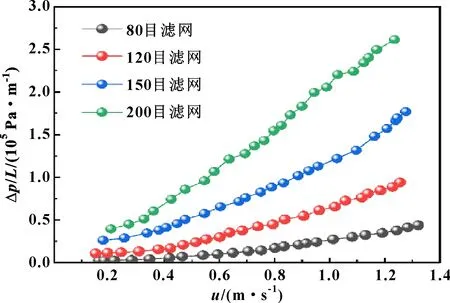
图5 20 ℃水通过不同规格滤网阻力压降变化
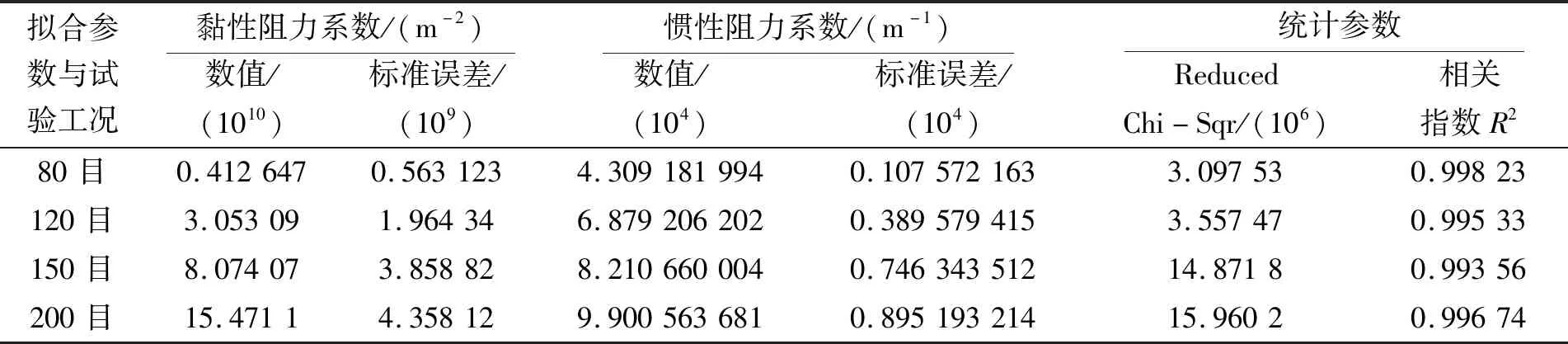
表3 黏性阻力系数和惯性阻力系数二项式插值非线性拟合结果
当单位长度铜网的孔隙数增大时,孔径尺寸减小,孔隙率降低。流体通过滤网所受到的阻力增大,流体的渗透性降低。根据达西定律可知,流体的黏性阻力系数与渗透率成反比,因此,随着滤网孔隙数的增大,黏性阻力系数增大。由于孔隙变化使得流体流动截面缩小,在滤网内产生速度梯度,加速运动的流体引起附加阻力,同时引起流体动能变化,附加阻力与加速度成正比,阻力系数即为惯性阻力系数,随着铜网目数的增大,惯性阻力系数增大。
3 多孔跃迁模型数值模拟
通过对多孔介质模型中黏性阻力系数和惯性阻力系数的设置,模拟流体通过金属滤网为多孔介质材料时的阻力压降变化情况。阻力系数的准确性和多孔跃迁模型的有效性,都对数值模拟的计算结果产生较大的影响,通过设定实验测量数据拟合得到阻力系数,模拟计算阻力压降值,比较实验值和模拟值,验证多孔跃迁模型的可行性。
3.1 几何模型和网格划分
利用SolidWorks建模软件建立圆管几何模型,其中直径为25 mm,长度为700 mm;利用ICEM CFD划分结构网格,如图6所示。
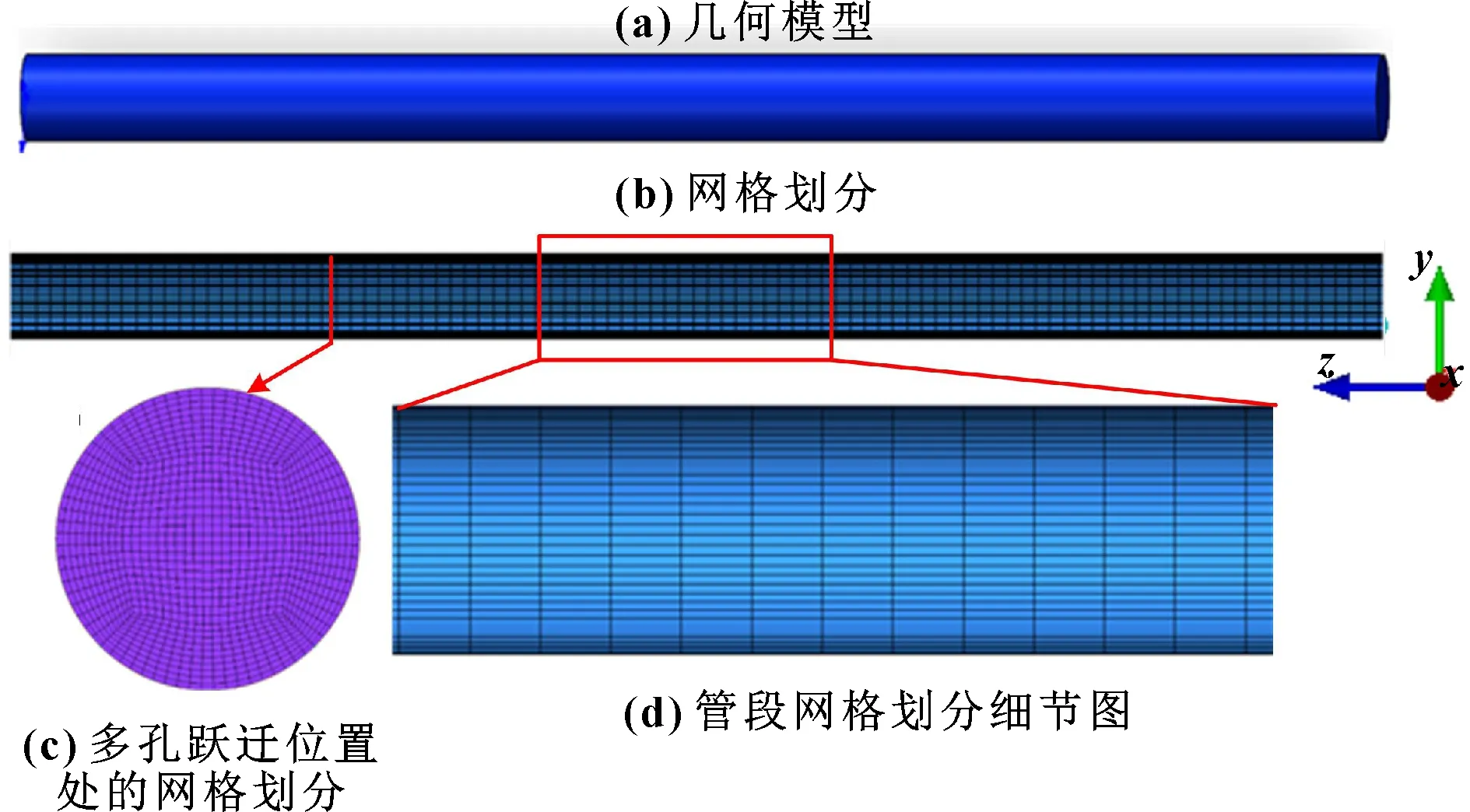
图6 几何模型和网格划分
3.2 模拟条件和工况
多孔跃迁模型被用来模拟一个具有已知速度或压降特性的面区域,而不是单元区域,本质上是对结构区域的多孔介质模型的一维简化。多孔跃迁模型与完整的多孔介质模型相比更稳健,能产生更好的收敛效果。
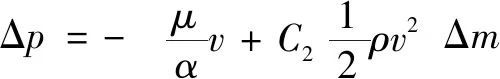
(30)
其中:是层流流体的黏度;是介质表面的渗透率;是压力-跃迁系数;是多孔面的法线速度;Δ是介质的厚度。当多孔跃迁是将两个流体区分开,或在一个流体区形成一个内部区域时,多孔跃迁定义的厚度和系数参数被用来计算跨越跃迁的压力降,这个压降被转换为一个不包含黏性力的力矢量。
多孔跃迁模型需要设置多孔介质面区域的表面渗透率、多孔介质的有限厚度、压力跃迁系数,其中,表面渗透率与黏性阻力系数成倒数关系,压力跃迁系数等于惯性阻力系数,介质厚度为丝径大小,具体流体及工况参数详见表4。求解器采用压力基耦合绝对速度Simple算法,二阶迎风离散格式,稳态单相流。采用Realizable-湍流模型,考虑流场的旋转以及弯曲壁面流动,边界条件采用速度入口,压力出口,出口压力=0,壁面无滑移,残差收敛设置为10×10。

表4 流体及工况参数
3.3 网格无关性检验
数值模拟过程中,几何模型的网格划分精度决定了计算过程的精确性和准确度。通常划分的网格数量越多,计算结果的精度越高,但是往往受限于计算过程的时间成本和计算设备的硬件条件限制,网格划分的方法、数量影响着模拟方法的选择。如表5所示,分别以18 795、38 520、54 912、72 225四种网格划分数量为对象,讨论当入口速度为0.65、0.7、0.75 m/s时的阻力压降,如图7所示。不同速度条件下,阻力压降均呈现出先升高后降低至稳定波动,确定选取网格数量为54 912开展数值模拟分析。

表5 几何结构网格无关性检验参数
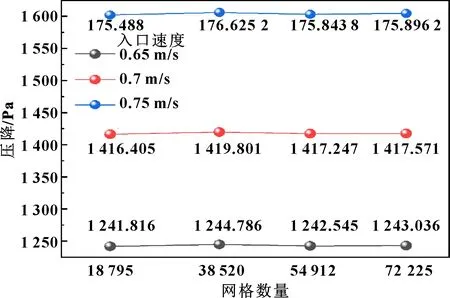
图7 网格独立性检验过程
3.4 结果分析和讨论
图8所示为200目铜网在不同入口速度0.2、0.6、1.0、1.4 m/s条件下的截面的阻力压降云图。结合几何模型结构,由于在距离入口0.2 m处设置为多孔跃迁层,可以看出在圆管区域内阻力压降发生明显降低趋势,随着入口速度的增加,区域内的阻力压降为1 672.135、5 709.251、10 623.79、16 417.1 Pa,呈逐渐增大趋势。
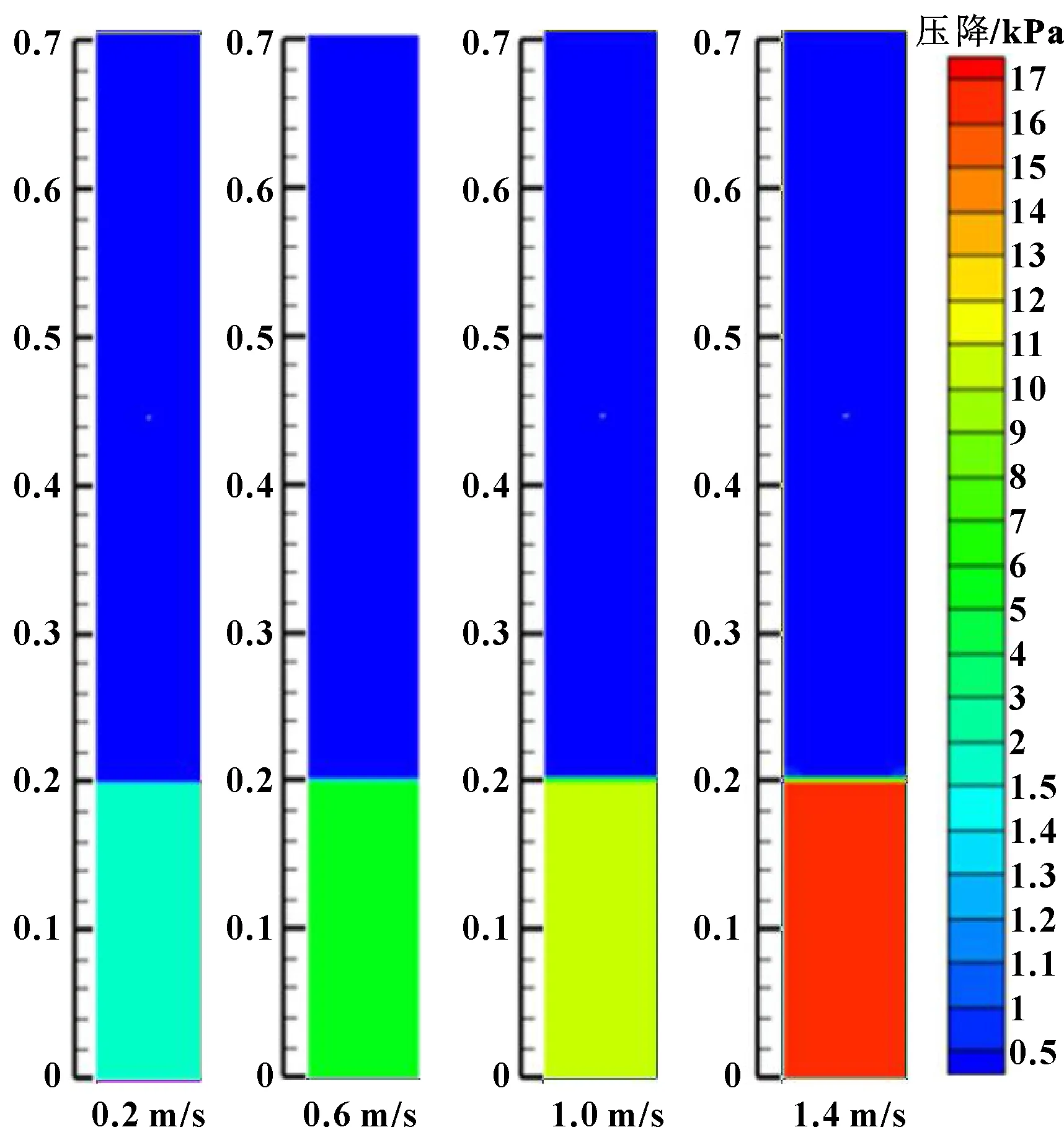
图8 200目时不同流速下yoz截面压降云图
如图9所示,不同尺寸铜网的阻力压降实验值和模拟值比较,其中,图9(a)(b)(c)(d)分别显示了实验值和模拟值间标准差的误差线情况。可以看出:当入口速度较低时,误差线较小;随着入口速度的增大,误差线有逐渐增大趋势。说明随着速度的增大,阻力压降与流体速度间逐渐偏离达西公式的线性关系。
图9(e)(f)(g)(h)分别显示了当置信水平为95%时,阻力压降的实验值和模拟值的置信区间拟合线,实验值和拟合值的预测关系为1∶1。线性拟合得到的比例关系分别为1.168 64、1.106 21、1.083 27、0.853 18,得到的相关指数分别为99.821%、99.592%、99.474%、99.65%,说明线性拟合效果较好,阻力压降的实验值和模拟值吻合较好,通过实验值求解的黏性阻力系数和惯性阻力系数具有较高的准确性,所设计的阻力系数测量装置具有较好的适用性,同时所采用的多孔跃迁模型能够准确模拟阻力压降的变化情况,体现出较好的运算精度和收敛性。
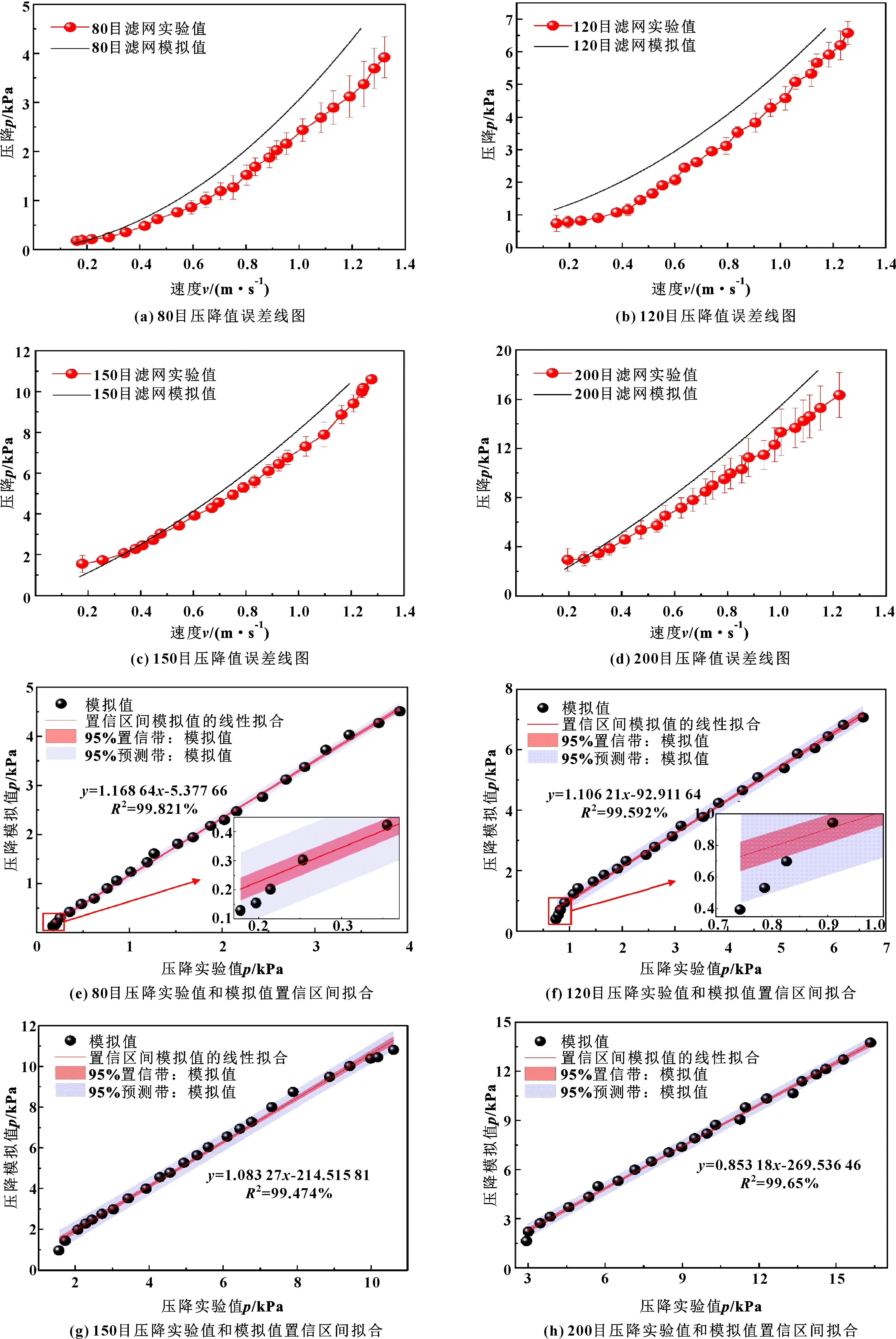
图9 不同尺寸铜网的阻力压降实验值和模拟值比较
图10所示为速度沿流体域的轴心线分布情况,可以看出:速度在流动方向上距离入口0.2 m附近先发生大幅度下降。结合几何模型结构,此位置为多孔跃迁区域,分别设置为不同孔径规格的80目、120目、150目和200目铜网,通过局部放大图可以明显看出初始入口速度越大,铜网附近速度下降幅度越大,在通过铜网孔隙的过程中流通截面减小,流出铜网后会产生流速增大的趋势,所产生的阻力压降一部分用来克服黏性阻力和惯性阻力,另一部分转化为流体通过铜网后的动能,且初始入口速度越大,所产生的速度梯度越大,符合阻力压降与流体速度的变化规律。
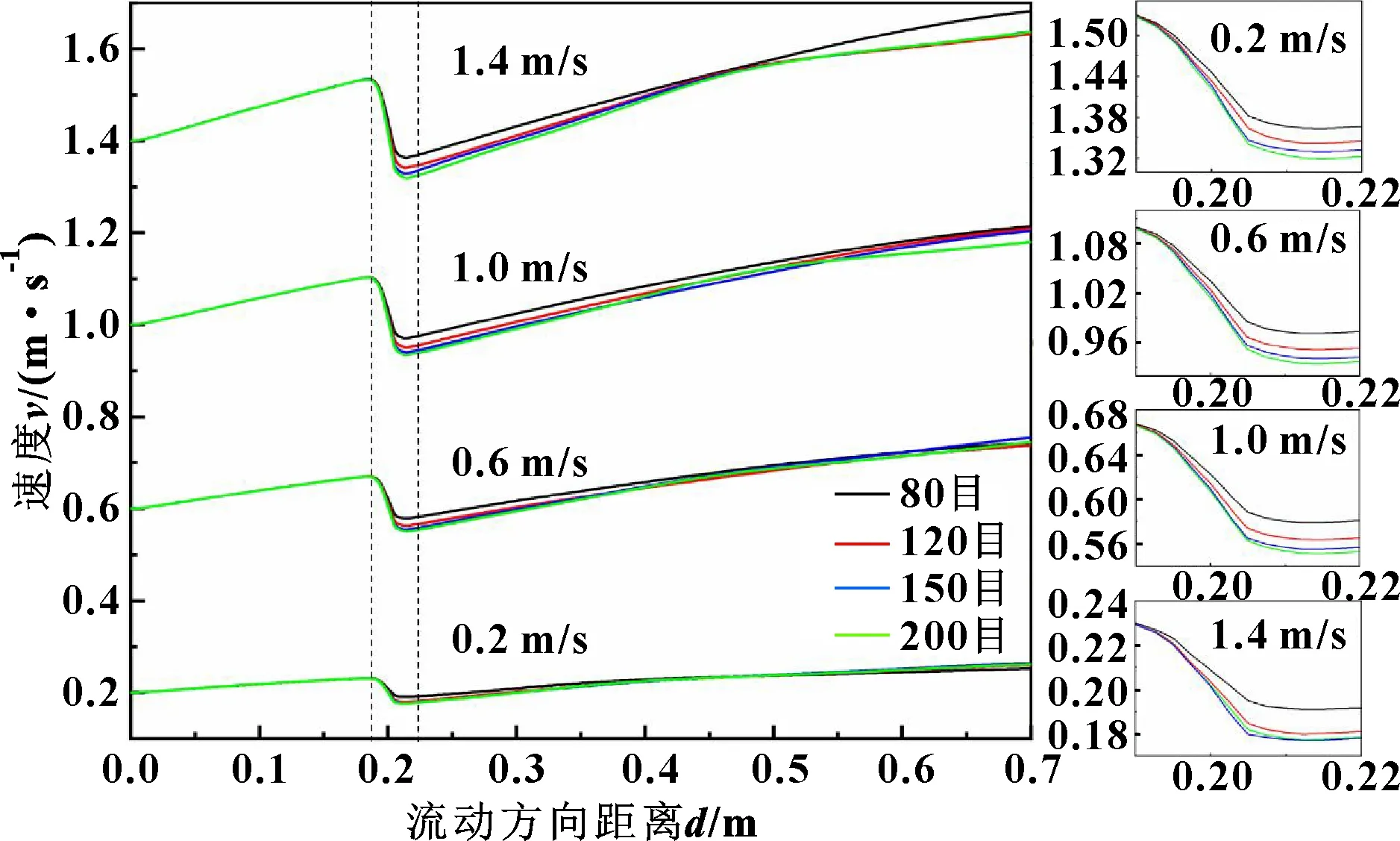
图10 不同尺寸铜网在流动方向的轴心线上速度变化曲线
如图11所示,分别显示200目铜网作为数值模拟多孔跃迁区域,入口速度为0.2、0.6、1.0、1.4 m/s时,沿流动方向截面上的速度场变化云图。可以看出:在距离入口0.2 m处速度场梯度波动明显。结合前述流动方向轴心线上速度变化分析,各速度场云图的梯度变化趋势基本一致,在0.2 m处为多孔跃迁模型位置,速度场从入口处先增大至多孔跃迁区域,在多孔跃迁区域内产生阻力压降,之后速度场先短暂减小,经过多孔跃迁稳定区域后,流体速度场逐渐增大直至流动区域出口,而由轴心至壁面处的速度场呈梯度降低趋势。
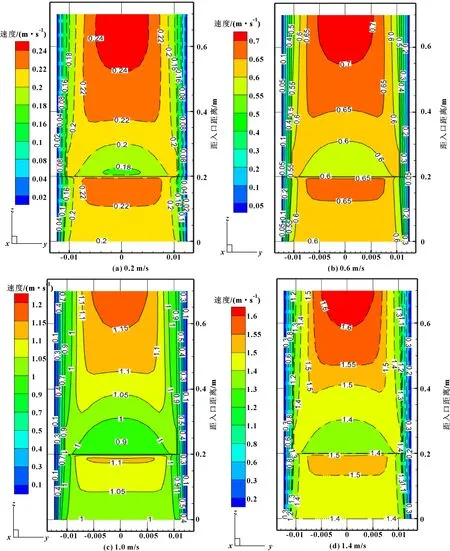
图11 不同流速下200目铜网yoz截面速度云图
4 结论
(1)流体在水平管段多孔介质区域内的流动阻力与流体的体积流量成反比,与流体在多孔介质区域内产生的阻力压降Δ成正比。流体动力黏度系数越大,流动阻力越小,流动区域内截面尺寸越大,流体所受到的流动阻力越大。
(2) 利用无量纲π定理分析法,多孔介质的黏性阻力系数和惯性阻力系数模型与雷诺数和欧拉数相关,根据实验值回归得到量纲为一的量和待定系数。
(3)随着铜网从80目增大至200目,单位长度上的孔隙增多,单位孔径尺寸减小,孔隙率减小。铜网阻力压降均随入口速度的增大而增大,入口速度较小时,阻力压降变化幅度较小,随入口速度的增大,阻力压降变化幅度逐渐增大;相同速度条件下,铜网阻力压降随着目数的增加而增大。
(4)通过铜网内流体阻力系数测量装置得到的不同孔径条件下阻力压降实验值,与利用多孔跃迁模型得到的模拟值吻合较好。多孔跃迁模型区域内产生的阻力压降部分用来克服黏性阻力和惯性阻力,部分用来转化为影响流体通过多孔跃迁区域后速度场逐渐增加的动能。

