例谈2021年全国数学高考乙卷第21题（2）突破方法

甘肃省永昌县第一高级中学 赵忠平 737200

2021 年高考全国数学I(乙)卷命题聚焦核心素养，突出关键能力考查，科学把握必备知识与关键能力的关联，稳中求新，满足了基础性、综合性、应用性和创新性的考查要求.其中第21 题为全卷的压轴题，命题角度新，突破口宽，但深入解答难，很好的考查了学生数学抽象、逻辑推理、数学建模、数学运算等方面的数学素养.笔者谈谈这道题目的解题突破方法，以及解析几何教学的备考策略，供参考.

1 高考试题及突破方法分析

题目：已知抛物线C:x2=2py()p＞0 的焦点为F，且F与圆M:x2+(y+4)2=1 上的点的距离的最小值为4.(1)求p；（2）若点P在圆M上，PA、PB是C的两条切线，A、B是切点，求△PAB面积的最大值.

本题第（1）问易求p=2;第（2）问可以从多个角度切入，下面具体分析：

点评:求面积的最值问题一般转化为弦长问题处理，所以设直线AB方程，与抛物线方程联立方程组，结合根与系数关系及弦长公式求出底边长，再利用点到直线距离公式求出高，从而得到面积表达式，利用函数单调性求最值.

点评：本解法选择以切线方程为切入点，运用判别式表征相切关系，利用减元思想及整体代换，实现问题的求解.

策略3：设出A(x1,y1)、B(x2,y2)，利用导数方法表示出切线斜率，进一步写出两条切线方程，利用同构方程得到切点弦方程.

点评：本解法选择以坐标为切入点的策略，从导数的视角研究切点，推导出切点弦方程，进一步求出弦长和P到直线AB的距离，表示出面积再利用函数单调性求最值.此处也可以推导出抛物线切点弦方程的一般形式，即过P(x0,y0)做抛物线x2=2py(p＞0)的两条切线PA、PB，切点为A、B，则直线AB方程为x0x=p(y0+y)，如果直接利用这个结论则更容易求解.

策略4：以设点A、B的坐标为切入点，得到AB的中点N的坐标和两条切线PA、PB交 点P的坐标，发现PN∥y轴，把△PAB分割成两个三角形求面积的和.

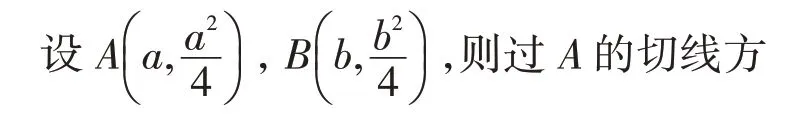
点评：在求图形面积时将图形分割成若干小的图形求面积之和是常见解题策略，本题在求解过程中发现PN∥y轴，从而将△PAB分割成两个三角形求其面积之和，实现问题的巧妙转化.

2 备考策略

2.1 重视学生数学多元表征能力和数学抽象能力的培养

解析几何教学中要教会学生“先用几何眼光观察，再用坐标法推理、论证和求解”的基本思路，不要忽视“几何要素的分析”这一环[1].在解析几何解题教学中，引导学生对同一个条件，从不同角度、利用不同语言进行表征，比较表征结果的优劣，在解题教学中要对不同的表征方法做出示范，引导学生体会不同表征方式对于解题过程的具体影响，从中选择最优表征方法.例如对于曲线的切线问题有代数法、几何法、导数法等多种表征方法.

2.2 重视解析几何中学生运算素养的培养

解析几何试题对学生运算能力要求很高，因此解析几何教学中要把握解析几何运算的特点，低起点、缓坡度、有预见性地指导学生进行解析几何运算，让学生体会、感悟、总结解析几何运算技巧.另外，解析几何教学中，提高运算能力不能仅仅要从代数角度入手，还要努力提高学生的几何图形分析能力，要在落实数形结合思想上下功夫[1].

2.3 重视解析几何与其他知识交汇点的教学

高考试题突出以“一核四层四翼”的高考评价标准，突出以知识立意、能力立意向素养立意的转变，因此在解析几何教学中要重视知识交汇点的教学，引导学生对交汇问题进行深度体验、发散思考、拓展延伸，使学生在自主体验中积累经验、学会思考、提升素养.