应用斯特温面积法证明两线段相等

江苏省泰州市海陵区森南新村15栋103室 于志洪 225300

1973 年，美国中学老师斯特温（Steuen）应用面积方法对著名的“蝴蝶定理”进行了简捷明了的证明，后来人们就将这种证明方法称之为“斯特温面积法”.下面就介绍如何运用“斯特温面积法”来证明两线段的相等.

例1 已知过圆的弦AB的中点M，任意引两弦CD和EF，连接DE与CF，分别交AB于P、Q.求证：MP=MQ.（蝴蝶定理）（第24届美国大学生数学竞赛题）

图1

例2 过正方形ABCD的顶点D作DF//AC，且CF=AC,CF与AD的延长线交于M.求证：AM=AF.（2010 年沙市高中数学竞赛题）

图2

例3 设P、Q为线段BC上两定点，且BP=CQ.A为BC外的一点，当点A运动到使∠BAP=∠CAQ时，求证：△ABC是等腰三角形.（1986年全国初中数学竞赛题）

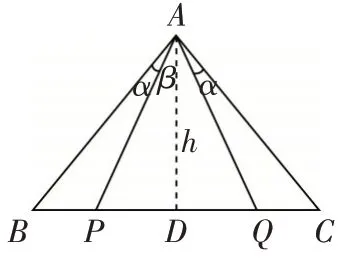
图3

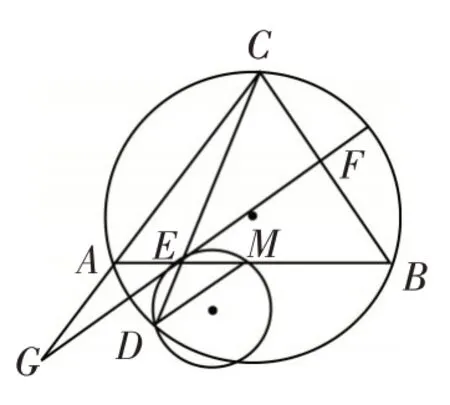
图4

综上所述，应用斯特温面积法证明两线段相等，首先观察图形，根据题设，建立斯特温面积等式；然后利用三角形的边角与面积之间的关系，结合“等高的三角形面积的比等于底边的比”和“等底的三角形面积的比等于高的比”的性质，将有关关系式代入斯特温面积等式，通过化简运算进行证明即可.用斯特温面积法证几何题，不添加任何辅助线，现将这种思维方法归纳如下：

依据题中结论与条件的关系，确定几个相关的三角形，其面积依次为S1、S2、S3…、Sn，组成比积式.再把需要的面积公式代入计算或化简，从而使问题获得解决.此法富有规律，方法明晰，符合新课程改革的理念要求，利于学生融会贯通所学几何和代数知识，对予培养学生学习数学的兴趣、提高教学质量均颇有益处.加强这一专题内容的研究，很有必要.